机器学习复习(8)——逻辑回归
目录
逻辑函数(Logistic Function)
逻辑回归模型的假设函数
从逻辑回归模型转换到最大似然函数过程
最大似然函数方法
梯度下降
逻辑函数(Logistic Function)
首先,逻辑函数,也称为Sigmoid函数,是一个常见的S形函数。其数学表达式为:
这个函数的特点是,其输出值总是在0和1之间。这个性质使得Sigmoid函数非常适合用来进行二分类,在机器学习中,它可以将任意实数映射到(0, 1)区间,用来表示某个事件发生的概率。例如,在逻辑回归模型中,我们可以用它来预测一个实例属于某个类别的概率。
def sigmoid(z):return 1 / (1 + np.exp(-z))可视化:
nums = np.arange(-10, 10, step=1)fig, ax = plt.subplots(figsize=(12,8))
ax.plot(nums, sigmoid(nums), 'r')
plt.show()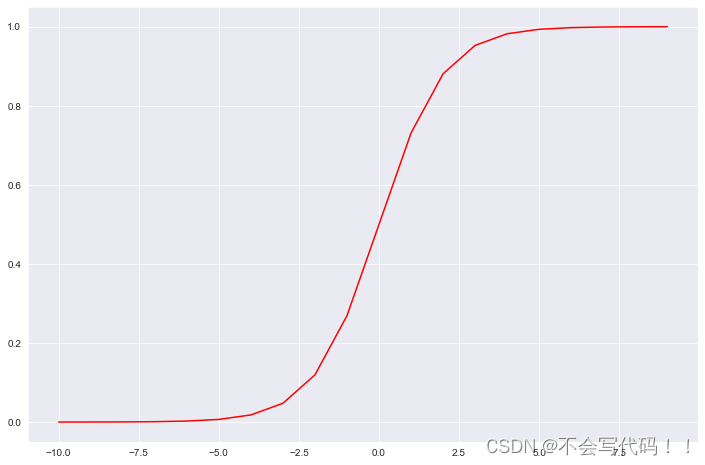
逻辑回归模型的假设函数
逻辑回归模型的假设函数将输入特征X和参数θ的线性组合通过逻辑函数转换为一个概率值,其公式为:

这里,θ^T X是参数θ和输入特征X的点积,它将多个输入特征线性组合成一个实数值,然后通过逻辑函数映射到(0, 1)区间。这个映射的结果可以被解释为在给定输入特征X的条件下,预测结果为正类的概率。
逻辑回归模型通过优化参数θ来最大化观测数据的似然函数,从而找到最佳的决策边界,以区分不同的类别。在实际应用中,逻辑回归是一个非常强大且广泛使用的分类算法,特别是在二分类问题中。
从逻辑回归模型转换到最大似然函数过程
逻辑回归模型的假设函数定义为:
为了找到最佳的参数θ,我们使用最大似然估计。对于二分类问题,给定的数据集,其中
,,我们可以写出似然函数:
这个似然函数表示了,在给定参数θ和输入X的条件下,观察到当前数据集y的概率。最大化这个似然函数等价于最大化观测数据在当前模型参数下出现的概率。
为了便于计算,通常对似然函数取对数,得到对数似然函数:
最大化对数似然函数相对简单,因为对数函数是单调的,且对数似然函数是关于θ的凸函数,容易通过梯度下降等优化算法找到全局最优解。
在机器学习中,我们通常通过最小化损失函数(而不是最大化似然函数)来训练模型。因此,我们将最大化对数似然问题转化为最小化损失函数问题。损失函数是对数似然函数的负值,平均化到每个样本上,即:

这就是逻辑回归中使用的损失函数,也称为对数损失或交叉熵损失。通过最小化这个损失函数,我们可以找到最佳的模型参数θ,使模型对训练数据的拟合程度最高,即最可能产生观测数据的参数。
最大似然函数方法
由于乘除法不太好优化计算,通常通过对数的方法进行优化求解,损失函数如下:

def cost(theta, X, y):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)first = np.multiply(-y, np.log(sigmoid(X * theta.T)))second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))return np.sum(first - second) / (len(X))梯度下降
实际上这里只计算量梯度,并没有下降
def gradient(theta, X, y):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)parameters = int(theta.ravel().shape[1])grad = np.zeros(parameters)error = sigmoid(X * theta.T) - yfor i in range(parameters):term = np.multiply(error, X[:,i])grad[i] = np.sum(term) / len(X)return grad相关文章:

机器学习复习(8)——逻辑回归
目录 逻辑函数(Logistic Function) 逻辑回归模型的假设函数 从逻辑回归模型转换到最大似然函数过程 最大似然函数方法 梯度下降 逻辑函数(Logistic Function) 首先,逻辑函数,也称为Sigmoid函数&#…...

深入解析MySQL 8:事务数据字典的变革
随着数据库技术的不断发展和完善,元数据的管理成为了一个日益重要的议题。在MySQL 8中,一项引人注目的新特性是引入了事务数据字典(Transaction Data Dictionary,简称TDD),它改变了元数据的管理方式&#x…...
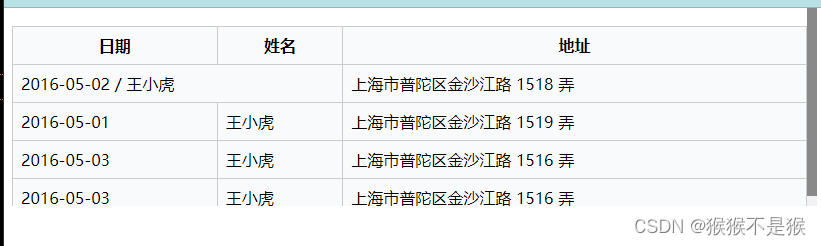
jquery写表格,通过后端传值,并合并单元格
<!DOCTYPE html> <html> <head><title>Table Using jQuery</title><style>#tableWrapper {width: 100%;height: 200px; /* 设置表格容器的高度 */overflow: auto; /* 添加滚动条 */margin-top: -10px; /* 负的外边距值,根据实际…...
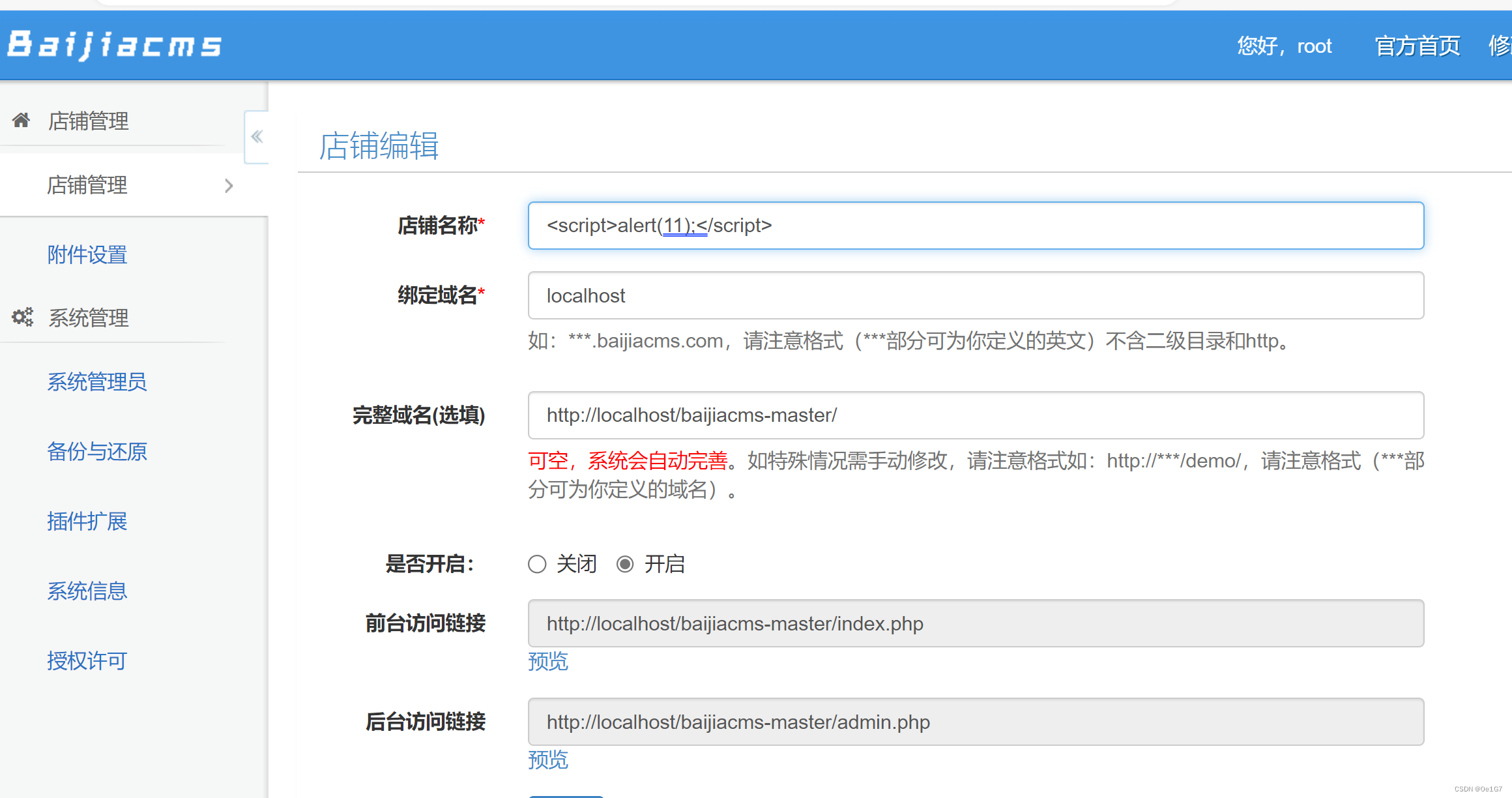
百家cms代审
参考博客: PHP代码审计之旅之百家CMS-腾讯云开发者社区-腾讯云 环境搭建 源码链接如下所示 https://gitee.com/openbaijia/baijiacms 安装至本地后 直接解压到phpstudy的www目录下即可 接下来去创建一个数据库用于存储CMS信息。(在Mysql命令行中执行…...
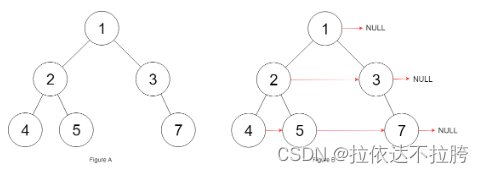
算法学习——LeetCode力扣二叉树篇3
算法学习——LeetCode力扣二叉树篇3 116. 填充每个节点的下一个右侧节点指针 116. 填充每个节点的下一个右侧节点指针 - 力扣(LeetCode) 描述 给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树…...

强制卸载挂载目录
当遇到磁盘卸载失败提示 device is busy fuser -a 显示所有命令行中指定的文件,默认情况下被访问的文件才会被显示。 -c 和-m一样,用于POSIX兼容。 -k 杀掉访问文件的进程。如果没有指定-signal就会发送SIGKILL信号。结合 –signal -signal 使用指定的信…...

HiveSQL——sum(if()) 条件累加
注:参考文章: HiveSql面试题10--sum(if)统计问题_hive sum if-CSDN博客文章浏览阅读5.8k次,点赞6次,收藏19次。0 需求分析t_order表结构字段名含义oid订单编号uid用户idotime订单时间(yyyy-MM-dd)oamount订…...

Linux命令行工具使用HTTP代理的方法详解
亲爱的Linux用户们,有没有想过在命令行世界里,你的每一个指令都能悄无声息地穿越千山万水,而不被外界窥探?哈哈,没错,就是通过HTTP代理!今天,我们就来一起探索如何在Linux命令行工具…...

idea mavn 中途新建gitignore文件如何生效
两种情况下项目代码中新建gitignore文件如何生效。 第一种情况项目代码下没有模块的情况 直接在该项目代码的根目录下进入git命令行执行: git rm -r --cached . git add . 注意上面两个命令后面都有一个点 第二种情况是有模块的情况 需要进入模块目录执行上…...
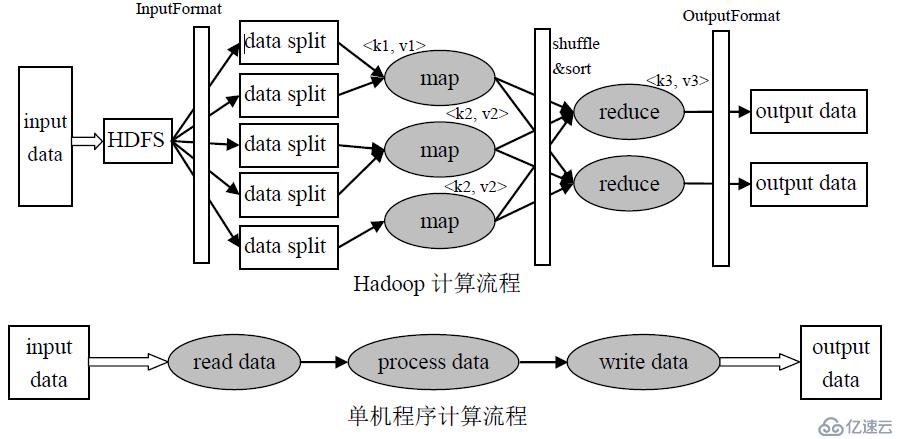
Hadoop:认识MapReduce
MapReduce是一个用于处理大数据集的编程模型和算法框架。其优势在于能够处理大量的数据,通过并行化来加速计算过程。它适用于那些可以分解为多个独立子任务的计算密集型作业,如文本处理、数据分析和大规模数据集的聚合等。然而,MapReduce也有…...

9.4 OpenGL帧缓冲:纹理和帧缓冲之间的反馈循环
纹理和帧缓冲之间的反馈循环 Feedback Loops Between Textures and the Framebuffer 当在图形编程中,特别是OpenGL这样的图形API中处理纹理(Texture)和帧缓冲区(Framebuffer)时,可能会出现一种称为“反馈循…...
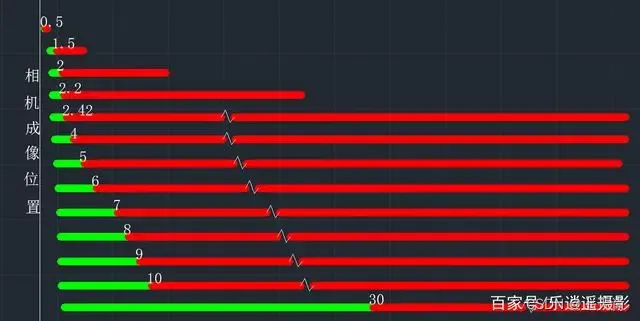
相机图像质量研究(6)常见问题总结:光学结构对成像的影响--对焦距离
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...

fast.ai 机器学习笔记(二)
机器学习 1:第 5 课 原文:medium.com/hiromi_suenaga/machine-learning-1-lesson-5-df45f0c99618 译者:飞龙 协议:CC BY-NC-SA 4.0 来自机器学习课程的个人笔记。随着我继续复习课程以“真正”理解它,这些笔记将继续更…...

vue3 elementplus DateTimePicker 日期时间设置默认时间为当天
DateTimePicker里面有个自带属性 可以实现这个需求,如图: // 设置当前当天时间范围 00: 00: 00 - 23:59:59 const currentDate [setDefaultDate(0), setDefaultDate(1)]const setDefaultDate (type:number ): string > {let t ;let date new Da…...

2024年笔记--centos docker离线安装启动失败
Failed to start Docker Application Container Engine 错误如下: [rootel70 docker]# systemctl start docker.service Job for docker.service failed because start of the service was attempted too often. See "systemctl status docker.service" …...
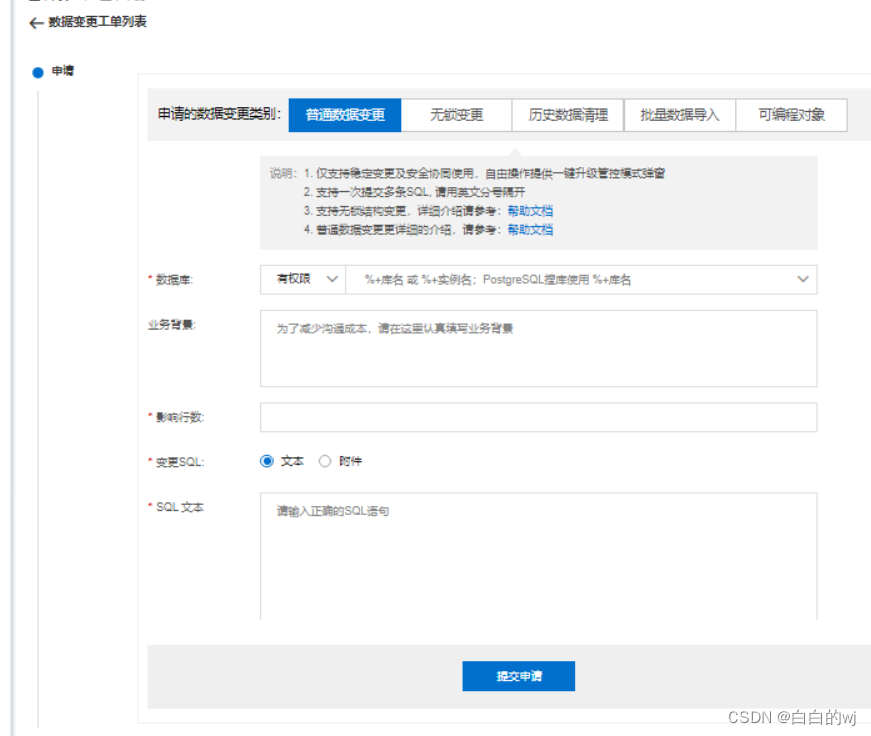
2024.2.10 DMS(数据库管理系统)初体验
数据库管理系统(Database Management System)是一种操纵和管理数据库的大型软件,用于建立、使用和维护数据库,简称DBMS。它对数据库进行统一的管理和控制,以保证数据库的安全性和完整性。用户通过DBMS访问数据库中的数据,数据库管…...

zk集群--集群同步
1.概述 前面一章分析了集群下启动阶段选举过程,一旦完成选举,通过执行QuorumPeer的setPeerState将设置好选举结束后自身的状态。然后,将再次执行QuorumPeer的run的新的一轮循环, QuorumPeer的run的每一轮循环,先判断…...

复习面经哦
1.函数可以变量提升 JavaScript 中的函数存在变量提升的概念,这意味着在执行代码之前,函数声明会被提升到其作用域的顶部。这使得你可以在函数声明之前调用函数。然而,这种行为只适用于函数声明,而不是函数表达式。 下面是一些关…...
vector)
c++ STL系列——(二)vector
引言 在现代C编程中,std::vector是最常用的动态数组实现之一,它是C标准模板库(STL)的一部分。vector提供了一种方式,以单一数据结构来存储元素集合,并且可以动态地调整大小以适应新元素。本文将深入探讨ve…...
STM32能够做到数据采集和发送同时进行吗?
STM32能够做到数据采集和发送同时进行吗? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「STM32的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!&am…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
