C#,欧拉常数(Euler Constant)的算法与源代码

1 欧拉常数
欧拉常数最先由瑞士数学家莱昂哈德· 欧拉 (Leonhard Euler) 在1735年发表的文章《De Progressionibus harmonicus observationes》中定义。欧拉曾经使用γ作为它的符号,并计算出了它的前6位,1761年他又将该值计算到了16位 。
欧拉常数最先由瑞士数学家莱昂哈德·欧拉(Leonhard Euler)在1735年发表的文章 De Progressionibus harmonicus observationes 中定义。欧拉曾经使用C作为它的符号,并计算出了它的前6位小数。1761年他又将该值计算到了16位小数。1790年,意大利数学家马歇罗尼(Lorenzo Mascheroni)引入了γ作为这个常数的符号,并将该常数计算到小数点后32位。但后来的计算显示他在第20位的时候出现了错误。欧拉数以世界著名数学家欧拉名字命名;还有一个鲜为人知的名字纳皮尔常数,用来纪念苏格兰数学家约翰·纳皮尔 (John Napier) 引进对数 。
2 计算结果
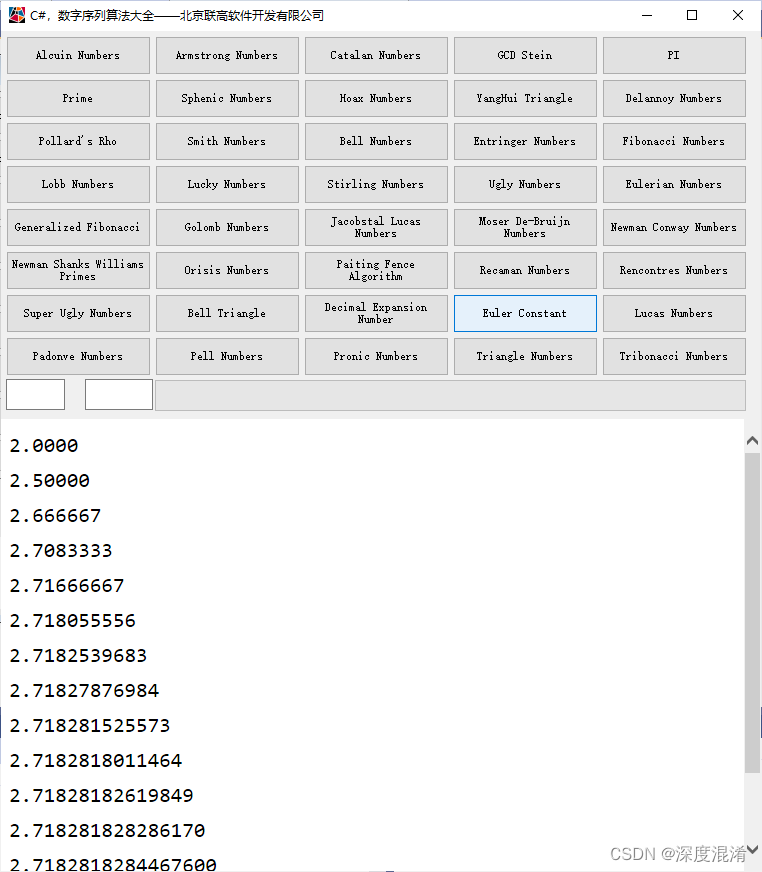
3 源程序
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
private static double doubleFactorial(int n)
{
if (n == 1) return 1;
else return n * doubleFactorial(n - 1);
}
public static double Euler_Constant(int n)
{
if (n == 0) return 1;
else return (1 / doubleFactorial(n) + Euler_Constant(n - 1));
}
}
}
欧拉常数(Euler-Mascheroni constant)
欧拉-马歇罗尼常数(Euler-Mascheroni constant)是一个主要应用于数论的数学常数。它的定义是调和级数与自然对数的差值。
学过高等数学的人都知道,调和级数S=1+1/2+1/3+……是发散的,证明如下:
由于ln(1+1/n)<1/n (n=1,2,3,…)
于是调和级数的前n项部分和满足
Sn=1+1/2+1/3+…+1/n>ln(1+1)+ln(1+1/2)+ln(1+1/3)+…+ln(1+1/n)
=ln2+ln(3/2)+ln(4/3)+…+ln[(n+1)/n]
=ln[2*3/2*4/3*…*(n+1)/n]=ln(n+1)
由于
lim Sn(n→∞)≥lim ln(n+1)(n→∞)=+∞
所以Sn的极限不存在,调和级数发散。
但极限S=lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)却存在,因为
Sn=1+1/2+1/3+…+1/n-ln(n)>ln(1+1)+ln(1+1/2)+ln(1+1/3)+…+ln(1+1/n)-ln(n)
=ln(n+1)-ln(n)=ln(1+1/n)
由于
lim Sn(n→∞)≥lim ln(1+1/n)(n→∞)=0
因此Sn有下界
而
Sn-S(n+1)=1+1/2+1/3+…+1/n-ln(n)-[1+1/2+1/3+…+1/(n+1)-ln(n+1)]
=ln(n+1)-ln(n)-1/(n+1)=ln(1+1/n)-1/(n+1)
将ln(1+1/n)展开,取其前两项,由于舍弃的项之和大于0,故
ln(1+1/n)-1/(n+1)>1/n-1/(2n^2)-1/(n+1)=1/(n^2+n)-1/(2n^2)>0
即ln(1+1/n)-1/(n+1)>0,所以Sn单调递减。由单调有界数列极限定理,可知Sn必有极限,因此
S=lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)存在。
于是设这个数为γ,这个数就叫作欧拉常数,他的近似值约为0.57721566490153286060651209,目前还不知道它是有理数还是无理数。在微积分学中,欧拉常数γ有许多应用,如求某些数列的极限,某些收敛数项级数的和等。例如求lim[1/(n+1)+1/(n+2)+…+1/(n+n)](n→∞),可以这样做:
lim[1/(n+1)+1/(n+2)+…+1/(n+n)](n→∞)=lim[1+1/2+1/3+…+1/(n+n)-ln(n+n)](n→∞)-lim[1+1/2+1/3+…+1/n-ln(n)](n→∞)+lim[ln(n+n)-ln(n)](n→∞)=γ-γ+ln2=ln2
4 代码格式
using System;namespace Legalsoft.Truffer.Algorithm
{public static partial class Number_Sequence{private static double doubleFactorial(int n){if (n == 1) return 1;else return n * doubleFactorial(n - 1);}public static double Euler_Constant(int n){if (n == 0) return 1;else return (1 / doubleFactorial(n) + Euler_Constant(n - 1));}}
}相关文章:

C#,欧拉常数(Euler Constant)的算法与源代码
1 欧拉常数 欧拉常数最先由瑞士数学家莱昂哈德 欧拉 (Leonhard Euler) 在1735年发表的文章《De Progressionibus harmonicus observationes》中定义。欧拉曾经使用γ作为它的符号,并计算出了它的前6位,1761年他又将该值计算到了16位 。 欧拉常数最先由瑞…...

asio监听eventfd
c - Does BOOST asio supports eventfd? like epoll - Stack Overflow asio的官方example并没有asio监听eventfd的例子,但asio支持posix::stream_descriptor, 如果将eventfd包装成posix::stream_descriptor,并注册到io_context里…...

《统计学简易速速上手小册》第9章:统计学在现代科技中的应用(2024 最新版)
文章目录 9.1 统计学与大数据9.1.1 基础知识9.1.2 主要案例:社交媒体情感分析9.1.3 拓展案例 1:电商销售预测9.1.4 拓展案例 2:实时交通流量分析 9.2 统计学在机器学习和人工智能中的应用9.2.1 基础知识9.2.2 主要案例:预测客户流…...
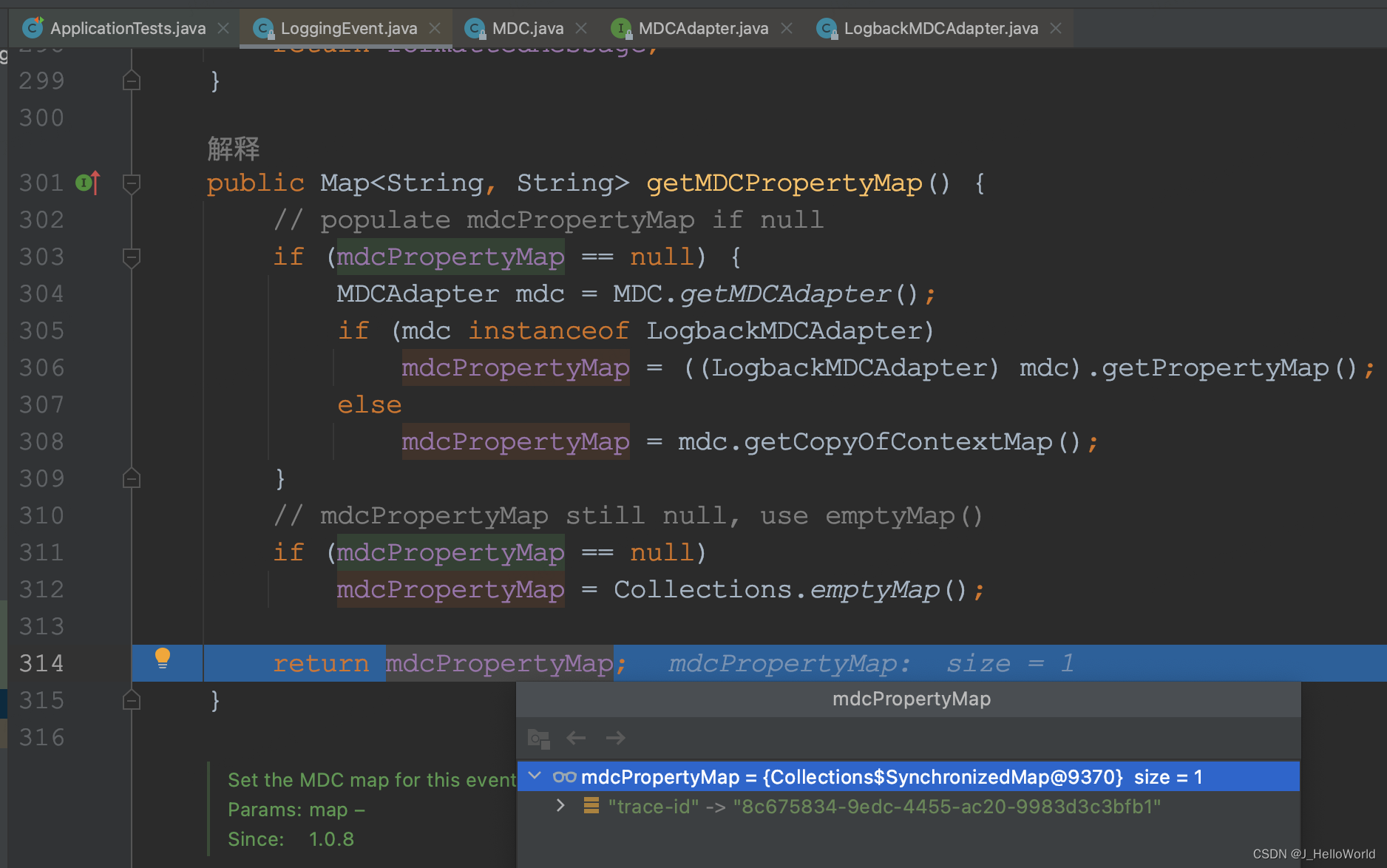
问题排查利器 - 分布式 trace
在分布式系统开发中,系统间的调用往往会横跨多个应用之间的接口。负责的调用链路也导致了,当线上环境出现问题时,例如请求失败、延迟增加或错误发生,我们无法第一时间确定是哪个环节出了问题,这给故障排查和修复带来了…...
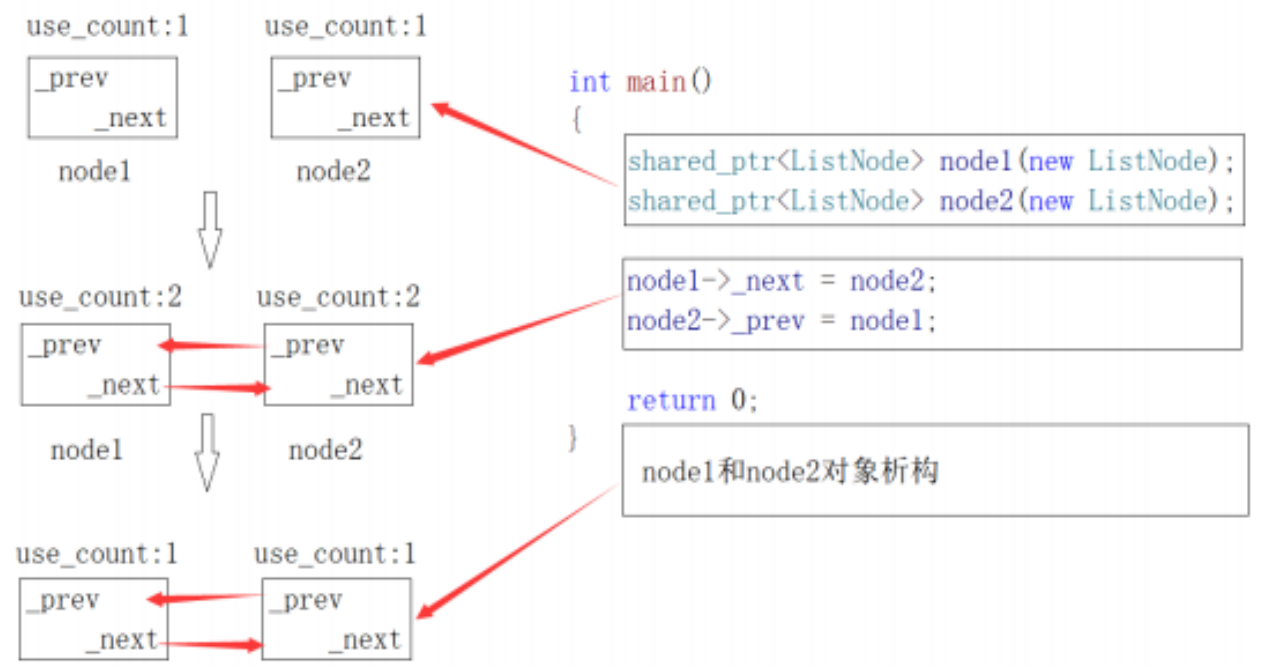
C++进阶(十四)智能指针
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、为什么需要智能指针?二、内存泄漏1、 什么是内存泄漏,内存泄漏的危…...

GPT最新进展:推出视频功能!迭代即将来临!
随着人工智能的不断进步,ChatGPT正准备以其全新的视频功能大跃进,同时,备受期待的GPT-5也即将在今年露面,预示着AI领域即将迎来一场变革。 在最近一期充满激情的Unconfuse Me播客中,OpenAI的首席执行官Sam Altman与技…...
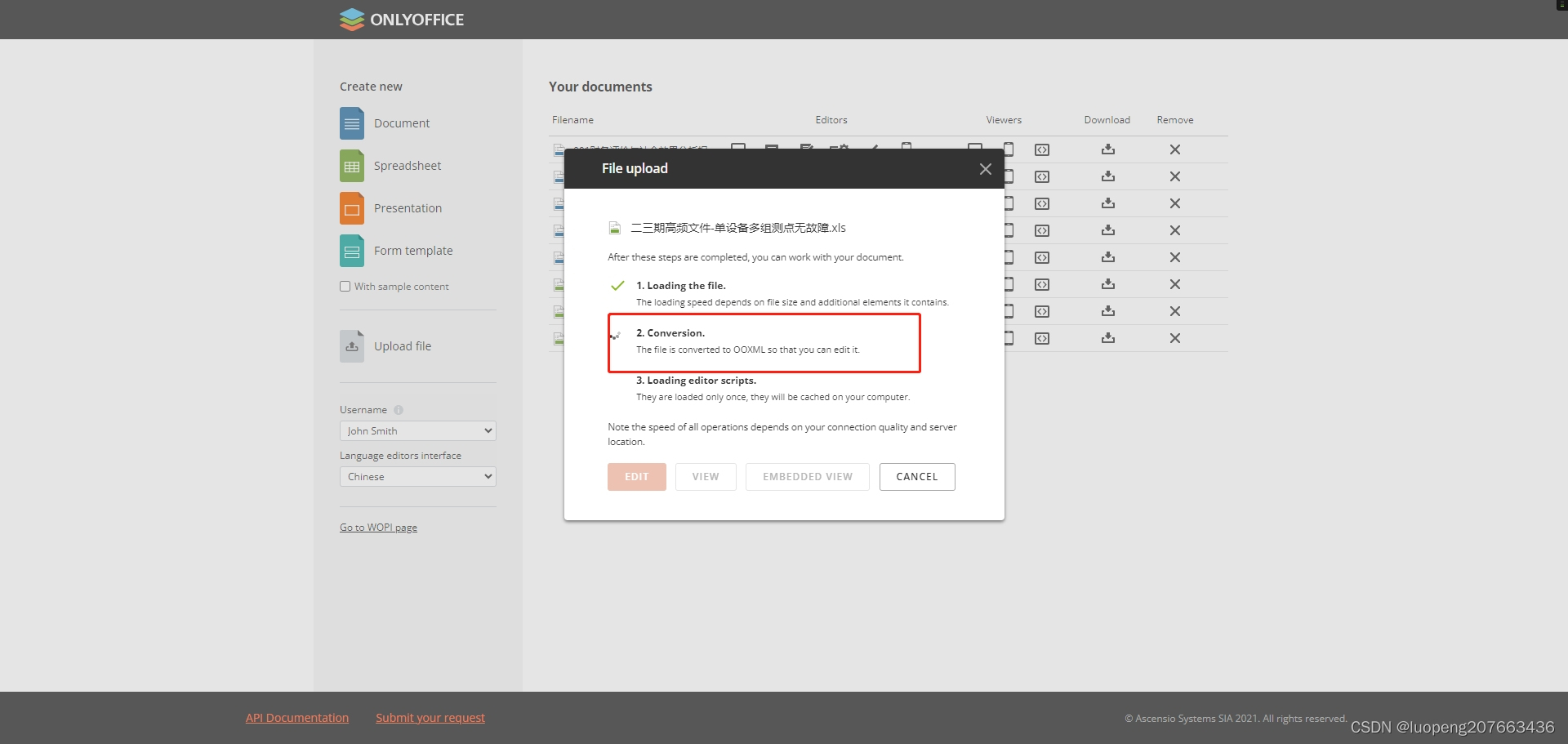
各款Excel、word在线预览工具对比分析以及onlyoffice预览Excel加载时间长的解决方案
对于onlyoffice插件预览慢的问题分析: 研究了一下onlyoffice,得出以下结论! 对于预览慢的问题,原因出在文件类型上,文件类型为低版本xls而非新版xlsx文件,onlyoffice服务器会自动将该文件转换为xlsx文件再…...

【课程作业_01】国科大2023模式识别与机器学习实践作业
国科大2023模式识别与机器学习实践作业 作业内容 从四类方法中选三类方法,从选定的每类方法中 ,各选一种具体的方法,从给定的数据集中选一 个数据集(MNIST,CIFAR-10,电信用户流失数据集 )对这…...

LeetCode374. Guess Number Higher or Lower——二分查找
文章目录 一、题目二、题解 一、题目 We are playing the Guess Game. The game is as follows: I pick a number from 1 to n. You have to guess which number I picked. Every time you guess wrong, I will tell you whether the number I picked is higher or lower th…...
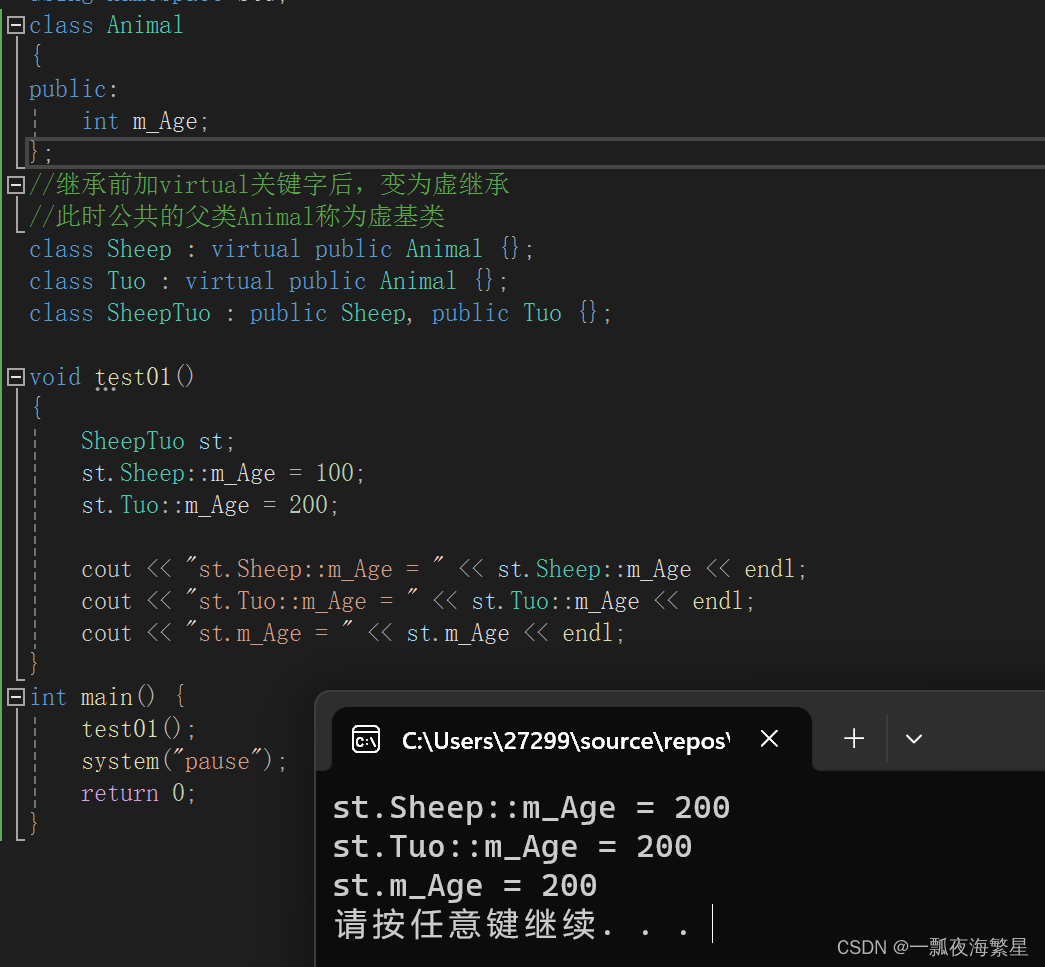
继承
1.继承的作用 有些类与类之间存在特殊关系,下级别的成员除了拥有上一级别的共性,还有自己的特性。 这个时候我们就可以考虑利用继承技术,减少重复代码。 总结: 继承的好处:可以减少重复的代码 class A : public B;…...

北斗卫星在物联网时代的应用探索
北斗卫星在物联网时代的应用探索 在当今数字化时代,物联网的应用已经深入到人们的生活中的方方面面,让我们的生活更加智能便捷。而北斗卫星系统作为我国自主研发的卫星导航系统,正为物联网的发展提供了强有力的支撑和保障。本文将全面介绍北…...

SQL注入 - 利用报错函数 floor 带回回显
环境准备:构建完善的安全渗透测试环境:推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 一、原理 利用COUNT(), FLOOR(), RAND(), 和 GROUP BY来生成主键重复错误 函数解释 count(): 这个函数用于计算满足某一条件下的行数,是SQL中的一个聚合函数,常用于统计查询结…...
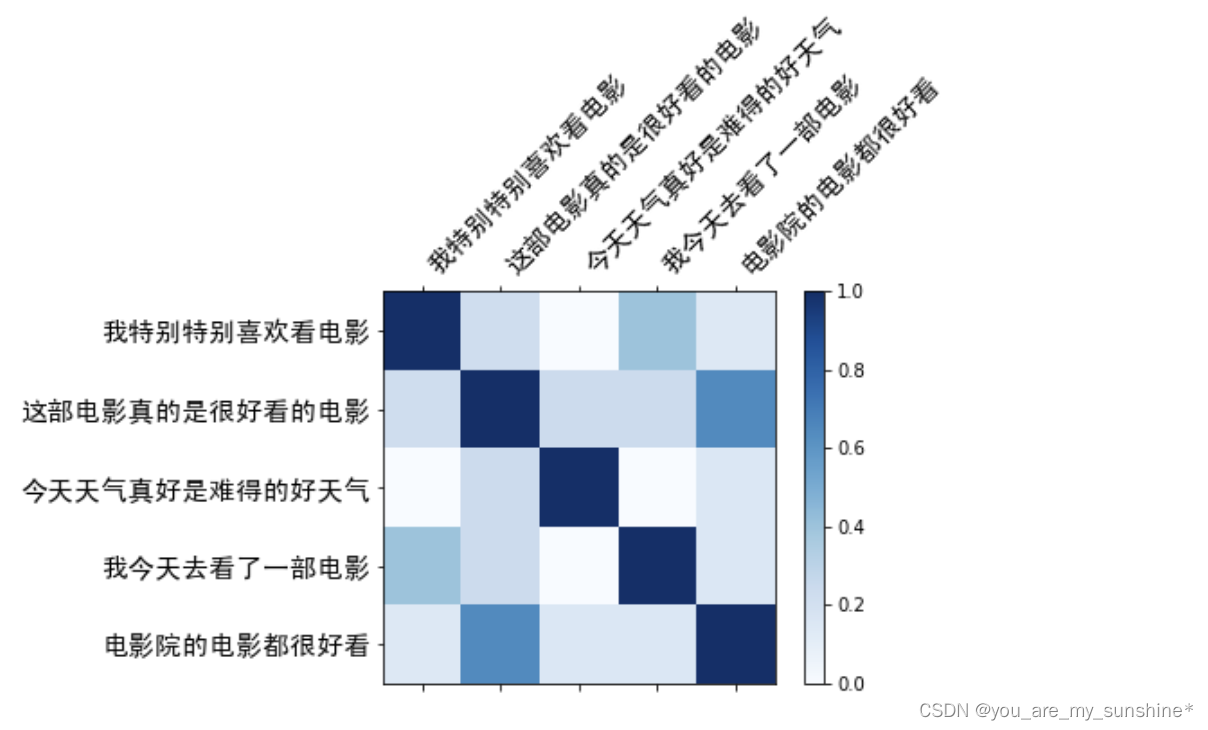
NLP_Bag-Of-Words(词袋模型)
文章目录 词袋模型用词袋模型计算文本相似度1.构建实验语料库2.给句子分词3.创建词汇表4.生成词袋表示5.计算余弦相似度6.可视化余弦相似度 词袋模型小结 词袋模型 词袋模型是一种简单的文本表示方法,也是自然语言处理的一个经典模型。它将文本中的词看作一个个独立…...
C语言rand随机数知识解析和猜数字小游戏
rand随机数 rand C语言中提供了一个可以随机生成一个随机数的函数:rand() 函数原型: int rand(void);rand函数返回的值的区间是:0~RAND_MAX(32767)之间。大部分编译器都是32767。 #include<stdlib.h> int ma…...

django中的缓存功能
一:介绍 Django中的缓存功能是一个重要的性能优化手段,它可以将某些耗时的操作(如数据库查询、复杂的计算等)的结果存储起来,以便在后续的请求中直接使用这些缓存的结果,而不是重新执行耗时的操作。Django…...
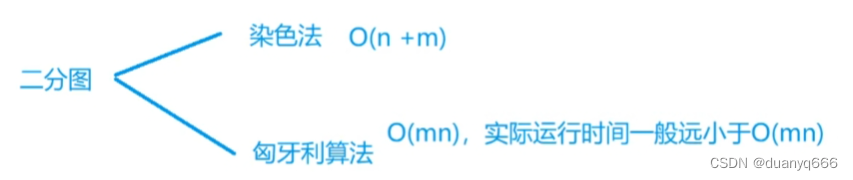
三、搜索与图论
DFS 排列数字 #include<iostream> using namespace std; const int N 10; int a[N], b[N]; int n;void dfs(int u){if(u > n){for(int i 1; i < n; i)cout<<a[i]<<" ";cout<<endl;return;}for(int i 1; i < n; i){if(!b[i]){b[…...
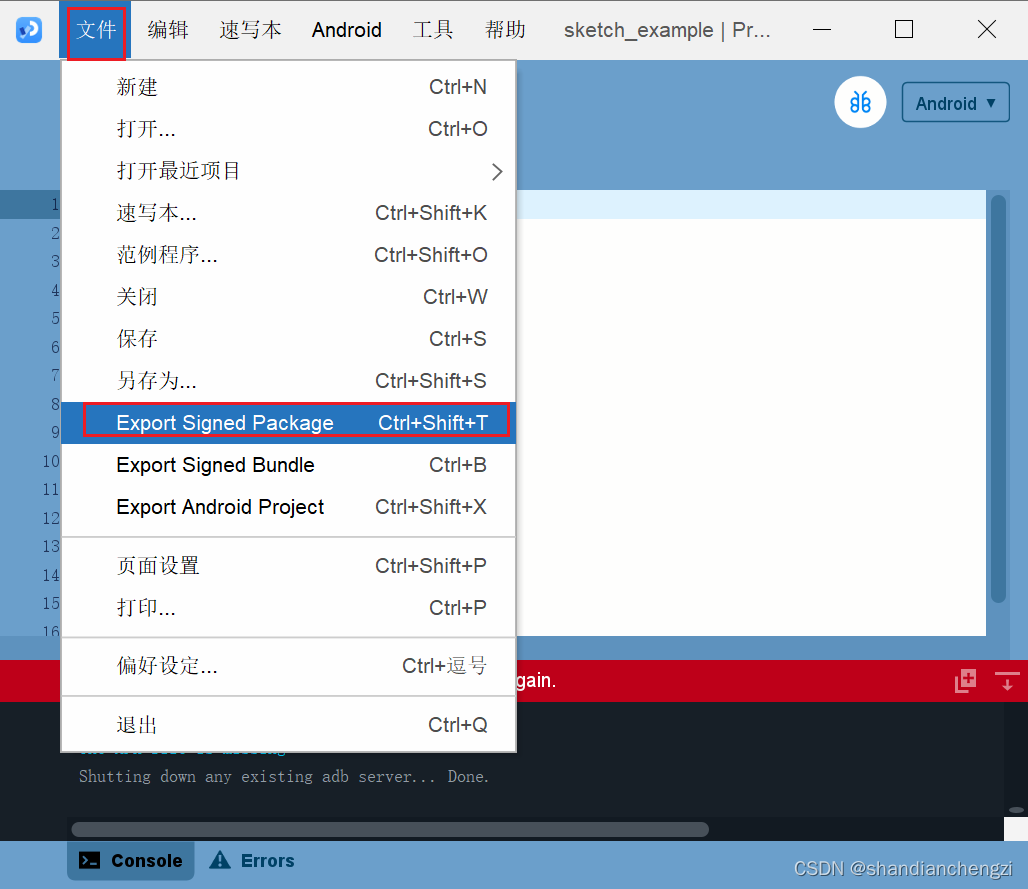
【翻译】Processing安卓模式的安装使用及打包发布(内含中文版截图)
原文链接在下面的每一章的最前面。 原文有三篇,译者不知道贴哪篇了,这篇干脆标了原创。。 译者声明:本文原文来自于GNU协议支持下的项目,具备开源二改授权,可翻译后公开。 文章目录 Install(安装࿰…...
MATLAB图像处理——边缘检测及图像分割算法
1.检测图像中的线段 clear clc Iimread(1.jpg);%读入图像 Irgb2gray(I); %转换为灰度图像 h1[-1, -1. -1; 2, 2, 2; -1, -1, -1]; %模板 h2[-1, -1, 2; -1, 2, -1; 2, -1, -1]; h3[-1, 2, -1; -1, 2, -1; -1, 2, -1]; h4[2, -1, -1; -1, 2, -1; -1, -1, 2]; J1imfilter(I, h1)…...

探索设计模式:原型模式深入解析
探索设计模式:原型模式深入解析 设计模式是软件开发中用于解决常见问题的标准解决方案。它们不仅能提高代码的可维护性和可复用性,还能让其他开发者更容易理解你的设计决策。今天,我们将聚焦于创建型模式之一的原型模式(Prototyp…...

IAR报错解决:Fatal Error[Pe1696]: cannot open source file “zcl_ha.h“
报错信息 Fatal Error[Pe1696]: cannot open source file "zcl_ha.h" K:\Z-Stack 3.0.2\Projects\zstack\Practice\SampleSwitch\Source\zcl_samplesw_data.c 51 意思是找不到zcl_ha.h文件 找不到的理由可能是我把例程复制了一份到别的文件目录下,少复制…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
