Peter算法小课堂—背包问题
我们已经学过好久好久的动态规划了,动态规划_Peter Pan was right的博客-CSDN博客
那么,我用一张图片来概括一下背包问题。

大家有可能比较疑惑,优化决策怎么优化呢?答案是,滚动数组,一个神秘而简单的东西。
01背包
题目:小偷来你家,他带的包只能装c斤的财务。你家有n种财务,分别重w1、w2......wn斤,价值分别为v1、v2......,请输出能拿走的最大总价值?
大家思考一下状态定义和状态转移方程。
额……
状态定义
f[i][j]:用前i个物品,每个物品只能选或不选,满足重量和小于等于j的所有选法中,价值最高的那个方案。最终答案:f[n][c]
状态转移方程
首先,我们分两种情况讨论:1.选i 2.不选i
1。 此时我们重量和会变小w[i],但是价值会增加v[i],f[i][j]=f[i-1][j-w[i]]+v[i]
2。 此时物品数减1,f[i][j]=f[i-1][j]
最后,再取最大值,得到状态转移方程:f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i])
代码①
for(int i=1;i<=n;i++) cin>>w[i]>>v[i];
for(int i=1;i<=n;++i){for(int j=1;j<=c;++j){if(w[i]>j) f[i][j]=f[i-1][j];else f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);}
}
cout<<f[n][c]<<endl;有点费空间,要开滚动数组
代码②
滚动数组,给大家看个图

我们发现,dp[i][j]这一格,只需要i-1这一行,i-2、i-3……都不需要。题目如果并没有要求中间的状态(比如输出背包的方案),我们就可以将其省略来节省空间的使用。所以我们可以只用一维数组dp[j]来记录数据dp[i][j]的状态,在更新的过程中不断用新的数据dp[j] (dp[i][j]) 覆盖掉旧的数据dp[j](dp[i-1][j])。大家听懂了吗???
代码呢?
#include <bits/stdc++.h>
using namespace std;
const int MAXC=2009;
int n,c,w,v,f[MAXC];
int main(){cin>>c>>n;for(int i=1;i<=n;i++){cin>>w>>v;for(int j=c;j>=w;j--)f[j]=max(f[j],f[j-w]+v);}cout<<f[c]<<endl;return 0;
}大家可能会疑惑,为什么第二层循环要倒着推啊,我给出一个解释。我们每次计算dp[j] (即dp[i][j]) 的时候都会需要dp[j-w[i]] (即dp[i-1][j-w[i]])的值。所以如果我们正序计算,那么dp[j-w[i]]就已经更新了 (即用过之前的背包了),与每个背包只能用1次不符。那么,这不就是完全背包要的吗?
完全背包
题目:小偷来你家,他带的包只能装c斤的财务。你家有n种财务,每种数量无限多,分别重w1、w2......wn斤,价值分别为v1、v2......,请输出能拿走的最大总价值?
题解请看01背包,这里只给出代码
cin>>c>>n;
for(int i=1;i<=n;i++){cin>>w>>v;for(int j=w;j<=c;j++)f[j]=max(f[j],f[j-w]+v);
}
cout<<f[c]<<endl;分组背包


分组01与普通01的区别就是,分组01有两组策略:1.选择本组的某一件 2.一件不选

所以说,分组背包编码很麻烦
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll G=19;
const ll N=39;
const ll MAXV=209;
ll c,n,g,f[MAXV];
vector<ll> w[G],v[G];
int main(){cin>>c>>n>>g;for(ll i=1;i<=n;i++){ll ww,vv,p;cin>>ww>>vv>>p;w[p].push_back(ww);v[p].push_back(vv);}for(ll i=0;i<=g;i++){//枚举组号for(ll j=c;j>=0;j--){//枚举载重for(ll k=0;k<w[i].size();k++){//枚举物品if(j>=w[i][k]) f[j]=max(f[j],f[j-w[i][k]]+v[i][k]);}}}cout<<f[c]<<endl;return 0;
}多重背包

多重背包怎么办呢,这里,我们要采用二进制拆分。

就是……这样
void bb01(int w,int v){for(int j=c;j>=w;j--)f[j]=max(f[j],f[j-w]+v);
}
int main(){cin>>n>>c;for(int i=1;i<=n;i++){cin>>w>>v>>s;for(int k=1;k<=s;s-=k;k*=2) bb01(k*w,k*v);if(s) bb01(s*w,s*v);}cout<<f[c]<<endl;return 0;
}简单吧,其实为什么这里我都没有进行仔细的讲解,是因为……不会,再多思考思考01背包和图片。
混合背包
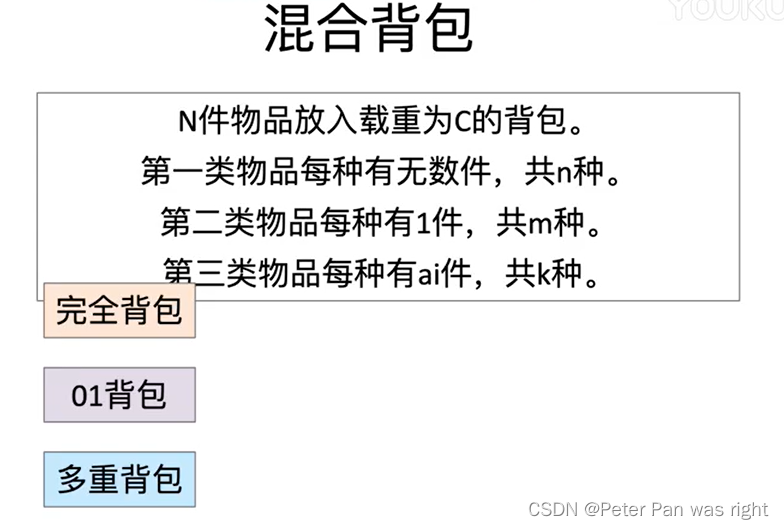
大家试着写写。大家有兴趣的话可以去往上搜搜“背包九讲”。
希望这些对大家有用,三连必回
相关文章:

Peter算法小课堂—背包问题
我们已经学过好久好久的动态规划了,动态规划_Peter Pan was right的博客-CSDN博客 那么,我用一张图片来概括一下背包问题。 大家有可能比较疑惑,优化决策怎么优化呢?答案是,滚动数组,一个神秘而简单的东西…...

网易腾讯面试题精选----50 个 Git 面试问题
介绍 Git 是 DevOps 之旅的起点。所以,我只是概述了 50 个快速问题以及 Git 的答案。这些问题非常快,你可以在 DevOps 面试中问。它适合初学者到中级水平。 面试问答 1.问:什么是Git? 答:Git 是一个分布式版本控制系统,允许多个开发人员在一个项目上进行协作并跟踪源代…...

Android CMakeLists.txt语法详解
一.CMake简介 你或许听过好几种 Make 工具,例如 GNU Make ,QT 的 qmake ,微软的 MSnmake,BSD Make(pmake),Makepp,等等。这些 Make 工具遵循着不同的规范和标准,所执行的…...

Vue3快速上手(二)VSCode官方推荐插件安装及配置
一、VSCode官方插件安装,如下图2款插件 在用vite创建的程序里,提示提安装推荐的插件了,如下图: 二、配置 在设置-扩展里找到Volar插件,将Dot Value勾选上。这样在ref()修改变量时,会自动填充.value,无需…...

等保2、3级所需设备
三级等保要求及所需设备 《等级保护基本要求》所需设备 结构安全(G3) b)应保证网络各个部分的宽带满足业务高峰期需要; g)应按照对业务服务的需要次序来指定宽带分配优先级别,保证在网络发生拥堵的时候优先保护重要主机 负载均衡…...
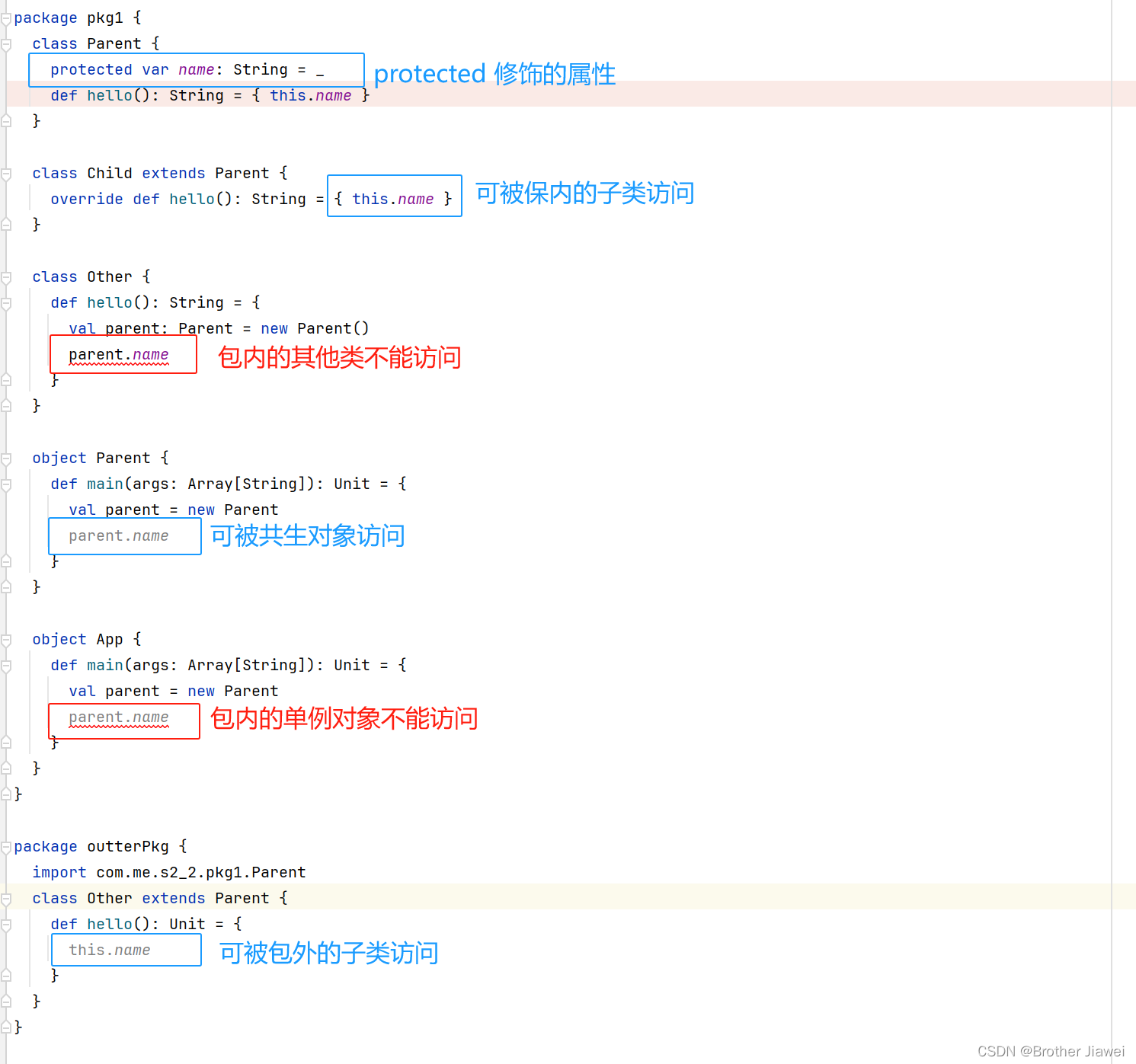
6 scala-面向对象编程基础
Scala 跟 Java 一样,是一门面向对象编程的语言,有类和对象的概念。 1 类与对象 与 Java 一样,Scala 也是通过关键字 class 来定义类,使用关键字 new 创建对象。 要运行我们编写的代码,同样像 Java 一样,…...
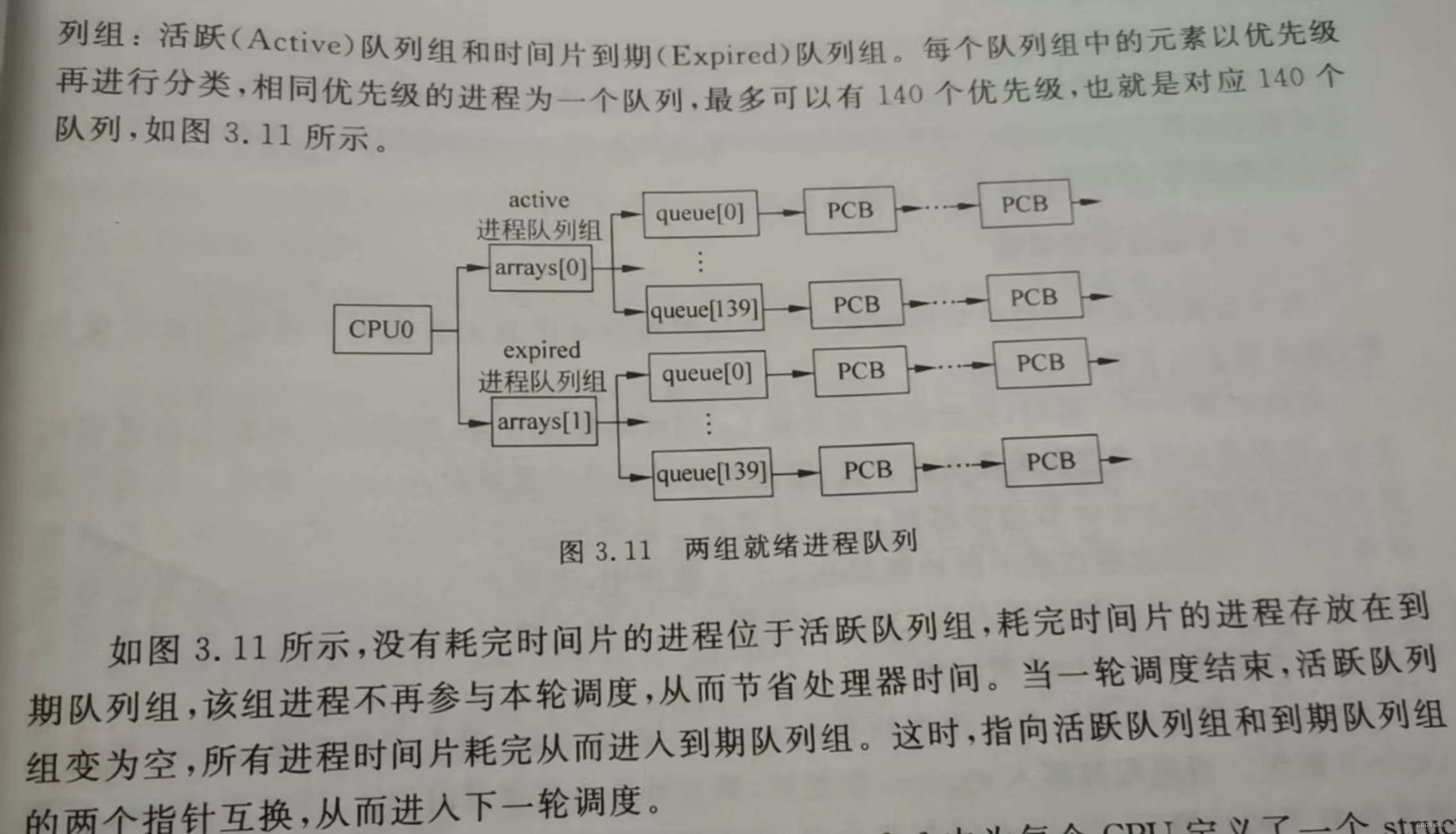
【linux温故】linux调度机制
假如你是设计者,你会设计怎样的调度机制呢? 时间片 最简单的,小学生都能想出来的一种,每个 ready task,按照一个固定的时间片轮流执行。 大家不要抢,挨个儿排队执行。执行完时间片,就排在后面…...

django中如何使用mysql连接池
一:介绍 在Django中使用MySQL时,通常情况下,Django的数据库层会为你管理数据库连接。Django的数据库接口是线程安全的,这意味着它会自动为每个线程创建和管理数据库连接。在大多数情况下,你不需要手动创建线程池来管理…...

3D高斯溅射:面向三维场景的实时渲染技术
1. 前言 高斯溅射技术【1】一经推出,立刻引起学术界和工业界的广泛关注。相比传统的隐式神经散射场渲染技术,高斯溅射依托椭球空间,显性地表示多目图像的三维空间关系,其计算效率和综合性能均有较大的提升,且更容易理…...
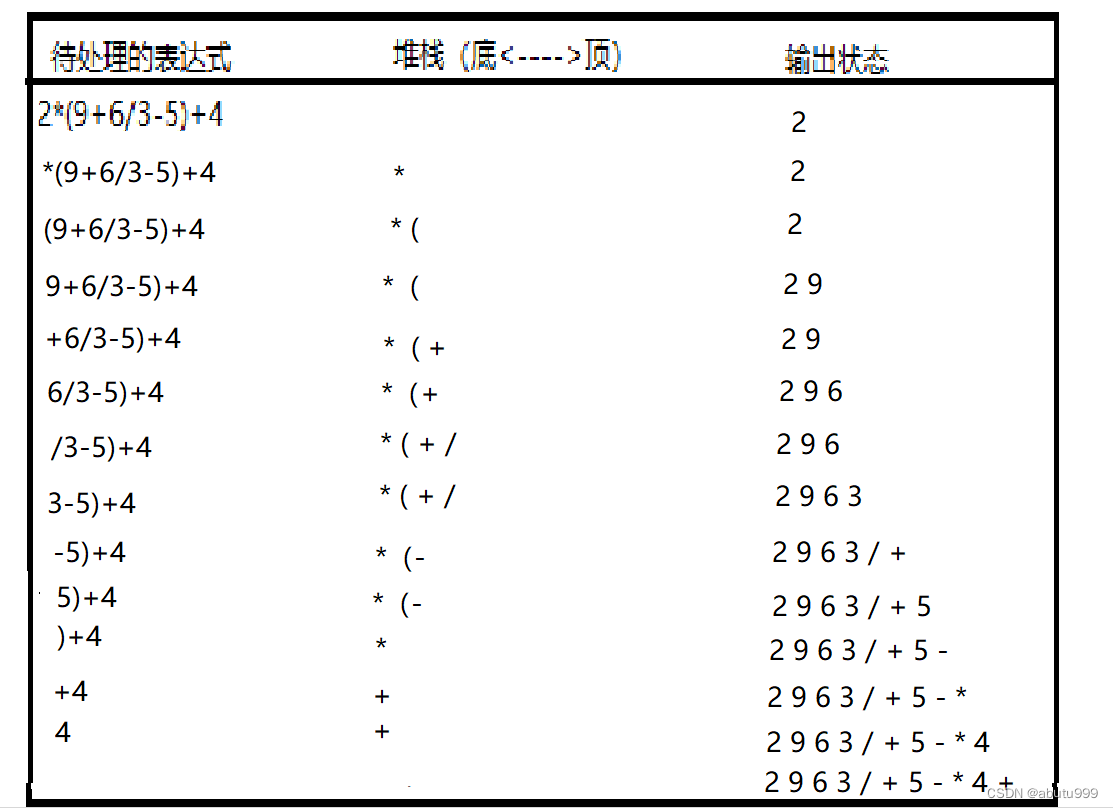
【数据结构】13:表达式转换(中缀表达式转成后缀表达式)
思想: 从头到尾依次读取中缀表达式里的每个对象,对不同对象按照不同的情况处理。 如果遇到空格,跳过如果遇到运算数字,直接输出如果遇到左括号,压栈如果遇到右括号,表示括号里的中缀表达式已经扫描完毕&a…...
-视图的创建和应用)
MySQL进阶查询篇(9)-视图的创建和应用
数据库视图是MySQL中一个非常重要的概念。它是一个虚拟表,由一个查询的结果集组成。数据库视图为用户提供了一种简化数据查询和操作的方式。本文将介绍MySQL数据库视图的创建和应用。 1. 创建数据库视图 要创建MySQL数据库视图,我们使用CREATE VIEW语句…...
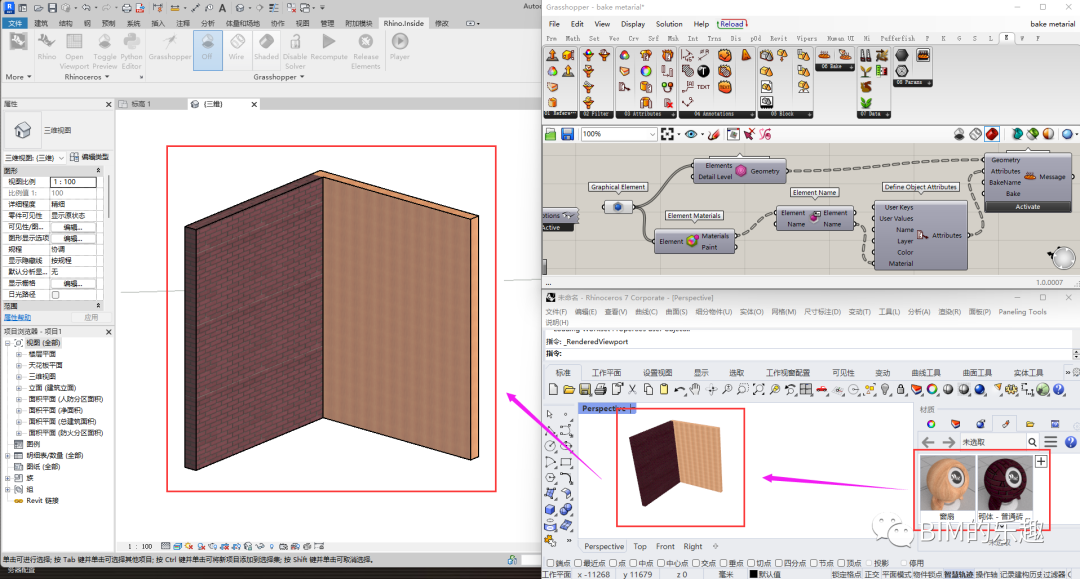
Rhino.Inside带材质将Revit模型bake到Rhino
Hello大家好!我是九哥~ 今天来讲一个小技巧,就是我通常采用RIR将Revit的模型的Geometry Bake到Rhino,肯定是没有材质的,那么如果我们需要带材质那要怎么办呢? 对于会的人,其实挺简单的,只需要…...

随记-Java项目处理SQL注入问题
现象:http://10.xx.xx.xx:xx/services/xxService 存在SQL注入情况 加固意见: 需要对网站所有参数中提交的数据进行过滤,禁止输入“"、"xor"、"or"、”--“、”#“、”select“、”and“等特殊字符;所有…...

精读《js 模块化发展》
1 引言 如今,Javascript 模块化规范非常方便、自然,但这个新规范仅执行了 2 年,就在 4 年前,js 的模块化还停留在运行时支持,10 年前,通过后端模版定义、注释定义模块依赖。对经历过来的人来说,…...
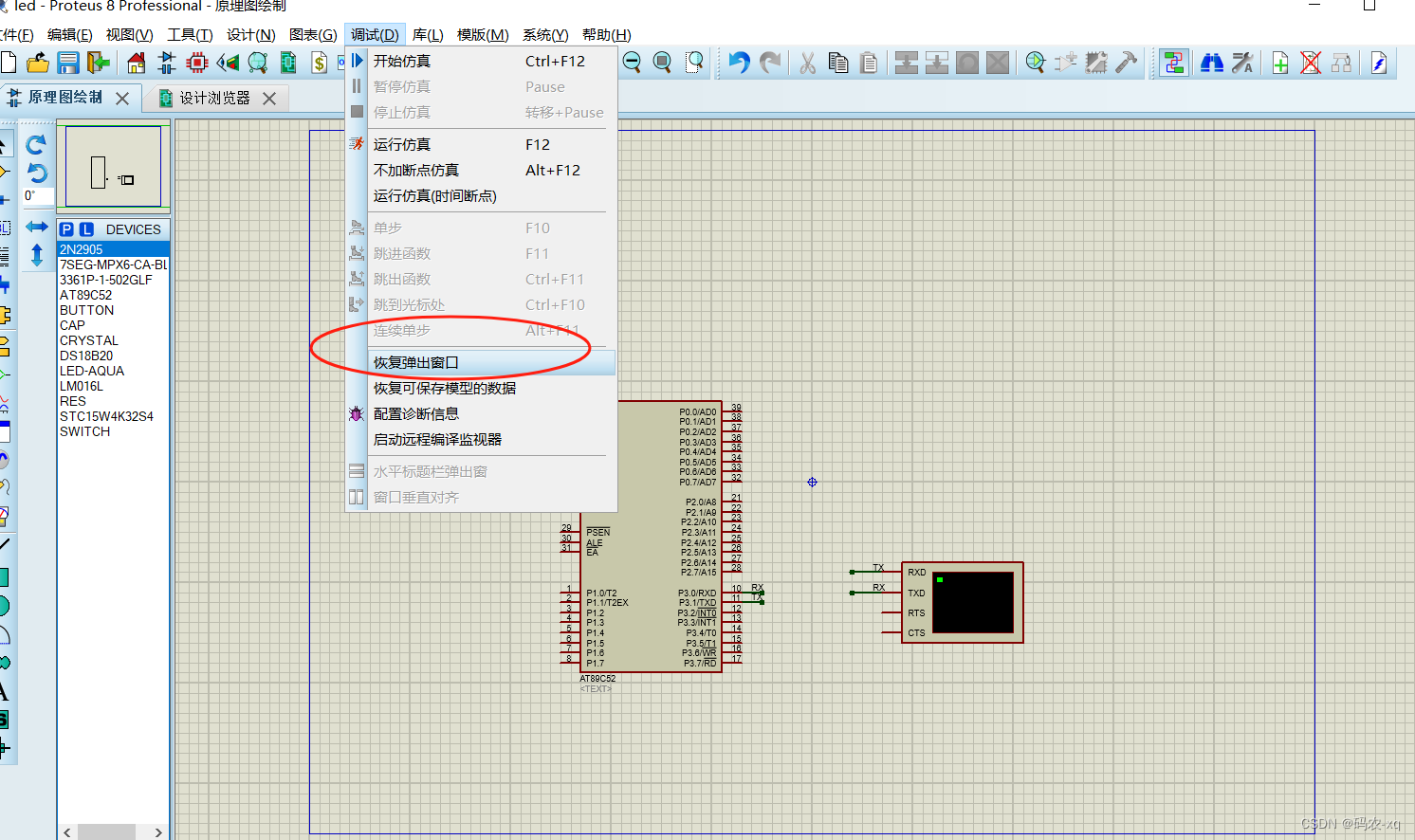
Proteus -模拟串口被关闭后怎样打开
Proteus -模拟串口被关闭后怎样打开 点击恢复弹出窗口,即可重新打开...

【深度学习】pytorch 与 PyG 安装(pip安装)
【深度学习】pytorch 与 PyG 安装(pip安装) 一、PyTorch安装和配置(一)、安装 CUDA(二)、安装torch、torchvision、torchaudio三个组件(1)下载镜像文件(2)创建…...

Bert与ChatGPT
1. Bert模型 BERT(Bidirectional Encoder Representations from Transformers)是一种预训练语言表示的方法,由Google AI在2018年提出。它标志着自然语言处理(NLP)领域的一个重大进步,因为它能够理解单词在…...
微信自动预约小程序开发指南:从小白到专家
随着互联网的发展,小程序已经成为了一个备受欢迎的在线预约平台。本文将详细介绍如何使用第三方制作平台,如乔拓云网,来搭建一个从入门到精通的预约小程序。 首先,我们需要登录乔拓云网,并选择一个适合自己的小程序模板…...
)
巴尔加瓦算法图解【完结】:算法运用(下)
目录 布隆过滤器HyperLogLogSHA算法比较文件检查密码 Diffie-Hellman密钥交换线性规划结语(完结) 布隆过滤器 在元素很多的情况下,判断一个元素是否在集合中可以使用布隆过滤器。布隆过滤器(Bloom Filter)是 1970 年由…...
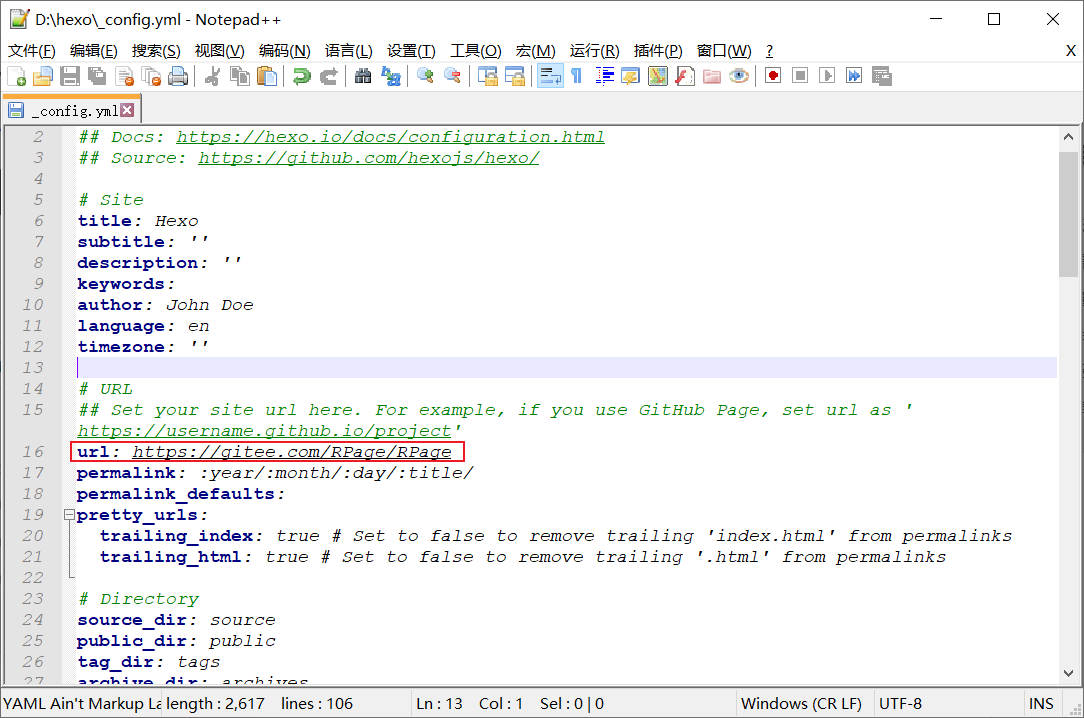
hexo部署到gitee(码云)
引言 Hexo 是一个基于Node.js的静态博客框架,而 Gitee(也被称为码云)是一个国内的代码托管平台,支持 Git 版本控制系统,与 GitHub 类似。将 Hexo 部署到 Gitee Pages 可以让你的博客受益于 Gitee 的国内服务器…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
