二叉树 ---- 所有结点数
普通二叉树的结点数:
递归法:
对二叉树进行前序or后序遍历:
typedef struct Tree
{int data;Tree* leftChild;Tree* rightChild;
}tree,*linklist;
//计算普通二叉树的结点数
int nodenums(linklist node)
{if(node == nullptr) return 0; //node为空就返回0int leftnums = nodenums(node->leftChild); //左子树的数量通过递归计算出来int rightnums = nodenums(node->rightChild); //右子树的数量通过递归计算出来return leftnums + rightnums + 1;返回左子树的数量 + 右子树的数量 + 1(根结点的数量)
}化简写法:
typedef struct Tree
{int data;Tree* leftChild;Tree* rightChild;
}tree,*linklist;
//计算普通二叉树的结点数
int nodenums(linklist node)
{if(node == nullptr) return 0;return 1 + nodenums(node->leftChild) + nodenums(node->rightChild);
}队列法:
利用BFS的思想层序遍历:
#include <queue>
typedef struct Tree
{int data;Tree* leftChild;Tree* rightChild;
}tree,*linklist;
//法二(BFS)
int coutnode(linklist node)
{queue<linklist> q; //建立新的linklist型队列qif(node == nullptr) q.push(node); //如果node不为空,就把结点node推进队列int result = 0;//result用来存结点数//BFS层序遍历while(q.empty()){int size = q.size();for(int i = 0;i < size;i++){linklist p = q.front();q.pop();result++; //记录结点数if(p->leftChild) q.push(node->leftChild);if(p->rightChild) q.push(node->rightChild);}}return result;
}完全二叉树的结点数:
完全二叉树的本身会包含满二叉树,可以简便写,先判断最大的满二叉树的位置然后再利用普通二叉树的递归遍历方法进行计算。
如果遇到满二叉树,则返回满二叉树的结点数,可以利用公式2^n-1,利用位运算(2 << n) - 1。
(n为深度),也可以利用我前面的文章讲述的快速幂利用递归求出二次幂。
int nodenum(linklist node)
{if(node == nullptr) return 0;linklist left = node->leftChild;linklist right = node->rightChild;//左右子树深度int leftdepth = 0;int rightdepth = 0;while(left){left = left->leftChild;leftdepth++;}while(right){right = right->rightChild;rightdepth++;}//如果左右子树的深度相等就是满二叉树if(leftdepth == rightdepth) return (2 << leftdepth) - 1;//满二叉树的计算结点公式2^n-1return 1 + nodenum(node->leftChild) + nodenum(node->rightChild);
}判断平衡二叉树:
二叉树中任意结点的左右子树的深度相差不超过 1,那么它就是一棵平衡二叉树 。
所以abs(左子树深度 - 右子树深度) > 1就不是平衡二叉树。
所以先按照最大深度的计算方法递归左右子树的最大深度然后判断是否符合平衡二叉树,如果不是就return返回false,最后return返回平衡二叉树的最大深度。
typedef struct Tree
{int data;Tree* leftChild;Tree* rightChild;
}tree,*linklist;
//如果不是平衡二叉树,那么就返回-1记录其不是平衡二叉树
int balancedepth(linklist node)
{int leftdepth = balancedepth(node->leftChild);if(leftdepth == -1) return -1;int rightdepth = balancedepth(node->rightChild);if(rightdepth == -1) return -1;if(abs(leftdepth - rightdepth) > 1) return -1;//不平衡return 1 + max(leftdepth , rightdepth);
}输入一棵二叉树的根结点,判断该树是不是平衡二叉树。
如果某二叉树中任意结点的左右子树的深度相差不超过 1,那么它就是一棵平衡二叉树。
注意:
- 规定空树也是一棵平衡二叉树。
数据范围
树中节点数量 [0,500]。
样例
输入:二叉树[5,7,11,null,null,12,9,null,null,null,null]如下所示,5/ \7 11/ \12 9输出:true
struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:bool isBalanced(TreeNode* root) {int res = dfs(root);if(res != -1) return true;else return false;}int dfs(TreeNode* root){if(!root) return 0;int leftdepth = dfs(root->left),rightdepth = dfs(root->right);if(leftdepth == -1 || rightdepth == -1) return -1;if(abs(rightdepth - leftdepth) > 1) return -1;return 1 + max(leftdepth , rightdepth);}
};今天内容到这里了,感谢收看。
相关文章:

二叉树 ---- 所有结点数
普通二叉树的结点数: 递归法: 对二叉树进行前序or后序遍历: typedef struct Tree {int data;Tree* leftChild;Tree* rightChild; }tree,*linklist; //计算普通二叉树的结点数 int nodenums(linklist node) {if(node nullptr) return 0; …...
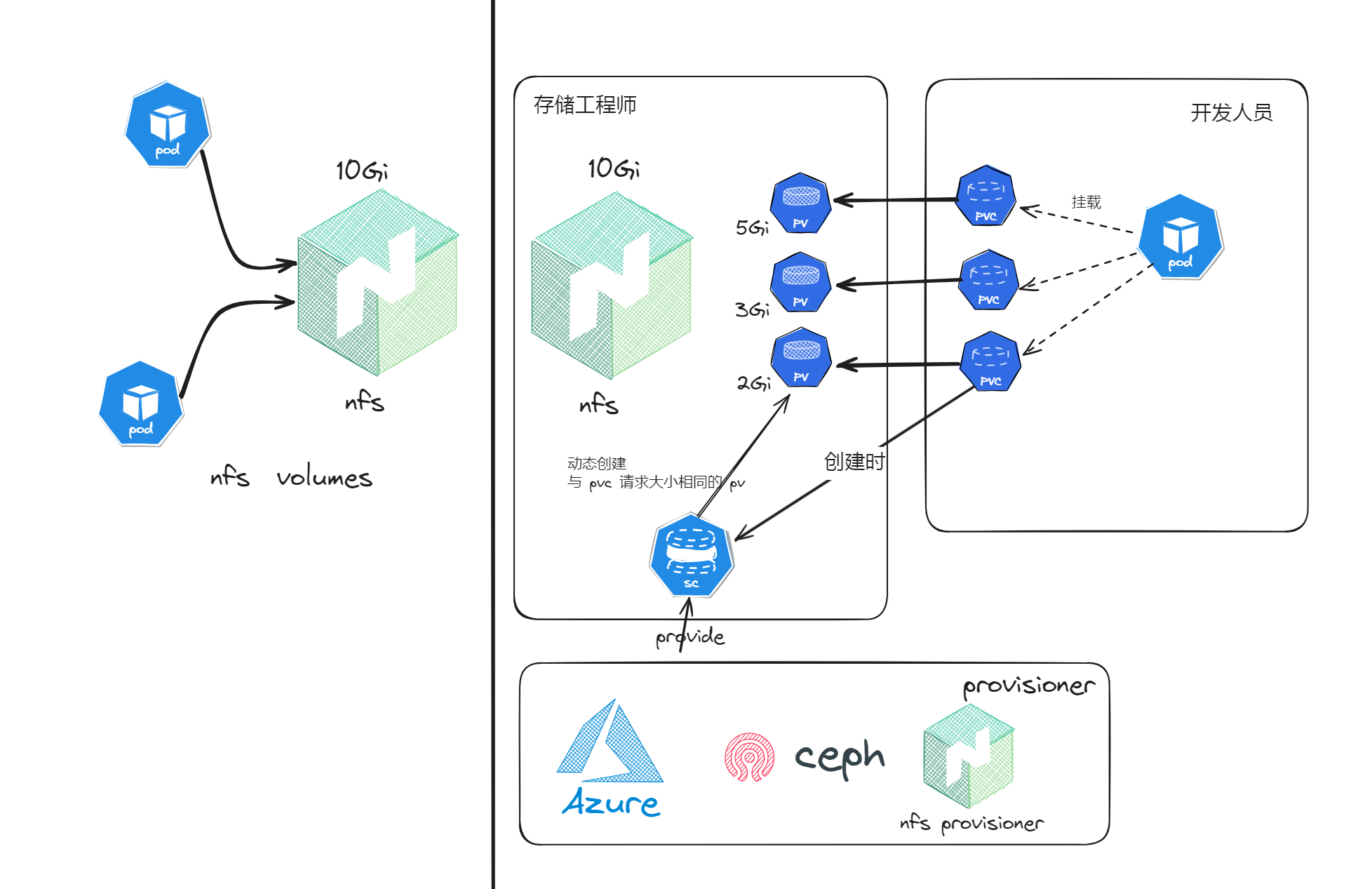
步步深入 k8s 使用 pv pvc sc 在 nfs 基础上共享存储
博客原文 文章目录 前言集群环境nfs 环境搭建pod 挂载 nfs架构图 pvc 方式挂载 nfs架构图 storageclass 方式动态申请 pv架构图 参考 前言 持久化卷(Persistent Volume, PV)允许用户将外部存储映射到集群,而持久化卷申请(Persist…...
Stable Diffusion 模型下载:Disney Pixar Cartoon Type A(迪士尼皮克斯动画片A类)
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十...
Modelsim10.4安装
简介(了解,可跳过) modelsim是Mentor公司开发的优秀的HDL语言仿真软件。 它能提供友好的仿真环境,采用单内核支持VHDL和Verilog混合仿真的仿真器。它采用直接优化的编译技术、Tcl/Tk技术和单一内核仿真技术,编译仿真速…...
Java基于微信小程序的医院核酸检测服务系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
VC++ 绘制折线学习
win32 有三个绘制折线的函数; Polyline,根据给定点数组绘制折线; PolylineTo,除了绘制也更新当前位置; PolyPolyline,绘制多条折线,第一个参数是点数组,第二个参数是一个数组、指…...

速盾:dns解析和cdn加速的区别与联系
DNS解析和CDN加速是两种不同的网络技术,但在网站访问过程中起到了相互协作的作用。 首先,DNS解析(Domain Name System)是将域名转换为IP地址的过程。当用户输入一个网址时,计算机会先向本地DNS服务器发送一个查询请求…...
C++ Qt框架开发 | 基于Qt框架开发实时成绩显示排序系统(3) 保存表格数据
对上两篇篇的工作C Qt框架开发| 基于Qt框架开发实时成绩显示排序系统(1)-CSDN博客和C Qt框架开发 | 基于Qt框架开发实时成绩显示排序系统(2)折线图显示-CSDN博客继续优化,增加一个保存按钮,用于保存成绩数据…...

ChatGPT 4:新特性与优势
ChatGPT 4:新特性与优势 一、引言 ChatGPT 4是一款备受瞩目的人工智能模型,它以其强大的语言生成能力和智能回答能力,为用户提供了更高效、更便捷的对话体验。为了能够充分享受ChatGPT 4的各项功能,本文将向您详细介绍其新特性&…...

【教程】MySQL数据库学习笔记(二)——数据类型(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【MySQL数据库学习】系列文章 第一章 《认识与环境搭建》 第二章 《数据类型》 文章目录 【MySQL数据库学习】系列文章一、整…...

Servo的并发模型介绍
Servo是一个由Mozilla Research开发的实验性浏览器引擎,旨在为未来的网页和应用程序提供高性能的渲染。Servo的并发模型是其核心特点之一,它利用现代多核处理器的优势,通过异步编程和并行处理来提高渲染效率和响应性。以下是对Servo并发模型的…...
Vue3大事件项目(ing)
文章目录 核心内容1.大事件项目介绍2.大事件项目创建3.Eslint配置代码风格4.配置代码检查工作流问题: pnpm lint是全量检查,耗时问题,历史问题 5.目录调整6.vue-router4 路由代码解析7.引入 Element Plus 组件库8.Pinia 构建仓库 和 持久化9.Pinia 仓库统一管理 核心内容 Vue3…...
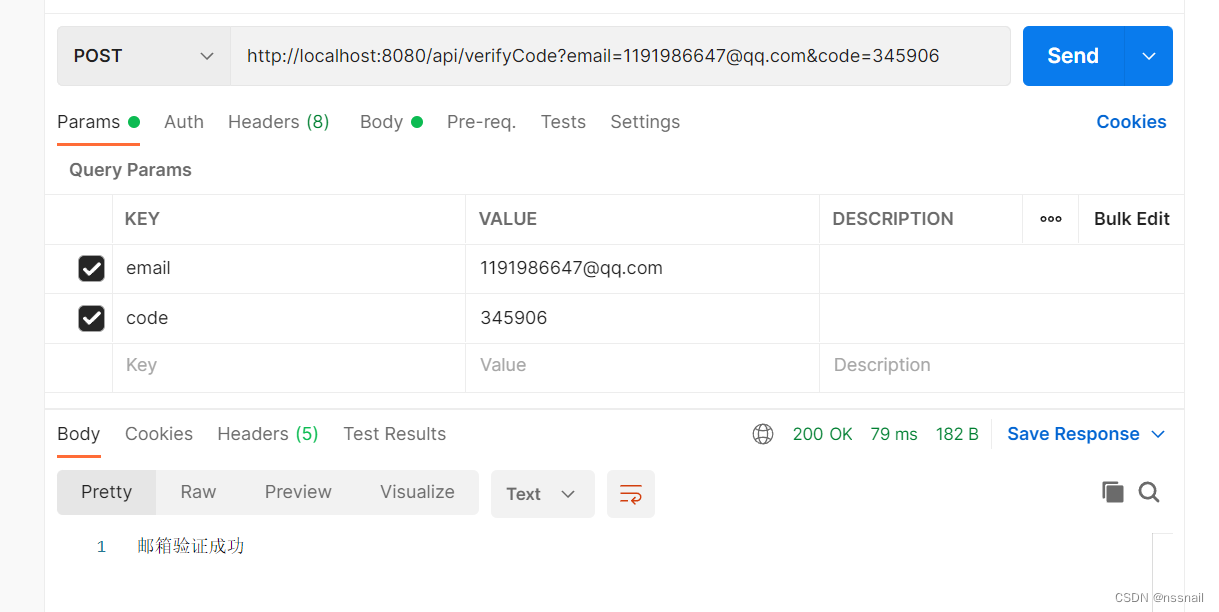
基于spring boot实现邮箱发送和邮箱验证
目录 一、邮箱发送实现1. 开通邮箱服务2. 添加邮箱依赖3.添加配置4.添加邮箱通用类5. 测试类 二、邮箱验证实现1.添加依赖2. 添加配置3.添加controller4. 测试 项目地址: https://gitee.com/nssnail/springboot-email 一、邮箱发送实现 1. 开通邮箱服务 使用qq邮箱、163邮箱都…...

华清作业day56
SQLite特性: 零配置一无需安装和管理配置;储存在单一磁盘文件中的一个完整的数据库;数据库文件可以在不同字节顺序的机器间自由共享;支持数据库大小至2TB;足够小,全部源码大致3万行c代码,250KB…...

【FPGA】VHDL:八段码到8421BCD码转换电路
目录 EDA设计基础练习题 : 实验要求如下: 代码 八段码到8421BCD码转换电路 8421BCD码到八段码转换电路 八段码到8421BCD~运行结果展示 8421BCD转八段码~运行结果展示 特别注意 软件:Quartus II 13.0 (64-bit) 语言:VHDL E…...
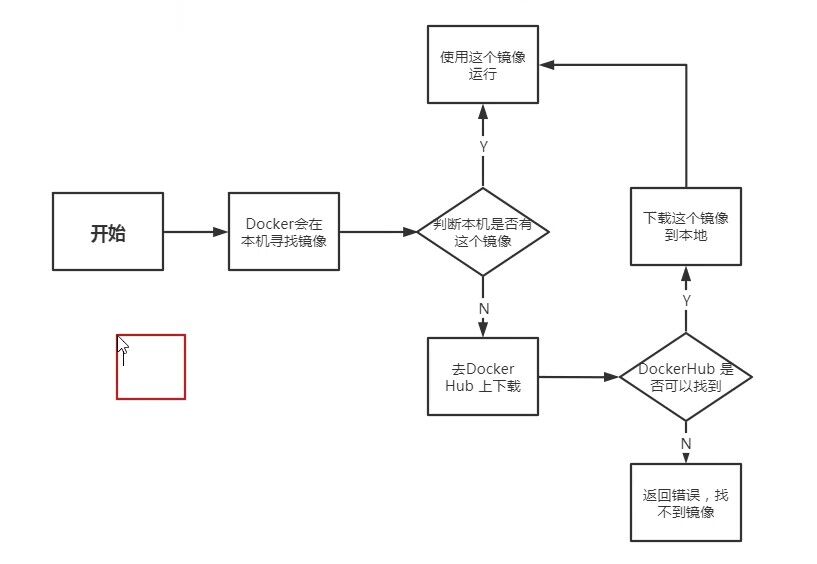
docker安装、运行
1、安装 之前有docker的话,需要先卸载旧版本: sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine 安装之前需要安装yum工具: sud…...
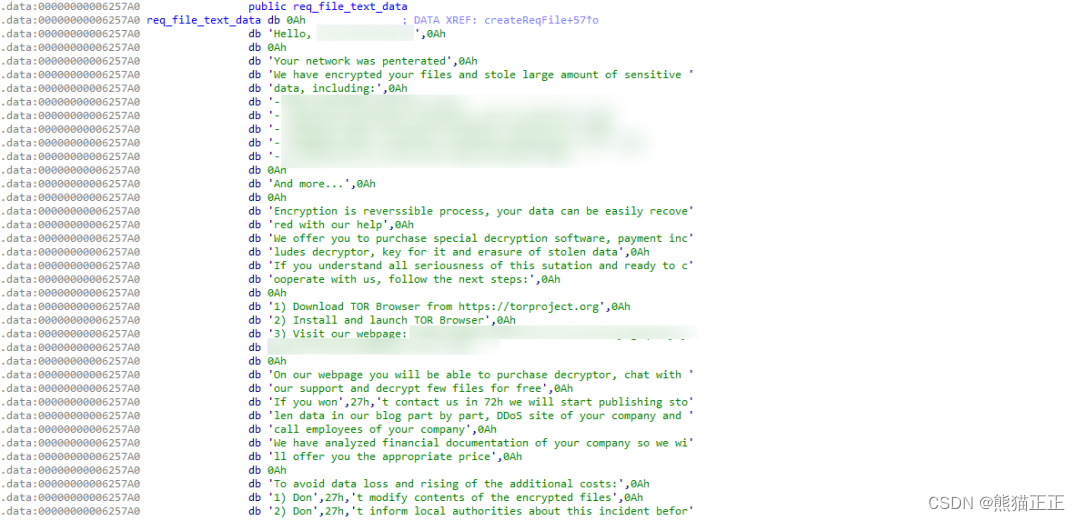
新型RedAlert勒索病毒针对VMWare ESXi服务器
前言 RedAlert勒索病毒又称为N13V勒索病毒,是一款2022年新型的勒索病毒,最早于2022年7月被首次曝光,主要针对Windows和Linux VMWare ESXi服务器进行加密攻击,到目前为止该勒索病毒黑客组织在其暗网网站上公布了一名受害者&#x…...

qt-C++笔记之判断一个QLabel上有没有load图片
qt-C笔记之判断一个QLabel上有没有load图片 code review! 在Qt框架中,QLabel是用来显示文本或者图片的一个控件。如果你想判断一个QLabel控件上是否加载了图片,你可以检查它的pixmap属性。pixmap属性会返回一个QPixmap对象,如果没有图片被加…...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Menu组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Menu组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、Menu组件 以垂直列表形式显示的菜单。 子组件 包含MenuItem、MenuItemGroup子组…...

vue三种路由守卫详解
在 Vue 中,可以通过路由守卫来实现路由鉴权。Vue 提供了三种路由守卫:全局前置守卫、全局解析守卫和组件内的守卫。 全局前置守卫 通过 router.beforeEach() 方法实现,可以在路由跳转之前进行权限判断。在这个守卫中,可以根据用…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
