解线性方程组(二)——Jacobi迭代法求解(C++)
迭代法
相比于直接法求解,迭代法使用多次迭代来逐渐逼近解,其精度比不上直接法,但是其速度会比直接法快很多,计算精度可控,特别适用于求解系数矩阵为大型稀疏矩阵的方程组。
Jacobi迭代法
假设有方程组如下:
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ ⋯ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n \begin{cases} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2\\ \cdots \qquad \qquad\cdots \qquad \qquad \cdots \\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n\\ \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯an1x1+an2x2+⋯+annxn=bn
将其转换为矩阵形式
A x ⃗ = b ⃗ A\vec{x}=\vec{b} Ax=b
[ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [ x 1 x 2 ⋮ x n ] = [ b 1 b 2 ⋮ b n ] \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\ \end{bmatrix} \begin{bmatrix} {x_{1}}\\ {x_{2}}\\ {\vdots}\\ {x_{n}}\\ \end{bmatrix}= \begin{bmatrix} {b_{1}}\\ {b_{2}}\\ {\vdots}\\ {b_n} \end{bmatrix} a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn x1x2⋮xn = b1b2⋮bn
对于是否可以使用Jacobi迭代法,需要满足以下条件之一:
- A为行对角优阵,即 ∣ a i i ∣ > ∑ j ≠ i ∣ a i j ∣ ( i = 1 , 2 , ⋯ , n ) |a_{ii}|>\sum_{j \neq i}|a_{ij}|(i=1,2,\cdots,n) ∣aii∣>∑j=i∣aij∣(i=1,2,⋯,n)
- A为行列角优阵,即 ∣ a j j ∣ > ∑ j ≠ i ∣ a i j ∣ ( j = 1 , 2 , ⋯ , n ) |a_{jj}|>\sum_{j \neq i}|a_{ij}|(j=1,2,\cdots,n) ∣ajj∣>∑j=i∣aij∣(j=1,2,⋯,n)
- A的元素满足 ∑ i ≠ j ∣ a i j ∣ ∣ a i i ∣ < 1 ( j , 1 , 2 , ⋯ , n ) \sum_{i \neq j}\frac{|a_{ij}|}{|aii|}<1(j,1,2,\cdots,n) ∑i=j∣aii∣∣aij∣<1(j,1,2,⋯,n)
若矩阵A满足上述条件之一,则可以使用Jacobi迭代法求解方程组。
首先将上述的方程组转为如下形式:
{ x 1 = 1 a 11 ( − a 12 x 2 − ⋯ − a 1 n x n + b 1 ) x 2 = 1 a 22 ( − a 21 x 1 − ⋯ − a 2 n x n + b 2 ) ⋯ ⋯ ⋯ x n = 1 a n n ( − a n 1 x 1 − ⋯ − a n n − 1 x n − 1 + b n ) \begin{cases} x_1=\frac{1}{a_{11}}(-a_{12}x_2-\cdots -a_{1n}x_n+b_1)\\ x_2=\frac{1}{a_{22}}(-a_{21}x_1-\cdots -a_{2n}x_n+b_2)\\ \cdots \qquad \qquad\cdots \qquad \qquad \cdots \\ x_n=\frac{1}{a_{nn}}(-a_{n1}x_1-\cdots -a_{nn-1}x_{n-1}+b_n)\\ \end{cases} ⎩ ⎨ ⎧x1=a111(−a12x2−⋯−a1nxn+b1)x2=a221(−a21x1−⋯−a2nxn+b2)⋯⋯⋯xn=ann1(−an1x1−⋯−ann−1xn−1+bn)
写成矩阵形式可以得到Jacobi迭代式:
( D + L + u ) x ⃗ = b ⃗ D x ⃗ = − ( L + U ) x ⃗ + b ⃗ x ⃗ ( k + 1 ) = − D − 1 ( L + U ) x ⃗ ( k ) + D − 1 b ⃗ (D+L+u)\vec{x}=\vec{b}\\ D\vec{x}=-(L+U)\vec{x}+\vec{b}\\ \vec{x}^{(k+1)}=-D^{-1}(L+U)\vec{x}^{(k)}+D^{-1}\vec{b} (D+L+u)x=bDx=−(L+U)x+bx(k+1)=−D−1(L+U)x(k)+D−1b
其中 D D D为对角矩阵, L L L为下三角矩阵- D D D, U U U为上三角矩阵- U U U, D + L + U D+L+U D+L+U为矩阵A。

代码实现
由于这个过程涉及大量的矩阵操作,整个算法分为两个源文件:Matrix.cpp实现矩阵操作,main.cpp实现Jacobi迭代法。
首先是Matrix.cpp的代码,其中矩阵求逆的原理参考:
#include <Matrix.h>
#include <iostream>
#include <cmath>
//矩阵与向量相乘,输入矩阵A,向量b,运算结果result和维数n
void matrix_multiply_vector(double **A,double *b,double * result,int n)
{for(int i=0;i<n;i++){result[i]=0.0;for(int j=0;j<n;j++){result[i]+=A[i][j]*b[j];}}
}
//矩阵乘法
void matrix_multiply_matrix(double **A,double **B,double **result,int n)
{for(int i=0;i<n;i++){for(int j=0;j<n;j++){result[i][j]=0.0;for(int k=0;k<n;k++){result[i][j]+=A[i][k]*B[k][j];}}}
}
//矩阵加减法
void matrix_add_matrix(double **A,double **B,double **result,int n,bool isAdd)
{for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(isAdd){result[i][j]=A[i][j]+B[i][j];}else{result[i][j]=A[i][j]-B[i][j];}}}
}
//向量的加减法
void vactor_add_vector(double *A,double *B,double *result,int n,bool isAdd)
{for(int i=0;i<n;i++){if(isAdd){result[i]=A[i]+B[i];}else{result[i]=A[i]-B[i];}}
}
//判断向量误差范围,只要符合精度即可
bool vector_equal(double *A,double *B,int n,double error)
{for(int i=0;i<n;i++){if(fabs(A[i]-B[i])>error){return false;}}return true;
}
//向量赋值
void vector_copy(double *A,double *B,int n)
{for(int i=0;i<n;i++){B[i]=A[i];}
}
//矩阵初始化
void matrix_init(double **A,int n)
{for(int i=0;i<n;i++){A[i]=new double [n];for(int j=0;j<n;j++){A[i][j]=0.0;}}
}
//判断矩阵A是否有收敛性
bool astringency(double **A,int n)
{double abs_row_sum=0.0;double abs_col_sum=0.0;double the_third_condition=0.0;bool RowOptimalMatrix=true;bool ColOptimalMatrix=true;for(int i=0;i<n;i++)//判断是不是行对角优阵{abs_row_sum=0.0;for(int j=0;j<n;j++){if(i!=j){abs_row_sum+=fabs(A[i][j]);}}if(abs_row_sum>A[i][i])//证明不是行对角优阵{RowOptimalMatrix=false;break;}}for(int j=0;j<n;j++)//判断是不是列对角优阵{abs_col_sum=0.0;for(int i=0;i<n;i++){if(i!=j){abs_col_sum+=fabs(A[i][j]);}}if(abs_col_sum>A[j][j]){ColOptimalMatrix=false;break;}}return ColOptimalMatrix or RowOptimalMatrix;
}
//矩阵交换某两行
void matrix_swap_row(double **A,int i,int j,int n)
{double temp;for(int k=0;k<n;k++){temp=A[i][k];A[i][k]=A[j][k];A[j][k]=temp;}
}
//矩阵第i行=矩阵第i行-矩阵第j行*a
void matrix_minus_inner(double **A,double a,int i,int j,int n)
{for(int k=0;k<n;k++){A[i][k]-=a*A[j][k];}
}
//矩阵求逆
void matrix_inverse(double **A,double **A_inverse,int n)
{double **A_E=new double*[2*n];//构建增广矩阵for(int i=0;i<n;i++){A_E[i]=new double [n*2];for(int j=0;j<n*2;j++){if(j<n){A_E[i][j]=A[i][j];}else if((j-n)==i){A_E[i][j]=1;}else{A_E[i][j]=0;}}}//首先将矩阵化为上三角矩阵for(int i=0;i<n;i++){if(A_E[i][i]==0){for(int k=i+1;k<n;k++){if(A_E[k][i]!=0){matrix_swap_row(A_E,i,k,n*2);break;}}}for(int j=i+1;j<n;j++){matrix_minus_inner(A_E,A_E[j][i]/A_E[i][i],j,i,2*n);}}//判断矩阵是否可逆for(int i=0;i<n;i++){if(A_E[i][i]==0){std::cout<<"矩阵不可逆"<<std::endl;exit(0);}}//将上三角转换为对角矩阵for(int j=1;j<n;j++){for(int i=0;i<j;i++){matrix_minus_inner(A_E,A_E[i][j]/A_E[j][j],i,j,2*n);}}for(int i=0;i<n;i++){for(int j=n;j<2*n;j++){A_inverse[i][j-n]=A_E[i][j]/A_E[i][i];}}
}
main.cpp文件内容如下:
//Jacobi迭代法求解线性方程组
/*
5x1+2x2-2x3=1
x1+4x2+x3=2
x1-2x2+4x3=-1
*/
#include<iostream>
#include<cmath>
#include<Matrix.h>//自定义头文件
using namespace std;
int main()
{int n;cout<<"Enter the matrix dimension A: ";cin>>n;//输入数组维度double **A=new double *[n];cout<<"Enter the coefficient matrix:"<<endl;for(int i=0;i<n;i++){A[i]=new double[n];for(int j=0;j<n;j++){cin>>A[i][j];//每次输入一个数字都用空格隔开,输入样例//1 2 3\enter//4 5 6\enter//7 8 9\enter}}double *b=new double[n];cout<<"Input vectors b: ";for(int i=0;i<n;i++){cin>>b[i];//输入方程组右边的向量,1 2 3\enter}bool isAstringency=astringency(A,n);//判断系数矩阵A是否具有收敛性if(isAstringency){cout<<"矩阵A符合收敛性"<<endl;}else{exit(0);cout<<"矩阵A不符合收敛性"<<endl;}double *x=new double[n];//解向量Xdouble *x_last=new double[n];//上一次的xfor(int i=0;i<n;i++){x[i]=0.0;//初始化x}double **A_L_U=new double*[n];//L+Udouble **A_D_inverse=new double*[n];//D的逆for(int i=0;i<n;i++){A_D_inverse[i]=new double [n];A_L_U[i]=new double [n];for(int j=0;j<n;j++){if(i==j){A_L_U[i][j]=0.0;A_D_inverse[i][j]=1.0/A[i][j];//对角矩阵的逆为其倒数}else{A_L_U[i][j]=A[i][j];A_D_inverse[i][j]=0.0;}}}double **B=new double *[n];//公式前半段的矩阵matrix_init(B,n);matrix_multiply_matrix(A_D_inverse,A_L_U,B,n);//求D^(-1)(L+U)double *f=new double[n];matrix_multiply_vector(A_D_inverse,b,f,n);//求取D^-1 * bdouble *temp1=new double[n];do{vector_copy(x,x_last,n);matrix_multiply_vector(B,x_last,temp1,n);//计算公式前半段vactor_add_vector(f,temp1,x,n,false);}while(vector_equal(x,x_last,n,1e-6)==false);//判断向量在误差范围内相等cout<<"运行结果为:"<<endl;for(int i=0;i<n;i++){cout<<x[i]<<" ";}system("pause");return 0;
}
结果分析
代码运行结果如下:

当下一次的迭代结果与上一次的迭代结果的最大相差值小于1e-6时,认为迭代已经收敛,输出结果即可(当然也可以换成其它结束迭代方法,如:判断两个向量之差的二范数)。
与直接使用克拉默法则计算准确的解以及matlab计算结果比较,不难发现其 x 1 x_1 x1和 x 3 x_3 x3均不为0,只是是一个在我们设定的误差范围内接近0的数,符合迭代法的解的性质,只能在设定的误差范围内得到一个近似的解。
相关文章:

解线性方程组(二)——Jacobi迭代法求解(C++)
迭代法 相比于直接法求解,迭代法使用多次迭代来逐渐逼近解,其精度比不上直接法,但是其速度会比直接法快很多,计算精度可控,特别适用于求解系数矩阵为大型稀疏矩阵的方程组。 Jacobi迭代法 假设有方程组如下…...
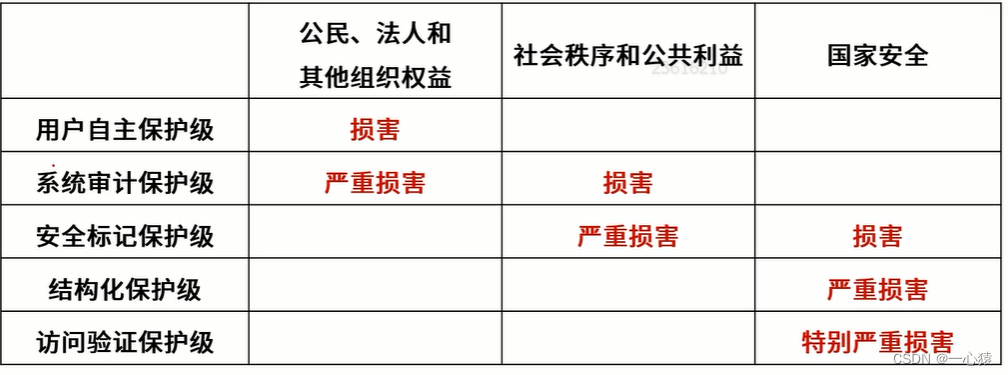
信息安全技术基础知识
一、考点分布 信息安全基础(※※)信息加密解密技术(※※※)密钥管理技术(※※)访问控制及数字签名技术(※※※)信息安全的保障体系 二、信息安全基础 信息安全包括5个基本要素&#…...

使用Taro开发鸿蒙原生应用——快速上手,鸿蒙应用开发指南
导读 本指南为开发者提供了使用 Taro 框架开发鸿蒙原生应用的快速入门方法。Taro,作为一个多端统一开发框架,让开发者能够使用一套代码同时适配多个平台,包括鸿蒙系统。文章将详细介绍如何配置开发环境,以及如何利用 Taro 的特性…...

C语言指针(初阶)
文章目录 1:内存与地址1.1内存1.2:如何理解编址 2:指针变量与地址2.1:指针变量与解引用操作符2.1.1:指针变量2.1.2:如何拆解指针类型2.1.3:解引用操作符 2.2:指针变量的大小 3:指针变量类型的意义代码1解引用修改前解引用修改后 代码2解引用修改前解引用修改后 4:const修饰指针…...

Python循环语句——for循环的嵌套使用
一、引言 在Python编程中,循环是控制程序流程的重要工具,它允许我们重复执行某段代码,直到满足特定的条件为止。其中,for循环是Python中最常用的循环类型之一。而嵌套循环,即在一个循环内部再嵌套另一个循环ÿ…...

Java创建线程真的有三种方式吗?
(/≧▽≦)/~┴┴ 嗨~我叫小奥 ✨✨✨ 👀👀👀 个人博客:小奥的博客 👍👍👍:个人CSDN ⭐️⭐️⭐️:传送门 🍹 本人24应届生一枚,技术和水平有限&am…...

17-k8s控制器资源-job控制
job控制器:就是一次性任务的pod控制器,pod完成作业后不会重启,其重启策略是:Never 1,job控制器案例描述 启动一个pod,执行完成一个事件,然后pod关闭; 事件:计算π的值&a…...
lazarus:LCL 嵌入 fpwebview 组件,做一个简单浏览器
从 https://github.com/PierceNg/fpwebview 下载 fpwebview-master.zip 简单易用。 先请看 \fpwebview-master\README.md cd \lazarus\projects\fpwebview-master\demo\lclembed 修改 lclembed.lpr 如下,将 fphttpapp. 注释掉,因为我用不上 a simple…...
c++类和对象新手保姆级上手教学(上)
前言: c其实顾名思义就是c语言的升级版,很多刚学c的同学第一感觉就是比c语言难学很多,其实没错,c里的知识更加难以理解可以说杂且抽象,光是类和对象,看起来容易,但想完全吃透,真的挺…...

可变参数(c/c++)
目录 一、C语言版本 二、C的实现方法 2.1数据包 2.2sizeof...运算符 2.3可变参数模板的使用 2.4emplace_back() 有时候我们在编写函数时,可能不知道要传入的参数个数,类型 。比如我们要实现一个叠加函数,再比如c语言中的printf,c中的emp…...

【数据结构】图
文章目录 图1.图的两种存储结构2.图的两种遍历方式3.最小生成树的两种算法(无向连通图一定有最小生成树)4.单源最短路径的两种算法5.多源最短路径 图 1.图的两种存储结构 1. 图这种数据结构相信大家都不陌生,实际上图就是另一种多叉树&…...
32.3K Star,再见 Postman,这款开源 API 客户端更香
Hi,骚年,我是大 G,公众号「GitHub指北」会推荐 GitHub 上有趣有用的项目,一分钟 get 一个优秀的开源项目,挖掘开源的价值,欢迎关注。 使用 API 工具来调试接口是后端开发经常会使用的,之前一直…...

Python循环语句——continue和break
一、引言 在Python编程中,循环是常见的控制流语句,它允许我们重复执行一段代码,直到满足某个条件为止。而在循环中,continue和break是两个非常重要的控制语句,它们可以帮助我们更加灵活地控制循环的行为。 二、contin…...

C++面向对象程序设计-北京大学-郭炜【课程笔记(三)】
C面向对象程序设计-北京大学-郭炜【课程笔记(三)】 1、构造函数(constructor)1.1、基本概念 2、赋值构造函数2.1、基本概念2.1、复制构造函数起作用的三种情况2.2、常引用参数的使用 3、类型转换构造函数3.1、什么事类型转换构造函…...
Linux:搭建docker私有仓库(registry)
当我们内部需要存储镜像时候,官方提供了registry搭建好直接用,废话少说直接操作 1.下载安装docker 在 Linux 上安装 Docker Desktop |Docker 文档https://docs.docker.com/desktop/install/linux-install/安装 Docker 引擎 |Docker 文档https://docs.do…...

用HTML、CSS和JS打造绚丽的雪花飘落效果
目录 一、程序代码 二、代码原理 三、运行效果 一、程序代码 <!DOCTYPE html> <html><head><meta http-equiv"Content-Type" content"text/html; charsetGBK"><style>* {margin: 0;padding: 0;}#box {width: 100vw;heig…...

订餐|网上订餐系统|基于springboot的网上订餐系统设计与实现(源码+数据库+文档)
网上订餐系统目录 目录 基于springboot的网上订餐系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户功能模块的实现 (1)用户注册界面 (2)用户登录界面 (3)菜品详情界面 (…...

从零开始学howtoheap:解题西湖论剑Storm_note
how2heap是由shellphish团队制作的堆利用教程,介绍了多种堆利用技术,后续系列实验我们就通过这个教程来学习。环境可参见从零开始配置pwn环境:从零开始配置pwn环境:从零开始配置pwn环境:优化pwn虚拟机配置支持libc等指…...

Rust 基本环境安装
rust 基本介绍请看上一篇文章:rust 介绍 rustup 介绍 rustup 是 Rust 语言的安装器和版本管理工具。通过 rustup,可以轻松地安装 Rust 编译器(rustc)、标准库和文档。它也允许你切换不同的 Rust 版本或目标平台,以及…...
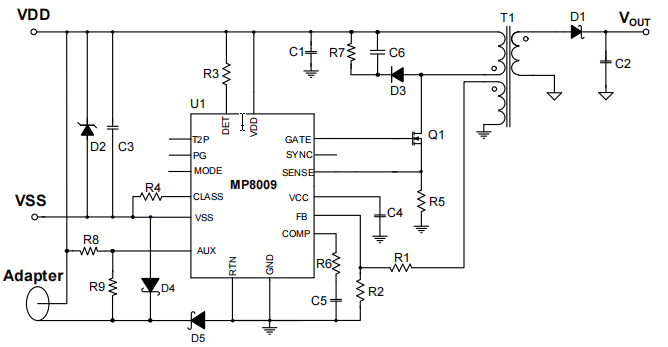
【电源】POE系统供电原理(二)
转载本博客文章,请注明出处 上一篇文章中,有提到POE系统工作原理及动态检测机制,下面我们继续介绍受电端PD技术及原理。POE供电系统包含PSE、PD及互联接口部分组成,如下图所示。 图1 POE供电系统 PSE控制器的主要作用ÿ…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
