C#,二分法(Bisection Method)求解方程的算法与源代码
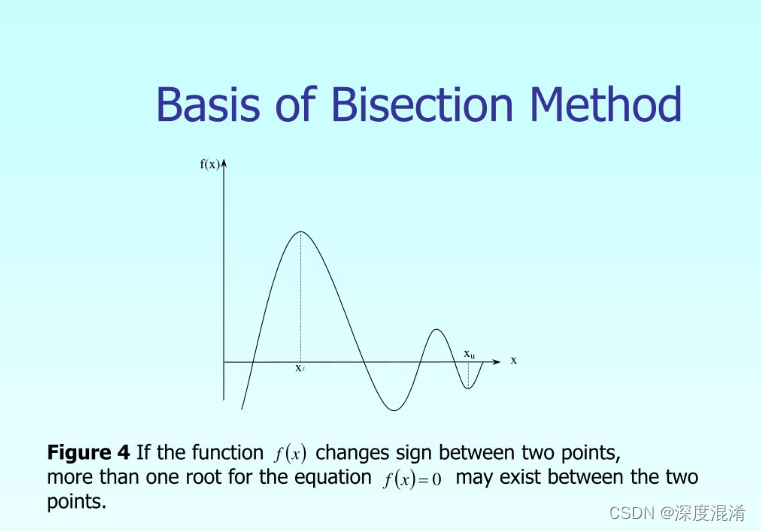
1 二分法
二分法是一种分治算法,是一种数学思维。
对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
基本思路:
给定精确度ξ,用二分法求函数f(x)零点近似值的步骤如下:
1 确定区间[a,b],验证f(a)·f(b)<0,给定精确度ξ.
2 求区间(a,b)的中点c.
3 计算f(c).
(1) 若f(c)=0,则c就是函数的零点;
(2) 若f(a)·f(c)<0,则令b=c;
(3) 若f(c)·f(b)<0,则令a=c.
(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.
2 代码
调用之前,请用委托方法给定需要求解的方程。
这样就可以求解任意的方程而无需修改核心代码。
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public delegate double delegateFunctionX(double x);public static partial class Algorithm_Gallery{public static delegateFunctionX funx = null;/// <summary>/// 二分法解方程的算法/// </summary>/// <param name="a"></param>/// <param name="b"></param>/// <param name="epsilon"></param>/// <returns></returns>public static double Bisection(double a, double b, double epsilon = 0.01){if (funx(a) * funx(b) >= 0){return 0.0;}double c = a;while ((b - a) >= epsilon){c = (a + b) / 2;if (funx(c) == 0.0){break;}else if (funx(c) * funx(a) < 0){b = c;}else{a = c;}}return c;}}
}POWER BY TRUFFER.CN
BY 315SOFT.COM
相关文章:

C#,二分法(Bisection Method)求解方程的算法与源代码
1 二分法 二分法是一种分治算法,是一种数学思维。 对于区间[a,b]上连续不断且f(a)f(b)<0的函数yf(x),通过不断地把函数f(x)的零点所在的区间…...

Portainer安装/快速上手
前置: 管理docker容器的工具 Portainer: Container Management Software for Kubernetes and Docker https://docs.portainer.io/v/ce-2.9/start/install/server/docker/linux 官网安装教程 Install Portainer CE with Docker on Linux - Portainer Documentat…...
恢复被.target勒索病毒加密的数据文件:拒绝向.target勒索病毒支付赎金
引言: 在当今数字时代,勒索病毒已成为网络安全领域的一大威胁,而.target勒索病毒是其中引起广泛关注的一种变种。本文将深入探讨.target勒索病毒的特点以及被其加密的数据文件恢复方法。数据的重要性不容小觑,您可添加我们的技术…...
【Linux网络编程六】服务器守护进程化Daemon
【Linux网络编程六】服务器守护进程化Daemon 一.背景知识:前台与后台二.相关操作三.Linux的进程间关系四.自成会话五.守护进程四步骤六.服务器守护进程化 一.背景知识:前台与后台 核心知识就是一个用户在启动Linux时,都会给一个session会话&a…...

MySQL之json数据操作
1 MySQL之JSON数据 总所周知,mysql5.7以上提供了一种新的字段格式json,大概是mysql想把非关系型和关系型数据库一口通吃,所以推出了这种非常好用的格式,这样,我们的很多基于mongoDB的业务都可以用mysql去实现了。当然…...
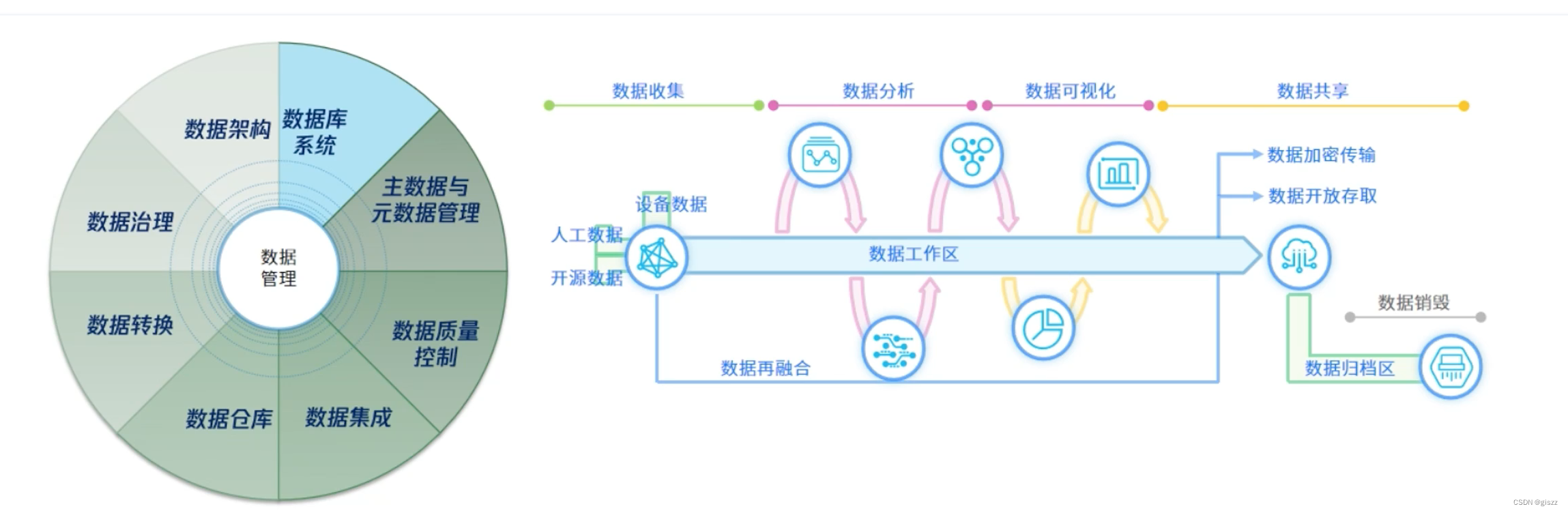
【大厂AI课学习笔记】【2.1 人工智能项目开发规划与目标】(5)数据管理
今天学习了数据管理,以及数据管理和数据治理的区别和联系。 数据管理:利用计算机硬件和软件技术对数据进行有效的收集、存储、处理和应用的过程其目的在于充分有效地发挥数据的作用。 实现数据有效管理的关键是数据组织。 数据管理和数据治理的区别&am…...

Linux满载CPU和运行内存的方法
查询CPU详细信息命令如下: 查看物理CPU型号: cat /proc/cpuinfo | grep name | cut -f2 -d: | uniq -c查看物理CPU个数 cat /proc/cpuinfo| grep "physical id"| sort| uniq| wc -l查看每个物理CPU中core的个数(即核数) cat /proc/cpuinfo…...

每日五道java面试题之java基础篇(九)
目录: 第一题 你们项⽬如何排查JVM问题第二题 ⼀个对象从加载到JVM,再到被GC清除,都经历了什么过程?第三题 怎么确定⼀个对象到底是不是垃圾?第四题 JVM有哪些垃圾回收算法?第五题 什么是STW? 第…...

spring @Transactional注解参数详解
事物注解方式: Transactional 当标于类前时, 标示类中所有方法都进行事物处理 , 例子: 1 Transactional public class TestServiceBean implements TestService {}当类中某些方法不需要事物时: Transactional public class TestServiceBean implements TestService {private…...

D - 串结构练习——字符串连接
串结构练习——字符串连接 Description 给定两个字符串string1和string2,将字符串string2连接在string1的后面,并将连接后的字符串输出。 连接后字符串长度不超过110。 Input 输入包含多组数据,每组测试数据包含两行,第一行代表s…...

什么样的服务器是高性能服务器?
首先,高性能服务器应具备高处理能力。随着业务的不断扩展和数据量的爆炸性增长,高性能服务器需要具备强大的计算能力,能够快速处理各种复杂的业务和数据。这要求高性能服务器采用先进的处理器技术,如多核处理器、GPU加速等&#x…...

数学建模【线性规划】
一、线性规划简介 线性规划通俗讲就是“有限的资源中获取最大的收益”(优化类问题)。而且所有的变量关系式都是线性的,不存在x、指数函数、对数函数、反比例函数、三角函数等。此模型要优化的就是在一组线性约束条件下,求线性目标…...

ChatGPT的大致原理
国外有个博主写了一篇博文,名字叫TChatGPT: Explained to KidsQ」, 直译过来就是,给小孩子解释什么是ChatGPT。 因为现实是很多的小孩子已经可以用父母的手机版ChatGPT玩了 ,ChatGPT几乎可以算得上无所不知,起码给小孩…...
蓝桥杯备赛_python_BFS搜索算法_刷题学习笔记
1 bfs广度优先搜索 1.1 是什么 1.2怎么实现 2案例学习 2.1.走迷宫 2.2.P1443 马的遍历 2.3. 九宫重排(看答案学的,实在写不来) 2.4.青蛙跳杯子(学完九宫重排再做bingo) 2.5. 长草 3.总结 1 bfs广度优先搜索 【P…...
)
轮播图的五种写法(原生、vue2、vue3、react类组件,react函数组件)
轮播图效果是一种在网页或应用程序中展示多张图片或内容的方式,通常以水平或垂直的方式循环播放。本文使用原生、vue2、vue3、react类组件,react函数组件五种写法实现了简单的轮播图效果,需要更多轮播效果需要再增加样式或者动画。 淡入淡出效果:每张图片渐渐淡入显示,然后…...
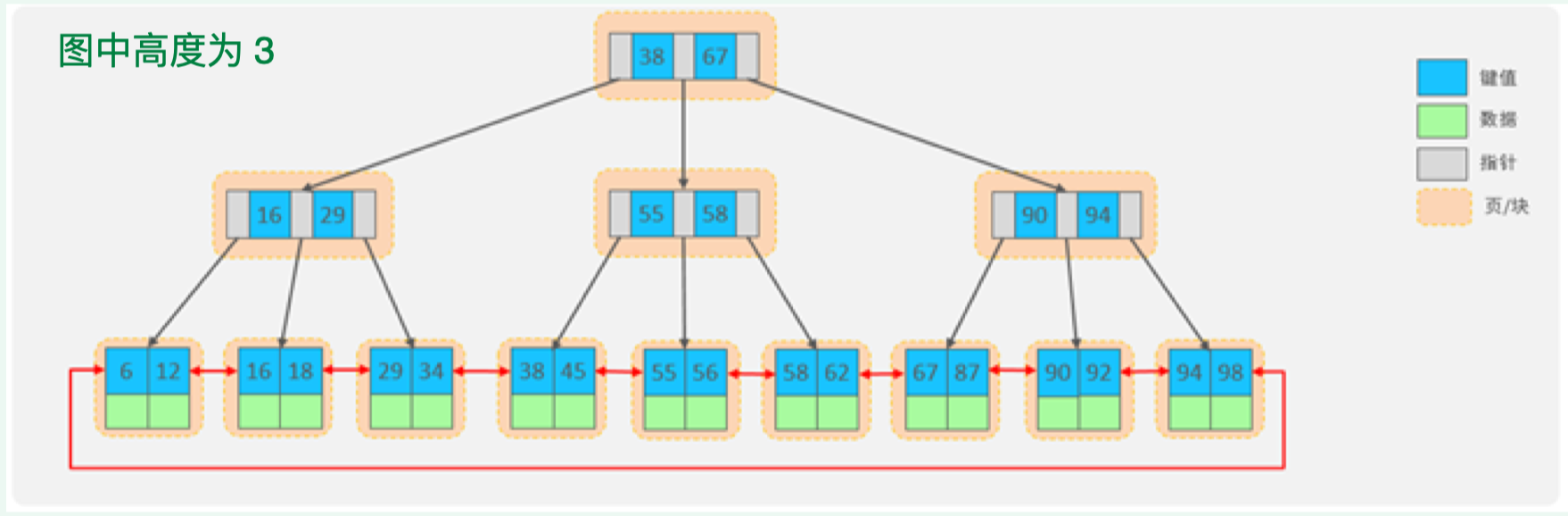
【MySQL】高度为2和3时B+树能够存储的记录数量的计算过程
文章目录 题目答案高度为2时的B树高度为3时的B树总结 GPT4 对话过程 题目 InnoDB主键索引的Btree在高度分别为 2 和 3 时,可以存储多少条记录? 答案 高度为2时的B树 计算过程: 使用公式 ( n 8 ( n 1 ) 6 16 1024 ) (n \times 8 …...
软件著作书 60页代码轻松搞定!(附exe和代码)
最近做了一个软件,准备去申请软件著作书,看着那60页的文档,确实难搞,不过幸好会用一点点python,就自己用python写了一个读取所有文件代码的程序,使用起来也很简单,过来分享一下 链接࿱…...

阿里文档类图像的智能识别,文档分类自定义分类器
阿里云文档类图像智能识别服务为用户提供了强大的文档处理能力,可以将文档图像中的文本内容、表格数据和结构化信息自动识别并提取出来。而自定义分类器则允许用户根据自己的需求,训练出更适合自己场景的文档分类模型。本文将详细介绍阿里云文档类图像智…...
)
256.【华为OD机试真题】会议室占用时间(区间合并算法-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目二.解题思路三.题解代码Python题解代码JAVA题解…...
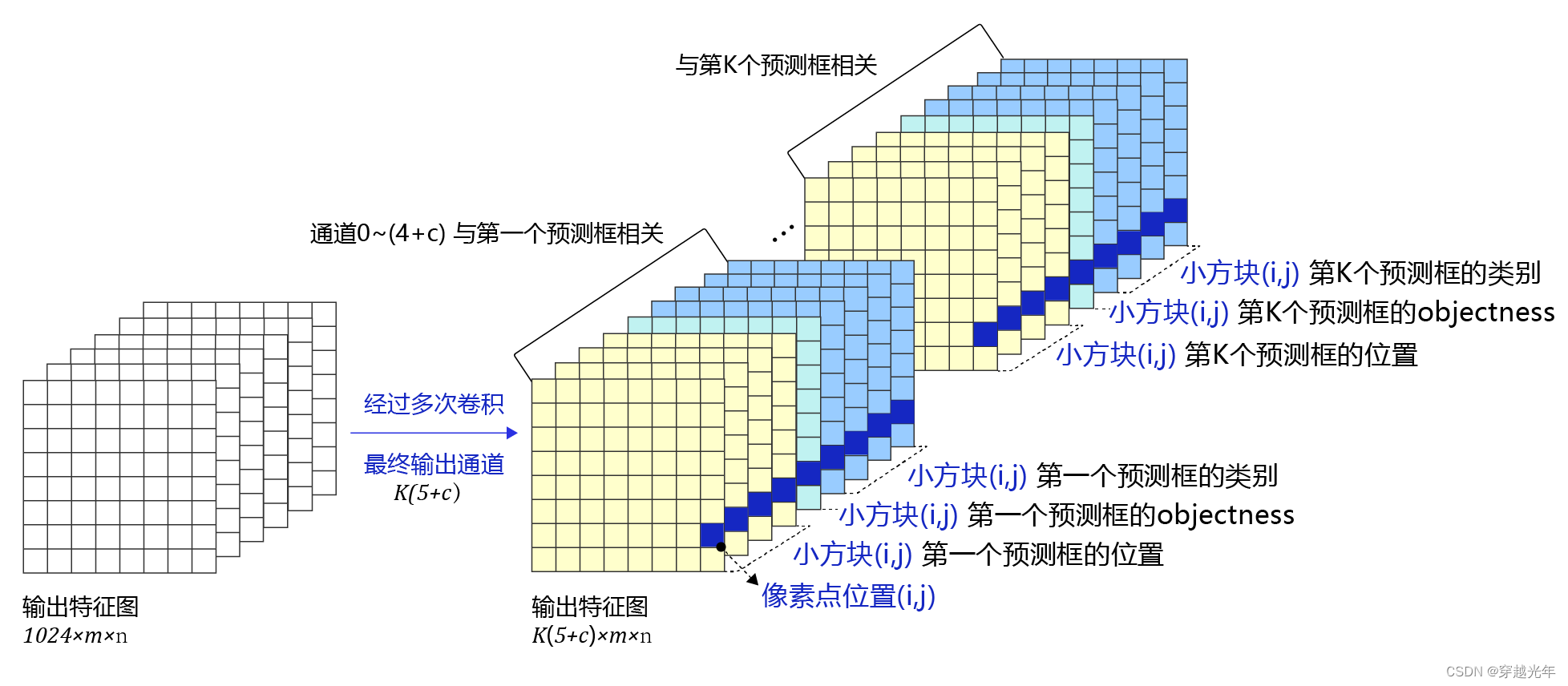
人工智能学习与实训笔记(三):神经网络之目标检测问题
人工智能专栏文章汇总:人工智能学习专栏文章汇总-CSDN博客 目录 三、目标检测问题 3.1 目标检测基础概念 3.1.1 边界框(bounding box) 3.1.2 锚框(Anchor box) 3.1.3 交并比 3.2 单阶段目标检测模型YOLOv3 3.2…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
