债券专题二:可转债估值-二叉树模型
1. 模型背景
由于可转债自身的属性较多,因此对其定价的难度也会加大,在诸多影响因素中,未来的股价占比最高。由于股价的不可预测性,导致了可转债的定价在实际交易中作用非常有限。随着可转债发行数量和规模的增大,越来越多的机构参与到其中,这也使得越来越多的人开始研究可转债定价,可转债的投机属性降低。随着量化投资的火爆,越来越多的可转债影响因素被标准化,推动了可转债模型定价的迭代的发展。基于市场扩容和技术进步,可转债定价有效性在逐渐加大。目前常见的可转债估值模型有3种:BS模型,二叉树模型,蒙特卡罗模型。本文主要分享二叉树模型的估值逻辑,并复现其代码。
2. 模型公式


3. 模型代码
import numpy as npclass Convertible_Bond(object):def __init__(self, T, vol, market, st, rate, r, coupon, r_, dt, up, down, lp):self.T = T # 期限self.vol = vol # 波动率self.market = market # 面值self.st = st # 股票价格self.rate = rate # 转换比率self.r = r # 无风险利率self.coupon = coupon # 票息self.r_ = r_ # 信用利差self.dt = dt # 赎回间隔self.up = up # 上涨空间self.down = down # 下跌空间self.lp = lp # 赎回价格# 计算风险中性概率def risk_p(self):a = np.e ** (self.r * self.dt)return (a - self.down) / (self.up - self.down)# 计算到期价值def expire_value(self, expire_price):# expire_price:到期股票价格# 计算到期转换价值change_value = expire_price * self.rate + self.market * self.coupon# 计算含票息的价值coupon_value = self.market * (1 + self.coupon)V = max(change_value, coupon_value)return V# 计算每一个节点的连续价值def continuous_value(self, expire_up, expire_down):# expire_down:下一节点下跌对应的可转债到期价值# expire_up:下一节点上涨对应的可转债到期价值b = np.e ** (-(self.r + self.r_) * self.dt)risk_p = self.risk_p()coupon_v = self.market * self.couponH = b * (risk_p * expire_up + (1 - risk_p) * expire_down) + coupon_vreturn H# 计算当前的节点价值def really_value(self, expire_price, H):# 计算提前兑付值,假设在赎回时获得票息收入C = self.market * self.couponK = self.market + CV = max(self.rate * expire_price + C, min(H, K))return V4. 模型实例
某可赎回可转债要素如下:(为简化起见,模型暂不考虑部分可转债的特性,使用两步长的最基础的可转债作为案例。)
| 可赎回-可转债要素 | |||
| 期限 | 2年 | 波动率 | 20% |
| 面值 | 100 | 股票价格 | 100 |
| 转换比例 | 0.8 | 利率 | 3% |
| 票息率 | 3% | 信用利差 | 1% |
| 赎回条款 | 只在第一年 | 上涨比例 | 1.2214 |
| 赎回价格 | 100 | 下跌比例 | 0.8187 |
首先,对函数进行传参,同时计算s1到s5的值:
if __name__ == '__main__':T, vol, market, st, rate, r = 2, 0.2, 100, 100, 0.8, 0.03coupon, r_, dt, up, down, lp = 0.03, 0.01, 1, 1.2214, 0.8187, 100model = Convertible_Bond( T, vol, market, st, rate,r, coupon, r_, dt, up, down, lp)# 分别计算股票s1,到s5的值s1 = round(st*up,2)s2 = round(st*down,2)s3 = round(s1*up,2)s4 = round(s1*down,2)s5 = round(s2*down,2)计算得到的结果为:
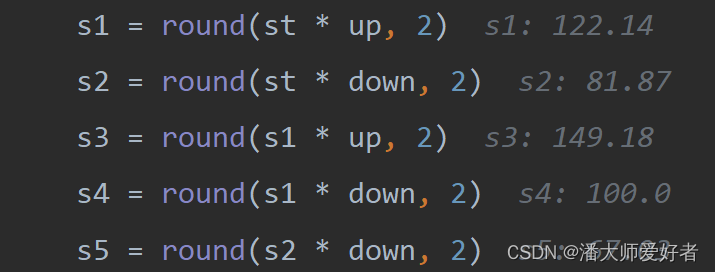
然后,根据 s3,s4,s5的值可以计算出对应节点债券的到期价值:

接下来,根据b3到b5的到期价值,计算b1,b2节点上的连续价值H1,H2:
 随后,考虑可赎回性,根据s1,s2和H1,H2,计算b1,b2节点上的 节点价值1,V2:
随后,考虑可赎回性,根据s1,s2和H1,H2,计算b1,b2节点上的 节点价值1,V2:

紧接着,使用V1和V2的 值计算当前节点的连续价值H,根据H和s1计算当前节点可赎回债券的估值V:

本章节的完整代码为:
if __name__ == '__main__':T, vol, market, st, rate, r = 2, 0.2, 100, 100, 0.8, 0.03coupon, r_, dt, up, down, lp = 0.03, 0.01, 1, 1.2214, 0.8187, 100model = Convertible_Bond(T, vol, market, st, rate,r, coupon, r_, dt, up, down, lp)# 分别计算股票s1,到s5的值s1 = round(st * up, 2)s2 = round(st * down, 2)s3 = round(s1 * up, 2)s4 = round(s1 * down, 2)s5 = round(s2 * down, 2)# 计算债券b3,b4,b5的值b3 = round(model.expire_value(s3), 2)b4 = round(model.expire_value(s4), 2)b5 = round(model.expire_value(s5), 2)# 计算H1和H2的值H1 = round(model.continuous_value(b3, b4), 2)H2 = round(model.continuous_value(b4, b5), 2)# 计算b1,b2节点上的节点价值V1 = model.really_value(s1, H1)V2 = model.really_value(s2, H2)# 计算当前节点的连续价值HH = round(model.continuous_value(V1, V2), 2)# 计算当前节点可转债的估值V = model.really_value(st, H)本期分享结束,有何问题欢迎随时交流。
相关文章:

债券专题二:可转债估值-二叉树模型
1. 模型背景 由于可转债自身的属性较多,因此对其定价的难度也会加大,在诸多影响因素中,未来的股价占比最高。由于股价的不可预测性,导致了可转债的定价在实际交易中作用非常有限。随着可转债发行数量和规模的增大,越…...

【闲谈】开源软件的崛起与影响
随着信息技术的快速发展,开源软件已经成为软件开发的趋势,并产生了深远的影响。开源软件的低成本、可协作性和透明度等特点,使得越来越多的企业和个人选择使用开源软件,促进了软件行业的繁荣。然而,在使用开源软件的过…...
【教程】Linux使用aria2c多线程满速下载
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 安装aria2c: sudo apt-get install aria2多线程下载: aria2c -x 16 -s 16 <url> 比如: aria2c -x 16 -s 16 http://images.cocodataset.org/zips/test2017.zip...
【漏洞复现】蓝网科技临床浏览系统信息泄露漏洞
Nx01 产品简介 蓝网科技临床浏览系统是一个专门用于医疗行业的软件系统,主要用于医生、护士和其他医疗专业人员在临床工作中进行信息浏览、查询和管理。 Nx02 漏洞描述 蓝网科技临床浏览系统存在信息泄露漏洞,攻击者可以利用该漏洞获取敏感信息。 Nx03…...

JSON转换List<Map<String, Object>>、Map<String, Object>
废话就不说了 早上10点研究到现在 获取redis的JSON字符串 String getPalletListNew redisService.getRedis(“getPalletListNew”, abroad “” goodsLevel “” startPort “” destinationPort “” maxTon “” minTon); 转换Map<String,Object> public …...
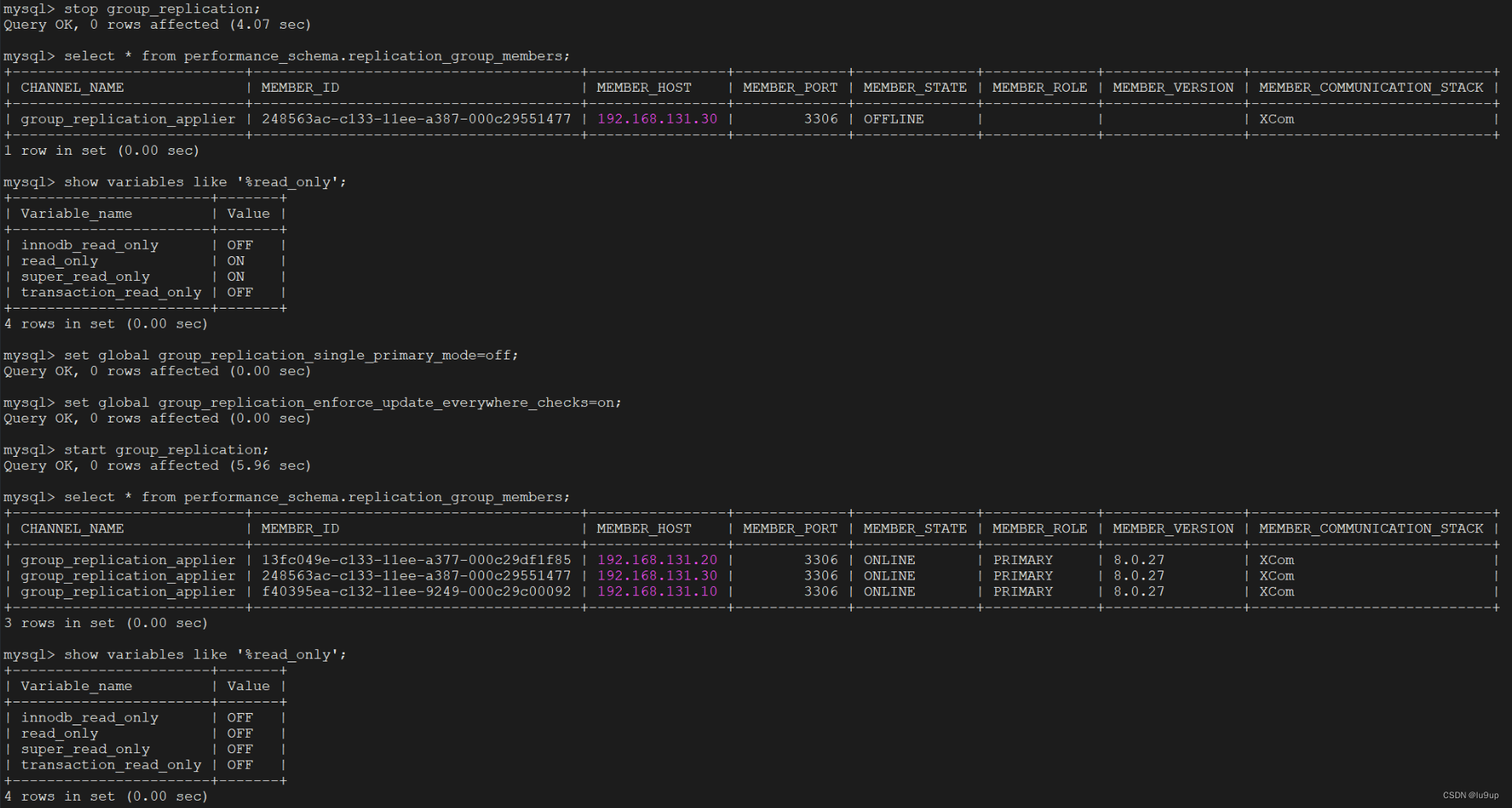
单主模式和多主模式切换
1 组复制模式切换注意点 组复制有两种运行模式,一种是单主模式,一种是多主模式。这个模式是在整个组中设置的,由 group_replication_single_primary_mode 这个系统变量指定,而且在所有成员上必须保持一致。ON 表示单主模式&#…...
petalinux2018.3安装步骤
1、虚拟机安装ubuntu-16.04.7-desktop-amd64.iso (注意:安装ubuntu-18.04.6-desktop-amd64.iso和ubuntu-16.04.6-desktop-i386.iso会报以下错误) environment: line 314: ((: 10 #15~1 > 10 #3: syntax error in expression (error toke…...
)
ubuntu22.04下使用conda安装pytorch(cpu及gpu版本)
本文介绍了conda下安装cpu、gpu版本的pytorch;并介绍了如何设置镜像源 ubuntu环境安装pytorch的CPU版本与GPU版本 系统:ubuntu22.04 显卡:RTX 3050 依赖工具:miniconda 确认环境 lsb_release -a No LSB modules are available.…...
)
突破编程_C++_高级教程(模板编程的基础知识)
1 模板编程的基本概念 C 的模板编程是一种编程技术,它允许程序员编写处理不同类型数据的通用代码。通过使用模板,可以创建与特定数据类型无关的函数或类,这些函数或类在编译时可以根据需要生成特定数据类型的版本。这增加了代码的复用性、灵…...

胆小勿入!AI创作恐怖电影宣传片《生化危机:重生》
胆小勿入!AI创作恐怖电影宣传片《生化危机:重生》 "The city is falling, and the dead walk among us." "In the shadow of the apocalypse, the fight for survival begins." "The streets are silent, but the nightmare …...
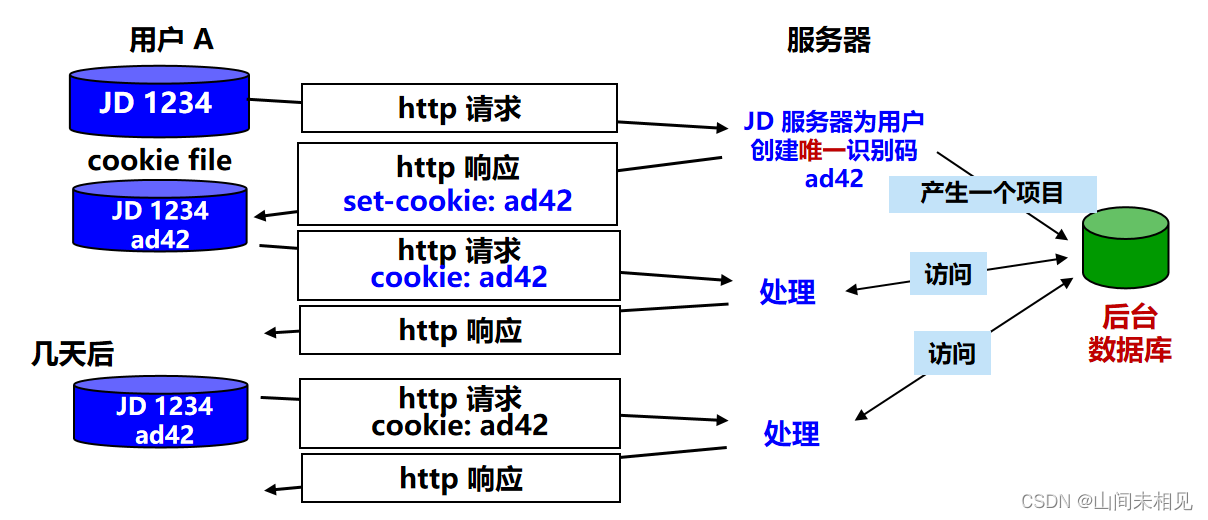
HTTP 超文本传送协议
1 超文本传送协议 HTTP HTTP 是面向事务的 (transaction-oriented) 应用层协议。 使用 TCP 连接进行可靠的传送。 定义了浏览器与万维网服务器通信的格式和规则。 是万维网上能够可靠地交换文件(包括文本、声音、图像等各种多媒体文件)的重要基础。 H…...

MySQL导入/导出数据
MySQL导入/导出数据 文章目录 MySQL导入/导出数据一、MySQL 导入数据1、mysql 命令导入2、source 命令导入3、使用 LOAD DATA 导入数据4、使用 mysqlimport 导入数据4.1、mysqlimport的常用选项介绍 二、MySQL 导出数据1、使用 SELECT ... INTO OUTFILE 语句导出数据2、mysqldu…...
Matplotlib初探:认识数据可视化与Matplotlib
Matplotlib初探:认识数据可视化与Matplotlib Fig.1 利用Matplotlib进行数据可视化( 可视化代码见文末) 🌵文章目录🌵 🌳引言🌳🌳一、数据可视化简介🌳🌳二、Matplotlib库简介&#x…...
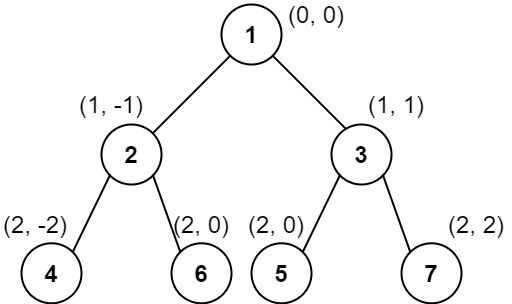
LeetCode 0987.二叉树的垂序遍历:遍历时存节点信息,遍历完自定义排序
【LetMeFly】987.二叉树的垂序遍历:遍历时存节点信息,遍历完自定义排序 力扣题目链接:https://leetcode.cn/problems/vertical-order-traversal-of-a-binary-tree/ 给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历…...

TCP 和 UDP的区别
文章目录 概述区别UDPTCPTCP与UDP的选择UDP和TCP编程区别 概述 TCP(Transmission Control Protocol,传输控制协议)和 UDP(User Datagram Protocol,用户数据报协议)是互联网中两种最常用的传输层协议 总的来…...

Python 将一维数组或矩阵变为三维
Python 将一维数组或矩阵变为三维 正文 正文 话不多说直接上代码: import numpy as npsampling_points 10001arr np.linspace(0, 2, sampling_points) arr_3D arr.reshape(1, 1, -1) print(arr_3D) """ result: [[[0.0000e00 2.0000e-04 4.0000…...
Python如何实现定时发送qq消息
因为生活中老是忘记各种事情,刚好又在学python,便突发奇想通过python实现提醒任务的功能(尽管TIM有定时功能),也可定时给好友、群、讨论组发送qq消息。其工作流程是:访问数据库提取最近计划——>根据数据…...

支付方式接入:支付宝、微信支付、微软支付
支付方式接入:支付宝、微信支付、微软支付 1、微信支付-接入指引 2、支付宝-接入指引 3、微软支付-接入指引 3.1、使用visual studio打包应用(发布到微软市场):Package a desktop app from source code using Visual Studio -…...

C++中的互斥量
互斥量是一个类,互斥量的使用必须引入头文件#include <mutex>。互斥量就如同一把锁,在同一时间,多个线程都可以调用lock成员函数尝试给这把锁头加锁,但是只有一个线程可以成功给这把锁加锁,其他没有加锁成功的线…...

盲盒小程序开发
现如今,盲盒已经成为了市场上不可忽视的新型消费模式,并且也逐渐遍布在全球各地中。盲盒的种类商品也逐渐丰富完善,不在局限于性价比高的盲盒玩具、手办等,也发展到了美妆、电子、食品等行业,具有较大的实用性和收藏价…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
