Leetcode 16-20题
最接近的三数之和
给定整数数组和目标值
target,从数组中选出三个整数,使得和与target最接近,并返回三数之和。保证恰好存在一个解。
和上一题类似,我们先对整数数组排序,然后固定i,枚举j,找到满足nums[i]+nums[j]+nums[k]>=target的最小的k。
那么显然有nums[i]+nums[j]+nums[k-1]<target,只需要判断两者谁离target最接近即可。
int threeSumClosest(vector<int>& nums, int target) {sort(nums.begin(), nums.end());int delta = INT_MAX, sum = 0;for(int i = 0; i < nums.size() - 2; i ++) {if(i && nums[i] == nums[i - 1]) continue;for(int j = i + 1, k = nums.size() - 1; j < k; j ++) {if(j > i + 1 && nums[j] == nums[j - 1]) continue;while(k - 1 > j && nums[i] + nums[j] + nums[k - 1] >= target) k --;// 找到固定i和j时满足三数之和大于等于目标值的k,可以保证i,j,k-1三数之和小于目标值int p = nums[i] + nums[j] + nums[k], q = nums[i] + nums[j] + nums[k - 1];if(abs(p - target) < delta) delta = abs(p - target), sum = p;// k-1不能和k相等if(k != j + 1 && abs(q - target) < delta) delta = abs(q - target), sum = q;}}return sum;
}
电话号码的字母组合
数字和字母的映射同电话按键,给定包含数字
2-9的字符串,返回能表示的字母组合。
这是一道非常经典的DFS题。每一层只需要枚举这一位填哪个字母,然后到头输出再返回即可。
vector<string> to = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
vector<string> ans;void dfs(string &digits, int u, string path) {if(path.size() == digits.size()) { // 若字母串和数字串相同长度则得到答案ans.push_back(path);return ;}for(auto c : to[digits[u] - '0']) { // 数字为digits[u] - '0'path += c;dfs(digits, u + 1, path); // 迭代判断第u+1个数字path.pop_back(); // 恢复现场}
}vector<string> letterCombinations(string digits) {if(!digits.size()) return ans; // 若空直接返回dfs(digits, 0, "");return ans;
}
四数之和
给定整数数组和目标值,返回四数之和等于目标值且不重复的所有四元组。
数组长度为 [ 1 , 200 ] [1,200] [1,200],数的大小为 [ − 1 0 9 , 1 0 9 ] [-10^9, 10^9] [−109,109]。
和三数之和一样,只是多了一重循环而已。
但是这里要注意,可能会爆int,判断的时候要开long long。
vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> ans;sort(nums.begin(), nums.end());for(int i = 0; i < nums.size(); i ++) {if(i && nums[i] == nums[i - 1]) continue;for(int j = i + 1; j < nums.size(); j ++) {if(j > i + 1 && nums[j] == nums[j - 1]) continue;for(int k = j + 1, l = nums.size() - 1; k < l; k ++) { // 固定i,j,kif(k > j + 1 && nums[k] == nums[k - 1]) continue;// 强转为long long来判断while(l-1 > k && 0ll + nums[i] + nums[j] + nums[k] + nums[l - 1] >= 1ll * target) l--;if(0ll + nums[i] + nums[j] + nums[k] + nums[l] == target * 1ll)ans.push_back({nums[i], nums[j], nums[k], nums[l]});}}}return ans;
}
删除链表的倒数第N个结点
删除链表的倒数第
n个结点,并且返回链表的头结点。
先扫描一边链表得到链表长度,然后再正着删除这个节点即可。可以使用虚拟头节点来取消对头节点的特判。
删除第k个节点的方法就是将第k-1个节点的next指针指向第k+1个节点。
ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* damn = new ListNode(-1, head); // 虚拟头节点int len = 0;for(auto p = head; p; p = p->next) len ++; // 原链表的长度// 1 2 3 4 5// len=5,倒数第2个是从实际头节点开始的正数第4个(len-n+1)// 倒数第n个节点就是从虚拟头节点开始正数第len - n + 2个节点// 那么从虚拟头节点要往后走len-n次才能到实际要删的节点的前面一个节点auto p = damn;for(int i = 1; i <= len - n; i ++) p = p->next;// 要删第k个节点,就将第k-1个节点的next指针指向第k+1个节点p->next = p->next->next;return damn->next;
}
有效的括号
给定只包含
()[]{}的字符串,判断是否有效。有效的标准是左右括号必须相邻且匹配。
一道经典的栈题。遇到左括号则入栈,遇到右括号则判断栈顶的左括号和当前右括号是否匹配。
最后判断栈是否为空,若栈不为空则不匹配。
左括号(的ASCII为40, 右括号)的ASCII码为41。
左括号[的ASCII为91, 右括号]的ASCII码为93。
左括号{的ASCII为123, 右括号}的ASCII码为125。
所以只要左括号和右括号的ASCII码的差的绝对值小于等于2,则可以判断匹配。
bool isValid(string s) {stack<char> st;for(auto c : s) {if(c == '(' || c == '[' || c == '{') st.push(c);else {// 一定要加abs来判断距离,否则会导致91-123=-32的情况出现if(st.size() && abs(c - st.top()) <= 2) st.pop();else return false;}}return st.empty();
}
相关文章:

Leetcode 16-20题
最接近的三数之和 给定整数数组和目标值target,从数组中选出三个整数,使得和与target最接近,并返回三数之和。保证恰好存在一个解。 和上一题类似,我们先对整数数组排序,然后固定i,枚举j,找到满…...
项目的15 个开源训练数据集)
【开源训练数据集1】神经语言程式(NLP)项目的15 个开源训练数据集
一个聊天机器人需要大量的训练数据,以便在无需人工干预的情况下快速解决用户的询问。然而,聊天机器人开发的主要瓶颈是获取现实的、面向任务的对话数据来训练这些基于机器学习的系统。 我们整理了训练聊天机器人所需的对话数据集,包括问答数据、客户支持数据、对话数据和多…...

【AIGC】Stable Diffusion的ControlNet参数入门
Stable Diffusion 中的 ControlNet 是一种用于控制图像生成过程的技术,它可以指导模型生成特定风格、内容或属性的图像。下面是关于 ControlNet 的界面参数的详细解释: 低显存模式 是一种在深度学习任务中用于处理显存受限设备的技术。在这种模式下&am…...
)
静态curl库编译与使用(c++)
静态curl库编译与使用 静态curl库编译与使用:mingw https://curl.se/windows/ // 测试:设置URL地址 // curl_easy_setopt(curlHandle, CURLOPT_URL, “https://ipinfo.io/json”); // curl_easy_setopt(curlHandle, CURLOPT_SSL_VERIFYPEER, 0L); // c…...

element 表单提交图片(表单上传图片)
文章目录 使用场景页面效果前端代码 使用场景 vue2 element 表单提交图片 1.点击【上传图片】按钮择本地图片(只能选择一张图片)后。 2.点击图片,支持放大查看。 3.点击【保存】按钮,提交表单。 页面效果 前端代码…...
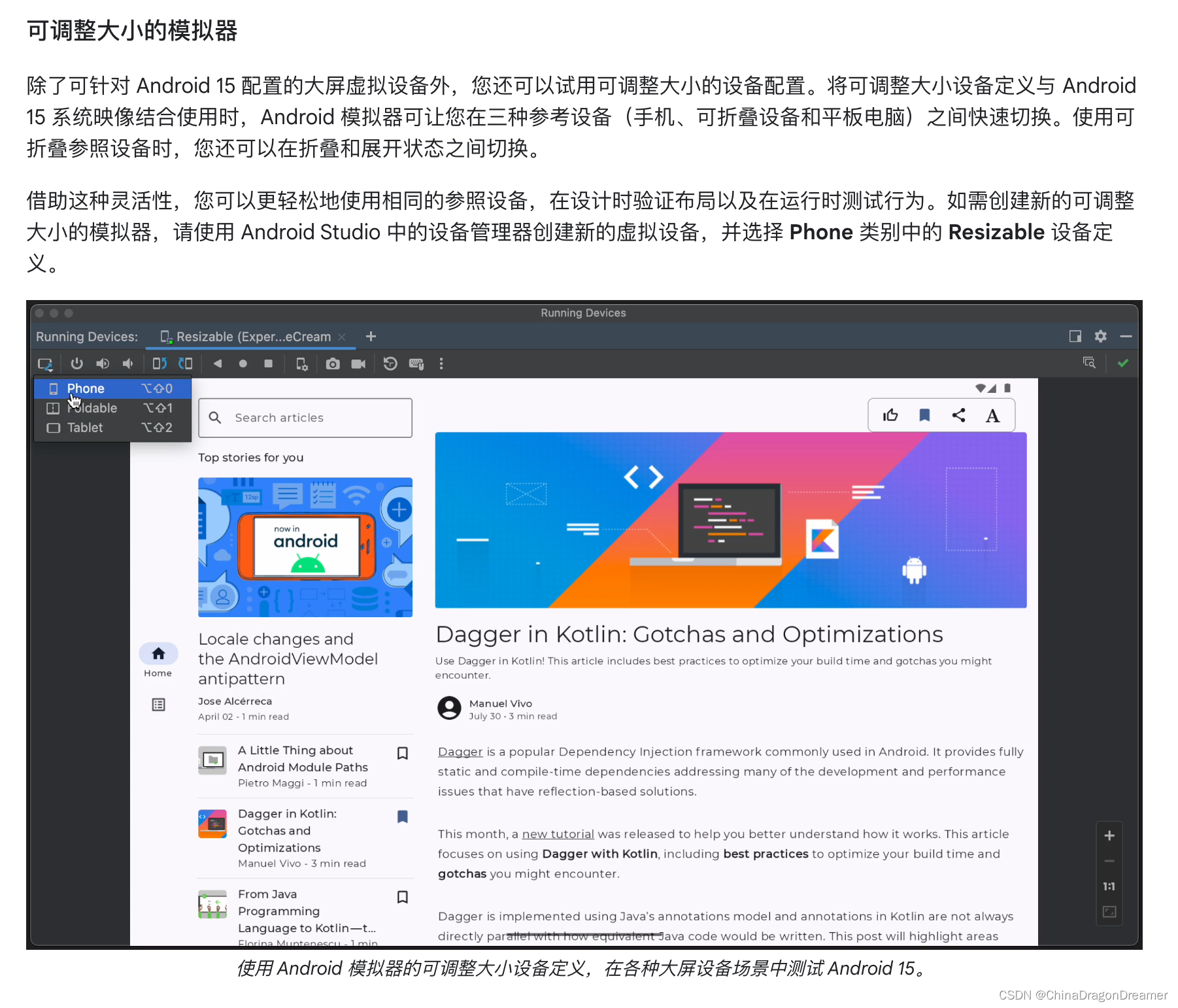
Android 15 第一个开发者预览版
点击查看:first-developer-preview-android15 点击查看:Get Android 15 2024年2月16日,谷歌发布 Android 15 第一个开发者预览版 翻译 由工程副总裁戴夫伯克发布 今天,我们发布了Android 15的首个开发者预览版,这样我们的开发者就…...
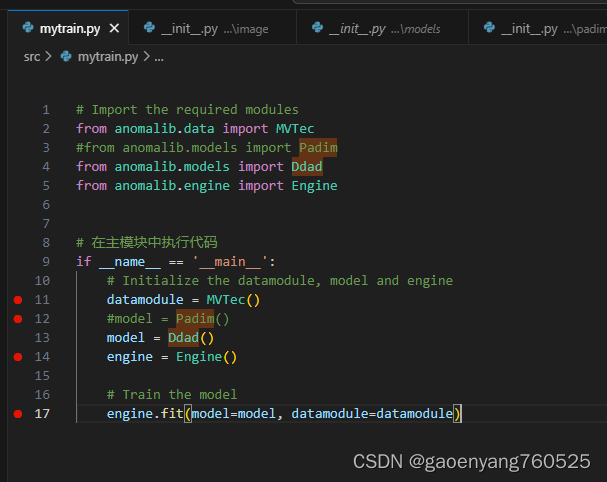
anomalib1.0学习纪实-续1:增加新算法
0、基本信息 现在我要增加一个新算法:DDAD 他的代码,可以在github中找到:GitHub - arimousa/DDAD 一、基础操作: 1、修改anomalib\src\anomalib\models\__init__.py 我增加的第33行和61行, 2、 增加ddad文件夹和文…...

Java+Vue+MySQL,国产动漫网站全栈升级
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

机器人常用传感器分类及一般性要求
机器人传感器的分类 传感技术是先进机器人的三大要素(感知、决策和动作)之一。根据用途不同,机器人传感器可以分为两大类:用于检测机器人自身状态的内部传感器和用于检测机器人相关环境参数的外部传感器。 内部传感器 内部传感…...
C++-opencv的imread、imshow、waitkey、namedWindow
在C中使用OpenCV时,imread和imshow是两个非常基础且常用的函数,用于读取图像和显示图像。以下是这两个函数的简要说明和如何一起使用它们的示例。 imread函数 imread用于从指定的文件路径读取图像。它将图像读入为cv::Mat对象,这是OpenCV中…...

开源语音识别faster-whisper部署教程
1. 资源下载 源码地址 模型下载地址: large-v3模型:https://huggingface.co/Systran/faster-whisper-large-v3/tree/main large-v2模型:https://huggingface.co/guillaumekln/faster-whisper-large-v2/tree/main large-v2模型:…...
)
使用IntelliJ IDEA配置Maven (入门)
在使用IntelliJ IDEA进行Java开发时,配置Maven是至关重要的一步,因为它可以帮助你管理项目的依赖和构建过程。以下是我在使用IntelliJ IDEA配置Maven的实践过程,以及一些技术笔记和职场感悟。 工作实践与项目复盘 下载Maven: 访问…...
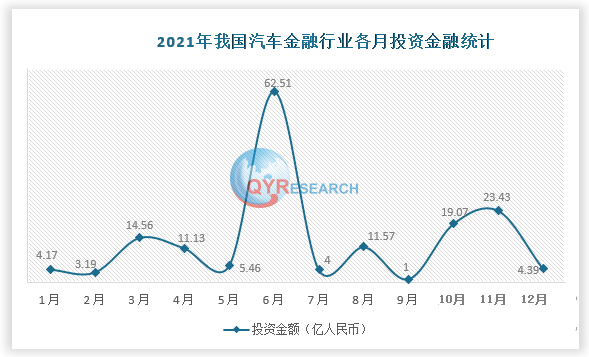
汽车金融市场研究:预计2029年将达到482亿美元
汽车金融公司作为汽车流通产业链的重要一环,认真贯彻落实国家有关政策,采取多种措施助力汽车产业发展,为促进推动汽车消费、助力畅通汽车产业链、支持稳定宏观经济大盘发挥了积极作用。 益于国内疫情得到有效控制,我国经济持续稳定…...

关于举办第十五届蓝桥杯大赛电子赛5G全网规划与建设赛项的通知
关于举办第十五届蓝桥杯大赛电子赛 5G全网规划与建设赛项的通知 各相关院校: 第十五届蓝桥杯大赛通知已于2023年9月27日在蓝桥杯大赛官网发布,现就电子赛5G全网规划与建设赛项报名事宜,公布如下: 一、赛项概述 5G全网规划与建设…...

Vue3快速上手(七) ref和reactive对比
一、ref和reactive对比 表格形式更加直观吧: 项目refreactive是否支持基本类型支持不支持是否支持对象类型支持支持对象类型是否支持属性直接赋值不支持,需要.value支持是否支持直接重新分配对象支持,因为操作的.value不支持,需…...

8、内网安全-横向移动RDPKerberos攻击SPN扫描WinRMWinRS
用途:个人学习笔记,有所借鉴,欢迎指正 目录 一、域横向移动-RDP-明文&NTLM 1.探针服务: 2.探针连接: 3.连接执行: 二、域横向移动-WinRM&WinRS-明文&NTLM 1.探针可用: 2.连接…...

《数据结构与算法之美》读书笔记
《数据结构与算法之美》读书笔记 写在前面 这本书的大部分内容比较浅显,因此只挑DSAA课程上没有涉及或没有深入讨论的点总结 第二章 数组相关 提高传统数组插入/删除数据效率的方法: 如果插入的数据不要求有序,可以直接把某位的原数据替换…...
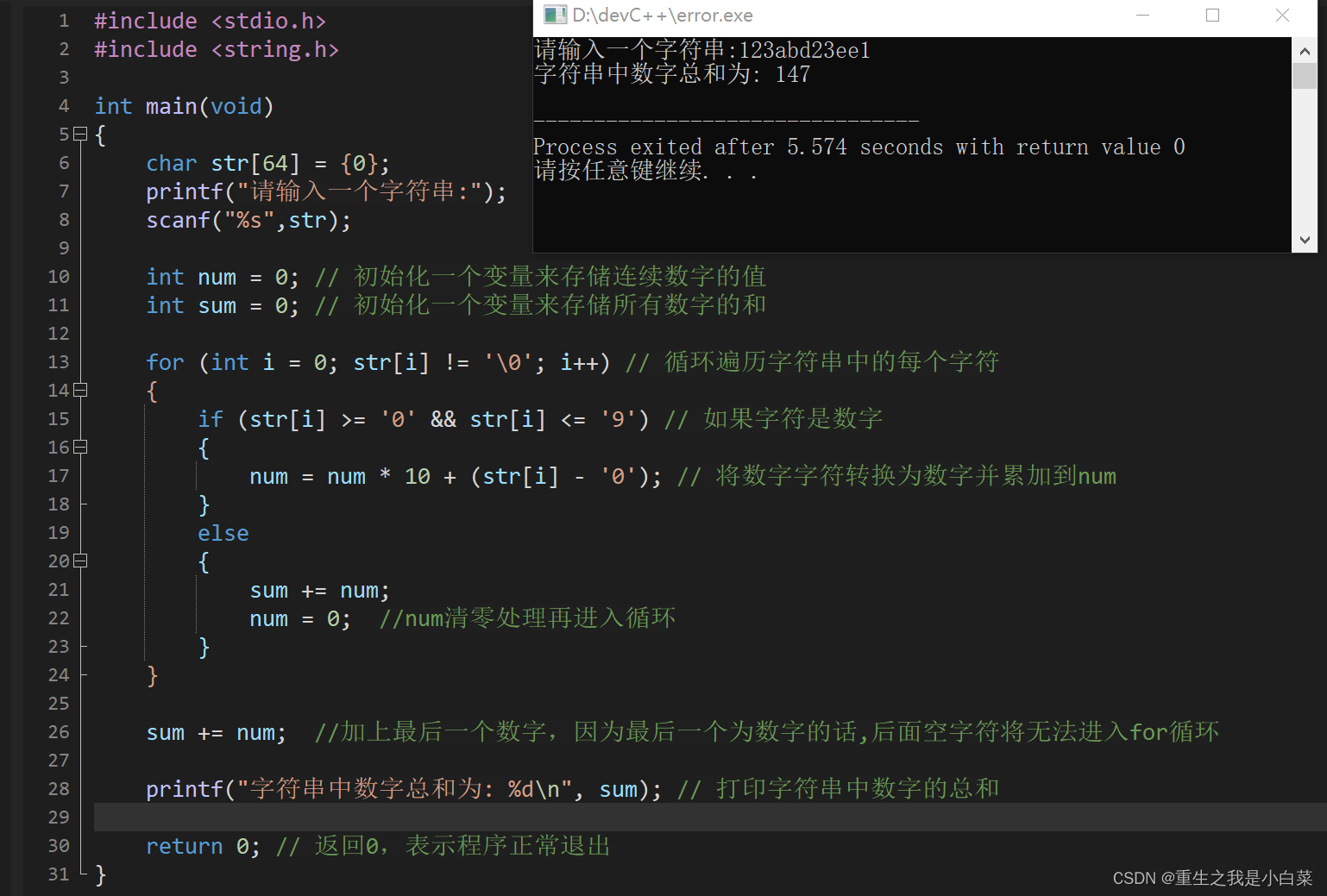
C语言—字符数组(3)
可能不是那么的完整,先凑合看吧,如果我学会如何修改以后,我慢慢回来修改的 1.编写程序实现对两个字符串的连接功能; 法一:不使用strcat函数,写程序直接实现,记得添加结束符,不然程序访问数组时候将变得不…...

linux 实用技能
1.查看系统版本 cat /etc/redhat-release cat /etc/redhat-release 2. 查看磁盘实用情况 df du 3.查看内存 top -Hp 2214 4. 网络配置 vi /etc/hostname vi /etc/hosts vi /etc/sysconfig/network-scripts/ifcfgens33 6. sed ‘s/a/b/g’ aaa.txt 替换 7. scp …...

【maya 入门笔记】基本视图和拓扑
1. 界面布局 先看基本窗口布局,基本窗口情况如下: 就基本窗口布局的情况来看,某种意义上跟blender更像一点(与3ds max相比)。 那么有朋友就说了,玛格基,那blender最下面的时间轴哪里去了&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
