CSDN 编程竞赛三十四期题解
竞赛总览
CSDN 编程竞赛三十四期:比赛详情 (csdn.net)
本期的题目和第三十一期竞赛的题目竟然高度重合,真不知道该写点什么了。
不过,上次那道测试数据有bug的题已经修复了,答题过程挺顺利的,没有遇到新的问题。
竞赛题解
题目1、最优利润值
你在读的经营课程上,老师布置了一道作业。在一家公司的日常运营中,会对一些商品的价格走势根据一些经验和数据进行预估,并据此进行决策。例如,假设某商品每天的价格都有可能变动,我们要做的就是低买高卖获得最高利润。比如,假设我们预估该商品接下来七天内的价格走势如下:4 1 2 3 6 4 8,那我们采取的最佳策略是在价格1块钱的时候买入,在价格8块钱的时候卖出。为了简化整个过程,我们限定在此周期内只能有一次买入一次卖出,且商品在没有购入前是无法卖出的,即该商品不是期货而是现货。现要求你用程序来实现自动决策。输入一定天数的商品预估价格,自动计算出最优利润值。例如,上面的例子中,最优利润值为8-1=7(简单起见,只考虑0到100000之间的整数价格)。
#include <cstdio>int data [100005];int main () {int result = 0;int n = 0;while (scanf ("%d", &data [n]) != EOF) n++;for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {int val = data [j] - data [i];if (result < val) result = val;}}return 0;
}题目2、爱吃鬼
小艺酱每天都在吃和睡中浑浑噩噩地度过。可是肚子是有空间上限v的。小艺酱有n包零食,每包零食占据肚子空间a [i],并会给小艺酱一个甜蜜值 b [i]。小艺酱想知道自己在肚子空间上限允许范围内最大能获得的甜蜜值是多少?
#include <cstdio>int a [1005];
int b [1005];
int dp [1005];int main () {int v, n;scanf ("%d %d", &v, &n);for (int i = 0; i < n; i++) scanf ("%d %d", &a [i], &b [i]);for (int i = 0; i < n; i++) {for (int j = a [i]; j <= v; j++) {dp [j] = max (dp [j], dp [j - a [i]] + b [i]);}}printf ("%d", dp [v]);return 0;
}题目3、开学趣闻之美食诱惑
小艺酱又开学了,可是在上学的路上总会又各种意想不到的美食诱惑让小艺酱迟到。假设小艺酱家到学校是一个n*n的矩阵。每个格子包含一个诱惑值p,诱惑着小艺,让她迟到。小艺位于矩阵的左上角,学校在矩阵的右下角。小艺想知道自己到达学校所要经历的最小诱惑值是多少?
int main () {int n;scanf ("%d", &n);int data [n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {scanf ("%d", &data [i][j]);}}int dp [n][n];dp [0][0] = data [0][0];for (int i = 1; i < n; i++) dp [0][i] = dp [0][i - 1] + data [0][i];for (int i = 1; i < n; i++) dp [i][0] = dp [i - 1][0] + data [i][0];for (int i = 1; i < n; i++) {for (int j = 1; j < n; j++) {dp [i][j] = min (dp [i - 1][j], dp [i][j - 1]) + data [i][j];}}return 0;
}刚开始角色位于(0, 0)位置,且必定吃到左上角起始位置处的诱惑值。
接下来角色可以向右或者向下走,先分别计算出来仅向右走和仅向下走能吃到的诱惑值。
边界计算完成之后,就可以进入地图内部进行计算了。例如,从(0,0)走到(1,1),有两种方法,先向右后向下,和先向下后向右,这时就可以利用之前算好的边界条件的值了。假设先向右后向下,那么先从(0,0)走到(0,1),再从(0,1)走到(1,1)。这个过程中,从(0,0)走到(0,1)已经计算过了,直接用计算好的结果加上(1,1)处的诱惑值即可。这也就是动态规划算法的核心思想了,将计算过的数据存起来,后面的计算可以用上前面计算出来的结果,减少重复计算的时间,提升效率。
动态规划算法从小规模问题扩展到大规模的问题,每一步存储的都是当前规模下的最优解。全部计算完成之后,输出右下角那个格子上的诱惑值即可,这就是从左上角到右下角的最小诱惑值。
有小伙伴私信问博主,为什么不能向左或者向上走?这个其实是题目描述的问题了,这道题的原型是机器人寻路问题,这是学动态规划时的一道标准例题,在网上通过教程自学动态规划的小伙伴,可能多少会对这道题有点印象。
机器人路径问题:https://blog.csdn.net/weixin_45975835/article/details/117331825
可以参考一下这位博主写得文章。
题目4、小艺照镜子
已知字符串str。输出字符串str中最长回文串的长度。
int match (std::string str) {int result = 1;for (int i = 0; i < str.length (); i++) {for (int j = 0; j < 2; j++) {int left = i - j;int right = i + 1;while (left > -1 && right < str.length () && str [left] == str [right]) {left--;right++;}int len = right - left - 1;if (result < len) result = len;}}return result;
}直接从左向右查找回文串,时间复杂度为O(N^3),会超时。
使用中心扩展法,从每个位置向两边查找,不是回文串就停下,这样可以将复杂度优化到O(N^2度。
查找时,回文串分为奇回文串(aba)和偶回文串(abba),这里需要分别计算两种情况下的回文串长度。如果当前位置无法向左向右扩展成回文串,那么它的长度是1(这个字符本身构成一个回文串,例如 a 自身可以构成一个长度为 1 的回文串)。
相关文章:

CSDN 编程竞赛三十四期题解
竞赛总览 CSDN 编程竞赛三十四期:比赛详情 (csdn.net) 本期的题目和第三十一期竞赛的题目竟然高度重合,真不知道该写点什么了。 不过,上次那道测试数据有bug的题已经修复了,答题过程挺顺利的,没有遇到新的问题。 竞…...

C#教程06 运算符
文章目录 一、算术运算符加法运算符(+)减法运算符(-)乘法运算符(*)除法运算符(/)二、逻辑运算符与运算符(&&)或运算符(||)非运算符(!)三、比较运算符等于运算符(==)大于运算符(>)小于运算符(<)大于等于运算符(>=)小于等于运算符(<=…...
pytest单元测试)
软测入门(六)pytest单元测试
pytest pytest是python的一种单元测试框架,同自带的unit test测试框架类似,但pytest更简洁高效。 单元测试: 测试 函数、类、方法能不能正常运行测试的结果是否符合我们的预期结果 安装 pip install -U pytest基本使用 通过pytest包使用…...
)
经典分类模型回顾5—DenseNet实现图像分类(matlab)
DenseNet,全称为Densely Connected Convolutional Networks,中文名为密集连接卷积网络,是由李沐等人在2017年提出的一种深度神经网络架构。 DenseNet旨在解决深度神经网络中的梯度消失问题和参数数量过多的问题,通过构建密集连接…...
基于flask+bootstrap+echarts+mysql的鱼村小馆订餐后台管理系统
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...

Spark使用Log4j将日志发送到Kafka
文章目录自定义KafkaAppender修改log4j.properties配置启动命令配置添加参数启动之后可以在Kafka中查询发送数据时区问题-自定义实现JSONLayout解决自定义JSONLayout.java一键应用可能遇到的异常ClassNotFoundException: xxx.KafkaLog4jAppenderUnexpected problem occured dur…...

c++类与对象整理(上)
目录 1.类的引入 2.类的定义 3.类的访问限定符及封装 1)访问限定符 2)封装 4.类的作用域 5.类的实例化 6.类的对象大小的计算 1)类对象的存储方式 2)内存对齐和大小计算 编辑 7.类成员函数的this指针 1)…...
什么是镜像的元数据?)
Docker学习(十九)什么是镜像的元数据?
在 Docker 中,镜像的元数据是指与镜像相关的所有信息,包括镜像的名称和标签、作者、描述、创建日期、环境变量、命令等。这些信息都是通过 Dockerfile 或命令行创建和指定的。 镜像的元数据被存储在 Docker Registry 中,并在使用 docker pull…...

Python如何获取弹幕?给你介绍两种方式
前言 弹幕可以给观众一种“实时互动”的错觉,虽然不同弹幕的发送时间有所区别,但是其只会在视频中特定的一个时间点出现,因此在相同时刻发送的弹幕基本上也具有相同的主题,在参与评论时就会有与其他观众同时评论的错觉。 在国内…...

JAVA- AOP 面向切面编程 Aspect切面工具类 记录特定方法执行时的入参、执行时间、返参等内容
背景:JAVA项目,使用AOP对指定函数进行切面。能够记录特定方法执行时的入参、执行时间、返参结果等内容。 文章目录1、自定义注解类1.1 Target1.2 Retention2、Aspect切面工具2.1 JointPoint2.2 Pointcut2.3 切面中的相关注解3、同一个类里调用AOP4、其他…...

「史上最全的 TCG 规范解读」TCG 规范架构概述(下)
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强不同计算机平台上计算环境的安全性。TCG 于 2003 年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Allia…...

GDScript 导出变量 (4.0)
概述 导出变量的功能在3.x版本中也是有的,但是4.0版本对其进行了语法上的改进。 导出变量在日常的游戏制作中提供节点的自定义参数化调节功能时非常有用,除此之外还用于自定义资源。 本文是(Bilibili巽星石)在4.0官方文档《GDScr…...

JAVA知识点全面总结6:泛型反射和注解
六.JAVA知识点全面总结6泛型反射和注解 1.什么是泛型?可以用在哪里? 2.泛型擦除机制是什么?为什么擦除? 3.通配符是什么?作用是什么? 未更新 1.注解是什么?有什么用? 2.注解的自定义和实…...
和激进的死代码删除(ADCE,Aggressive DCE))
死代码删除(DCE,Dead Code Elimination)和激进的死代码删除(ADCE,Aggressive DCE)
死代码删除(DCE,Dead Code Elimination)和激进的死代码删除(ADCE,Aggressive DCE)死代码删除(DCE,Dead Code Elimination)DCE简介DCE基本算法激进的死代码删除࿰…...

询问new bing关于android开发的15个问题(前景、未来、发展方向)
前言:new bing是基于chat-gpt的新搜索工具,可以采用对话方式进行问题搜索,经过排队等候终于可以使用new bing,询问了目前我最关心的关于android开发几个问题 文章目录1.如何学好android开发?2.android开发能做什么?3.…...
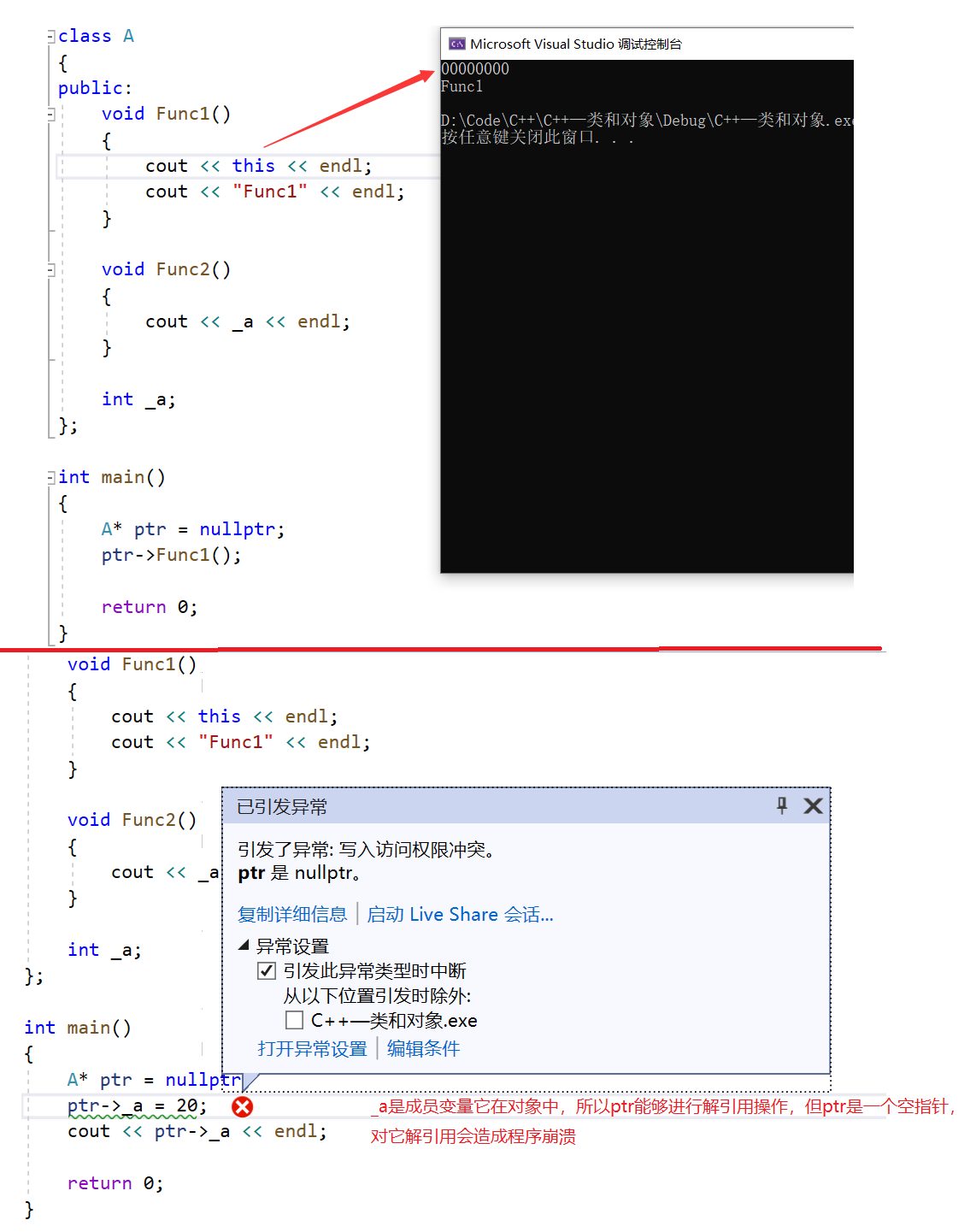
【C++】初识类和对象
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录前言一、面向过程和面向对象初步认识二…...
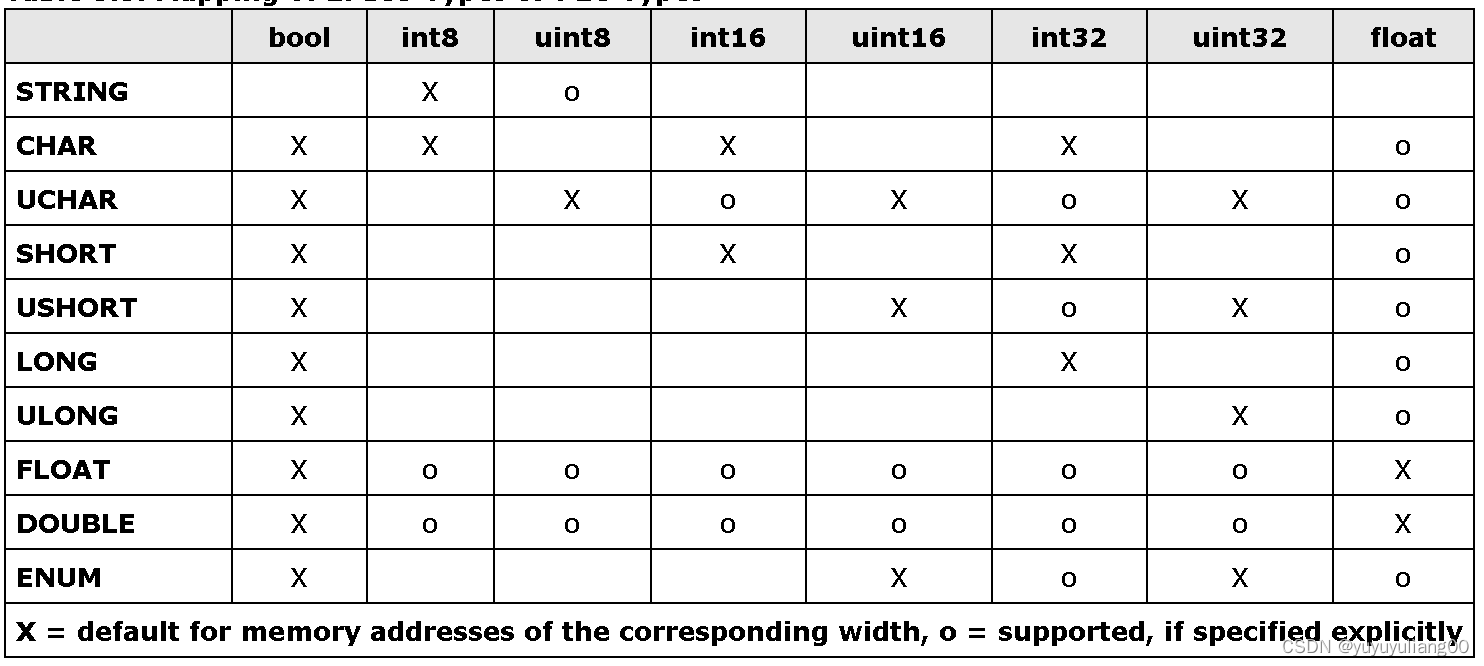
EPICS S7nodave手册
第一章:介绍 本手册分为6章(不算次介绍部分)。第一章介绍s7nodave用于EPICS的设备支持的概念和特新。第二章描述启动一个使用s7nodave的IOC项目所需要的几步。第三章描述s7nodave支持的IOC shell命令。之后,第四章解释s7nodave支持的各种记录类型。最后…...
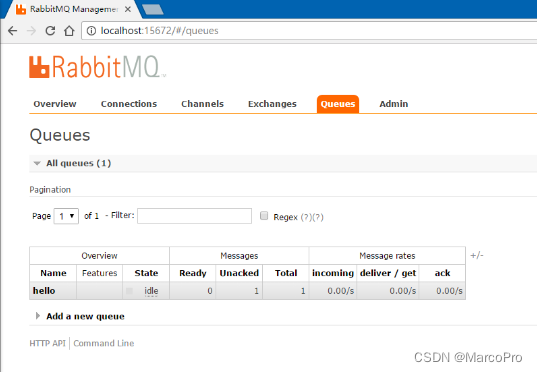
2023最新版本RabbitMQ的持久化和简单使用
上节讲了 RabbitMQ下载安装教程 , 本节主要介绍RabbitMQ的持久化和简单使用。 一、RabbitMQ消息持久化 当处理一个比较耗时得任务的时候,也许想知道消费者(consumers)是否运行到一半就挂掉。在当前的代码中,当RabbitM…...

函数式编程
函数式编程(一) 文章目录函数式编程(一)1. 前言1.1 概念2. Lambda 表达式2.1 概述2.2 基本的格式2.3 触发条件2.4 Lambda表达式2.4.1 无参无返回值2.4.2 有参无返回值2.4.3 无参数有返回值2.4.4 有参有返回值【重点】2.4.4.1 比较…...
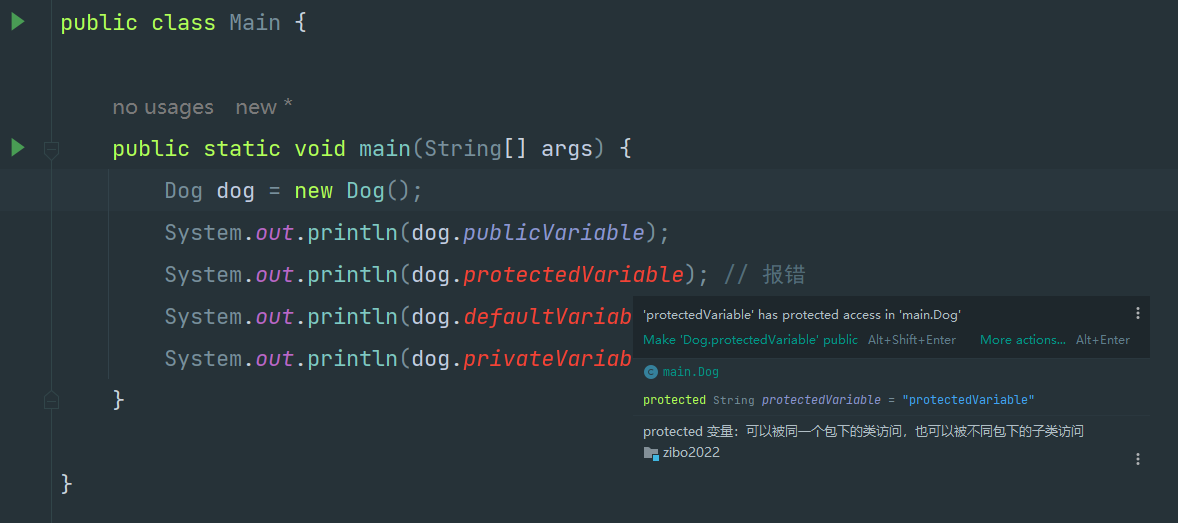
【Java 类】001-访问修饰符、命名规范
【Java 类】001-访问修饰符、命名规范 文章目录【Java 类】001-访问修饰符、命名规范一、访问修饰符概述1、是什么2、作用作用问题3、访问修饰符有哪些4、作用对象二、访问修饰符使用演示1、类访问修饰符演示第一步:创建 Dog 类:public第二步:…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
