排序算法整理
- 排序种类
- 排序特性
- 代码背景
- 基于插入的排序
- 直接插入排序
- 原理
- 代码
- 折半查找排序
- 2路查找排序
- 希尔排序(shell) 缩小增量排序
- 原理
- 代码
- 基于交换的排序
- 冒泡排序
- 原理
- 代码
- 快速排序(重要!)
- 原理
- 我的思考
- 代码
- 基于选择的排序
- (简单)选择排序
- 原理
- 代码
- 堆排序
- 原理
- 思考
- 代码
- 其他排序
- 归并排序(2路归并
- 原理
- 思考
- 代码
- 基于统计的排序
- 总结
本文是我学习排序算法的笔记,包含了知识点归纳、我对算法的思考、我的代码
如有误欢迎指出
本文使用语言:C++
排序种类
基于插入:直接插入排序算法、希尔排序算法
基于交换:冒泡排序算法、快速排序算法
基于选择:简单选择排序算法、堆排序算法
其他:归并排序、基于计数的排序
(基于计数的排序无代码
排序特性
- 是否就地排序
- 是内部排序还是外部排序(外部排序就是用到外存了,如果排序的数据能一次放到内存中,直接在内存排序,不涉及与外存交互,就是内部排序)
- 稳定排序还是不稳定排序(稳定排序就是,“==”的数据,相对位置不用变化
- 时间复杂度
文末有特性总结
代码背景
所有代码都用下方全局数组和main函数作测试
/*测试样例
20
23523 51345 1345314 9876 8765 2345 4 3 8 7
5 4 2349 1 54 29 53 98 275946382 305
*/
#include <iostream>
using namespace std;
int nums[105];
int n;
int main()
{//数组初始化cin >> n;for (int i = 1; i <= n; i++){cin >> nums[i];}//任何一个排序算法的函数调用一次//排序后展示for (int i = 1; i <= n; i++){cout << nums[i] << ' ';}cout << endl;
}
基于插入的排序
直接插入排序
特性:就地、稳定(看插入位置如何选择)、O( n 2 n^2 n2)
原理
以数组第一个元素为有序区,后面都算无序,每一次有序区长度增加1,将加入的元素顺序插入有序区中,完成排序
代码
void straightInsertSort()
{int new_insert; //新插入数的值int insert_index; //新插入数的应该插入的位置for (int i = 2; i <= n; i++) //i表示有序区长度{new_insert = nums[i]; //插入有序区的元素值insert_index = i; //避免完全不需要插入,导致insert_index = 0 !!!!!!!!!!for (int j = 1; j < i; j++){if(new_insert < nums[j]) //找到需要插入的位置{insert_index = j;break;}}for (int j = i; j > insert_index; j--)//从插入位置到有序区末尾,整体向右滑动{nums[j] = nums[j-1];}nums[insert_index] = new_insert;}
}
折半查找排序
查找需要插入位置时使用二分查找的方式,优化效果很一bamn,因为查找到之后的插入操作仍然是O(n)
特性:就地、稳定(看插入位置如何选择)、O( n 2 n^2 n2)
2路查找排序
优化插入操作的时间复杂度,用循环数组减少一半插入时间,这样会让排序变成非就地的,然而还是O(N),效果依旧一bamn
特性:就地、稳定(看插入位置如何选择)、O( n 2 n^2 n2)
希尔排序(shell) 缩小增量排序
会发现,数据量少且基本有序时,插入排序效率很高
特性:就地、不稳定(因为进行了跳跃的插入排序),时间复杂度(最坏时间复杂度O( n 2 n^2 n2))
原理
那么,将数组切分成多个小段,依次插入排序(这个时候每一段的数据量就很少),然后依次将每一段拼起来(拼起来的时候就是基本有序的情况)
Q:如何分段(分组)?
A:分d组,就以d为增量,先分n/2组,排序,减少到n/4组,直到1组(取n/2就是希尔增量)

会发现,希尔排序的作用就体现在数据量多时,要将小的值插入左边,可以很快地跳着插入,因为每一组很小,但其实在原数组上又很远!如果是直接插入排序的话要挪一整条数据,但是分组后只用挪一点点数据
Q:那我怎么对每一个跳着连接的组排序,比较方便?
A:以d为排序时插入的增量,每插入完一次可以直接++,给另一个组进行插入,就可以一个for循环,给每个组都排序了!
这时也会发现,其实分组、排序过程中的组数都没必要算了,只需要遍历增量就行
代码
void shellSort()
{int d = n/2;int new_ins; //新插入的值while(d>0){for (int i = 1+d; i <= n; i++){new_ins = nums[i];int j;for ( j = i-d ; j > 0 ; j-= d)//从右往左找插入的位置,刚好适合 基本有序 的情况下进行直接插入排序{if(nums[j] > new_ins)nums[j+d] = nums[j];//后移elsebreak;}nums[j+d] = new_ins; //插入}d/=2;//缩小增量}
}
基于交换的排序
冒泡排序
特性:就地、稳定、O( n 2 n^2 n2)
原理
每一次依次比较相邻元素,把最大的值往最后交换
代码
优化本次循环完全排序好的情况
#include <iostream>
using namespace std;
int nums[105];
int n;void bubbleSort()
{bool sorted = true;int tmp;for (int i = 1; i <= n; i++){sorted = true; //优化已经完全排好序的情况,那已经局部排序好的情况呢?for (int j = 1; j <= n - i; j++){if (nums[j] > nums[j + 1])//交换{tmp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tmp;sorted = false;}}if (sorted)break;}
}
优化局(尾)部已经排序好的情况,确定出已经有序部分和⽆序部分的边界
void bubbleSort()
{int unSortedCnt = n; //未排序的头部的长度,乱序区长度int tmpUnSortedCnt = n;int tmp;while (unSortedCnt > 1) //未排序长度为1时即完全排好序了{for (int j = 1; j < unSortedCnt; j++){if (nums[j] > nums[j + 1]) //交换{tmp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tmp;tmpUnSortedCnt = j; //更新,最后一次更新时就表示当前j到n都是有序的}}if (tmpUnSortedCnt == unSortedCnt)//没有更新,说明已经完全排好序break;unSortedCnt = tmpUnSortedCnt;}
}
快速排序(重要!)
特性:就地,不稳定,O(nlogn)
这里时间复杂度我的理解
- 每一层递归的时间复杂度O(n)
如果某时刻遍历到第 x x x 层,此时数组被拆成 2 x 2^x 2x 份,无论 2 x 2^x 2x 多大,这一层需要进行的比较(即类似下面代码中arr[i] > x的判断)都是n遍
即要走完数组内每一个元素(其实不完全准确,第 x x x 层的基准值到第 ( x + 1 ) (x+1) (x+1)层的时候就不需要进行比较了)
- 递归的趟数对应时间复杂度O(logn),原因参考下面我的思考
关于不稳定性:
数组中出现3个相等值,可能发生位置变化
原理
选一个基准 x x x 作“中点”,把小于 x x x 的放 x x x 左边,大于 x x x 的放右边,依次继续在左右进行这个操作(这个操作完成后基准 x x x 的位置就已经确定了,这个基准 x x x 就是“已排序”状态了)直到完成排序
实现:
以左边为基准,在尾部往头找比基准小的数,在头部往尾部找比基准大的数,依次交换
这个排序包含了递归的思想,所以这会是个递归函数
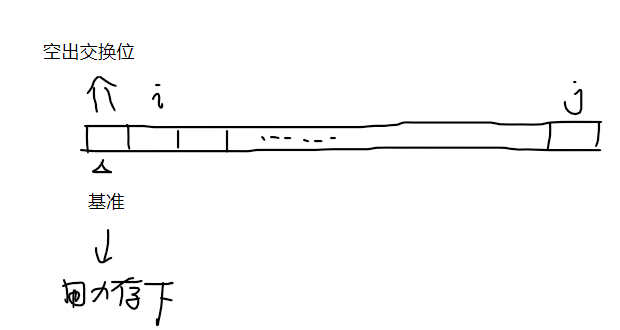
举例:
下面是定位一次基准值的步骤
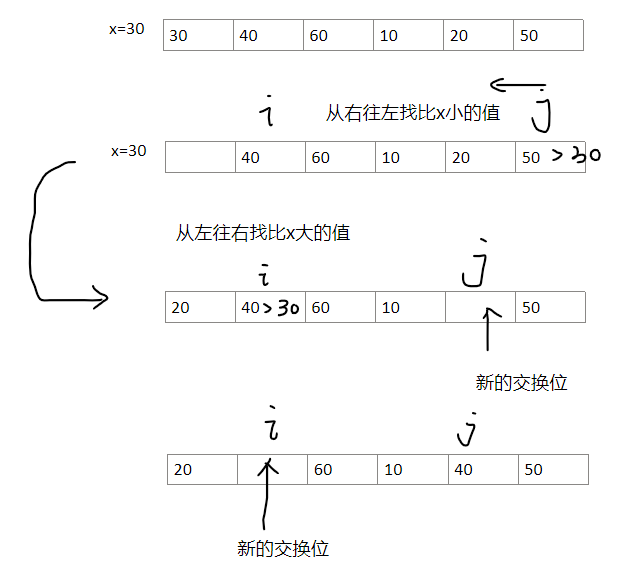
最终得到:
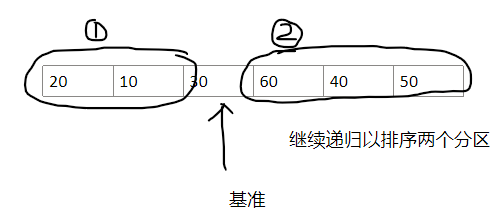
我的思考
快速排序思想里最核心的就是这个基准分界带来的倍增作用,因为每一次把一个基准值定位成功,都会让下一次时间复杂度为 O ( n ) O(n) O(n) 的一趟遍历定位基准值的数量翻倍(注意,但是如果这个基准值是当前区间的最值的话就不会翻倍
如上面的例子,第一遍遍历确认了 30 30 30 的位置,那么下一次遍历就会确认出 20 20 20 和 60 60 60 两个数!所以,遍历整个数组的趟数是 O ( l o g n ) O(logn) O(logn) 的,这是清清楚楚,一目了然的!
可以看出,快速排序的优秀之处,就是作为一个基于交换的排序(交换的时候会有位置互换,这个过程就能产生“信息”,比如基准值左边的值一定就在基准值左边,那么左边遍历完会有一个定位结果,右边就也一定会),在耗时为 O ( n ) O(n) O(n) 的定位操作的过程中(就是选择的过程),让下一次同样的一次遍历,通过交换定位出的基准位置得到的信息,得到更多的定位结果,以此提高效率
代码
/* 调用方式 quickSort(nums,1,n);
*/
void quickSort(int arr[],int l,int r)
{if(l<r){int i = l;int j = r;int x = arr[l];//为了避免每次交换需要用个tmp,我选择每次和x比较,最后再将x赋值到定位好的点while(i<j){while( i<j && arr[j] > x)j--;//从右往左找比x小的值if(i<j) arr[i++]=arr[j];//需要判断一下,避免已经j==i了,然后i++导致j<iwhile( i<j && arr[i] < x)i++;//从左往右找比x大的值if(i<j) arr[j--]=arr[i];}//最后还需要覆盖中间的基准值arr[i]=x;quickSort(arr,l,i-1);quickSort(arr,i+1,r);}
}
基于选择的排序
(简单)选择排序
特性:就地,不稳定,O( n 2 n^2 n2)
不稳定性来源于交换时,是跳跃的,比如{3,3,1},第一个3会跑到结尾
原理
每一次在待排序区中找最小的,放到最左边,依次直到待排序区长度为0
代码
void selectionSort()
{int min_p,tmp;for (int i = 1; i < n; i++){min_p=i;for (int j = i+1; j <= n; j++){if(nums[j]<nums[min_p]) min_p=j;}tmp = nums[i];nums[i] = nums[min_p];nums[min_p] = tmp;}
}
堆排序
特性:就地,不稳定,O(nlogn)
不稳定性:显然堆的调整的跳跃性会让重复数据相对位置发生改变
原理
堆可以实现用 O ( l o g n ) O(logn) O(logn) 的时间复杂度调整出最小值,来优化简单选择排序的效率
参考 大顶堆、小顶堆 这一篇,可知,用调整堆内子树的方式,依次找最小值,在第一次找到最小值用 O ( n l o g n ) O(nlogn) O(nlogn) 之后(也就是堆初始化),每一次找最小值只需要完成一次堆调整的操作 O ( l o g n ) O(logn) O(logn),执行剩下的 n − 1 n-1 n−1 次
原理:
先初始化出小顶堆,然后将顶列入已排序区,将堆数组尾部的数组提到顶部,进行 O ( l o g n ) O(logn) O(logn)的堆调整操作,以此往复,直到每个顶都依次进入排序区
实现:
我的思路是为了排序的就地性,这样操作,作大顶堆,把顶和数组尾部交换(也就是已排序区是从数组尾部往头部生长的),这个操作即完成了排序区的 fill in,还完成了堆的更新,下一步就可以直接开始堆调整操作了
图示:最终就是从右往左依次变小,就是升序了
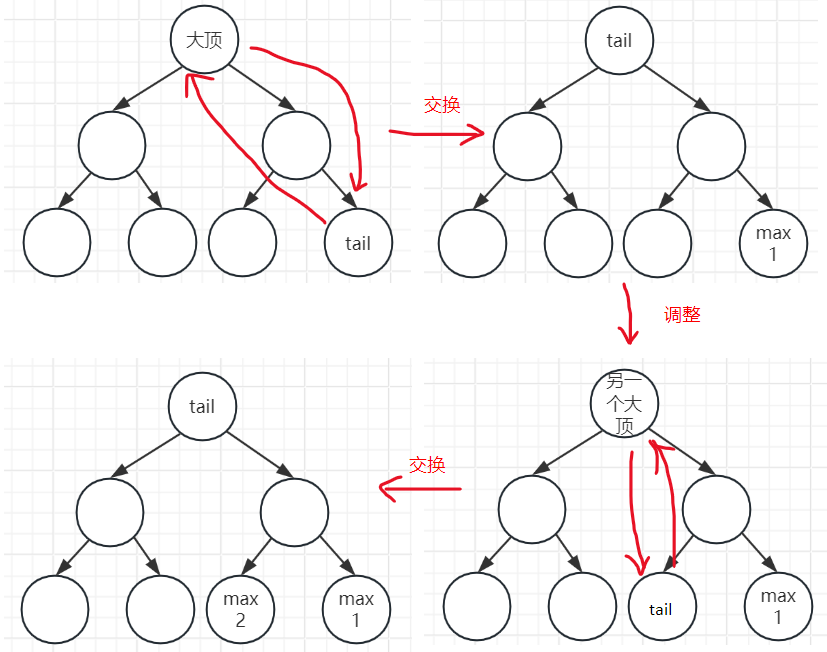
思考
这个思路的逻辑感觉和快速排序也是有相通之处的,快速排序让每次遍历排序的结果倍增,而堆排序让每次选择的效率翻倍
因为选择排序要做工作是,找到最值,压如排序区,往复
而找到最值的过程,也是有“信息”的,电脑记不住,但我们可以用一个逻辑帮他组织出来,堆排序用的就是堆的逻辑,
对一个大顶堆
我们 拿去根结点 = 找到最值,然后压入排序区,然后,我们替换根结点后,维护大顶堆,修复这个大顶堆 = 再次找到最值,而因为大顶堆的树状结构,我们找的新最大值已经在大顶堆根节点的左右手边上恭候多时了,只是为了保证下一次大顶堆每一个子树也是这个准备就绪的状态,需要 O ( l o g n ) O(logn) O(logn) 的维护时间,因为是树,每一次分支可以减少一半的判断,堆的维护也就比较高效
那为什么C++ sort()函数优先用快速排序而不是堆排序呢?
我没有做过调查研究,但是可以猜测一下,或许是在快速排序没有很坏的情况下,操作步数大致是 n l o g n nlog{n} nlogn,而堆排序因为数组自我初始化的过程就需要消耗大致 n 2 l o g n \frac{n}{2}logn 2nlogn 的步数了,完了排序还要操作 n l o g n nlogn nlogn 遍,可能会久一点,很无脑的猜测……
代码
/// @brief 维护大顶堆的函数(对子树A,A的子树都为大顶堆时,维护A子树的大顶堆状态
/// @param heap 堆数组
/// @param i 子树A根节点索引
/// @param n 子树A的最大索引值(尾部叶子
void adjustDown(int heap[],int i,int n)
{int child_p = 2 * i; //i结点(在循环中是指对应调整的子树)的孩子的索引int parent = heap[i]; //本子树的根结点的值while (child_p<=n) //保证双亲是有孩子结点的,叶子结点本身就是排好的堆,不需要调整{if (child_p + 1 <= n && heap[child_p + 1] > heap[child_p]) child_p++;//选中左右孩子中更小的和双亲作比较if (heap[child_p] > parent){heap[child_p / 2] = heap[child_p];//将孩子的值赋给父亲child_p *= 2;}else{break;}}heap[child_p/2] = parent;//这一步容易忘记!!!!就是赋回i结点的值!当然如果每次比较完用tmp去做交换就可以不用这么麻烦,我就是不想用tmp交换,因为那样有三次赋值,而这样写只有一次
}//堆排序代码
void heapSort()
{//初始化大顶堆for (int i = n/2; i > 0; i--){adjustDown(nums,i,n);}int tmp;for (int i = 1; i < n; i++)//在i=n-1并开始循环时,已排序区的长度为n-2,循环结束时已排序区长n-1,那头部也算是排好了,无需i=n再循环一遍{//头部和尾部交换(大顶堆的顶压如尾部已排序区tmp = nums[1];nums[1]=nums[n-i+1];nums[n-i+1]=tmp;//维护头部未排序区的大顶堆,此时只有根节点的树需要维护,其他的已经在初始化时维护好了adjustDown(nums,1,n-i);}
}
其他排序
归并排序(2路归并
特性:非就地,稳定,O(nlogn)
稳定性上,因为没有跳跃的比较交换,不会越过重复数据
原理
原理:
我倾向不以先拆再合并的方式去理解,他就是先以每一个单独的值作为已排好的数组,然后两两相邻的合并排序,最后合并成一个,显然就是合并 O ( n l o g n ) O(nlogn) O(nlogn) 趟
实现:
代码肯定还是从总数n出发,所以拆分2份,递归下去,直到长度为1,然后返回,得到的2份合并即可(本句搭配代码注释食用最佳
思考
先不说这个算法怎么做的,问一个问题,给你两个有序数组,把他俩放一起排序要多久, O ( n + m ) O(n+m) O(n+m) ,两个指针怼着两个数组的头然后遍历就行了,这就是归并排序的招式
所以就是线性复杂度的两两合并让已排序数组的长度翻倍,达到的高效,所以我认为功劳最大的是两已排序数组合并的线性时间复杂度,而不是这个二分合并(我也不知道咋叫,但学过二分查找的应该看得懂吧>_<)的思路,是这个线性时间复杂度给了归并排序用二分思想的底气
但是,但是,这个有序数组合并的过程,是需要开辟新的数组空间的,原因如下:
假设两数组为A、B(假设在原数组 n u m s nums nums中,A在左,B在右,AB相邻)
A [ i ] > B [ j ] A[i]>B[j] A[i]>B[j],并不能简单地将两者交换,因为 B [ j ] B[j] B[j]到 A A A里面是有序的,但是 A [ i ] A[i] A[i]到B里面就不一定了,为了提高时间效率,保证线性时间复杂度,需要开辟新的内存空间
代码
/* 调用方式mergeSort(nums,1,n);
*/
void mergeSort(int nums[],int l,int r)
{if(l>=r) return; //直到长度为1,然后返回int mid = l+(r-l)/2; //拆分2份mergeSort(nums,l,mid); //递归下去mergeSort(nums,mid+1,r); //得到的2份,合并即可int p1 = l;int p2 = mid+1;int tmpNums[105]; //临时数组与原数组等长int i = 1;while(p1<=mid && p2<=r){if(nums[p1]>nums[p2])tmpNums[i++]=nums[p2++];elsetmpNums[i++]=nums[p1++];}while(p1<=mid) tmpNums[i++]=nums[p1++];while(p2<=r) tmpNums[i++]=nums[p2++];i = 1;for (int j = l; j <= r; j++)//记得把临时表赋值回原表{nums[j] = tmpNums[i++];}
}
基于统计的排序
1. 计数排序
非就地,不稳定(可以优化为稳定的),时间复杂度O(n+b)(b是count数组的长度)但空间复杂度可能会很大,因为用于计数的数组长度可能过大,还可能导致时间复杂度大
原理:
- 记录最小、最大值,再记录从最小到最大值的所有数据的出现次数,存在count数组中
- count数组依次从小到大输出对应次数的值,完成排序
优化为稳定排序:
- 用一个index数组,作count的前缀和数组,意义是 i i i 这个值对应于排序好之后的最大索引
- 从原数组尾部遍历到头,遇到一个值,检索对应index数组的 “最大索引” ,这就是他应该呆的实际位置,然后对应index数组的 “最大索引” − 1 - 1 −1 即可
2. 桶排序
非就地,稳定性、时间复杂度取决于桶内排序效率
原理:
- 用数组内的值的范围分类,如每100一类,或每10一类(这样就可以通过 n u m s [ i ] / 10 nums[i]/10 nums[i]/10来分类),装在一个容器里
- 容器内再用之前的那些各种排序
- 最后合并
3. 基数排序
非就地,稳定,时间复杂度 O ( d × ( n + b ) ) O(d\times(n+b)) O(d×(n+b))(d是最大位数,b是count数组长度,10进制b=10
原理:(以十进制为例)
- 求出原数组的最高位(最低位
- 将所有数据补齐,填充0到最高位
- 从最低位开始,直到最高位,每一次对整个数组根据当前位数字进行稳定版本的计数排序即可
- 这样相当于用不同位进行有优先级的排序,优先级:高位的数字 > > > 低位的数字 > > > 原来处于数组的顺序
总结
| 算法 | 就地性 | 稳定性 | 时间复杂度 |
|---|---|---|---|
| 直接插入 | O | O | O( n 2 n^2 n2) |
| 希尔排序 | O | X | 最坏O( n 2 n^2 n2) |
| 冒泡排序 | O | O | O( n 2 n^2 n2) |
| 快速排序 | O | X | O( n l o g n nlogn nlogn) |
| 简单选择排序 | O | X | O( n 2 n^2 n2) |
| 堆排序 | O | X | O( n l o g n nlogn nlogn) |
| 归并排序 | X | O | O( n l o g n nlogn nlogn) |
| 计数排序 | X | X | O(n+b) |
| 桶排序 | X | 取决于桶内排序 | 取决于桶内排序 |
| 基数排序 | X | O | O ( d × ( n + b ) ) O(d\times(n+b)) O(d×(n+b)) |
相关文章:

排序算法整理
排序种类排序特性代码背景 基于插入的排序直接插入排序原理代码 折半查找排序2路查找排序希尔排序(shell) 缩小增量排序原理代码 基于交换的排序冒泡排序原理代码 快速排序(重要!)原理我的思考 代码 基于选择的排序(简单)选择排序…...

ONLYOFFICE 桌面应用程序 v8.0 发布:全新 RTL 界面、本地主题、Moodle 集成等你期待的功能来了!
目录 📘 前言 📟 一、什么是 ONLYOFFICE 桌面编辑器? 📟 二、ONLYOFFICE 8.0版本新增了那些特别的实用模块? 2.1. 可填写的 PDF 表单 2.2. 双向文本 2.3. 电子表格中的新增功能 单变量求解:…...
c语言---数组(超级详细)
数组 一.数组的概念二. 一维数组的创建和初始化2.1数组的创建2.2数组的初始化错误的初始化 2.3 数组的类型 三. 一维数组的使用3.1数组的下标3.2数组元素的打印3.2数组元素的输入 四. 一维数组在内存中的存储五. 二维数组的创建5.1二维数组的概念5.2如何创建二维数组 六.二维数…...

神经网络权重初始化
诸神缄默不语-个人CSDN博文目录 (如果只想看代码,请直接跳到“方法”一节,开头我介绍我的常用方法,后面介绍具体的各种方案) 神经网络通过多层神经元相互连接构成,而这些连接的强度就是通过权重ÿ…...

代码随想录训练营第三十九天|62.不同路径63. 不同路径 II
62.不同路径 1确定dp数组(dp table)以及下标的含义 从(0,0)出发到(i,j)有 dp[i][j]种路径 2确定递推公式 dp[i][j]dp[i-1][j]dp[i][j-1] 3dp数组如何初始化 for(int i0;i<m…...
学习大数据所需的java基础(5)
文章目录 集合框架Collection接口迭代器迭代器基本使用迭代器底层原理并发修改异常 数据结构栈队列数组链表 List接口底层源码分析 LinkList集合LinkedList底层成员解释说明LinkedList中get方法的源码分析LinkedList中add方法的源码分析 增强for增强for的介绍以及基本使用发2.使…...
Python 光速入门课程
首先说一下,为啥小编在即PHP和Golang之后,为啥又要整Python,那是因为小编最近又拿起了 " 阿里天池 " 的东西,所以小编又不得不捡起来大概五年前学习的Python,本篇文章主要讲的是最基础版本,所以比…...

解决vite打包出现 “default“ is not exported by “node_modules/...问题
项目场景: vue3tsvite项目打包 问题描述 // codemirror 编辑器的相关资源 import Codemirror from codemirror;error during build: RollupError: "default" is not exported by "node_modules/vue/dist/vue.runtime.esm-bundler.js", impor…...

c语言strtok的使用
strtok函数的作用为以指定字符分割字符串,含有两个参数,第一个函数为待分割的字符串或者空指针NULL,第二个参数为分割字符集。 对一个字符串首次使用strtok时第一个参数应该是待分割字符串,strtok以指定字符完成第一次分割后&…...
hash,以及数据结构——map容器
1.hash是什么? 定义:hash,一般翻译做散列、杂凑,或音译为哈希,是把任意长度的输入(又叫做预映射pre-image)通过散列算法变换成固定长度的输出, 该输出就是散列值。这种转换是一种压缩映射&…...

AIoT网关 人工智能物联网网关
AIoT(人工智能物联网)作为新一代技术的代表,正以前所未有的速度改变着我们的生活方式。在这个智能时代,AIoT网关的重要性日益凸显。它不仅是连接智能设备和应用的关键,同时也是实现智能化家居、智慧城市和工业自动化的必备技术。 一…...

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的鸟类识别系统(Python+PySide6界面+训练代码)
摘要:本文详细阐述了一个利用深度学习进行鸟类识别的系统,该系统集成了最新的YOLOv8算法,并与YOLOv7、YOLOv6、YOLOv5等先前版本进行了性能比较。该系统能够在图像、视频、实时视频流和批量文件中精确地识别和分类鸟类。文中不仅深入讲解了YO…...

核密度分析
一.算法介绍 核密度估计(Kernel Density Estimation)是一种用于估计数据分布的非参数统计方法。它可以用于多种目的和应用,包括: 数据可视化:核密度估计可以用来绘制平滑的密度曲线或热力图,从而直观地表…...

先进语言模型带来的变革与潜力
用户可以通过询问或交互方式与GPT-4这样的先进语言模型互动,开启通往知识宝库的大门,即时访问人类历史积累的知识、经验与智慧。像GPT-4这样的先进语言模型,能够将人类历史上积累的海量知识和经验整合并加以利用。通过深度学习和大规模数据训…...
重铸安卓荣光——上传图片组件
痛点: 公司打算做安卓软件,最近在研究安卓,打算先绘制样式 研究发现安卓并不像前端有那么多组件库,甚至有些基础的组件都需要自己实现,记录一下自己实现的组件 成品展示 一个上传图片的组件 可以选择拍照或者从相册中…...
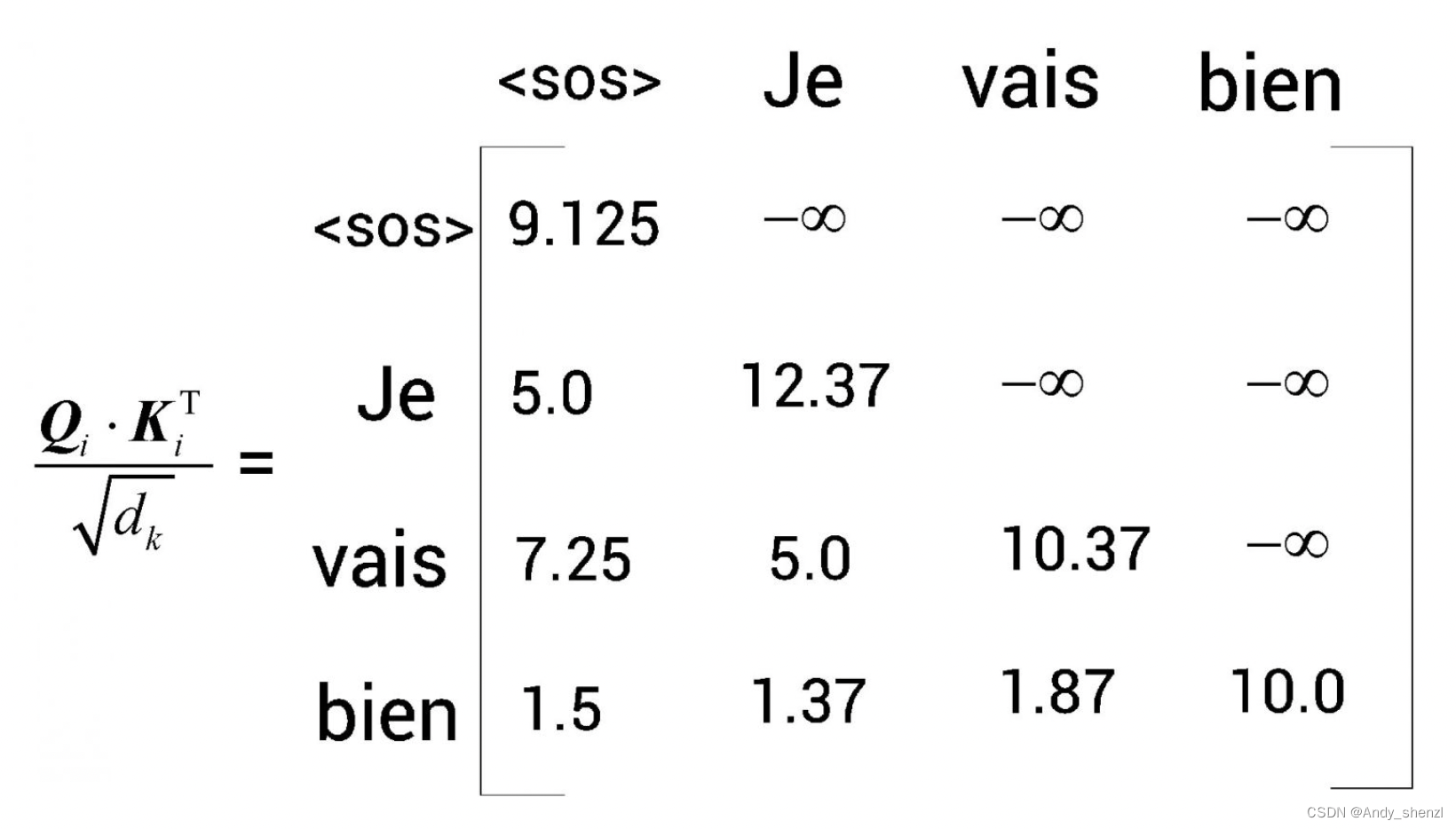
Bert基础(四)--解码器(上)
1 理解解码器 假设我们想把英语句子I am good(原句)翻译成法语句子Je vais bien(目标句)。首先,将原句I am good送入编码器,使编码器学习原句,并计算特征值。在前文中,我们学习了编…...

Visual Studio快捷键记录
日常使用Visual Studio进行开发,记录一下常用的快捷键: 复制:CtrlC剪切:CtrlX粘贴:CtrlV删除:CtrlL撤销:CtrlZ反撤销:CtrlY查找:CtrlF/CtrlI替换:CtrlH框式选…...

分享84个Html个人模板,总有一款适合您
分享84个Html个人模板,总有一款适合您 84个Html个人模板下载链接:https://pan.baidu.com/s/1GXUZlKPzmHvxtO0sm3gHLg?pwd8888 提取码:8888 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集…...

vue使用.sync和update实现父组件与子组件数据绑定的案例
在 Vue 中,.sync 是一个用于实现双向数据绑定的特殊修饰符。它允许父组件通过一种简洁的方式向子组件传递一个 prop,并在子组件中修改这个 prop 的值,然后将修改后的值反馈回父组件,实现双向数据绑定。 使用 .sync 修饰符的基本语…...

C语言系列15——C语言的安全性与防御性编程
目录 写在开头1 缓冲区溢出:如何防范与处理1.1 缓冲区溢出的原因1.2 预防与处理策略 2. 安全的字符串处理函数与使用技巧2.1 strncpy函数2.2 snprintf函数2.3 strlcpy函数2.4 使用技巧 3 防御性编程的基本原则与实际方法3.1 基本原则3.2 实际方法 写在最后 写在开头…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
