nginx服务

“欢唱吧,呼唤它,回来啊~”
Web服务器简介
Web服务器,一般是指“网站服务器”,其本质就是驻留于互联网中,某一台机器(计算机)上的进程(程序)。Web服务器通常就是为用户提供信息浏览服务,更可以放置数据文件,让全世界下载。
Web 服务器,也称为“WWW 服务器”,主要功能是“提供网上信息浏览服务”。是 Internet(互联网)上发展起来的服务,也是发展最快和目前使用最广泛的服务。

Nginx简介
Nginx 是一款自由的、开源的、高性能的HTTP服务器和反向代理服务器,同时也供IMAP、POP3、SMTP 代理服务。其特点是占有内存少,并发能力强,事实上nginx的并发能力在同类型的网页服务器中表现较好。所以,Nginx本质就是一款Web服务器。
Nginx 作为 Web 服务器可以向各种浏览器等客户端提供浏览服务,所以我们可以使用手机、PC、平板通过浏览器,访问部署了Nginx服务的机器。
正向代理 vs 反向代理
我们可以想象如下场景:
我知道,远郊一处工厂,盛产快乐牌火腿肠。那是我小时候心念的美味食物。然而,身在市中的我,如果想要抵达远郊,再进入工厂与厂长沟通,购买火腿是很麻烦的……大概emm,会花费我 六七十的来回车费,这我可负担不起!于是乎,我只好将愿望寄托给楼下开店铺的商贩大妈,告诉她,如果她去那个工厂购进火腿,我会购买很多。大妈有自己的 老头乐,所以,对她而言进货火腿似乎不是那么麻烦,并且转卖的利润也是客观、持久的,所以,她二话没说就答应了下来。一旦,我想要吃火腿了,大妈就会乐呵着开着她的 老头乐 “替我” 购买。
这个过程,便是 正向代理!我将 需求 转交给了大妈,由大妈来替我发起请求,大妈为我服务
 同样,一家开在远郊的工厂,正因没什么名气,业绩惨淡,工厂运营艰难。突然有一天,厂长家里的二姑婆想起来了做食物供给的侄子,正好她们家开的商场正缺这份货物。于是乎,同厂长协商,让厂长将这个工厂的货物卖给自己。这样,厂子的销路便得到了解决。至于,厂长的二姑婆将食物卖给谁?这就不是他关心的了。
同样,一家开在远郊的工厂,正因没什么名气,业绩惨淡,工厂运营艰难。突然有一天,厂长家里的二姑婆想起来了做食物供给的侄子,正好她们家开的商场正缺这份货物。于是乎,同厂长协商,让厂长将这个工厂的货物卖给自己。这样,厂子的销路便得到了解决。至于,厂长的二姑婆将食物卖给谁?这就不是他关心的了。
这个过程,也就是 反向代理。我将需求转给二姑婆,但二姑婆的真正服务对象是她的顾客

区分正、反向代理服务器最主要的特征是,正向代理离客户端更近,是为客户端服务的(例如:加速器、校园网)。反向代理位于服务端,为服务器提供负载均衡、安全防护等功能(例如:Ngnix)。
搭建一个Ngnix网站
配置nginx源:
在Centos中,配置nginx的yum源:
rpm -Uvh \ http://nginx.org/packages/centos/8/x86_64/RPMS/nginx-1.24.0-1.el8.ngx.x86_64.rpmOPTIONS:
-U 升级软件包
-v 表示显示详细信息
-h 表示显示安装进度安装完成后,我们更新一下yum缓存:

使用yum源安装Nginx:
# 安装nginx
sudo yum install -y nginx# 检查版本
nginx -v# 启动nginx
nginx# 查询进程
ps -ef
OPTIONS:
-e 显示所有进程
-f 全格式
访问nginx:
我们通过浏览器,访问部署nginx的机器(默认使用80号端口)。浏览器就会给我们响应Nginx首页 —— 因为其本质就是一个Web服务器。

调整nginx配置:
正如你所言,Nginx是一个Web服务器,那么它响应的代码数据,能够通过浏览器解释渲染出来,那么我们怎么没能看到后台的html文件呢?它又在什么地方?我们可以访问、修改吗?答案是肯定的!
# 配置文件
cd /etc/nginx
我们需要关注,上述标识的两个文件。

打开文件后,我们可以得到这个首页资源,在机器上存放的位置。
# 本系统为Centos8.2 可能其他版本的位置不一样
/usr/share/nginx/html/
在这里,我们可以看到很多有关html的信息,以及一些图片。我们打开 “index.html”,并对其中的一些标签进行修改:

重新进入后,就可以看到展示结果啦~

本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~

相关文章:

nginx服务
“欢唱吧,呼唤它,回来啊~” Web服务器简介 Web服务器,一般是指“网站服务器”,其本质就是驻留于互联网中,某一台机器(计算机)上的进程(程序)。Web服务器通常就是为用户提供信息浏览服务,更可以放置数据文件…...

多数pythoneer只知有列表list却不知道python也有array数组
数组和列表 Python中数组和列表是不同的,我敢断言大多数的pythoneer只知道有列表list,却不知道python也有array数组。列表是一个包含不同数据类型的元素集合,而数组是一个只能含相同数据类型的元素集合。 Python的array库是一个提供数组操作…...
)
【Rust】——控制流(if-else,循环)
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...

通过platform总线驱动框架编写LED灯的驱动,编写应用程序测试
mydev.c #include <linux/init.h> #include <linux/module.h> #include <linux/of_gpio.h> #include <linux/gpio.h> #include <linux/platform_device.h> #include <linux/mod_devicetable.h>// 创建功能码 #define LED_ON _IO(l, 1) #d…...

费舍尔FISHER金属探测器探测仪维修F70
美国FISHER LABS费舍尔地下金属探测器,金属探测仪等维修(考古探金银铜探宝等仪器)。 费舍尔F70视听目标ID金属探测器,Fisher 金属探测器公司成立于1931年,在实验条件很艰苦的情况下,研发出了地下金属探测器…...
Airtest-Selenium实操小课③:下载可爱猫猫图片
1. 前言 那么这周我们看看如何实现使用Airtest-Selenium实现自动搜索下载可爱的猫猫图片吧~ 2. 需求分析和准备 整体的需求大致可以分为以下步骤: 打开chrome浏览器 打开百度网页 搜索“可爱猫猫图片” 定位图片元素 创建存储图片的文件夹 下载可爱猫猫图片…...
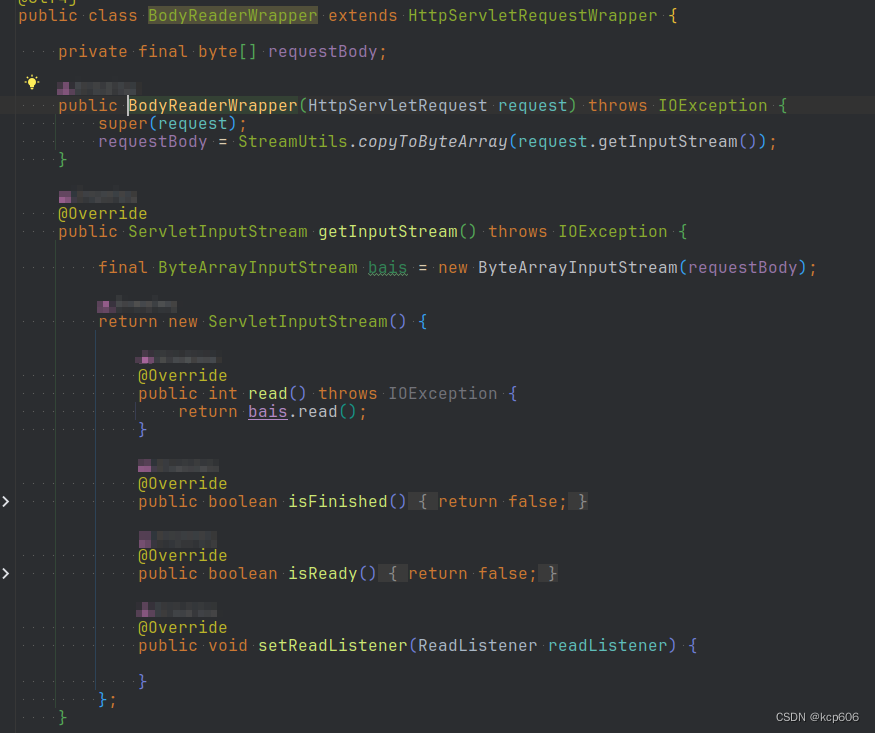
Druid无法登录监控页面
问题表现:在配置和依赖都正确的情况下,无法通过配置的用户名密码登录Druid的监控页面 检查配置发现 配置的用户名和密码和请求中参数是一致的🤔 Debug发现 ResourceServlet 是Druid的登录实现, 且调试发现usernameParam是null&am…...

【Linux系统化学习】深入理解匿名管道(pipe)和命名管道(fifo)
目录 进程间通信 进程间通信目的 进程间通信的方式 管道 System V IPC(本地通信) POSIX IPC(网络通信) 管道 什么是管道 匿名管道 匿名管道的创建 匿名管道的使用 匿名管道的四种情况 匿名管道的五种特性 命名管道 …...

信息学奥赛一本通1209:分数求和
1209:分数求和 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 19111 通过数: 10647 【题目描述】 输入n个分数并对他们求和,并用最简形式表示。所谓最简形式是指:分子分母的最大公约数为11;若最终结果的分母为11&am…...

LabVIEW储氢材料循环寿命测试系统
LabVIEW储氢材料循环寿命测试系统 随着氢能技术的发展,固态储氢技术因其高密度和安全性成为研究热点。储氢材料的循环寿命是衡量其工程应用的关键。然而,传统的循环寿命测试设备存在成本高、测试效率低、数据处理复杂等问题。设计了一种基于LabVIEW软件…...

Unity3D 框架如何搭建基于纯Lua的U框架与开发模式详解
前言 Unity3D 是一款非常流行的游戏开发引擎,它支持C#、JavaScript和Boo等多种脚本语言。而Lua语言作为一种轻量级的脚本语言,也在游戏开发中得到了广泛应用。本文将介绍如何在Unity3D框架中搭建基于纯Lua的U框架,并详细讲解其开发模式。 对…...

Linux常见指令(2)
目录 1、tar指令 ! 2、bc指令 3、uname 4、重要热键 5、关机 1、tar指令 ! 功能:压缩/解压缩文件或目录,类似zip 我们先来看一下我们的文件即目录,接下来我们输入指令: tar -czf test.tgz test 压缩 -c …...

【C++】封装
1.封装的意义 封装是C面向对象三大特性之一 实例化(通过一个类 创建一个对象的过程) 类中的属性和行为 我们统一称为 成员 属性 成员属性 成员变量 行为 成员函数 成员方法 封装的意义: 1.将属性和行为作为一个整体,表现生活中的事…...
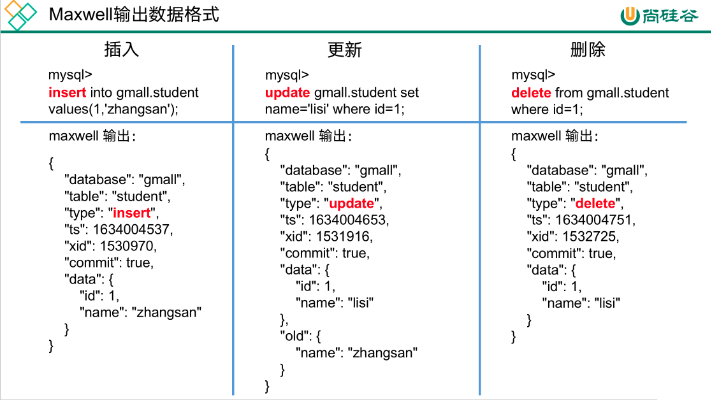
Maxwell安装部署
1 Maxwell输出格式 database:变更数据所属的数据库table:变更数据所属的表type:数据变更类型ts:数据变更发生的时间xid:事务idcommit:事务提交标志,可用于重新组装事务data:对于inse…...
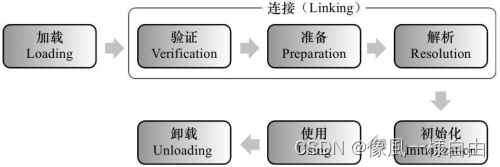
说一下JVM类加载机制?
Java中的所有类,都需要由类加载器装载到JVM中才能运行。类加载器本身也是一个类,而它的工作就是把class文件从硬盘读取到内存中。 在写程序的时候,我们几乎不需要关心类的加载,因为这些都是隐式装载的,除非我们有特殊…...
解决SpringAMQP工作队列模型程序报错:WARN 48068:Failed to declare queue: simple.queue
这里写目录标题 1.运行环境2.报错信息3.解决方案4.查看解决之后的效果 1.运行环境 使用docker运行了RabbitMQ的服务器: 在idea中导入springAMQP的jar包,分别编写了子模块生产者publisher,消费者consumer: 1.在publisher中运行测试…...

mysql在服务器中的主从复制Linux下
mysql在服务器中的主从复制Linux下 为什么要进行主从复制主从复制的原理主从复制执行流程操作步骤主库创建从库创建 测试 为什么要进行主从复制 在业务中通常会有情况,在sql执行时,将表锁住,导致不能进行查询,这样就会影响业务的…...
QT-Day2
思维导图 作业 使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 将登录按钮使用qt5版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin"&#x…...

流量分析——陇剑杯 2021【签到、jwt】
目录 签到1、攻击者正在进行的可能是什么协议的网络攻击 jwt1、该网站使用了______认证方式。前置知识:解: 2、黑客绕过验证使用的jwt中,id和username是3、黑客获取webshell之后,权限是什么4、黑客上传的恶意文件文件名是5、黑客在…...

Java并发基础:原子类之AtomicIntegerFieldUpdater全面解析
本文概要 AtomicIntegerFieldUpdater类提供了一种高效、简洁的方式来原子性地更新对象的volatile字段,无需使用重量级的锁机制,它通过基于反射的API实现了细粒度的并发控制,提升了多线程环境下的性能表现。 AtomicIntegerFieldUpdater核心概…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
