算法沉淀——穷举、暴搜、深搜、回溯、剪枝综合练习四(leetcode真题剖析)

算法沉淀——穷举、暴搜、深搜、回溯、剪枝综合练习四
- 01.解数独
- 02.单词搜索
- 03.黄金矿工
- 04.不同路径 III
01.解数独
题目链接:https://leetcode.cn/problems/sudoku-solver/
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例 1:
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
思路
为了存储每个位置的元素,我们需要定义一个二维数组。首先,我们记录所有已知的数据,然后遍历所有需要处理的位置,并遍历数字1~9。对于每个位置,我们检查该数字是否可以存放在该位置,同时检查行、列和九宫格是否唯一。
我们可以使用一个二维数组来记录每个数字在每一行中是否出现,一个二维数组来记录每个数字在每一列中是否出现。对于九宫格,我们可以以行和列除以3得到的商作为九宫格的坐标,并使用一个三维数组来记录每个数字在每一个九宫格中是否出现。在检查是否存在冲突时,只需检查行、列和九宫格里对应的数字是否已被标记。如果数字至少有一个位置(行、列、九宫格)被标记,则存在冲突,因此不能在该位置放置当前数字。
特别地,在本题中,我们需要直接修改给出的数组,因此在找到一种可行的方法时,应该停止递归,以防止正确的方法被覆盖。
代码
class Solution {bool row[9][10];bool col[9][10];bool grid[3][3][10];
public:void solveSudoku(vector<vector<char>>& board) {for(int i=0;i<9;i++){for(int j=0;j<9;j++){if(board[i][j]!='.'){int num=board[i][j]-'0';row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;}}}dfs(board);}bool dfs(vector<vector<char>>& board){for(int i=0;i<9;i++){for(int j=0;j<9;j++){if(board[i][j]=='.'){for(int num=1;num<=9;num++){if(!row[i][num]&&!col[j][num]&&!grid[i/3][j/3][num]){board[i][j]='0'+num;row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;if(dfs(board)) return true;board[i][j]='.';row[i][num]=col[j][num]=grid[i/3][j/3][num]=false;}}return false;}}}return true;}
};
02.单词搜索
题目链接:https://leetcode.cn/problems/word-search/
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出:true
示例 3:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出:false
提示:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15board和word仅由大小写英文字母组成
思路
其实这里完全就是使用暴力搜索的方式。在解决这个问题时,我们假设每个位置的元素作为第一个字母,然后向相邻的四个方向进行递归,并且不能出现重复使用同一个位置的元素。通过深度优先搜索的方式,不断地枚举相邻元素作为下一个字母出现的可能性,并在递归结束时回溯,直到枚举完所有可能性,得到正确的结果。
代码
class Solution {const int dx[4]={0,0,1,-1};const int dy[4]={-1,1,0,0};int m,n;bool vis[7][7];
public:bool exist(vector<vector<char>>& board, string word) {m=board.size(),n=board[0].size();for(int i=0;i<m;++i){for(int j=0;j<n;++j){if(board[i][j]==word[0]){vis[i][j]=true;if(dfs(board,i,j,word,1)) return true;vis[i][j]=false;}}}return false;}bool dfs(vector<vector<char>>& board, int i,int j,string word,int pos){if(pos==word.size()) return true;for(int k=0;k<4;k++){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&board[x][y]==word[pos]){vis[x][y]=true;if(dfs(board,x,y,word,pos+1)) return true;vis[x][y]=false;}}return false;}
};
03.黄金矿工
题目链接:https://leetcode.cn/problems/path-with-maximum-gold/
你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量;如果该单元格是空的,那么就是 0。
为了使收益最大化,矿工需要按以下规则来开采黄金:
- 每当矿工进入一个单元,就会收集该单元格中的所有黄金。
- 矿工每次可以从当前位置向上下左右四个方向走。
- 每个单元格只能被开采(进入)一次。
- 不得开采(进入)黄金数目为
0的单元格。 - 矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。
示例 1:
输入:grid = [[0,6,0],[5,8,7],[0,9,0]]
输出:24
解释:
[[0,6,0],[5,8,7],[0,9,0]]
一种收集最多黄金的路线是:9 -> 8 -> 7。
示例 2:
输入:grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出:28
解释:
[[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
一种收集最多黄金的路线是:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。
提示:
1 <= grid.length, grid[i].length <= 150 <= grid[i][j] <= 100- 最多 25 个单元格中有黄金。
思路
和上一题的思路基本一致,只不过需添加在对每一次深度遍历时我们记录最大的累加和即可。
代码
class Solution {bool vis[16][16];const int dx[4]={0,0,1,-1};const int dy[4]={-1,1,0,0};int m,n,ret=0;
public:int getMaximumGold(vector<vector<int>>& grid) {m=grid.size(),n=grid[0].size();for(int i=0;i<m;++i){for(int j=0;j<n;++j){if(grid[i][j]){vis[i][j]=true;dfs(grid,i,j,grid[i][j]);vis[i][j]=false;}}}return ret;}void dfs(vector<vector<int>>& grid,int i,int j,int path){ret=max(ret,path);for(int k=0;k<4;++k){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&grid[x][y]){vis[x][y]=true;dfs(grid,x,y,path+grid[x][y]);vis[x][y]=false;}}}
};
04.不同路径 III
题目链接:https://leetcode.cn/problems/unique-paths-iii/
在二维网格 grid 上,有 4 种类型的方格:
1表示起始方格。且只有一个起始方格。2表示结束方格,且只有一个结束方格。0表示我们可以走过的空方格。-1表示我们无法跨越的障碍。
返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目**。**
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
示例 1:
输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出:2
解释:我们有以下两条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2:
输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出:4
解释:我们有以下四条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3:
输入:[[0,1],[2,0]]
输出:0
解释:
没有一条路能完全穿过每一个空的方格一次。
请注意,起始和结束方格可以位于网格中的任意位置。
提示:
1 <= grid.length * grid[0].length <= 20
思路
这里和上面的回溯不太一样的地方在于我们必须通过所有的0标记位置,首先我们要计算出所有0的个数,再加上1个2的位置就是我们要走的路的长度,依照要走的长度和起始位置找到不同的路线,这里可以使用深度优先遍历找到不同的路径。
代码
class Solution {bool vis[21][21];const int dx[4]={0,0,1,-1};const int dy[4]={-1,1,0,0};int m,n,ret=0;
public:int uniquePathsIII(vector<vector<int>>& grid) {m=grid.size(),n=grid[0].size();int count=0,left,right;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==0) count++;else if(grid[i][j]==1){left=i;right=j;}}}vis[left][right]=true;dfs(grid,left,right,count+1);return ret;}void dfs(vector<vector<int>>& grid,int left,int right,int count){if(grid[left][right]==2){if(!count) ret++;return;} for(int k=0;k<4;k++){int x=left+dx[k],y=right+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&grid[x][y]!=-1){vis[x][y]=true;dfs(grid,x,y,count-1);vis[x][y]=false;}}}
};
相关文章:

算法沉淀——穷举、暴搜、深搜、回溯、剪枝综合练习四(leetcode真题剖析)
算法沉淀——穷举、暴搜、深搜、回溯、剪枝综合练习四 01.解数独02.单词搜索03.黄金矿工04.不同路径 III 01.解数独 题目链接:https://leetcode.cn/problems/sudoku-solver/ 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则&am…...

如何在java中使用 Excel 动态函数生成依赖列表
前言 在Excel 中,依赖列表或级联下拉列表表示两个或多个列表,其中一个列表的项根据另一个列表而变化。依赖列表通常用于Excel的业务报告,例如学术记分卡中的【班级-学生】列表、区域销售报告中的【区域-国家/地区】列表、人口仪表板中的【年…...

07 MyBatis之高级映射 + 懒加载(延迟加载)+缓存
1. 高级映射 例如有两张表, 分别为班级表和学生表 自然, 一个班级对应多个学生 像这种数据 , 应该如果如何映射到Java的实体类上呢? 这就是高级映射解决的问题 以班级和学生为例子 , 因为一个班级对应多个学生 , 因此学生表中必定有一个班级编号字段cid 但我们在学生的实体…...

MT8791迅鲲900T联发科5G安卓核心板规格参数_MTK平台方案定制
MT8791安卓核心板是一款搭载了旗舰级配置的中端手机芯片。该核心板采用了八核CPU架构设计,但是升级了旗舰级的Arm Cortex-A78核心,两个大核主频最高可达2.4GHz。配备了Arm Mali-G68 GPU,通过Mali-G88的先进技术,图形处理性能大幅提…...

java:Java中的数组详解
目录 Java数组的定义和特点: Java数组的初始化和赋值 Java数组的常用操作 1. 遍历数组 2. 获取数组长度 3. 访问数组元素 4. 数组的拷贝 多维数组 数组的排序和查找 冒泡排序: 快速排序 : 二分查找: 数组的应用: Java数…...

Modern C++ std::visit从实践到原理
前言 std::visit 是 C17 中引入的一个模板函数,它用于对给定的 variant、union 类型或任何其他兼容的类型执行一个访问者操作。这个函数为多种可能类型的值提供了一种统一的访问机制。使用 std::visit,你可以编写更通用和灵活的代码,而无需关…...

谷歌gemma2b windows本地cpu gpu部署,pytorch框架,模型文件百度网盘下载
简介 谷歌DeepMind发布了Gemma,这是一系列灵感来自用于Gemini相同研究和技术的开放模型。开放模型适用于各种用例,这是谷歌非常明智的举措。有2B(在2T tokens上训练)和7B(在6T tokens上训练)模型,包括基础和指令调整版本。在8192个token的上下文长度上进行训练。允许商业使…...
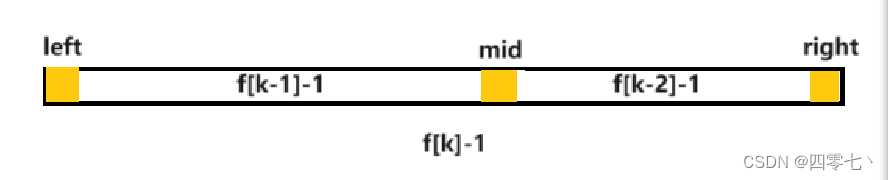
数据结构-查找与排序
数据结构再往后就是比较零散的各种操作,查找与排序是其中最常出现的,今天来总结一下常用的查找与排序所用的方法 查找 顺序查找 最简单的查找方式,遍历,然后比较 bool search1(int *a,int n,int k){for (int i1;i<n;i){//遍…...
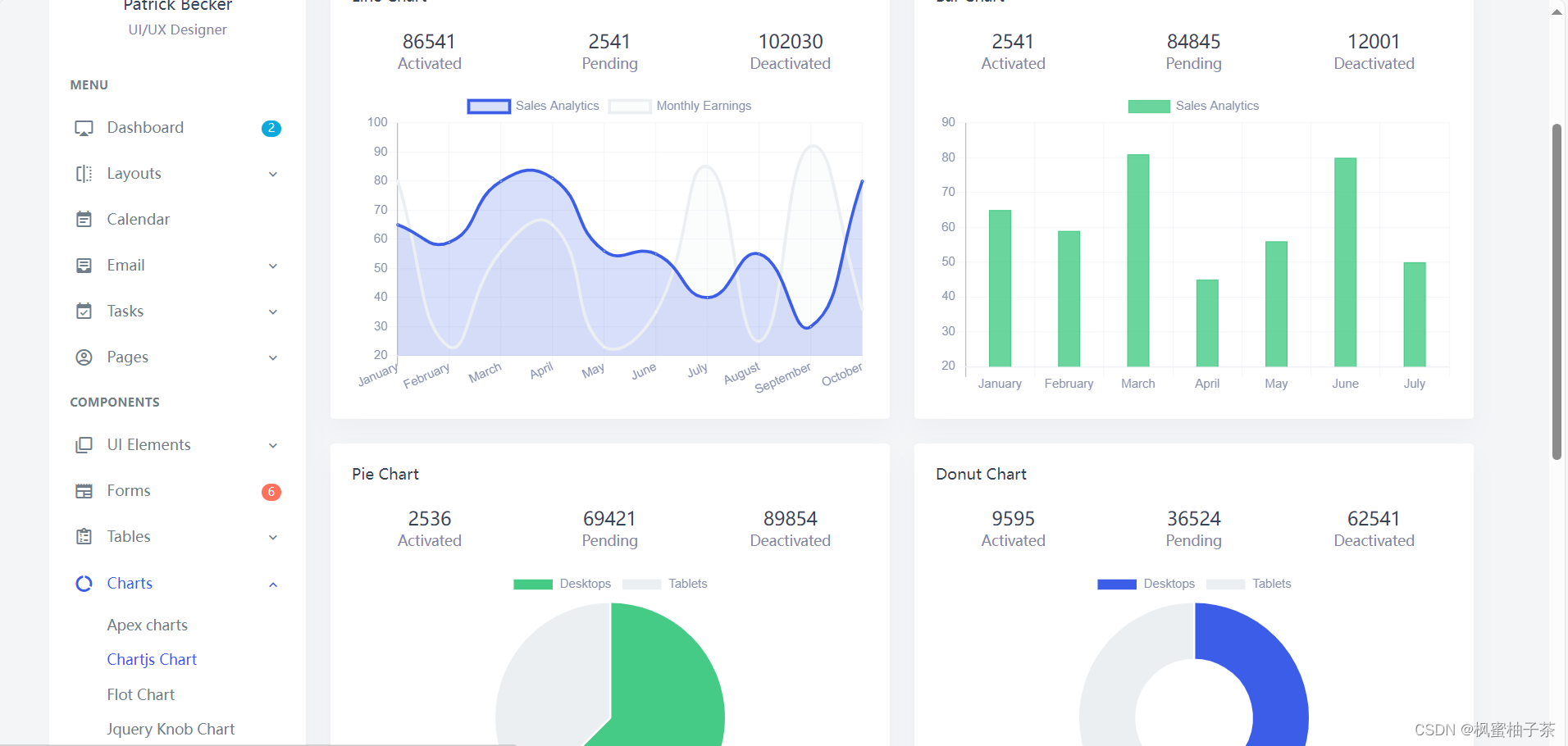
【前端素材】推荐优质后台管理系统Qovex平台模板(附源码)
一、需求分析 1、定义 后台管理系统是一种用于管理和监控网站、应用程序或系统的在线工具。它通常是通过网页界面进行访问和操作,用于管理网站内容、用户权限、数据分析等。后台管理系统是网站或应用程序的控制中心,管理员可以通过后台系统进行各种管理…...
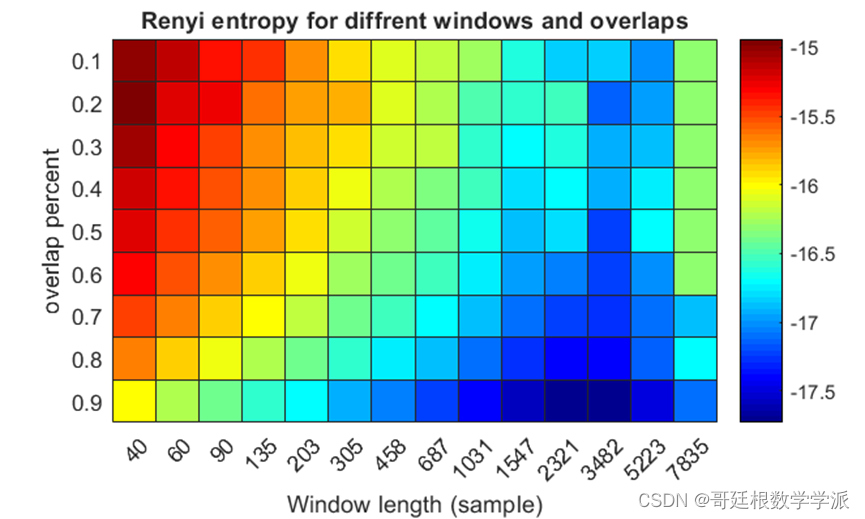
MATLAB环境下基于短时傅里叶变换和Rényi熵的脑电信号和语音信号分析
傅里叶变换是不能很好的反映信号在时域的某一个局部范围的频谱特点的,这一点很可惜。因为在许多实际工程中,人们对信号在局部区域的特征是比较关心的,这些特征包含着十分有用的信息。这类信号因为在时域(或者是空间域)上具有突变的非稳定性和…...

Go语言调用身份证实名认证API方法-标准版身份证实名认证接口
翔云身份证实名认证接口具备高准确度的身份信息比对能力,包括姓名、身份证号码、人脸照片等信息的一致性验证,并能实时反馈验证结果。 以下是GO语言调用翔云身份实名认证API的代码: package mainimport ("fmt""bytes"&q…...

数据库增删改查
DDL: 数据定义语言,用来定义数据库对象(数据库、表、字段)DML: 数据操作语言,用来对数据库表中的数据进行增删改DQL: 数据查询语言,用来查询数据库中表的记录DCL: 数据控制语言,用来创建数据库用户、控制数…...

10.CSS3的calc函数
CSS3 的 calc 函数 经典真题 CSS 的计算属性知道吗? CSS3 中的 calc 函数 calc 是英文单词 calculate(计算)的缩写,是 CSS3 的一个新增的功能。 MDN 的解释为可以用在任何长度、数值、时间、角度、频率等处,语法如…...
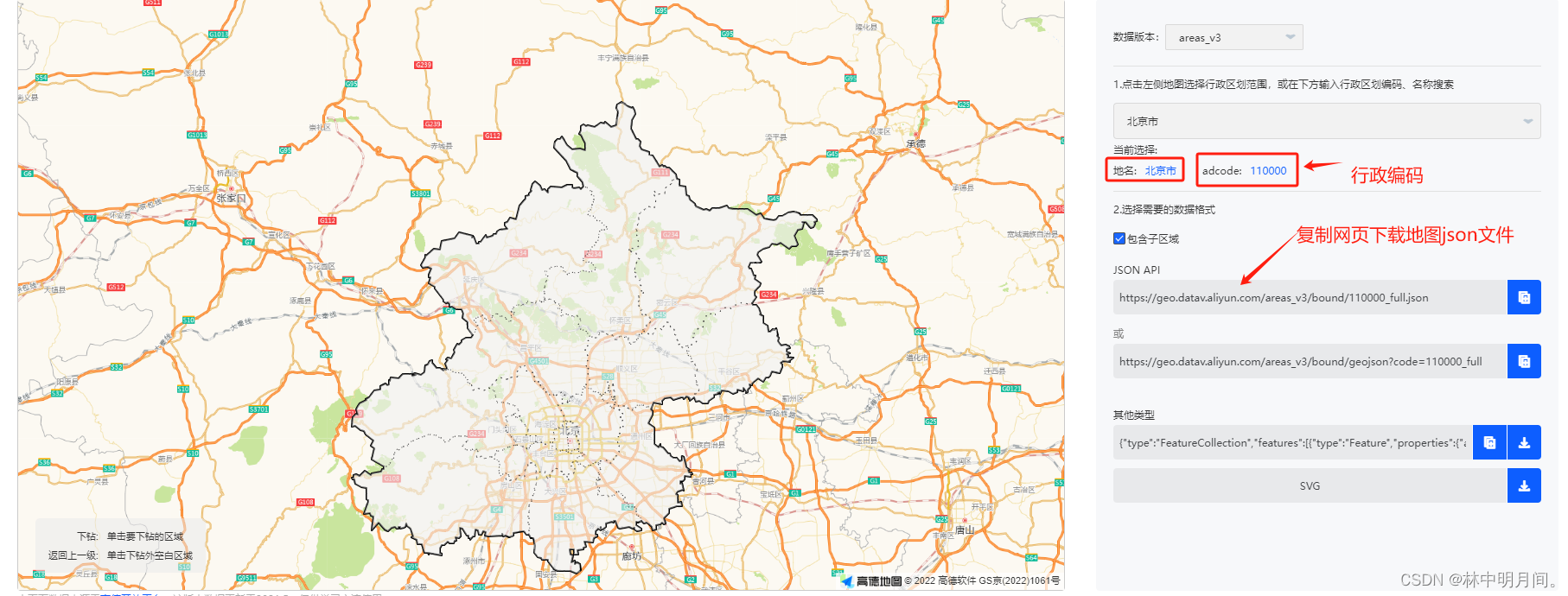
echrts 全国地图、各省市地图json文件下载
DataV.GeoAtlas地理小工具系列...

如何使用1688.item_search_shop API获取阿里巴巴店铺商品信息
要使用1688的item_search_shop API获取阿里巴巴店铺的商品信息,你通常需要遵循以下步骤: 1. 注册并获取API密钥 首先,你需要在阿里巴巴开放平台(如1688开放平台)上注册一个开发者账号,并创建一个应用。创…...

PLC_博图系列☞基本指令“取反RLO”
PLC_博图系列☞基本指令“取反RLO” 文章目录 PLC_博图系列☞基本指令“取反RLO”背景介绍取反RLO说明示例 关键字: PLC、 西门子、 博图、 Siemens 、 取反RLO 背景介绍 这是一篇关于PLC编程的文章,特别是关于西门子的博图软件。我并不是专业的PLC…...

docker安装PostGIS扩展
去docker仓库查找你想要安装的镜像版本,并pull下来 我下载的版本: [rootlocalhost ~]# docker pull postgis/postgis:12-3.2运行容器 [rootlocalhost ~]# docker run --name postgis --privilegedtrue --restartalways -e POSTGRES_USER12345678 -e P…...
LabVIEW开发FPGA的高速并行视觉检测系统
LabVIEW开发FPGA的高速并行视觉检测系统 随着智能制造的发展,视觉检测在生产线中扮演着越来越重要的角色,尤其是在质量控制方面。传统的基于PLC的视觉检测系统受限于处理速度和准确性,难以满足当前生产需求的高速和高精度要求。为此…...

P5734 【深基6.例6】文字处理软件 - Java
题目描述 你需要开发一款文字处理软件。最开始时输入一个字符串作为初始文档。可以认为文档开头是第 00 个字符。需要支持以下操作: 1 str:后接插入,在文档后面插入字符串 strstr,并输出文档的字符串;2 a bÿ…...

关于设备连接有人云的使用及modbus rtu协议,服务器端TCP调试设置
有人云调试 调试过程问题1. 关于modbus rtu协议,实质上有三种modbus基本原理modbus 格式2. 关于modbus crc16通信校验3. 关于在ubuntu阿里云服务器端,监听网络数据之调试mNetAssist4. 使用有人FAE传给的设置软件问题???之前的一个项目,再拿出来回顾下。 调试过程 先 要在有…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...
