多传感器融合定位十-基于滤波的融合方法Ⅰ其二
多传感器融合定位十-基于滤波的融合方法Ⅰ其二
- 3. 滤波器基本原理
- 3.1 状态估计模型
- 3.2 贝叶斯滤波
- 3.3 卡尔曼滤波(KF)推导
- 3.4 扩展卡尔曼滤波(EKF)推导
- 3.5 迭代扩展卡尔曼滤波(IEKF)推导
- 4. 基于滤波器的融合
- 4.1 状态方程
- 4.2 观测方程
- 4.3 构建滤波器
- 4.4 Kalman 滤波实际使用流程
- 4.4.1 位姿初始化
- 4.4.2 Kalman 初始化
- 4.4.3 惯性解算
- 4.4.4 Kalman 预测更新
- 4.4.5 无观测时后验更新
- 4.4.6 有观测时的量测更新
- 4.4.7 有观测时计算后验位姿
- 4.4.8 有观测时状态量清零
- 4.4.9 输出位姿
Reference:
- 深蓝学院-多传感器融合
- 多传感器融合定位理论基础
文章跳转:
- 多传感器融合定位一-3D激光里程计其一:ICP
- 多传感器融合定位二-3D激光里程计其二:NDT
- 多传感器融合定位三-3D激光里程计其三:点云畸变补偿
- 多传感器融合定位四-3D激光里程计其四:点云线面特征提取
- 多传感器融合定位五-点云地图构建及定位
- 多传感器融合定位六-惯性导航原理及误差分析
- 多传感器融合定位七-惯性导航解算及误差分析其一
- 多传感器融合定位八-惯性导航解算及误差分析其二
- 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
- 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
- 多传感器融合定位十一-基于滤波的融合方法Ⅱ
- 多传感器融合定位十二-基于图优化的建图方法其一
- 多传感器融合定位十三-基于图优化的建图方法其二
- 多传感器融合定位十四-基于图优化的定位方法
- 多传感器融合定位十五-多传感器时空标定(综述)
3. 滤波器基本原理
3.1 状态估计模型
实际状态估计任务中,待估计的后验概率密度可以表示为:
p(xk∣xˇ0,v1:k,y0:k)p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k}\right) p(xk∣xˇ0,v1:k,y0:k)其中:
xˇ0\check{\boldsymbol{x}}_0xˇ0 表示的是状态初始值
v1:k\boldsymbol{v}_{1: k}v1:k 表示从 111 到 kkk 时刻的输入
y0:k\boldsymbol{y}_{0: k}y0:k 表示从 000 到 kkk 时刻的观测
因此,滤波问题可以直观表示为,根据所有历史数据(输入、观测、初始状态)得出最终的融合结果。
历史数据之间的关系,可以用下面的图模型表示,
 图模型中体现了
图模型中体现了马尔可夫性,即当前状态只跟前一时刻状态相关,和其他历史时刻状态无关。
该性质的数学表达:
运动方程:xk=f(xk−1,vk,wk)\boldsymbol{x}_k=\boldsymbol{f}\left(\boldsymbol{x}_{k-1}, \boldsymbol{v}_k, \boldsymbol{w}_k\right)xk=f(xk−1,vk,wk)
观测方程:yk=g(xk,nk)\boldsymbol{y}_k=\boldsymbol{g}\left(\boldsymbol{x}_k, \boldsymbol{n}_k\right)yk=g(xk,nk)
3.2 贝叶斯滤波
公式的推导可参考:非线性优化
根据贝叶斯公式,kkk 时刻后验概率密度可以表示为:
p(xk∣xˇ0,v1:k,y0:k)=p(yk∣xk,xˇ0,v1:k,y0:k−1)p(xk∣xˇ0,v1:k,y0:k−1)p(yk∣xˇ0,v1:k,y0:k−1)=ηp(yk∣xk,xˇ0,v1:k,y0:k−1)p(xk∣xˇ0,v1:k,y0:k−1)\begin{aligned} p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k}\right) & =\frac{p\left(\boldsymbol{y}_k \mid \boldsymbol{x}_k, \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right)}{p\left(\boldsymbol{y}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right)} \\ & =\eta p\left(\boldsymbol{y}_k \mid \boldsymbol{x}_k, \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) \end{aligned} p(xk∣xˇ0,v1:k,y0:k)=p(yk∣xˇ0,v1:k,y0:k−1)p(yk∣xk,xˇ0,v1:k,y0:k−1)p(xk∣xˇ0,v1:k,y0:k−1)=ηp(yk∣xk,xˇ0,v1:k,y0:k−1)p(xk∣xˇ0,v1:k,y0:k−1)(这里 yk\boldsymbol{y_k}yk 是当前时刻的观测,而 p(xk∣xˇ0,v1:k,y0:k)p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k}\right)p(xk∣xˇ0,v1:k,y0:k) 是当前时刻后验,p(xk∣xˇ0,v1:k,y0:k−1)p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right)p(xk∣xˇ0,v1:k,y0:k−1)为先验。我们需要的是后验概率最大化,因为贝叶斯分母部分与待估计的状态无关,因而可以忽略)
根据观测方程, yk\boldsymbol{y}_kyk 只和 xk\boldsymbol{x}_kxk 相关,因此上式可以简写为:
p(xk∣xˇ0,v1:k,y0:k)=ηp(yk∣xk)p(xk∣xˇ0,v1:k,y0:k−1)p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k}\right)=\eta p\left(\boldsymbol{y}_k \mid \boldsymbol{x}_k\right) p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) p(xk∣xˇ0,v1:k,y0:k)=ηp(yk∣xk)p(xk∣xˇ0,v1:k,y0:k−1)利用条件分布的性质,可得:
p(xk∣xˇ0,v1:k,y0:k−1)=∫p(xk∣xk−1,xˇ0,v1:k,y0:k−1)p(xk−1∣xˇ0,v1:k,y0:k−1)dxk−1\begin{aligned} & p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) \\ & =\int p\left(\boldsymbol{x}_k \mid \boldsymbol{x}_{k-1}, \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) p\left(\boldsymbol{x}_{k-1} \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \end{aligned} p(xk∣xˇ0,v1:k,y0:k−1)=∫p(xk∣xk−1,xˇ0,v1:k,y0:k−1)p(xk−1∣xˇ0,v1:k,y0:k−1)dxk−1再利用马尔可夫性,可得:
p(xk∣xˇ0,v1:k,y0:k−1)=∫p(xk∣xk−1,vk)p(xk−1∣xˇ0,v1:k,y0:k−1)dxk−1\begin{aligned} & p\left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) \\ & =\int p\left(\boldsymbol{x}_k \mid \boldsymbol{x}_{k-1}, \boldsymbol{v}_k\right) p\left(\boldsymbol{x}_{k-1} \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \end{aligned} p(xk∣xˇ0,v1:k,y0:k−1)=∫p(xk∣xk−1,vk)p(xk−1∣xˇ0,v1:k,y0:k−1)dxk−1经过以上化简,最终后验概率可以写为:

根据以上结果,可以画出贝叶斯滤波的信息流图如下:

贝叶斯滤波是一个非常广泛的概念,它不特指某一种滤波:

- 在高斯假设前提下,用贝叶斯滤波的原始形式推导比较复杂,可以利用高斯的特征得到简化形式,即广义高斯滤波。后面 KF、EKF、IEKF 的推导均采用这种形式。
- 实际中,UKF 和 PF 多应用于扫地机器人等2D小场景,与本课程目标场景不符,因此不做讲解。(UKF 和 PF 本身有一个维度的问题,维度高了不太行,而我们这里使用的维度多半是15维的,在三维场景就不好用了)
3.3 卡尔曼滤波(KF)推导
在线性高斯假设下,上式可以重新写为下面的形式(为了和后面符号对应)
运动方程: xk=F(xk−1,vk)+Bk−1wk\boldsymbol{x}_k=\boldsymbol{F}\left(\boldsymbol{x}_{k-1}, \boldsymbol{v}_k\right)+\boldsymbol{B}_{k-1} \boldsymbol{w}_kxk=F(xk−1,vk)+Bk−1wk
观测方程: yk=G(xk)+Cknk\boldsymbol{y}_k=\boldsymbol{G}\left(\boldsymbol{x}_k\right)+\boldsymbol{C}_k \boldsymbol{n}_kyk=G(xk)+Cknk
(F\boldsymbol{F}F 和 G\boldsymbol{G}G 在这里代表的是线性的意思,非线性是后面要推导的。这里的 G\boldsymbol{G}G 和之前卡尔曼文章里写的 H\boldsymbol{H}H 是一个东西。n\boldsymbol{n}n 为观测噪声,是个零均值白噪声)
把上一时刻的后验状态写为:
p(xk−1∣xˇ0,v1:k−1,y0:k−1)=N(x^k−1,P^k−1)p\left(\boldsymbol{x}_{k-1} \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k-1}, \boldsymbol{y}_{0: k-1}\right)=\mathcal{N}\left(\hat{\boldsymbol{x}}_{k-1}, \hat{\boldsymbol{P}}_{k-1}\right) p(xk−1∣xˇ0,v1:k−1,y0:k−1)=N(x^k−1,P^k−1)则当前时刻的预测值为:
xˇk=F(x^k−1,vk)\check{\boldsymbol{x}}_k=\boldsymbol{F}\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_k\right) xˇk=F(x^k−1,vk)根据高斯分布的线性变化,它的方差为(可仿照第2.8节中的推导过程自行推导):
Pˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1T\check{\boldsymbol{P}}_k=\boldsymbol{F}_{k-1} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k-1}^{\mathrm{T}}+\boldsymbol{B}_{k-1} \boldsymbol{Q}_k \boldsymbol{B}_{k-1}^{\mathrm{T}} Pˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1T其中 QkQ_kQk 为当前输入噪声的方差。
若把 kkk 时刻状态和观测的联合高斯分布写为:
p(xk,yk∣xˇ0,v1:k,y0:k−1)=N([μx,kμy,k],[Σxx,kΣxy,kΣyx,kΣyy,k])p\left(\boldsymbol{x}_k, \boldsymbol{y}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right)=\mathcal{N}\left(\left[\begin{array}{c} \boldsymbol{\mu}_{x, k} \\ \boldsymbol{\mu}_{y, k} \end{array}\right],\left[\begin{array}{cc} \boldsymbol{\Sigma}_{x x, k} & \boldsymbol{\Sigma}_{x y, k} \\ \boldsymbol{\Sigma}_{y x, k} & \boldsymbol{\Sigma}_{y y, k} \end{array}\right]\right) p(xk,yk∣xˇ0,v1:k,y0:k−1)=N([μx,kμy,k],[Σxx,kΣyx,kΣxy,kΣyy,k])根据第2.7节中的推导结果, kkk 时刻的后验概率可以写为:
p(xk∣xˇ0,v1:k,y0:k)=N(μx,k+Σxy,kΣyy,k−1(yk−μy,k)⏟x^k,Σxx,k−Σxy,kΣyy,k−1Σyx,k⏟P^k)\begin{aligned} p & \left(\boldsymbol{x}_k \mid \check{\boldsymbol{x}}_0, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k}\right) \\ & =\mathcal{N}(\underbrace{\boldsymbol{\mu}_{x, k}+\boldsymbol{\Sigma}_{x y, k} \boldsymbol{\Sigma}_{y y, k}^{-1}\left(\boldsymbol{y}_k-\boldsymbol{\mu}_{y, k}\right)}_{\hat{\boldsymbol{x}}_k}, \underbrace{\boldsymbol{\Sigma}_{x x, k}-\boldsymbol{\Sigma}_{x y, k} \boldsymbol{\Sigma}_{y y, k}^{-1} \boldsymbol{\Sigma}_{y x, k}}_{\hat{P}_k}) \end{aligned} p(xk∣xˇ0,v1:k,y0:k)=N(x^kμx,k+Σxy,kΣyy,k−1(yk−μy,k),P^kΣxx,k−Σxy,kΣyy,k−1Σyx,k)其中 x^k\hat{\boldsymbol{x}}_kx^k 和 P^k\hat{\boldsymbol{P}}_kP^k 分别为后验均值和方差。若定义:
Kk=Σxy,kΣyy,k−1\boldsymbol{K}_k=\boldsymbol{\Sigma}_{x y, k} \boldsymbol{\Sigma}_{y y, k}^{-1} Kk=Σxy,kΣyy,k−1则有:
P^k=Pˇk−KkΣxy,kTx^k=xˇk+Kk(yk−μy,k)\begin{aligned} & \hat{\boldsymbol{P}}_k=\check{\boldsymbol{P}}_k-\boldsymbol{K}_k \boldsymbol{\Sigma}_{x y, k}^{\mathrm{T}} \\ & \hat{\boldsymbol{x}}_k=\check{\boldsymbol{x}}_k+\boldsymbol{K}_k\left(\boldsymbol{y}_k-\boldsymbol{\mu}_{y, k}\right) \end{aligned} P^k=Pˇk−KkΣxy,kTx^k=xˇk+Kk(yk−μy,k)把第2.8节中的推导得出的线性变换后的均值、方差及交叉项带入上面的式子,可以得到:
Kk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1P^k=(1−KkGk)Pˇkx^k=xˇk+Kk(yk−G(xˇk))\begin{aligned} \boldsymbol{K}_k & =\check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}\left(\boldsymbol{G}_k \check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}+\boldsymbol{C}_k \boldsymbol{R}_k \boldsymbol{C}_k^{\mathrm{T}}\right)^{-1} \\ \hat{\boldsymbol{P}}_k & =\left(\mathbf{1}-\boldsymbol{K}_k \boldsymbol{G}_k\right) \check{\boldsymbol{P}}_k \\ \hat{\boldsymbol{x}}_k & =\check{\boldsymbol{x}}_k+\boldsymbol{K}_k\left(\boldsymbol{y}_k-\boldsymbol{G}\left(\check{\boldsymbol{x}}_k\right)\right) \end{aligned} KkP^kx^k=PˇkGkT(GkPˇkGkT+CkRkCkT)−1=(1−KkGk)Pˇk=xˇk+Kk(yk−G(xˇk))上面方程与之前所述预测方程(如下),就构成了卡尔曼经典五个方程。
xˇk=F(x^k−1,vk)Pˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1T\begin{gathered} \check{\boldsymbol{x}}_k=\boldsymbol{F}\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_k\right) \\ \check{\boldsymbol{P}}_k=\boldsymbol{F}_{k-1} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k-1}^{\mathrm{T}}+\boldsymbol{B}_{k-1} \boldsymbol{Q}_k \boldsymbol{B}_{k-1}^{\mathrm{T}} \end{gathered} xˇk=F(x^k−1,vk)Pˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1T需要说明的是,若不把第2.8节中的结果带入,而保留上页的原始形式,则对应的五个方程被称为广义高斯滤波。
3.4 扩展卡尔曼滤波(EKF)推导
当运动方程或观测方程为非线性的时候,无法再利用之前所述的线性变化关系进行推导,常用的解决方法是进行线性化,把非线性方程一阶泰勒展开成线性。即:
运动方程: xk=f(xk−1,vk,wk)≈xˇk+Fk−1(xk−1−x^k−1)+Bk−1wk\boldsymbol{x}_k=\boldsymbol{f}\left(\boldsymbol{x}_{k-1}, \boldsymbol{v}_k, \boldsymbol{w}_k\right) \approx \check{\boldsymbol{x}}_k+\boldsymbol{F}_{k-1}\left(\boldsymbol{x}_{k-1}-\hat{\boldsymbol{x}}_{k-1}\right)+\boldsymbol{B}_{k-1} \boldsymbol{w}_kxk=f(xk−1,vk,wk)≈xˇk+Fk−1(xk−1−x^k−1)+Bk−1wk
观测方程: yk=g(xk,nk)≈yˇk+Gk(xk−xˇk)+Cknk\boldsymbol{y}_k=\boldsymbol{g}\left(\boldsymbol{x}_k, \boldsymbol{n}_k\right) \approx \check{\boldsymbol{y}}_k+\boldsymbol{G}_k\left(\boldsymbol{x}_k-\check{\boldsymbol{x}}_k\right)+\boldsymbol{C}_k \boldsymbol{n}_kyk=g(xk,nk)≈yˇk+Gk(xk−xˇk)+Cknk
其中
xˇk=f(x^k−1,vk,0)yˇk=g(xˇk,0)Fk−1=∂f(xk−1,vk,wk)∂xk−1∣x^k−1,vk,0Gk=∂g(xk,nk)∂xk∣xˇk,0Bk−1=∂f(xk−1,vk,wk)∂wk∣x^k−1,vk,0Ck=∂g(xk,nk)∂nk∣xˇk,0\begin{array}{ll} \check{\boldsymbol{x}}_k=\boldsymbol{f}\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_k, \mathbf{0}\right) & \check{\boldsymbol{y}}_k=\boldsymbol{g}\left(\check{\boldsymbol{x}}_k, \mathbf{0}\right) \\ \boldsymbol{F}_{k-1}=\left.\frac{\partial \boldsymbol{f}\left(\boldsymbol{x}_{k-1}, \boldsymbol{v}_k, \boldsymbol{w}_k\right)}{\partial \boldsymbol{x}_{k-1}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_k, \mathbf{0}} & \boldsymbol{G}_k=\left.\frac{\partial \boldsymbol{g}\left(\boldsymbol{x}_k, \boldsymbol{n}_k\right)}{\partial \boldsymbol{x}_k}\right|_{\check{\boldsymbol{x}}_k, \mathbf{0}} \\ \boldsymbol{B}_{k-1}=\left.\frac{\partial \boldsymbol{f}\left(\boldsymbol{x}_{k-1}, \boldsymbol{v}_k, \boldsymbol{w}_k\right)}{\partial \boldsymbol{w}_k}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_k, \mathbf{0}} & \boldsymbol{C}_k=\left.\frac{\partial \boldsymbol{g}\left(\boldsymbol{x}_k, \boldsymbol{n}_k\right)}{\partial \boldsymbol{n}_k}\right|_{\check{\boldsymbol{x}}_k, \mathbf{0}} \end{array} xˇk=f(x^k−1,vk,0)Fk−1=∂xk−1∂f(xk−1,vk,wk)x^k−1,vk,0Bk−1=∂wk∂f(xk−1,vk,wk)x^k−1,vk,0yˇk=g(xˇk,0)Gk=∂xk∂g(xk,nk)xˇk,0Ck=∂nk∂g(xk,nk)xˇk,0根据该线性化展开结果,可以得到预测状态的统计学特征为
E[xk]≈xˇk+Fk−1(xk−1−x^k−1)+E[Bk−1wk]⏟0E[(xk−E[xk])(xk−E[xk])T]≈E[Bk−1wkwTTBk−1T]⏟Bk−1QkBk−1T\begin{aligned} & E\left[\boldsymbol{x}_k\right] \approx \check{\boldsymbol{x}}_k+\boldsymbol{F}_{k-1}\left(\boldsymbol{x}_{k-1}-\hat{\boldsymbol{x}}_{k-1}\right)+\underbrace{E\left[\boldsymbol{B}_{k-1} \boldsymbol{w}_k\right]}_0 \\ & E\left[\left(\boldsymbol{x}_k-E\left[\boldsymbol{x}_k\right]\right)\left(\boldsymbol{x}_k-E\left[\boldsymbol{x}_k\right]\right)^{\mathrm{T}}\right] \approx \underbrace{E\left[\boldsymbol{B}_{k-1} \boldsymbol{w}_k \boldsymbol{w}_{\mathrm{T}}^{\mathrm{T}} \boldsymbol{B}_{k-1}^{\mathrm{T}}\right]}_{\boldsymbol{B}_{k-1} \boldsymbol{Q}_k \boldsymbol{B}_{k-1}^{\mathrm{T}}} \end{aligned} E[xk]≈xˇk+Fk−1(xk−1−x^k−1)+0E[Bk−1wk]E[(xk−E[xk])(xk−E[xk])T]≈Bk−1QkBk−1TE[Bk−1wkwTTBk−1T]即 p(xk∣xk−1,vk)≈N(xˇk+Fk−1(xk−1−x^k−1),Bk−1QkBk−1T)p\left(\boldsymbol{x}_k \mid \boldsymbol{x}_{k-1}, \boldsymbol{v}_k\right) \approx \mathcal{N}\left(\check{\boldsymbol{x}}_k+\boldsymbol{F}_{k-1}\left(\boldsymbol{x}_{k-1}-\hat{\boldsymbol{x}}_{k-1}\right), \boldsymbol{B}_{k-1} \boldsymbol{Q}_k \boldsymbol{B}_{k-1}^{\mathrm{T}}\right)p(xk∣xk−1,vk)≈N(xˇk+Fk−1(xk−1−x^k−1),Bk−1QkBk−1T)
同理,可得到观测的统计学特征为:
E[yk]≈yˇk+Gk(xk−xˇk)+E[Cknk]⏟0E[(yk−E[yk])(yk−E[yk])T]≈E[CknknkTCkT]⏟CkRkCkT\begin{aligned} & E\left[\boldsymbol{y}_k\right] \approx \check{\boldsymbol{y}}_k+\boldsymbol{G}_k\left(\boldsymbol{x}_k-\check{\boldsymbol{x}}_k\right)+\underbrace{E\left[\boldsymbol{C}_k \boldsymbol{n}_k\right]}_0 \\ & E\left[\left(\boldsymbol{y}_k-E\left[\boldsymbol{y}_k\right]\right)\left(\boldsymbol{y}_k-E\left[\boldsymbol{y}_k\right]\right)^{\mathrm{T}}\right] \approx \underbrace{E\left[\boldsymbol{C}_k \boldsymbol{n}_k \boldsymbol{n}_k^{\mathrm{T}} \boldsymbol{C}_k^{\mathrm{T}}\right]}_{C_k \boldsymbol{R}_k \boldsymbol{C}_k^{\mathrm{T}}} \end{aligned} E[yk]≈yˇk+Gk(xk−xˇk)+0E[Cknk]E[(yk−E[yk])(yk−E[yk])T]≈CkRkCkTE[CknknkTCkT]即 p(yk∣xk)≈N(yˇk+Gk(xk−xˇk),CkRkCkT)p\left(\boldsymbol{y}_k \mid \boldsymbol{x}_k\right) \approx \mathcal{N}\left(\check{\boldsymbol{y}}_k+\boldsymbol{G}_k\left(\boldsymbol{x}_k-\check{\boldsymbol{x}}_k\right), \boldsymbol{C}_k \boldsymbol{R}_k \boldsymbol{C}_k^{\mathrm{T}}\right)p(yk∣xk)≈N(yˇk+Gk(xk−xˇk),CkRkCkT)
把均值和方差的具体形式,带入广义高斯滤波的公式,最终得到 EKF 下得经典五个公式。
Pˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1Txˇk=f(x^k−1,vk,0)Kk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1P^k=(I−KkGk)Pˇkx^k=xˇk+Kk(yk−g(xˇk,0))\begin{aligned} & \check{\boldsymbol{P}}_k=\boldsymbol{F}_{k-1} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k-1}^{\mathrm{T}}+\boldsymbol{B}_{k-1} \boldsymbol{Q}_k \boldsymbol{B}_{k-1}^{\mathrm{T}} \\ & \check{\boldsymbol{x}}_k=\boldsymbol{f}\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_k, \mathbf{0}\right) \\ & \boldsymbol{K}_k=\check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}\left(\boldsymbol{G}_k \check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}+\boldsymbol{C}_k \boldsymbol{R}_k \boldsymbol{C}_k^{\mathrm{T}}\right)^{-1} \\ & \hat{\boldsymbol{P}}_k=\left(\mathbf{I}-\boldsymbol{K}_k \boldsymbol{G}_k\right) \check{\boldsymbol{P}}_k \\ & \hat{\boldsymbol{x}}_k=\check{\boldsymbol{x}}_k+\boldsymbol{K}_k\left(\boldsymbol{y}_k-\boldsymbol{g}\left(\check{\boldsymbol{x}}_k, \mathbf{0}\right)\right) \end{aligned} Pˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1Txˇk=f(x^k−1,vk,0)Kk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1P^k=(I−KkGk)Pˇkx^k=xˇk+Kk(yk−g(xˇk,0))
3.5 迭代扩展卡尔曼滤波(IEKF)推导
由于非线性模型中做了线性化近似,当非线性程度越强时,误差就会较大。但是,由于线性化的工作点离真值越近,线性化的误差就越小,因此解决该问题的一个方法是,通过迭代逐渐找到准确的线性化点,从而提高精度。
在EKF的推导中,其他保持不变,仅改变观测的线性化工作点,则有:
g(xk,nk)≈yop,k+Gk(xk−xop,k)+Cknk\boldsymbol{g}\left(\boldsymbol{x}_k, \boldsymbol{n}_k\right) \approx \boldsymbol{y}_{\mathrm{op}, k}+\boldsymbol{G}_k\left(\boldsymbol{x}_k-\boldsymbol{x}_{\mathrm{op}, k}\right)+\boldsymbol{C}_k \boldsymbol{n}_k g(xk,nk)≈yop,k+Gk(xk−xop,k)+Cknk其中:
yop,k=g(xop,k,0)Gk=∂g(xk,nk)∂xk∣xop,k,0Ck=∂g(xk,nk)∂nk∣xop,k,0\begin{aligned} & \boldsymbol{y}_{\mathrm{op}, k}=\boldsymbol{g}\left(\boldsymbol{x}_{\mathrm{op}, k}, \mathbf{0}\right) \\ & \boldsymbol{G}_k=\left.\frac{\partial \boldsymbol{g}\left(\boldsymbol{x}_k, \boldsymbol{n}_k\right)}{\partial \boldsymbol{x}_k}\right|_{\boldsymbol{x}_{\mathrm{op}, k}, \mathbf{0}} \\ & \boldsymbol{C}_k=\left.\frac{\partial \boldsymbol{g}\left(\boldsymbol{x}_k, \boldsymbol{n}_k\right)}{\partial \boldsymbol{n}_k}\right|_{\boldsymbol{x}_{\mathrm{op}, \boldsymbol{k}}, \mathbf{0}} \end{aligned} yop,k=g(xop,k,0)Gk=∂xk∂g(xk,nk)xop,k,0Ck=∂nk∂g(xk,nk)xop,k,0按照与之前同样的方式进行推导,可得到滤波的校正过程为:
Kk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1x^k=xˇk+Kk(yk−yop,k−Gk(xˇk−xop,k))\begin{aligned} & \boldsymbol{K}_k=\check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}\left(\boldsymbol{G}_k \check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}+\boldsymbol{C}_k \boldsymbol{R}_k \boldsymbol{C}_k^{\mathrm{T}}\right)^{-1} \\ & \hat{\boldsymbol{x}}_k=\check{\boldsymbol{x}}_k+\boldsymbol{K}_k\left(\boldsymbol{y}_k-\boldsymbol{y}_{\mathrm{op}, k}-\boldsymbol{G}_k\left(\check{\boldsymbol{x}}_k-\boldsymbol{x}_{\mathrm{op}, k}\right)\right) \end{aligned} Kk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1x^k=xˇk+Kk(yk−yop,k−Gk(xˇk−xop,k))可见唯一的区别是后验均值 x^k\hat{\boldsymbol{x}}_kx^k 更新的公式与之前有所不同。
滤波过程中,反复执行这 2 个公式,以上次的后验均值作为本次的线性化工作点,即可达到减小非线性误差的目的。
需要注意的是,在这种滤波模式下, 后验方差应放在最后一步进行。
P^k=(1−KkGk)Pˇk\hat{\boldsymbol{P}}_k=\left(\mathbf{1}-\boldsymbol{K}_k \boldsymbol{G}_k\right) \check{\boldsymbol{P}}_k P^k=(1−KkGk)Pˇk
4. 基于滤波器的融合
通过以上推导,滤波问题可以简单理解为“预测 + 观测 = 融合结果”。
结合实际点云地图中定位的例子,预测由IMU给出,观测即为激光雷达点云和地图匹配得到的姿态和位置。
融合流程用框图可以表示如下:

4.1 状态方程
状态方程 FFF 由误差方程得来,第8讲已经完成误差方程的推导:
δp˙=δvδv˙=−Rt[at−bat]×δθ+Rt(na−δba)δθ˙=−[ωt−bωt]×δθ+nω−δbωδb˙a=nba或 δb˙a=0δb˙ω=nbωδb˙ω=0令 δx=[δpδvδθδbaδbω],w=[nanωnbanbω]\begin{aligned} & \delta \dot{\boldsymbol{p}}=\delta \boldsymbol{v} \\ & \delta \dot{\boldsymbol{v}}=-\boldsymbol{R}_t\left[\boldsymbol{a}_t-\boldsymbol{b}_{a_t}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{R}_t\left(\boldsymbol{n}_a-\delta \boldsymbol{b}_a\right) \\ & \delta \dot{\boldsymbol{\theta}}=-\left[\boldsymbol{\omega}_t-\boldsymbol{b}_{\omega_t}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{n}_\omega-\delta \boldsymbol{b}_\omega \\ & \delta \dot{\boldsymbol{b}}_a=\boldsymbol{n}_{b_a} \quad \text { 或 } \quad \delta \dot{\boldsymbol{b}}_a=0 \\ & \delta \dot{\boldsymbol{b}}_\omega=\boldsymbol{n}_{b_\omega} \quad\quad\quad { }^{ }{ }^{ }{ }^{ }{ }^{ }{ }^{ }{ }^{ } \delta \dot{\boldsymbol{b}}_\omega=0 \\ & \text { 令 } \delta \boldsymbol{x}=\left[\begin{array}{c} \delta \boldsymbol{p} \\ \delta \boldsymbol{v} \\ \delta \boldsymbol{\theta} \\ \delta \boldsymbol{b}_a \\ \delta \boldsymbol{b}_\omega \end{array}\right], \quad \boldsymbol{w}=\left[\begin{array}{l} \boldsymbol{n}_a \\ \boldsymbol{n}_\omega \\ \boldsymbol{n}_{b_a} \\ \boldsymbol{n}_{b_\omega} \end{array}\right] \end{aligned} δp˙=δvδv˙=−Rt[at−bat]×δθ+Rt(na−δba)δθ˙=−[ωt−bωt]×δθ+nω−δbωδb˙a=nba 或 δb˙a=0δb˙ω=nbωδb˙ω=0 令 δx=δpδvδθδbaδbω,w=nanωnbanbω则误差方程可以写成状态方程的通用形式:
δx˙=Ftδx+Btw\delta \dot{\boldsymbol{x}}=\boldsymbol{F}_t \delta \boldsymbol{x}+\boldsymbol{B}_t \boldsymbol{w} δx˙=Ftδx+Btw
其中:
Ft=[0I300000−Rt[a‾t]×−Rt000−[ω‾t]×0−I30000000000]a‾t=at−batω‾t=ωt−bωtBt=[0000Rt0000I30000I30000I3]\begin{aligned} \boldsymbol{F}_t & =\left[\begin{array}{ccccc} 0 & \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & -\boldsymbol{R}_t\left[\overline{\boldsymbol{a}}_t\right]_{\times} & -\boldsymbol{R}_t & \mathbf{0} \\ 0 & 0 & -\left[\overline{\boldsymbol{\omega}}_t\right]_{\times} & \mathbf{0} & -\boldsymbol{I}_3 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \begin{array}{c} \overline{\boldsymbol{a}}_t=\boldsymbol{a}_t-\boldsymbol{b}_{a_t} \\ \overline{\boldsymbol{\omega}}_t=\boldsymbol{\omega}_t-\boldsymbol{b}_{\omega_t} \end{array} \\ \boldsymbol{B}_t & =\left[\begin{array}{cccc} \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \boldsymbol{R}_t & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 \end{array}\right] \end{aligned} FtBt=00000I300000−Rt[at]×−[ωt]×000−Rt00000−I300at=at−batωt=ωt−bωt=0Rt00000I300000I300000I3注:当选择 δb˙a=0,δb˙ω=0\delta \dot{\boldsymbol{b}}_a=0 , \delta \dot{\boldsymbol{b}}_\omega=0δb˙a=0,δb˙ω=0 时,矩阵形式不一样,请各位自行推导。
4.2 观测方程
在滤波器中,观测方程 GGG 一般写为:
y=Gtδx+Ctn\boldsymbol{y}=\boldsymbol{G}_t \delta \boldsymbol{x}+\boldsymbol{C}_t \boldsymbol{n} y=Gtδx+Ctn此例中观测量有位置、失准角,则:
y=[δp‾δθ‾]\boldsymbol{y}=\left[\begin{array}{l} \delta \overline{\boldsymbol{p}} \\ \delta \overline{\boldsymbol{\theta}} \end{array}\right] y=[δpδθ]因此有:
Gt=[I3000000I300]Ct=[I300I3]\begin{aligned} \boldsymbol{G}_t & =\left[\begin{array}{ccccc} \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} \end{array}\right] \\ \boldsymbol{C}_t & =\left[\begin{array}{cc} \boldsymbol{I}_3 & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_3 \end{array}\right] \end{aligned} GtCt=[I30000I30000]=[I300I3]而此处 nnn 为观测噪声,
n=[nδpˉxnδpˉynδpˉznδθˉxnδθˉynδθˉz]T\boldsymbol{n}=\left[\begin{array}{llllll} n_{\delta \bar{p}_x} & n_{\delta \bar{p}_y} & n_{\delta \bar{p}_z} & n_{\delta \bar{\theta}_x} & n_{\delta \bar{\theta}_y} & n_{\delta \bar{\theta}_z} \end{array}\right]^T n=[nδpˉxnδpˉynδpˉznδθˉxnδθˉynδθˉz]T观测量中, δp\delta \boldsymbol{p}δp 的计算过程为:
δp‾=pˇ−p\delta \overline{\boldsymbol{p}}=\check{\boldsymbol{p}}-\boldsymbol{p} δp=pˇ−p其中 pˇ\check{\boldsymbol{p}}pˇ 为 IMU 解算的位置,即预测值。 p\boldsymbol{p}p 为雷达与地图 匹配得到的位置,即观测值。
δθ‾\delta \overline{\boldsymbol{\theta}}δθ 的计算过程稍微复杂,需要先计算误差矩阵,
δR‾t=RtTRˇt\delta \overline{\boldsymbol{R}}_t=\boldsymbol{R}_t^T \check{\boldsymbol{R}}_t δRt=RtTRˇt其中 Rˇt\check{\boldsymbol{R}}_tRˇt 为 IMU 解算的旋转矩阵,即预测值。Rt\boldsymbol{R}_tRt 为雷达与地图匹配得到的旋转矩阵,即观测值。
由于预测值与观测值之间的关系为:
Rˇt≈Rt(I+[δθ‾]×)\check{\boldsymbol{R}}_t \approx \boldsymbol{R}_t\left(\boldsymbol{I}+[\delta \overline{\boldsymbol{\theta}}]_{\times}\right) Rˇt≈Rt(I+[δθ]×)因此:
δθ‾=(δR‾t−I)∨\delta \overline{\boldsymbol{\theta}}=\left(\delta \overline{\boldsymbol{R}}_t-\boldsymbol{I}\right)^{\vee} δθ=(δRt−I)∨
4.3 构建滤波器
构建滤波器,即把融合系统的状态方程和观测方程应用到 Kalman 滤波的五个公式中。
前面推导的方程是连续时间的,要应用于离散时间,需要按照采样时间对其进行离散化。
状态方程离散化,可以写为:
δxk=Fk−1δxk−1+Bk−1wk\delta \boldsymbol{x}_k=\boldsymbol{F}_{k-1} \delta \boldsymbol{x}_{k-1}+\boldsymbol{B}_{k-1} \boldsymbol{w}_k δxk=Fk−1δxk−1+Bk−1wk其中:
Fk−1=I15+FtTBk−1=[0000Rk−1T0000I3T0000I3T0000I3T]\begin{aligned} \boldsymbol{F}_{k-1} & =\boldsymbol{I}_{15}+\boldsymbol{F}_t T \\ \boldsymbol{B}_{k-1}= & {\left[\begin{array}{cccc} \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \boldsymbol{R}_{k-1} T & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_3 T & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 \sqrt{T} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 \sqrt{T} \end{array}\right] } \end{aligned} Fk−1Bk−1==I15+FtT0Rk−1T00000I3T00000I3T00000I3T其中,TTT 为 Kalman 的滤波周期。
注:关于 Bk−1\boldsymbol{B}_{k-1}Bk−1 的离散化形式,不同资料有差异,但对实际调试影响不大。
对于观测方程,不需要乘以滤波周期,可以直接写出
yk=Gkδxk+Cknk\boldsymbol{y}_k=\boldsymbol{G}_k \delta \boldsymbol{x}_k+\boldsymbol{C}_k \boldsymbol{n}_k yk=Gkδxk+Cknk将以上各变量,带入kalman滤波的五个方程,即可构建完整的滤波器更新流程。
δxˇk=Fk−1δx^k−1+Bk−1wkPˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1TKk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1P^k=(I−KkGk)Pˇkδx^k=δxˇk+Kk(yk−Gkδxˇk)\begin{aligned} & \delta \check{\boldsymbol{x}}_k=\boldsymbol{F}_{k-1} \delta \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k-1} \boldsymbol{w}_k \\ & \check{\boldsymbol{P}}_k=\boldsymbol{F}_{k-1} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k-1}^{\mathrm{T}}+\boldsymbol{B}_{k-1} \boldsymbol{Q}_k \boldsymbol{B}_{k-1}^T \\ & \boldsymbol{K}_k=\check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}\left(\boldsymbol{G}_k \check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}+\boldsymbol{C}_k \boldsymbol{R}_k \boldsymbol{C}_k^T\right)^{-1} \\ & \hat{\boldsymbol{P}}_k=\left(\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{G}_k\right) \check{\boldsymbol{P}}_k \\ & \delta \hat{\boldsymbol{x}}_k=\delta \check{\boldsymbol{x}}_k+\boldsymbol{K}_k\left(\boldsymbol{y}_k-\boldsymbol{G}_k \delta \check{\boldsymbol{x}}_k\right) \end{aligned} δxˇk=Fk−1δx^k−1+Bk−1wkPˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1TKk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1P^k=(I−KkGk)Pˇkδx^k=δxˇk+Kk(yk−Gkδxˇk)
4.4 Kalman 滤波实际使用流程
4.4.1 位姿初始化

在点云地图中实现初始定位,并给以下变量赋值,
p^0\hat{\boldsymbol{p}}_0p^0 :初始时刻位置
v^0\hat{\boldsymbol{v}}_0v^0 :初始时刻速度(可以从组合导航获得)
R^0\hat{\boldsymbol{R}}_0R^0 : 初始时刻姿态(也可用四元数,后面不再强调)
4.4.2 Kalman 初始化
 a. 状态量 δx^0=0\delta \hat{\boldsymbol{x}}_0=\mathbf{0}δx^0=0
a. 状态量 δx^0=0\delta \hat{\boldsymbol{x}}_0=\mathbf{0}δx^0=0
b. 方差
P^0=[PδpPδvPδθPδbaPδbω]\hat{\boldsymbol{P}}_0=\left[\begin{array}{ccccc} \boldsymbol{P}_{\delta p} & & & & \\ & \boldsymbol{P}_{\delta v} & & & \\ & & \boldsymbol{P}_{\delta \boldsymbol{\theta}} & & \\ & & & \boldsymbol{P}_{\delta b_a} & \\ & & & & \boldsymbol{P}_{\delta b_\omega} \end{array}\right] P^0=PδpPδvPδθPδbaPδbω初始方差理论上可设置为各变量噪声的平方,实际中一般故意设置大一些,这样可加快收敛速度。
c. 过程噪声与观测噪声
Q=[QaQωQbaQbω]R0=[RδpRδθ]\boldsymbol{Q}=\left[\begin{array}{cccc} \boldsymbol{Q}_a & & & \\ & \boldsymbol{Q}_\omega & & \\ & & \boldsymbol{Q}_{b_a} & \\ & & & \boldsymbol{Q}_{b_\omega} \end{array}\right] \quad \quad \boldsymbol{R}_0=\left[\begin{array}{ll} \boldsymbol{R}_{\delta p} & \\ & \boldsymbol{R}_{\delta \theta} \end{array}\right] Q=QaQωQbaQbωR0=[RδpRδθ]过程噪声与观测噪声一般在 kalman 迭代过程中保持不变。
4.4.3 惯性解算

按照之前讲解的惯性解算方法,进行位姿更新,该位姿属于先验位姿。
a. 姿态解算
Rˇk=R^k−1(I+sinϕϕ(ϕ×)+1−cosϕϕ2(ϕ×)2)\check{\boldsymbol{R}}_k=\hat{\boldsymbol{R}}_{k-1}\left(I+\frac{\sin \phi}{\phi}(\phi \times)+\frac{1-\cos \phi}{\phi^2}(\boldsymbol{\phi} \times)^2\right) Rˇk=R^k−1(I+ϕsinϕ(ϕ×)+ϕ21−cosϕ(ϕ×)2)其中
ϕ=ω‾k−1+ω‾k2(tk−tk−1)ω‾k=ωk−bωkω‾k−1=ωk−1−bωk−1\begin{aligned} & \boldsymbol{\phi}=\frac{\overline{\boldsymbol{\omega}}_{k-1}+\overline{\boldsymbol{\omega}}_k}{2}\left(t_k-t_{k-1}\right) \\ & \overline{\boldsymbol{\omega}}_k=\boldsymbol{\omega}_k-\boldsymbol{b}_{\omega_k} \\ & \overline{\boldsymbol{\omega}}_{k-1}=\boldsymbol{\omega}_{k-1}-\boldsymbol{b}_{\omega_{k-1}} \end{aligned} ϕ=2ωk−1+ωk(tk−tk−1)ωk=ωk−bωkωk−1=ωk−1−bωk−1按照之前讲解的惯性解算方法,进行位姿更新,该位姿属于先验位姿。
b. 速度解算
vˇk=v^k−1+(Rˇka‾k+R^k−1a‾k−12−g)(tk−tk−1)\check{\boldsymbol{v}}_k=\hat{\boldsymbol{v}}_{k-1}+\left(\frac{\check{\boldsymbol{R}}_k \overline{\boldsymbol{a}}_k+\hat{\boldsymbol{R}}_{k-1} \overline{\boldsymbol{a}}_{k-1}}{2}-\boldsymbol{g}\right)\left(t_k-t_{k-1}\right) vˇk=v^k−1+(2Rˇkak+R^k−1ak−1−g)(tk−tk−1)
其中
a‾k=ak−baka‾k−1=ak−1−bak−1\begin{aligned} & \overline{\boldsymbol{a}}_k=\boldsymbol{a}_k-\boldsymbol{b}_{a_k} \\ & \overline{\boldsymbol{a}}_{k-1}=\boldsymbol{a}_{k-1}-\boldsymbol{b}_{a_{k-1}} \end{aligned} ak=ak−bakak−1=ak−1−bak−1c. 位置解算
p^k=pˇk−1+vˇk+v^k−12(tk−tk−1)\hat{\boldsymbol{p}}_k=\check{\boldsymbol{p}}_{k-1}+\frac{\check{\boldsymbol{v}}_k+\hat{\boldsymbol{v}}_{k-1}}{2}\left(t_k-t_{k-1}\right) p^k=pˇk−1+2vˇk+v^k−1(tk−tk−1)
4.4.4 Kalman 预测更新

执行kalman五个步骤中的前两步,即
δxˇk=Fk−1δx^k−1+Bk−1wkPˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1T\begin{aligned} & \delta \check{\boldsymbol{x}}_k=\boldsymbol{F}_{k-1} \delta \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k-1} \boldsymbol{w}_k \\ & \check{\boldsymbol{P}}_k=\boldsymbol{F}_{k-1} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k-1}^{\mathrm{T}}+\boldsymbol{B}_{k-1} \boldsymbol{Q}_k \boldsymbol{B}_{k-1}^T \end{aligned} δxˇk=Fk−1δx^k−1+Bk−1wkPˇk=Fk−1P^k−1Fk−1T+Bk−1QkBk−1T当然,这需要先根据公式计算 Fk−1\boldsymbol{F}_{k-1}Fk−1 和 Bk−1\boldsymbol{B}_{k-1}Bk−1 。
4.4.5 无观测时后验更新

无观测时,不需要执行kalman剩下的三个步骤,后验等于先验,即
δx^k=δxˇkP^k=Pˇkx^k=xˇk\begin{aligned} & \delta \hat{\boldsymbol{x}}_k=\delta \check{\boldsymbol{x}}_k \\ & \hat{\boldsymbol{P}}_k=\check{\boldsymbol{P}}_k \\ & \hat{\boldsymbol{x}}_k=\check{\boldsymbol{x}}_k \end{aligned} δx^k=δxˇkP^k=Pˇkx^k=xˇk
4.4.6 有观测时的量测更新

执行kalman滤波后面的三个步骤,得到后验状态量。
Kk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1P^k=(I−KkGk)Pˇkδx^k=δxˇk+Kk(yk−Gkδxˇk)\begin{aligned} & \boldsymbol{K}_k=\check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}\left(\boldsymbol{G}_k \check{\boldsymbol{P}}_k \boldsymbol{G}_k^{\mathrm{T}}+\boldsymbol{C}_k \boldsymbol{R}_k \boldsymbol{C}_k^T\right)^{-1} \\ & \hat{\boldsymbol{P}}_k=\left(\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{G}_k\right) \check{\boldsymbol{P}}_k \\ & \delta \hat{\boldsymbol{x}}_k=\delta \check{\boldsymbol{x}}_k+\boldsymbol{K}_k\left(\boldsymbol{y}_k-\boldsymbol{G}_k \delta \check{\boldsymbol{x}}_k\right) \end{aligned} Kk=PˇkGkT(GkPˇkGkT+CkRkCkT)−1P^k=(I−KkGk)Pˇkδx^k=δxˇk+Kk(yk−Gkδxˇk)
4.4.7 有观测时计算后验位姿

根据后验状态量,更新后验位姿。
p^k=pˇk−δp^kv^k=vˇk−δv^kR^k=Rˇk(I−[δθ^k]×)b^ak=bˇak−δb^akb^ωk=bˇωk−δb^ωk\begin{aligned} & \hat{\boldsymbol{p}}_k=\check{\boldsymbol{p}}_k-\delta \hat{\boldsymbol{p}}_k \\ & \hat{\boldsymbol{v}}_k=\check{\boldsymbol{v}}_k-\delta \hat{\boldsymbol{v}}_k \\ & \hat{\boldsymbol{R}}_k=\check{\boldsymbol{R}}_k\left(\boldsymbol{I}-\left[\delta \hat{\boldsymbol{\theta}}_k\right]_{\times}\right) \\ & \hat{\boldsymbol{b}}_{a_k}=\check{\boldsymbol{b}}_{a_k}-\delta \hat{\boldsymbol{b}}_{a_k} \\ & \hat{\boldsymbol{b}}_{\omega_k}=\check{\boldsymbol{b}}_{\omega_k}-\delta \hat{\boldsymbol{b}}_{\omega_k} \end{aligned} p^k=pˇk−δp^kv^k=vˇk−δv^kR^k=Rˇk(I−[δθ^k]×)b^ak=bˇak−δb^akb^ωk=bˇωk−δb^ωk
4.4.8 有观测时状态量清零

状态量已经用来补偿,因此需要清零。
δx^k=0\delta \hat{\boldsymbol{x}}_k=\mathbf{0} δx^k=0后验方差保持不变。
4.4.9 输出位姿
把后验位姿输出给其他模块使用,即输出 p^k\hat{\boldsymbol{p}}_kp^k,v^k\hat{\boldsymbol{v}}_kv^k,R^k\hat{\boldsymbol{R}}_kR^k (或 q^k\hat{\boldsymbol{q}}_kq^k)。
相关文章:

多传感器融合定位十-基于滤波的融合方法Ⅰ其二
多传感器融合定位十-基于滤波的融合方法Ⅰ其二3. 滤波器基本原理3.1 状态估计模型3.2 贝叶斯滤波3.3 卡尔曼滤波(KF)推导3.4 扩展卡尔曼滤波(EKF)推导3.5 迭代扩展卡尔曼滤波(IEKF)推导4. 基于滤波器的融合4.1 状态方程4.2 观测方程4.3 构建滤波器4.4 Kalman 滤波实际使用流程4…...
Java集合面试题:HashMap源码分析
文章目录一、HashMap源码二、HashMap数据结构模型图三、HashMap中如何确定元素位置四、关于equals与hashCode函数的重写五、阅读源码基本属性参考文章:史上最详细的 JDK 1.8 HashMap 源码解析参考文章:Hash详解参考文章:hashCode源码分析参考…...
,真题含思路)
华为OD机试 - 数组合并(Python),真题含思路
数组合并 题目 现在有多组整数数组, 需要将他们合并成一个新的数组。 合并规则, 从每个数组里按顺序取出固定长度的内容合并到新的数组中, 取完的内容会删除掉, 如果该行不足固定长度或者已经为空, 则直接取出剩余部分的内容放到新的数组中, 继续下一行。 如样例 1, 获得长度…...
Vue2创建移动端项目
一、Vscode Vscode 下载安装以及常用的插件 1、Vscode 下载 下载地址:Vscode 中文语言插件 搜索 chinese 主题 Atom 主题 文件图标主题 搜索 icon 源代码管理插件GitLens 搜索 GitLens Live Server _本地服务器 搜索 Live Server Prettier - Code formatt…...
PorterDuffXfermode与圆角图片
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 圆角图片 在项目开发中,我们常用到这样的功能:显示圆角图片。 这个是咋做的呢?我们来瞅瞅其中一种实现方式 /*** param bitmap 原图* p…...

如何准备大学生电子设计竞赛
大学生电子设计竞赛难度中上,一般有好几个类型题目可以选择,参赛者可以根据自己团队的能力、优势去选择合适自己的题目,灵活自主空间较大。参赛的同学们可以在暑假好好学习相关内容,把往年的题目拿来练练手。这个比赛含金量还是有…...

【Java容器(jdk17)】ArrayList深入源码,就是这么简单
ArrayList深入源码一、ArrayList源码解析1. MIXIN 的混入2. 属性说明3. 构造方法4. 其他方法(核心)iterator 和 listIterator 方法add方法remove 方法sort方法其他二、ArrayList 为什么是线程不安全的?体现哪些方面呢?三、ArrayLi…...
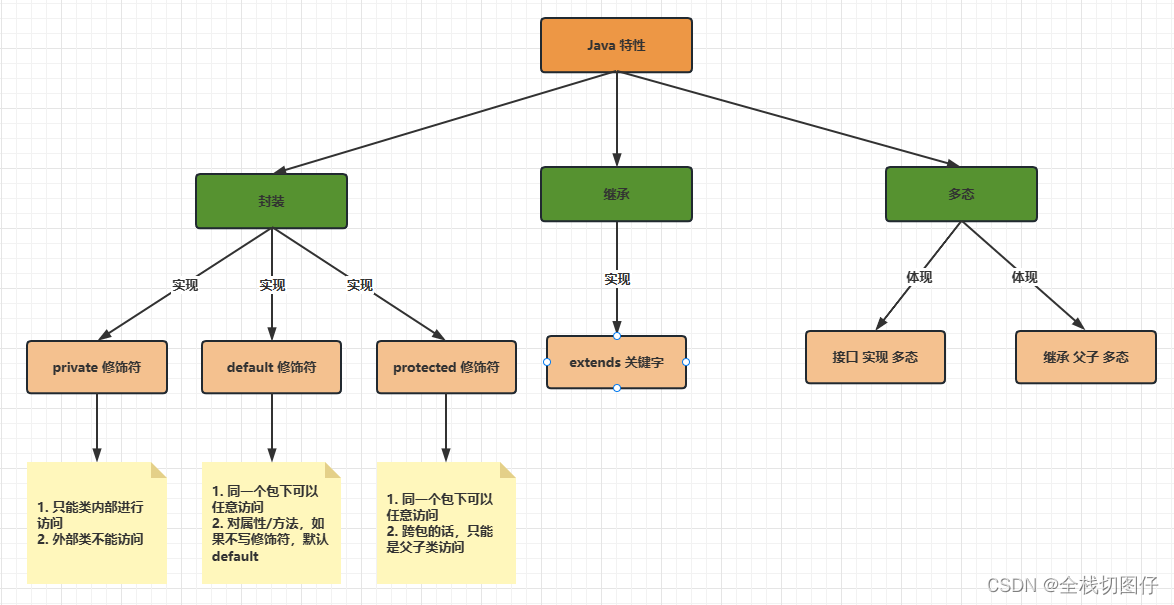
【Java 面试合集】简述下Java的三个特性 以及项目中的应用
简述下Java的特征 以及项目中的应用 1. 概述 上述截图中就是Java的三大特性,以及特性的实现方案。接下来就每个点展开来说说 2. 封装 满足:隐藏实现细节,公开使用方法 的都可以理解为是封装 而实现封装的有利手段就是权限修饰符了。可以根据…...
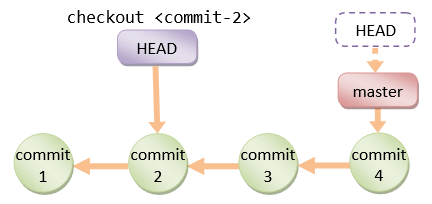
git基本概念图示【学习】
基本概念工作区(Working Directory)就是你在电脑里能看到的目录,比如名字为 gafish.github.com 的文件夹就是一个工作区本地版本库(Local Repository)工作区有一个隐藏目录 .git,这个不算工作区,…...

微前端qiankun架构 (基于vue2实现)使用教程
工具使用版本 node --> 16vue/cli --> 5 创建文件 创建文件夹qiankun-test。 使用vue脚手架创建主应用main和子应用dev 主应用 安装 qiankun: yarn add qiankun 或者 npm i qiankun -S 使用qiankun: 在 utils 内创建 微应用文件夹 microApp,在该文件夹…...

记录robosense RS-LIDAR-16使用过程3
一、wireshark抓包保存pcap文件并解析ubuntu18安装wireshark,参考下面csdn教程,官网教程我看的一脸蒙(可能英语太差)https://blog.csdn.net/weixin_46048542/article/details/121730448?spm1001.2101.3001.6650.2&utm_medium…...

【博学谷学习记录】大数据课程-学习第七周总结
Hadoop配置文件修改 Hadoop安装主要就是配置文件的修改,一般在主节点进行修改,完毕后scp下发给其他各个从节点机器 文件中设置的是Hadoop运行时需要的环境变量。JAVA_HOME是必须设置的,即使我们当前的系统中设置了JAVA_HOME,它也…...

154、【动态规划】leetcode ——494. 目标和:回溯法+动态规划(C++版本)
题目描述 原题链接:494. 目标和 解题思路 (1)回溯法 本题的特点是nums中每个元素只能使用一次,分别试探加上nums[index]和减去nums[index],然后递归的遍历下一个元素index 1。 class Solution { public:int res …...

MySQL-窗口函数
窗口函数概念常用窗口函数聚合窗口函数专用窗口函数语法OVER子句window_specwindow_name (命名窗口)partition_clause 分区order_clause 排序frame_clause 范围 (指定窗口大小)使用限制练习准备概念 窗口函数对一组查询执行类似于聚合的操作。然而&#…...

【C++设计模式】学习笔记(1):面向对象设计原则
目录 简介面向对象设计原则(1)依赖倒置原则(DIP)(2)开放封闭原则(OCP)(3)单一职责原则(SRP)(4)Liskov替换原则(LSP)(5)接口隔离原则(ISP)(6)优先使用对象组合,而不是类继承(7)封装变化点(8)针对接口编程,而不是针对实现编程结语简介 Hello! 非常感谢您阅读海…...

[测开篇]设计测试用例的方法如何正确描述Bug
文章目录为什么测试人员要写测试用例?怎样设计测试用例?(总的方面)1.基于需求设计测试用例(总的方面) 2.页面(总的方面) 3.非功能性测试(具体方面) 4.1 等…...

设计模式学习笔记--单例、建造者、适配器、装饰、外观、组合
以下内容根据以下网址及相关视频整理:Android设计模式之单例模式_谬谬清不给我取名字的博客-CSDN博客_android 单例模式 Android设计模式--单例模式的六种实现和单例模式讲解Volatile与Synchronized相关的并发_龙腾腾的博客-CSDN博客_android 单例 volatile java …...

English Learning - Day5 L1考前复习 2023.2.10 周五
English Learning - Day5 L1考前复习 2023.2.10 周五1 单选题:She has the face _________.2 单选题: The goals ________ he fought all his life no longer seemed important to him.3 单选题:Sales director is a position ______ communi…...

C. Prepend and Append
time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output Timur initially had a binary string†† s� (possibly of length 00). He performed the following operation several (possibly zero)…...
javassm超市在线配送管理系统
为了解决用户便捷地在网上购物,本文设计和开发了一个超市管理系统。本系统是基于web架构设计,SSM框架 ,使用Mysql数据库管理,综合采用JSP模式来完成系统的相关功能。主要实现了管理员与用户的注册与登陆,个人中心、用户…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
