【万题详解】P1048 [NOIP2005 普及组] 采药
题目描述
链接——题目在这里!!!
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有 2 个整数 T(1≤T≤1000)和 M(1≤M≤100),用一个空格隔开,T 代表总共能够用来采药的时间,M 代表山洞里的草药的数目。
接下来的 M 行每行包括两个在 1到 100 之间(包括 1 和 100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
输入输出样例
输入 #1
70 3
71 100
69 1
1 2
输出 #1
3
说明/提示
【数据范围】
-
对于 30% 的数据,M≤10;
-
对于全部的数据,M≤100。
【题目来源】
NOIP 2005 普及组第三题
解题思路
这几乎是一道和01背包例题一模一样的水题!!!
动态规划是一种强大的计算模式,其解决问题的方式是首先定义一组子问题,按照从小问题解决大问题的模式,依次解决所有子问题并最终求解原问题。 所以我们来回顾一下
步骤
第一步:确定子问题。 在这一步重点是分析那些变量是随着问题规模的变小而变小的, 那些变量与问题的规模无关。
第二步:确定状态:根据上面找到的子问题来给你分割的子问题限定状态
第三步:推到出状态转移方程:这里要注意你的状态转移方程是不是满足所有的条件, 注意不要遗漏。
第四步:确定边界条件:先根据题目的限制条件来确定题目中给出的边界条件是否能直接推导出, 如果不行也可以尝试从边界条件反推(举个例子:a(n)→a(2)有递推关系, 但是a(2)→a(1)不符合上述递推关系, 我们就可以考虑用a(1)来倒推出a(2), 然后将递推的终点设置为a(2));
第五步:确定实现方式:这个依照个人习惯 就像是01背包的两层for循环的顺序
第六步:确定优化方法:很多时候你会发现走到这里步的时候你需要返回第1步重来。首先考虑降维问题(优化内存), 优先队列、四边形不等式(优化时间)等等。
几个背包的模板
1.无优化
for(int i=1;i<=n;i++){ for(int j=1;j<=m1;j++){ if(j>=t[i]){f[i][j]=max(f[i-1][j-t[i]]+m[i],f[i-1][j]);}else{f[i][j]=f[i-1][j];}}
}
2.空间优化
for(int i=1;i<=n;i++){ for(int j=m;j>=0;j--){ //--是为了防止叠加 if(j>=w[i]){ f[j]=max(f[j],f[j-w[i]]+c[i]);} }
}
3.常数优化
for(int i=1;i<=n;i++){sum+=w[i];b=max(m-sum,w[i]);for(int j=m;j>=bound;j--){if(j>=w[i]){f[j]=max(f[j],f[j-w[i]]+c[i]);}}
}
4.完全背包
for(int i=1;i<=n;i++){ for(int j=0;j<=m;j++){ if(j>=w[i]){ f[j]=max(f[j],f[j-w[i]]+c[i]);} }}
回到正题
这道题吧,本蒟蒻认为用最简单的无优化版二维数组就可以,当然空间优化的也可以。
状态转移方程:
1.无优化版cpp f[i][j]=max(f[i-1][j-t[i]]+m[i],f[i-1][j]);
2.空间优化版
f[j]=max(f[j],f[j-w[i]]+c[i]);AC
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int f[N];
int main(){int n, m;cin >> n >> m;for(int i = 1; i <= m; i ++){int w, v;cin >> v >> w;for(int j = n; j >= v; j --){f[j] = max(f[j], f[j - v] + w);}}cout << f[n];return 0;
}结尾
希望大家多多关注!!!
如果你能支持一下我,我十分感谢!!!
如果有人想在洛谷上做题,可以点下方链接:
https://www.luogu.com.cn/
如果你喜欢或想了解一下其他的算法,可以看看以下这些:
洛谷指南
洛谷使用指南_洛谷怎么看-CSDN博客
题目详解系列(部分):
【万题详解】DFS搜索专题合集(上)-CSDN博客
【万题详解】P1314 [NOIP2011 提高组] 聪明的质监员-CSDN博客
【万题详解】洛谷P1282 多米诺骨牌-CSDN博客
【万题详解】洛谷P1238 走迷宫-CSDN博客
【万题详解】洛谷P1135奇怪的电梯-CSDN博客
【万题详解】洛谷P1510 精卫填海-CSDN博客
【万题详解】洛谷P1252 马拉松接力赛-CSDN博客
【万题详解】洛谷P1359 租用游艇-CSDN博客
【百题详解】洛谷P8508 做不完的作业-CSDN博客
【万题详解1】洛谷P1230 智力大冲浪-CSDN博客
【全网首发】洛谷贪心题解合集2-CSDN博客
【全网首发】洛谷贪心题解集合-CSDN博客
洛谷二分题集(3题)-CSDN博客
游戏系列:
C++棋类小游戏2-CSDN博客
C++自创棋类小游戏-CSDN博客
C++:史上最坑小游戏-CSDN博客
C++:自创小游戏-CSDN博客
C++:下雪-CSDN博客
C++讲解系列(算法):
C++:第十五讲高精度算法-CSDN博客
C++:第十四讲动态规划初步-CSDN博客
C++:第十三讲BFS广度优先搜索-CSDN博客
C++:第十二讲DFS深搜(二)_c++匿名函数dfs-CSDN博客
C++:第十一讲DFS深搜-CSDN博客
C++:第十讲二分查找-CSDN博客
前缀和与差分:
C++:第九讲前缀和与差分-CSDN博客
贪心:
C++:第八讲贪心算法1-CSDN博客
C++讲解系列(基础入门):
排序:
C++:第七讲冒泡排序-CSDN博客
函数:
C++第6讲max和min函数_c++ min函数-CSDN博客
C++第五讲函数初步-CSDN博客
for循环&数组:
C++第四讲for循环及数组-CSDN博客
if语句&else语句及运算:
C++第三讲:C++中的逻辑运算符及if else语句-CSDN博客
基础:
C++第二讲输入与输出-CSDN博客
C++第一讲认识C++编译器-CSDN博客
欢迎收看,希望大家能三连!
最后认识一下,我是爱编程的喷火龙廖,我们有缘再见!
相关文章:

【万题详解】P1048 [NOIP2005 普及组] 采药
题目描述 链接——题目在这里!!! 辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草…...
Golang基于Redis bitmap实现布隆过滤器(完结版)
Golang基于Redis bitmap实现布隆过滤器(完结版) 为了防止黑客恶意刷接口(请求压根不存在的数据),目前通常有以下几种做法: 限制IP(限流)Redis缓存不存在的key布隆过滤器挡在Redis前 …...

Java基础-内部类
内部类 引言内部类的共性成员内部类静态内部类非静态内部类 局部内部类匿名内部类内部类的使用场景和好处 引言 Java不仅可以定义变量和方法,还可以定义类. 内部类允许你把一些逻辑相关的类组织在一起,并可以控制内部中类的可见性. 这么看来,内部类就像是代码一种隐藏机制:将类…...
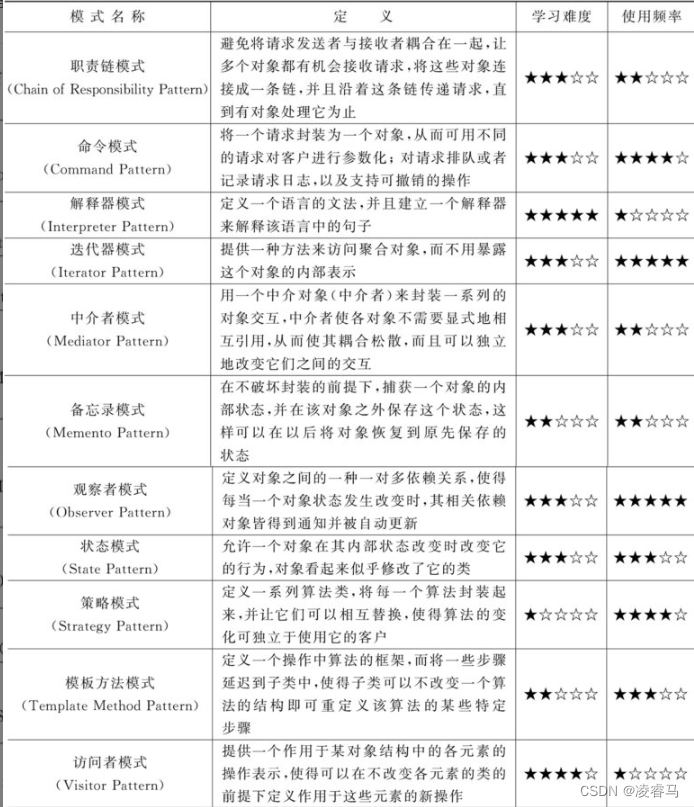
设计模式-行为型模式-职责链模式
在软件系统运行时,对象并不是孤立存在的,它们可以通过相互通信协作完成某些功能,一个对象在运行时也将影响到其他对象的运行。行为型模式(Behavioral Pattern)关注系统中对象之间的交互,研究系统在运行时对…...

代码随想录算法训练营第四十天|LeetCode343 整数拆分、LeetCode96 不同的二叉搜索树
343.整数拆分 思路:确定dp数组以及下标的含义 dp[i]代表 i可以被拆分后的最大乘积。确定递推公式,假如拆成连个数,dp[i] j*(i-j),拆成两个数以上,dp[i]j*dp[i-j],j的范围为1到i-1.dp[i]找到所有情况的最大值。初始化…...
接口自动化测试用例如何设计
说到自动化测试,或者说接口自动化测试,多数人的第一反应是该用什么工具,比如:Python Requests、Java HttpClient、Apifox、MeterSphere、自研的自动化平台等。大家似乎更关注的是哪个工具更优秀,甚至出现“ 做平台的 &…...

弱电综合布线:连接现代生活的纽带
在当今信息化快速发展的时代,弱电网络布线作为信息传输的重要基础设施,其作用日益凸显。它不仅保障了数据的高效流通,还确保了通信的稳定性。从商业大厦到教育机构,从政府机关到医院急救中心,再到我们居住的社区&#…...
Java零基础 - 数组的定义和声明
哈喽,各位小伙伴们,你们好呀,我是喵手。 今天我要给大家分享一些自己日常学习到的一些知识点,并以文字的形式跟大家一起交流,互相学习,一个人虽可以走的更快,但一群人可以走的更远。 我是一名后…...

CSS补充(下),弹性布局(上)
高级选择器 1.兄弟选择器 2.同时满足 div.bg{background-color: red;}p.bg{background-color: green;}spam.bg{background-color: blue;}注:选择器中间没有空格,有明确标识的选择器写在后面 3.各种伪类的应用 3.1作为第几个子元素 选择器:nth-child…...
)
图数据库 之 Neo4j - 应用场景4 - 反洗钱(9)
原理 Neo4j图数据库可以用于构建和分析数据之间的关系。它使用节点和关系来表示数据,并提供实时查询能力。通过使用Neo4j,可以将大量的交易数据导入图数据库,并通过查询和分析图结构来发现洗钱行为中的模式和关联。 案例分析 假设有一家转账服务公司,有以下交易数据,每个…...

uboot分区介绍
RK平台的U-Boot支持两种分区表 RK paramter格式(旧)和 标准GPT格式(新),当机器上同时存在 两种分区表时,优先使用GPT分区表。无论是 GPT 还是 RK parameter,烧写用的分区表文件都叫parameter.t…...

快速收集诊断信息,敏捷诊断工具obdiag应用实践——《OceanBase诊断系列》之三
1. 前言 作为OceanBase的敏捷诊断工具,obdiag具有以下特点: 部署便捷:提供rpm包和OBD上部署的模式,都能够一键部署安装。用户可以选择将其部署到集群中任意一台能连接到各个节点的设备上,而不仅限于OBServer节点。即…...
C++错误总结(1)
1.定义函数类型时,如果没有返回值,用void void swap(int &x, int &y){ int tem x; x y; y tem; } 2.输入时,不加换行符 cin >> a >> b >> c >> endl ;(红色标记的是错误的部分) 3.【逆序出入…...

std::shared_from_this注意事项:exception bad_weak_ptr
1.不可以在构造函数中调用shared_from_this() 因为它的实现是: _LIBCPP_INLINE_VISIBILITYshared_ptr<_Tp> shared_from_this(){return shared_ptr<_Tp>(__weak_this_);}也就是它依赖的__weak_this_此时还未创建完成。 2.一定要public继承 class MyTy…...
【工具】Raycast – Mac提效工具
引入 以前看到同事们锁屏的时候,不知按了什么键,直接调出这个框,然后输入lock屏幕就锁了。 跟我习惯的按Mac开机键不大一样。个人觉得还是蛮炫酷的~ 调研 但是由于之前比较繁忙,这件事其实都忘的差不多了࿰…...

蓝桥杯集训·每日一题2024 (二分,双指针)
前言: 开学了,平时学习的压力也逐渐大起来了,不过还算可以接受,等到后面阶段考的时候就不一样了,我目前为了转专业退选了很多课,这些课我都需要花时间来刷绩点,不然保研就没有竞争力了。我自己会…...
在Linux(Ubuntu)中使用终端编译 vscode安装
文章目录 📚在Linux(Ubuntu)中使用终端编译🐇.cpp程序编译🐇.py程序编译🐇查看Python、C编程环境 📚vscode安装 📚在Linux(Ubuntu)中使用终端编译 虚拟机安装…...
官网正在被哪些产品蚕食,定制网站又被哪些建站产品挤占。
2023-12-09 16:22贝格前端工场 官网建设是一个被大多数人看衰的市场,本文来理性分析下,谁在蚕食这个市场,谁又在挤占这个产品生存空间,欢迎大家评论,探讨。 网站正在被以下产品形式取代: 1. 移动应用&…...
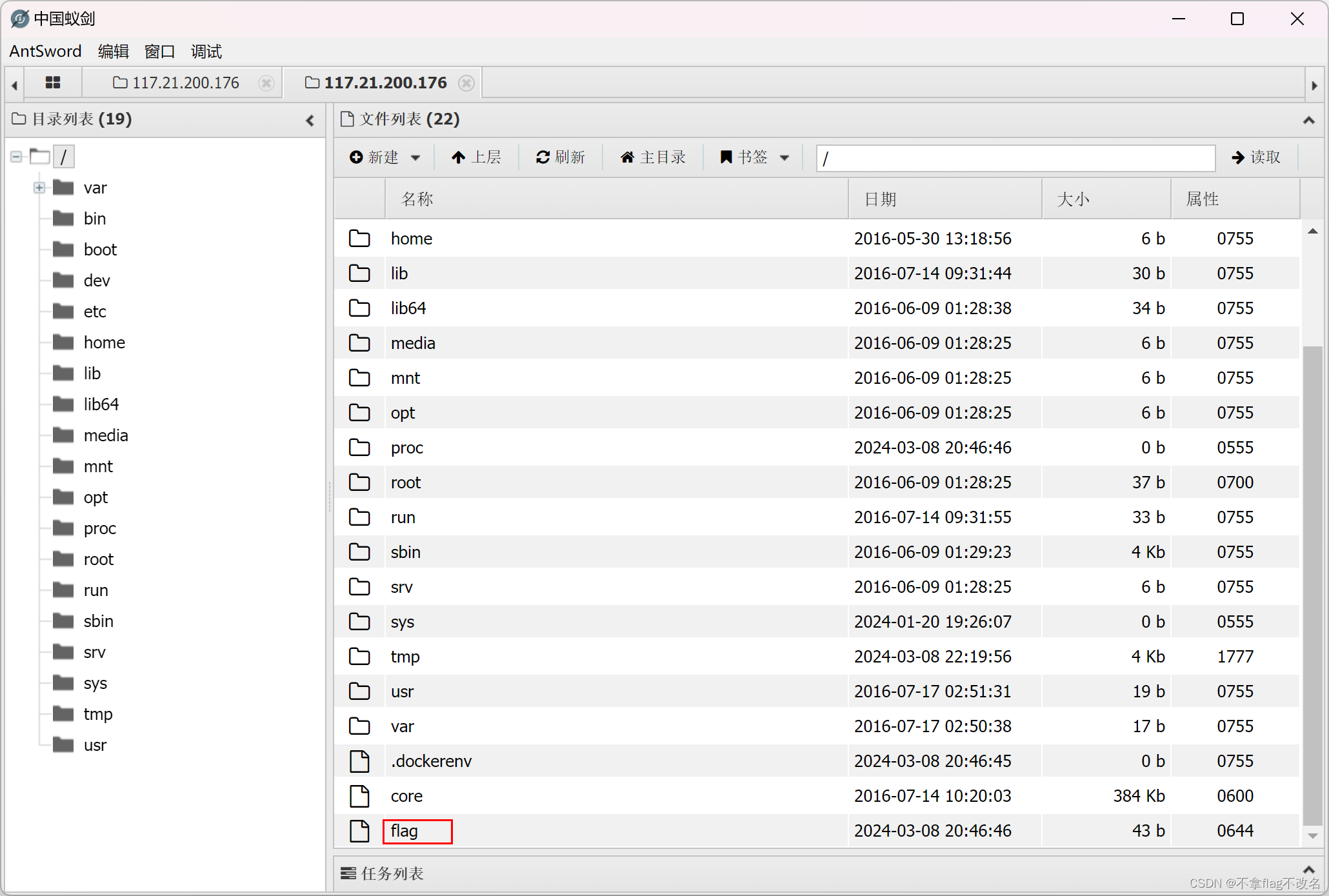
BUUCTF---[MRCTF2020]你传你呢1
1.题目描述 2.打开题目链接 3.上传shell.jpg文件,显示连接成功,但是用蚁剑连接却连接不上。shell文件内容为 <script languagephp>eval($_REQUEST[cmd]);</script>4.用bp抓包,修改属性 5.需要上传一个.htaccess的文件来把jpg后缀…...
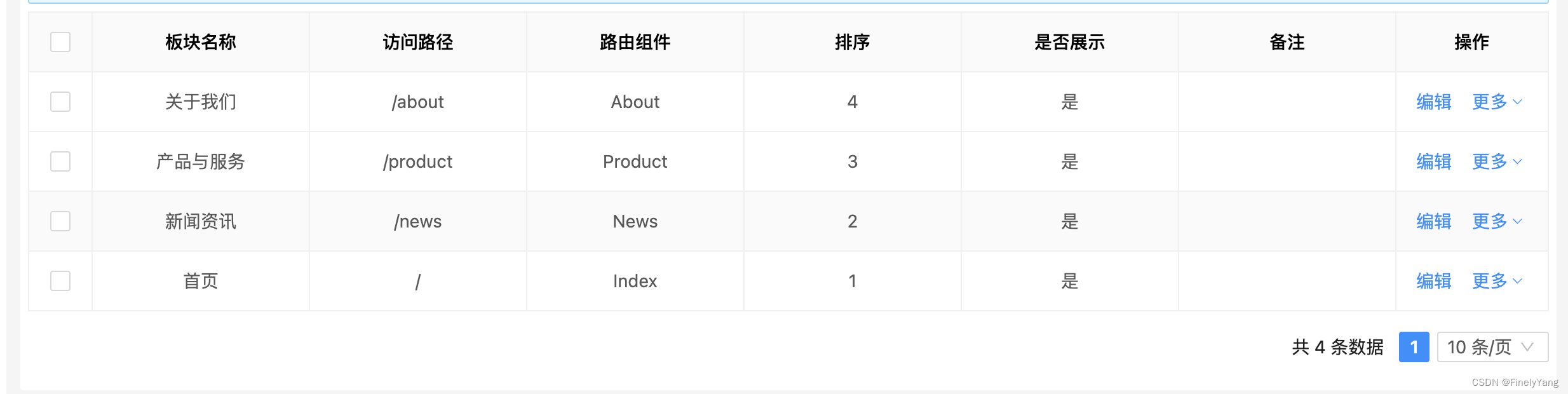
vite+vue3门户网站菜单栏动态路由控制
门户网站用户端需要分板块展示,板块内容由管理端配置,包括板块名称,访问路径,路由组件,展示顺序,是否展示。如下图所示: 用户访问门户网站时,展示菜单跳转通过板块配置,动…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
