神经网络的矢量化,训练与激活函数
我们现在再回到我们的神经元部分,来看我们如何用python进行正向传递。
单层的正向传递:
我们回到我们的线性回归的函数。我们每个神经元通过上述的方法,就可以得到我们的激发值,从而可以继续进行下一层。

我们用这个方法就可以得到我们的激发值,以及输出值。
我们用更加简便的python编码。
 我们先把我们需要用到的特征值w,b写成矩阵。
我们先把我们需要用到的特征值w,b写成矩阵。
def dense(a_in, W, b, g):units = W.shape[1]a_out = np.zeros(units)for j in range(units):w = W[:, j]z = np.dot(w, a_in) + b[j]a_out[j] = g(z)return a_out我们在下面继续每一层,正向传递。
def sequential (x):a1 = dense(x, W, b )a2 = dense(a1, W, b )a3 = dense(a2, W, b )a4 = dense(a3, W, b )f_x = a4return f_x这样子我们就可以进行一个完整的神经网络。
Ai中的ANI和AGI
实际上,我们的AI分为两个部分,第一部分叫做ANI,也就是人工狭义智能,它也就是现在我们很多人在研究的部分,而AGI被称为是人工智能,它是更加贴近于我们人的AI。
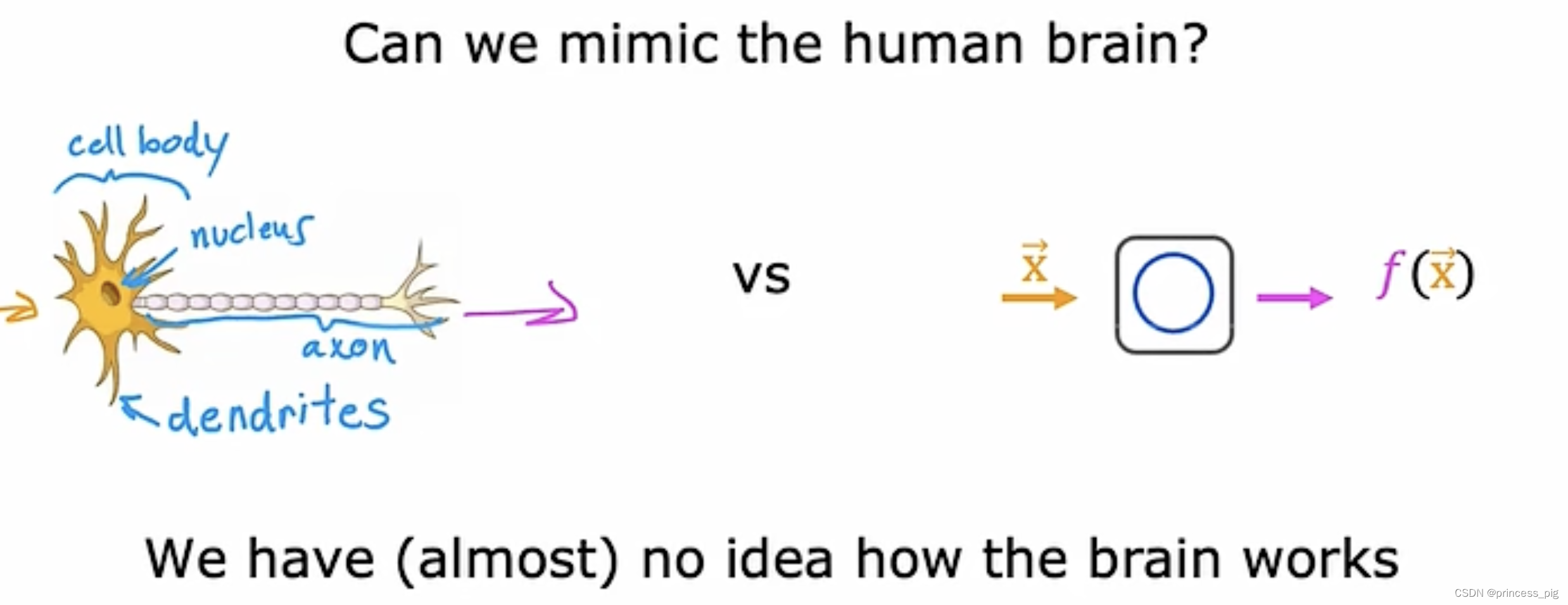
但是我们对于人脑的研究也并不完全,导致我们做出的根据神经元做出的结构也远不能达到人工智能的标准。
神经网络的矢量化实现:
在神经网络的矢量化,可以让我们的正向传统更加的简便。与我们之前的用循环的方式不同的是,
W = np.array([[1, -3, 5],[2, -4, 6]])b = np.array([[1, 1, 2]])
a_in = np.array([[2, -4]])def dense(a_in, W, b, g):units = W.shape[1]a_out = np.zeros(units)for j in range(units):w = W[:, j]z = np.dot(w, a_in) + b[j]a_out[j] = g(z)return a_out上述的是之前我们使用循环写成的一个神经层的输入与输出。
W = np.array([[1, -3, 5],[2, -4, 6]])b = np.array([[1, 1, 2]])
a_in = np.array([[2, -4]])def dense(a_in, W, b, g):#通过我们的矩阵乘法,我们可以得到我们需要的矩阵Z = np.matmul(a_in,W) + b#使用我们的激发函数,得到我们的输出,也是一个矩阵A_out = g(Z)#返回我们的矩阵return A_out
[[1,-1]]我们把我们在循环的方法换成了我们的矢量相乘的方法,这个方法很好的帮我们的代码得到了大量的简便。
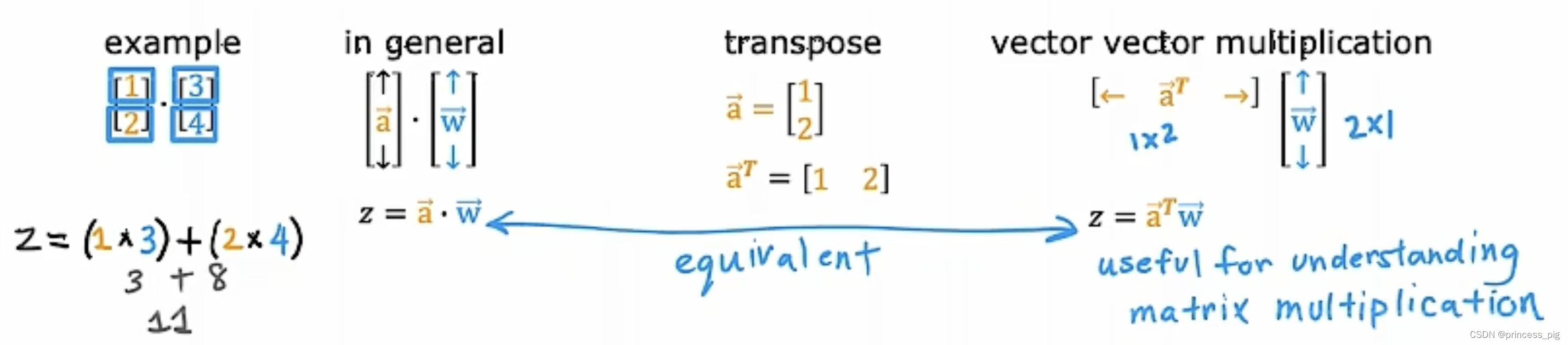
向量的基本性质:
这部分不做过多的解释。


用程序写矩阵乘法:
A = np.array([[1,-1,-0.1],[2,-2,-0.2]])
AT = np.array([[1,2],[-1,-2],[-0.1,-0.2]])
#用T来进行转制
AT = A.TW = np.array([[3,5,7,9],[2,4,8,0]])
#矩阵乘法
Z = np.matmul(AT,W)
#也可以用@
z = AT @ W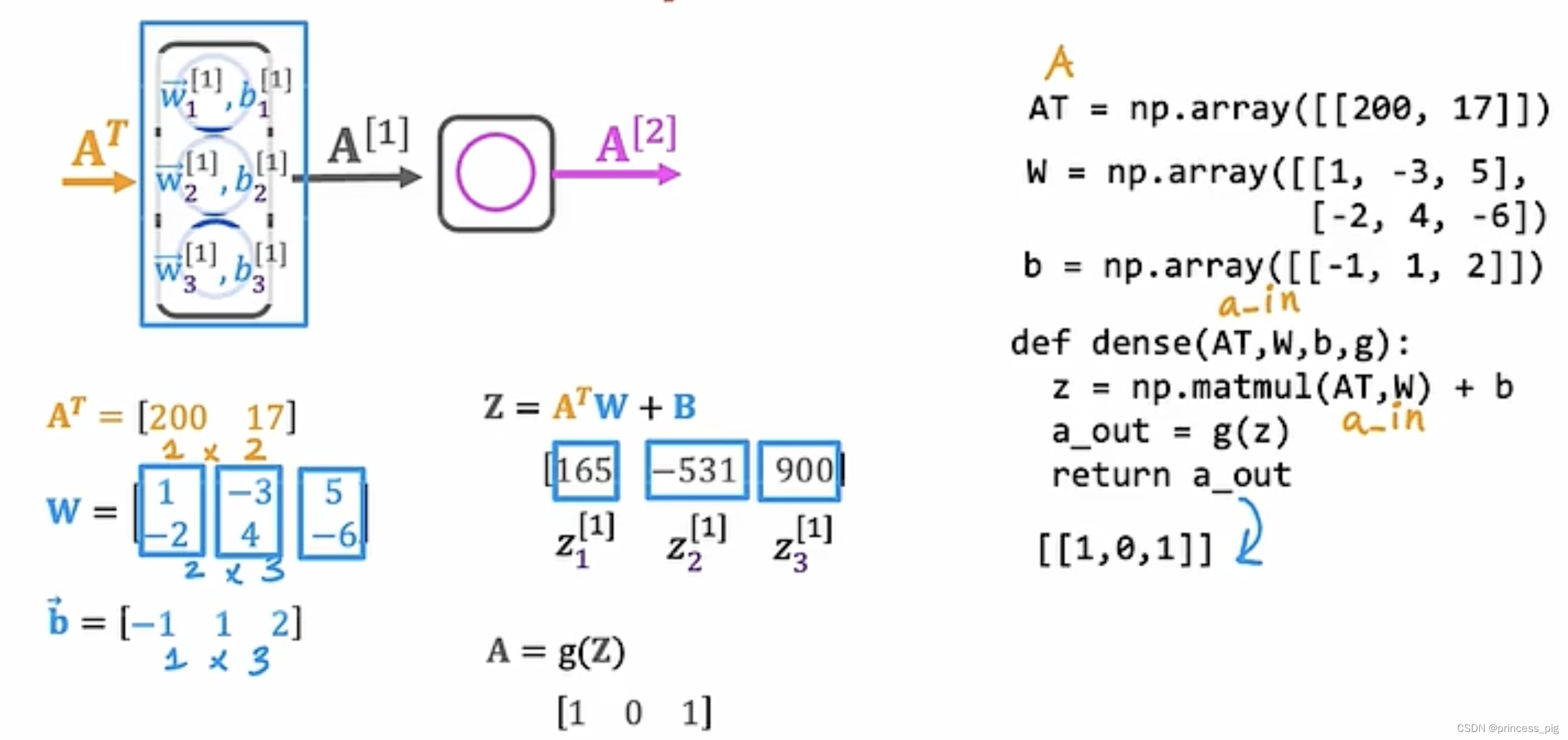 训练神经网络:
训练神经网络:
我们在训练神经网络中,主要有三步骤:
1.计算推理,2. 利用特定的损失函数编译模型,3.训练模型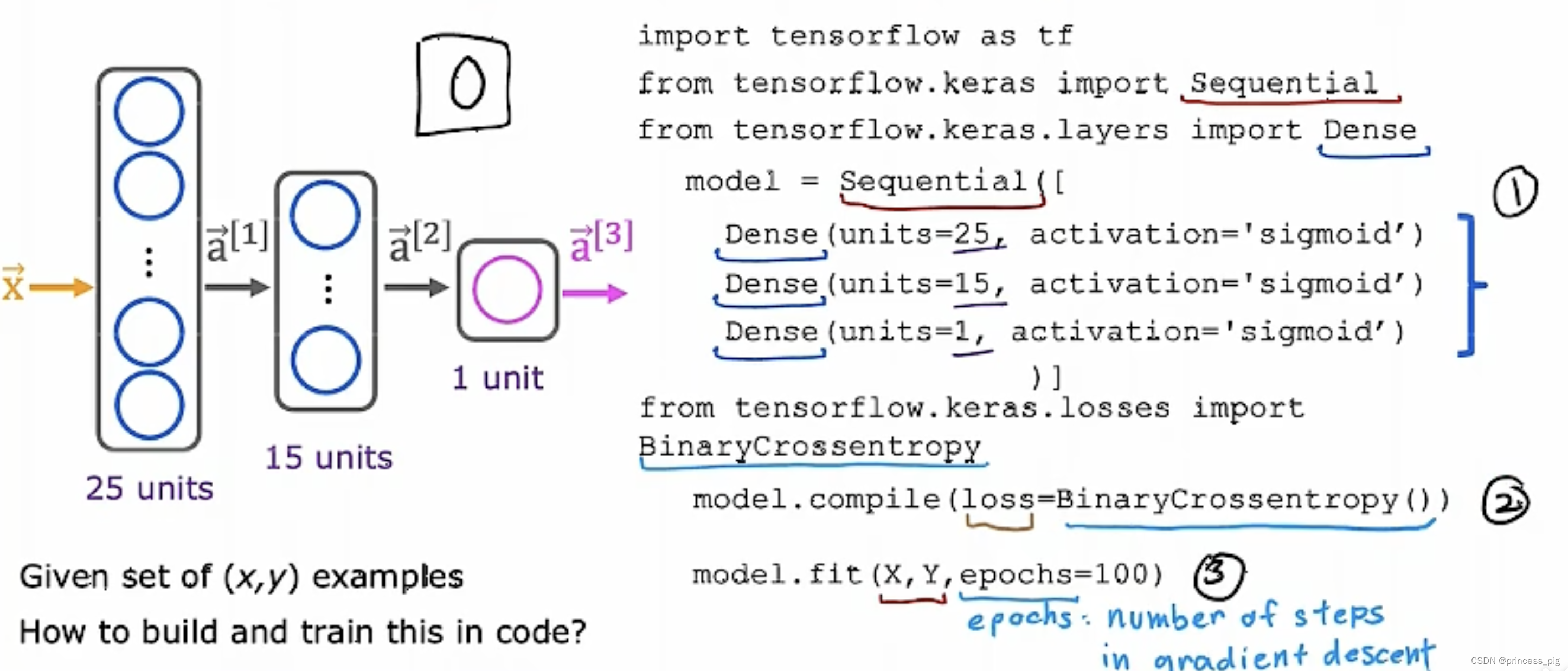

接下来,我们从逻辑回归的 角度去寻找我们如何在tensor flow来训练我们的神经网络。
第一步创建模型:
import tensorflow as tf
import numpy as np
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Densemodel = Sequential([Dense(units=25, activation="sigmoid"),Dense(units=15, activation="sigmoid"),Dense(units=1, activation="sigmoid")
])
第二步指定损失函数:
我们在这里用到一个函数叫做:BinaryCrossentropy(),它作为我们的逻辑函数的损失函数。
from tensorflow.keras.losses import BinaryCrossentropy
model.compile(loss=BinaryCrossentropy())当然,这个是用于我们的逻辑回归的,当我们只需要解决回归问题时,我们用到的是MeanSquaredError()这个方法。
from tensorflow.keras.losses import MeanSquaredError
model.compile(loss=MeanSquaredError())
第三步梯度下降,最小化成本函数:
在这里我们为了去训练我们的数据,我们用到的是逆向传递的算法。也就是我们的fit()函数 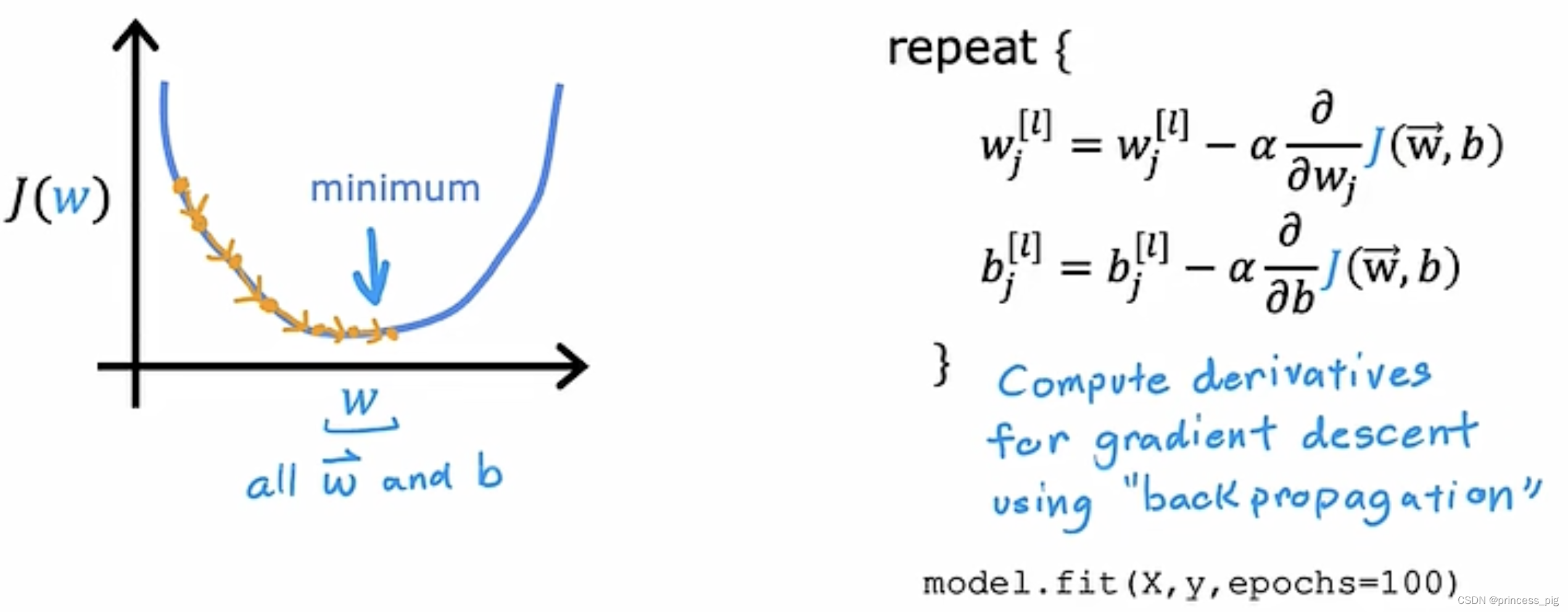
model.fit(X,y,epochs=100)epochs指的是进行100训练。
不同的激活函数:
我们在这里介绍了一个RELU的激活函数:简单来说它就是我们的取0和Z中的最大值 。
还有一个是我们的,它似乎和加上这个激活函数的效果没有任何变化,所以它也被我们叫做线性激活函数。
上图三个激活函数,是我们使用的比较多的。
选择激活函数:
选择我们对应的激活函数,我们主要观察的就是我们的所要求得的值的范围。
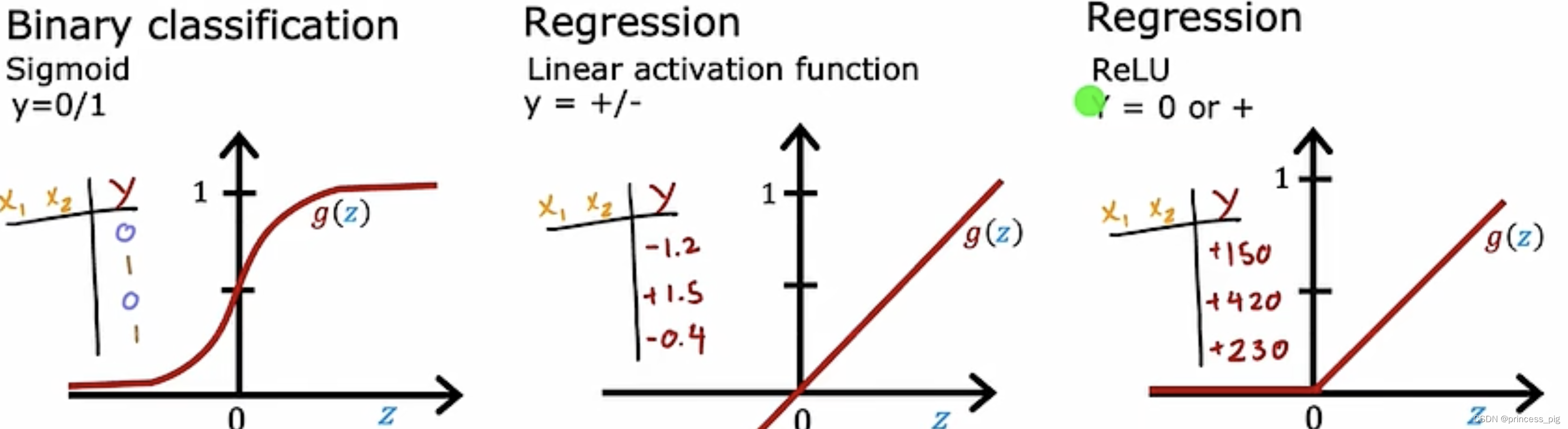
比如:我们用到了我们的sigmoid函数 ,就用在我们需要得到1或着0时,而我们的线性激活函数,则用在我们输出无论正负的范围,而我们的ReLu函数,则是对于大于0的部分。
在我们使用我们的激活函数时,函数的平坦度会影响我们梯度下降的速度,会导致我们的成本函数取到最小值的时间变长,但我们用ReLu函数则在代码运行时,更加的快。
所以,最好的方式就是在隐藏层,我们更多是使用我们的ReLu函数,因为它的下降更加的快,对于我们函数的运行有好处,而在最后输出层,我们则可以根据我们的需要选择我们的激活函数。
Dense(units=25, activation="linear"),
Dense(units=15, activation="relu"),
Dense(units=1, activation="sigmoid")这是三个不同的激活函数的写法。
为什么我们一定要用到激活函数呢?
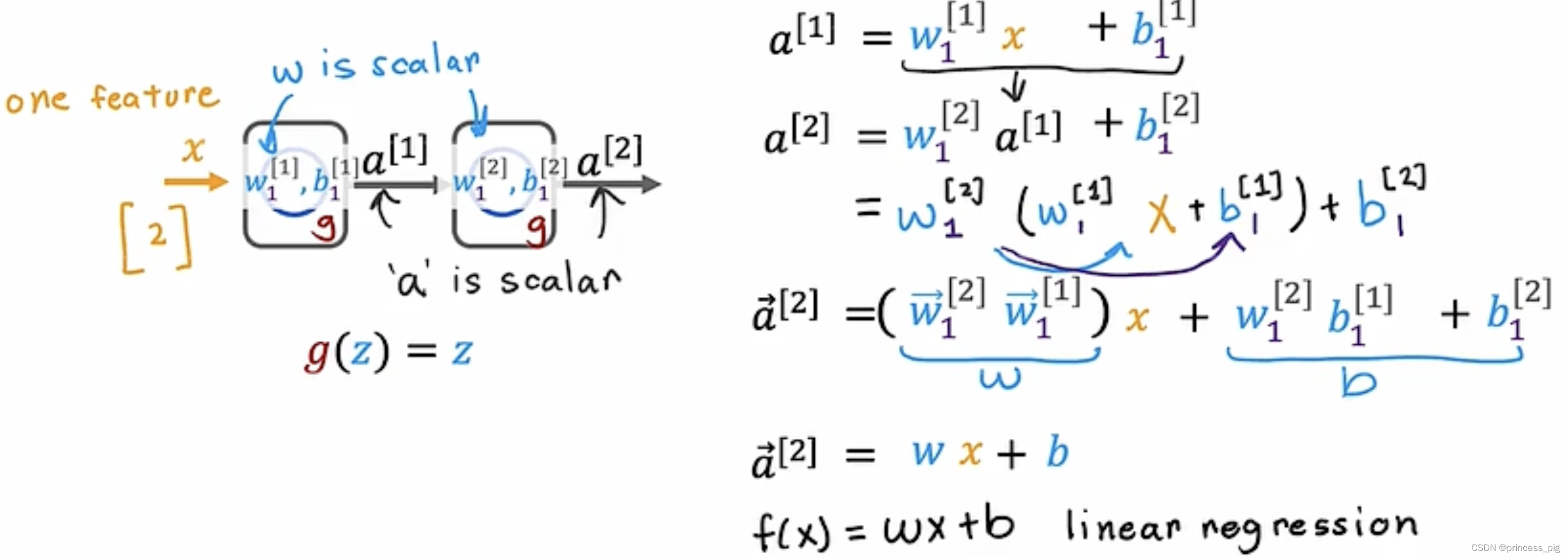
看一下,以下的推导,我们会发现无论是多少层的隐藏层和输出层,经过化简之后,我们得到的依旧是一个线性回归的式子,这样我们就可以只使用我们的线性回归就可以完成这个模型。所以在这里有一个共识就是不要在我们的隐藏层里使用我们的线性激活函数。
相关文章:

神经网络的矢量化,训练与激活函数
我们现在再回到我们的神经元部分,来看我们如何用python进行正向传递。 单层的正向传递: 我们回到我们的线性回归的函数。我们每个神经元通过上述的方法,就可以得到我们的激发值,从而可以继续进行下一层。 我们用这个方法就可以得…...
3.7号freeRtoS
1. 串口通信 配置串口为异步通信 设置波特率,数据位,校验位,停止位,数据的方向 同步通信 在同步通信中,数据的传输是在发送端和接收端之间通过一个共享的时钟信号进行同步的。这意味着发送端和接收端的时钟需要保持…...

瑞芯微 | I2S-音频基础 -1
最近调试音频驱动,顺便整理学习了一下i2s、alsa相关知识,整理成了几篇文章,后续会陆续更新。 喜欢嵌入式、Li怒晓得老铁可以关注一口君账号。 1. 音频常用术语 名称含义ADC(Analog to Digit Conversion)模拟信号转换…...
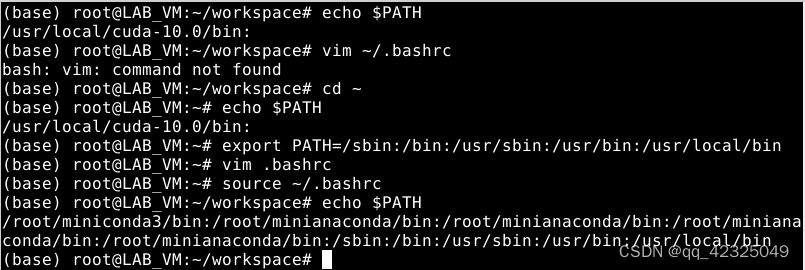
Linux配置.bashrc文件导致各种命令(vim、sudo)失效。
Linux配置.bashrc文件导致各种命令(vim、sudo)失效。 起因是 nvcc-V一直报错:-bash:nvcc: command not found 踩坑记录:上网一查说是没有配置cuda的环境变量。于是去修改了bashrc文件,在最下面…...

Visual Studio 2022 Version 17.9 新功能
Visual Studio 2022 v17.9 为广大 C 开发者引入了一系列好用的新功能和改进优化。 内存布局 现在,你可以使用【内存布局,Memory Layout】功能以可视化的方式来查看对象,结构体及联合体的内存布局信息,这可比以前需要手动查看内存…...

ArrayList 和 LinkedList 的区别
ArrayList ArrayList 是基于动态数组实现的, 它使用一块连续的内存空间来存储元素,因此访问元素的速度非常快(时间复杂度为 O(1)), 但是,在插入或删除元素时,如果位置不在数组末尾࿰…...

VGG16-CF-VGG11实验报告
说明:VGG16和CF-VGG11是论文《A 3D Fluorescence Classification and Component Prediction Method Based on VGG Convolutional Neural Network and PARAFAC Analysis Method》使用的两种主要模型。其对应代码仓库提供了实验使用的数据集、平行因子分析结果和CNN模型。论文和…...
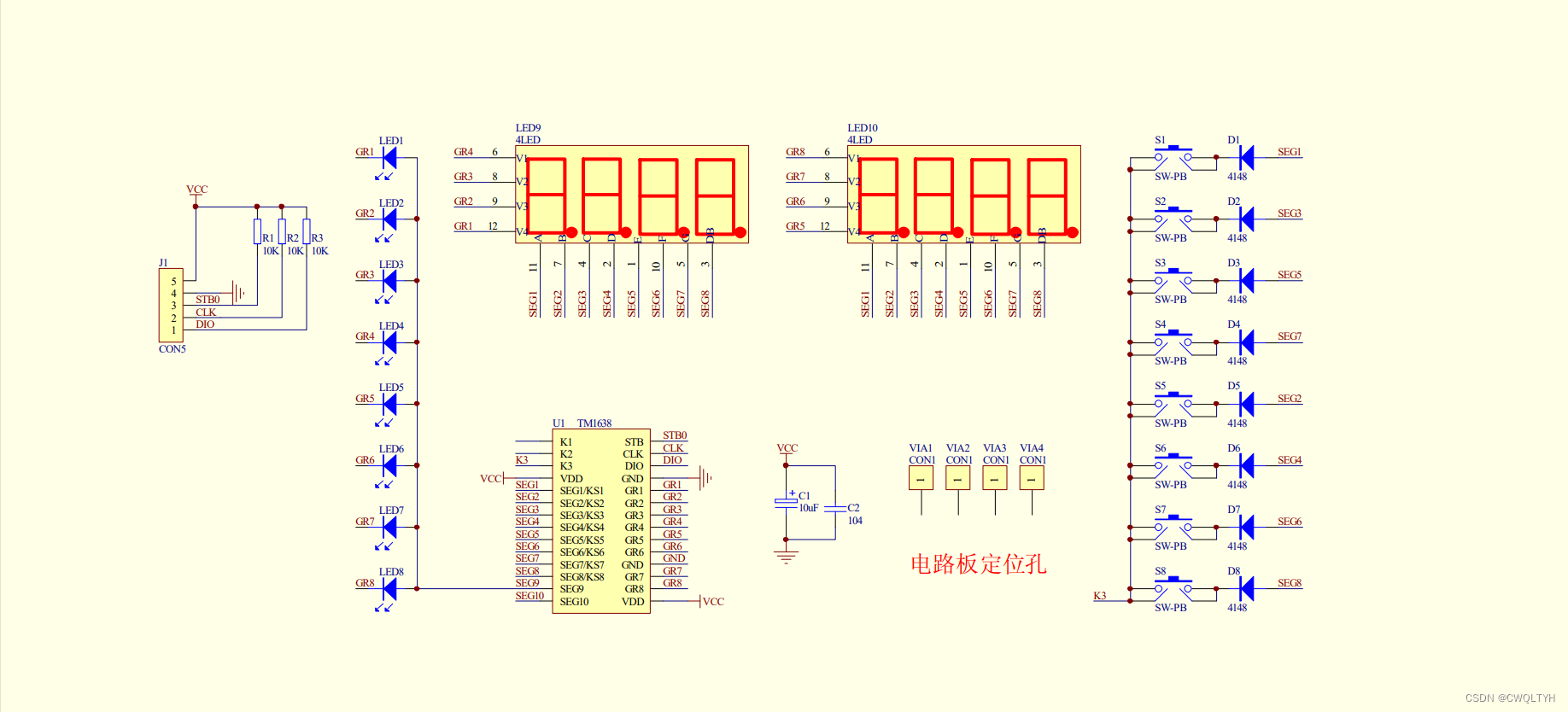
基于STC12C5A60S2系列1T 8051单片机的TM1638键盘数码管模块的按键扫描、数码管显示按键值、显示按键LED应用
基于STC12C5A60S2系列1T 8051单片机的TM1638键盘数码管模块的按键扫描、数码管显示按键值、显示按键LED应用 STC12C5A60S2系列1T 8051单片机管脚图STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式及配置STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式介绍TM1638键盘…...
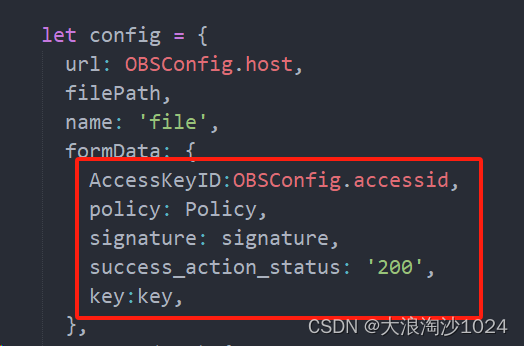
uniapp使用华为云OBS进行上传
前言:无论是使用华为云还是阿里云,使用其产品的时候必须阅读文档 1、以华为云为例,刚接触此功能肯定是无从下手的情况,那么我们需要思考,我们使用该产品所用到的文档是什么 2、我们要使用obs 文件上传,肯…...

用一个 Python 脚本实现依次运行其他多个带 argparse 命令行参数的 .py 文件
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 问题描述:在 Windows 环境中,您希望通过一个 Python 脚本来实现特定的自动化任务,该任务需要依次运行其他多个带 argparse 命令行参数的 .py 文件。您希望找到一种简…...

力扣热题100_普通数组_189_轮转数组
文章目录 题目链接解题思路解题代码 题目链接 189. 轮转数组 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] …...

讲解linux下的Qt如何编译oracle的驱动库libqsqloci.so
1.需求 最近linux下的Qt项目中要连接oracle数据库,用户需要我们访问他们的oracle数据库,查询数据 2.遇到的问题 qt连接oracle数据库需要oracle的驱动库libqsqloci.so插件,需要编译下,之前没有编译过,看了网上的…...

SpringCloud Ribbon 负载均衡服务调用
一、前言 接下来是开展一系列的 SpringCloud 的学习之旅,从传统的模块之间调用,一步步的升级为 SpringCloud 模块之间的调用,此篇文章为第三篇,即介绍 Ribbon 负载均衡服务调用 二、概述 2.1 Ribbon 是什么 Spring Cloud Ribbon…...

物联网在智慧城市建设中的关键作用:连接、感知、智能响应
一、引言 随着信息技术的飞速发展,物联网(IoT)技术已经渗透到我们生活的方方面面,特别是在智慧城市建设中发挥着至关重要的作用。智慧城市是指通过运用先进的信息和通信技术,实现城市基础设施、公共服务、交通管理、环…...
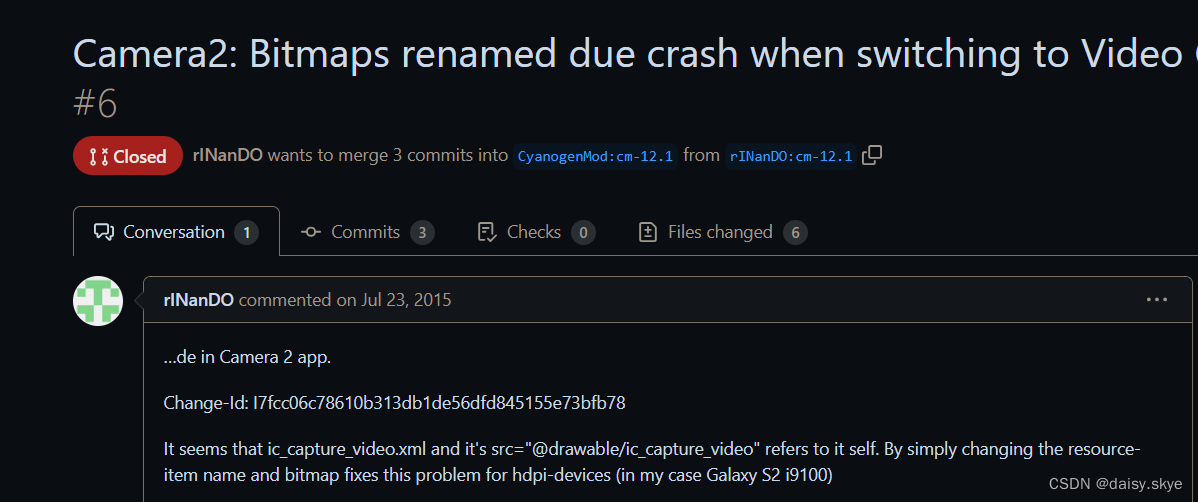
安卓7原生相机切到视频崩溃
目录 1、查看日志 2、分析日志、提取重点 3、寻找解决方法 author daisy.skye的博客_CSDN博客-嵌入式,Qt,Linux领域博主 daisy.skye_嵌入式,Linux,Qt-CSDN博客daisy.skye擅长嵌入式,Linux,Qt,等方面的知识https://blog.csdn.net/qq_40715266?typeblog 1、查看日志 由于安…...

构建信息蓝图:概念模型与E-R图的技术解析
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua,在这里我会分享我的知识和经验。&#x…...

docker拉取镜像失败的解决方案大全
更换国内源 创建或修改 /etc/docker/daemon.json 文件,修改: {"registry-mirrors" : ["https://registry.docker-cn.com","http://hub-mirror.c.163.com","https://docker.mirrors.ustc.edu.cn","https:…...
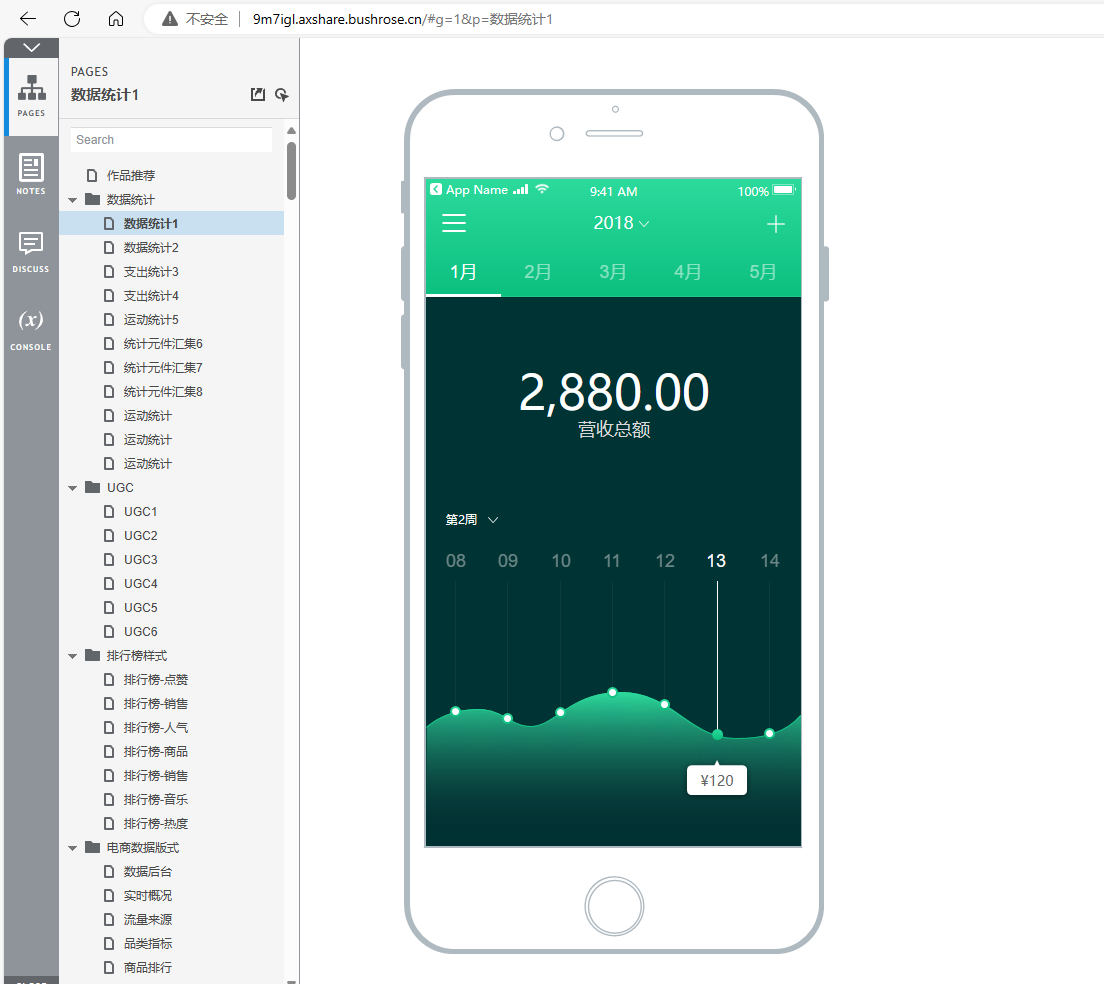
Axure Cloud如何给每个原型配置私有域名
需求 在原型发布之后,自动给原型生成一个独立访问的域名,类似http://u591bi.axshare.bushrose.cn,应该如何配置呢? 准备事项 已备案域名 如何备案?阿里云备案流程 已安装部署Axure Cloud 如何安装部署,请…...

语音模块学习——LSYT201B模组(实际操作篇)
目录 一、定制词条 二、直接用串口通信 三、使用单片机通信 理论篇在这,依旧是深圳雷龙发展的语音模块。 http://t.csdnimg.cn/2SzJL 一、定制词条 因为我想后面加到我的毕设上加个语音模块,所以定制的词条都是和芯测相关的。 动作词条播报串口输…...
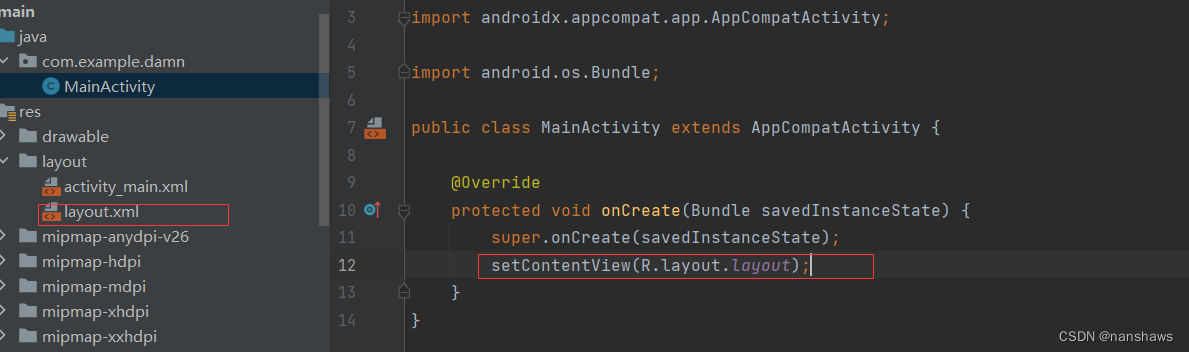
Android应用界面
概述:由于学校原因,估计会考,曹某人就浅学一下。 目录 View概念 创建和使用布局文件 相对布局 线性布局 水平线性布局 垂直线性布局 表格布局 帧布局 扁平化布局 Android控件详解 AdapterView及其子类 View概念 安卓中的View是所…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

