格密码学习笔记(二):连续极小、覆盖半径和平滑参数
文章目录
- 最短距离和连续极小值
- 距离函数和覆盖半径
- 格的平滑参数
- 致谢
最短距离和连续极小值
除了行列式,格的另一个基本量是格上最短非零向量的长度,即格中最短距离,其定义为
λ1=minx,y∈L,x≠y∥x−y∥=minz∈L,z≠0∥z∥.\begin{aligned} \lambda_1 &= \min_{\bm{x,y} \in \mathcal{L}, \bm{x} \neq \bm{y}} \| \bm{x} - \bm{y} \| \\ &= \min_{\bm{z} \in \mathcal{L}, \bm{z} \neq \bm{0}} \| \bm{z} \|. \end{aligned} λ1=x,y∈L,x=ymin∥x−y∥=z∈L,z=0min∥z∥.
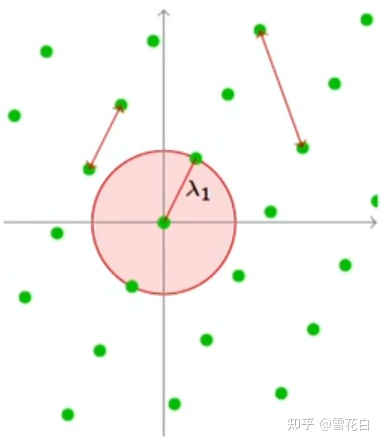
如上图所示,两两格点构成的向量都可以通过平移得到起始点为原点的向量,通过找到距离原点最近的格点即可计算出格中最短距离。格中最短距离也称为第一连续极小,记为λ1\lambda_1λ1。
同理可定义第二至第nnn连续极小λ2,…,λn\lambda_2, \dots, \lambda_nλ2,…,λn。
在二维格上,可以用多项式时间算法求解出λ1\lambda_1λ1,但在多维格上求解λ1\lambda_1λ1则十分困难。注意,给定一组格基,最短向量不一定是格基之一。
定义1 在格L\mathcal{L}L中,第iii连续极小值(i=1,…,ni=1,\dots, ni=1,…,n) 为λi=min{r:dimspan(B(r)∩L)≥i}\lambda_i = \min \{ r : \mathrm{dim} ~ \mathrm{span}(\mathcal{B}(r) \cap \mathcal{L}) \geq i \}λi=min{r:dim span(B(r)∩L)≥i}。
在定义1中,B(r)\mathcal{B}(r)B(r)表示半径为rrr的超球体(Ball),该超球体与格L\mathcal{L}L交集产生的向量张成(span\mathrm{span}span)的空间的维度(dim\mathrm{dim}dim)为iii。换而言之,第iii连续极小值即包含至少iii个线性无关格向量的最小球的半径。
把球的中心放在原点,若球中有非零格向量,那么球中不止一个格向量。以上图为例,红色区域包含了一个非零格向量以及它的逆向量,但这二者在同一条直线上,仅张成一维空间,该超球体的半径是λ1\lambda_1λ1。而以下图为例,一个更大的超球体包含了4个非零格向量,可以张成二维空间,该超球体的半径是λ2\lambda_2λ2。

在整数格Zn\mathbb{Z}^nZn中,有λ1=λ2=⋯=λn\lambda_1 = \lambda_2 = \cdots = \lambda_nλ1=λ2=⋯=λn。一般而言,λ1≤λ2⋯≤λn\lambda_1 \leq \lambda_2 \cdots \leq \lambda_nλ1≤λ2⋯≤λn。
距离函数和覆盖半径
对任意点t∈Rn\bm{t} \in \mathbb{R}^nt∈Rn,记距离函数μ(t,L)\mu(\bm{t}, \mathcal{L})μ(t,L)返回t\bm{t}t到最近格点的距离,即μ(x,L)=minx∈L∥t−x∥\mu(\bm{x}, \mathcal{L}) = \min_{\bm{x} \in \mathcal{L}} \| \bm{t} - \bm{x} \|μ(x,L)=minx∈L∥t−x∥。
通过移动t\bm{t}t可以找到μ\muμ的最大值,称为覆盖半径,即μ(L)=maxt∈span(L)μ(t,L)\mu(\mathcal{L}) = \max_{\bm{t} \in \mathrm{span}(\mathcal{L})} \mu(\bm{t}, \mathcal{L})μ(L)=maxt∈span(L)μ(t,L)。以下图为例,t\bm{t}t从①移动至②再移动至③,此时无论t\bm{t}t再怎么移动都会减小μ\muμ的值,故μ\muμ在步骤③时达到最大。
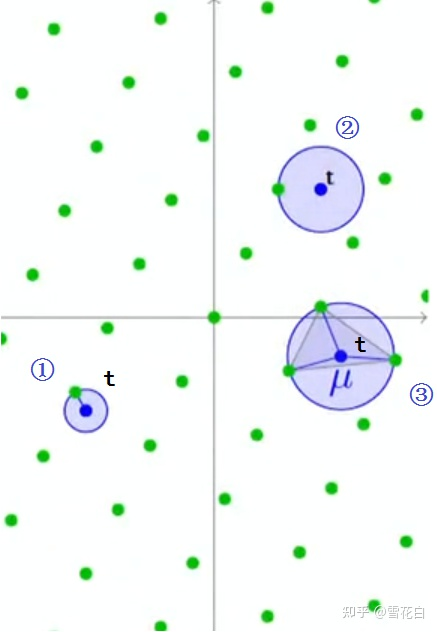
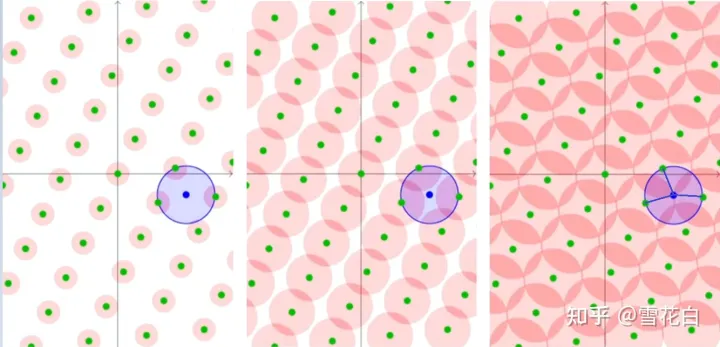
以下图为例,将所有格点作为球心,不断增大球的半径rrr,当半径rrr超过12λ1\frac{1}{2} \lambda_121λ1时这些球开始互相覆盖,而当空间中所有点都被这些球覆盖时rrr刚好等于μ\muμ的最大值,名称“覆盖半径”由此而来。想象一下,在下图的第三张子图里,若再移动蓝色点t\bm{t}t均会落在球的内部从而使μ\muμ变小。
格的平滑参数
假设噪声γ\bm{\gamma}γ随机采样自均匀分布U([0,r]n)\mathrm{U}([0, r]^n)U([0,r]n),记格点为x∈L\bm{x} \in \mathcal{L}x∈L,为使γ+x\bm{\gamma} + \bm{x}γ+x的分布看起来与U(Rn)\mathrm{U}(\mathbb{R}^n)U(Rn)无异,要使rrr足够大。以上图为例,γ+x\bm{\gamma} + \bm{x}γ+x的出现频数用红色深浅表示,当rrr太小时有些地方是空白色,随着rrr的增大有些区域红色的深浅程度不一,当rrr无穷大时所有区域颜色一样。
当rrr是无穷大时是最理想的状态。事实上,存在一个有限的r^\hat{r}r^值可使γ+x\bm{\gamma} + \bm{x}γ+x趋近于完全均匀分布,有maxμ≤∥r^∥≤log(n)⋅nλn\max \mu \leq \| \hat{r} \| \leq \log(n) \cdot \sqrt{n} \lambda_nmaxμ≤∥r^∥≤log(n)⋅nλn。
注:下面笔记属于个人猜测,高斯噪声这块公开课讲得比较模糊,强烈建议查阅原始论文。
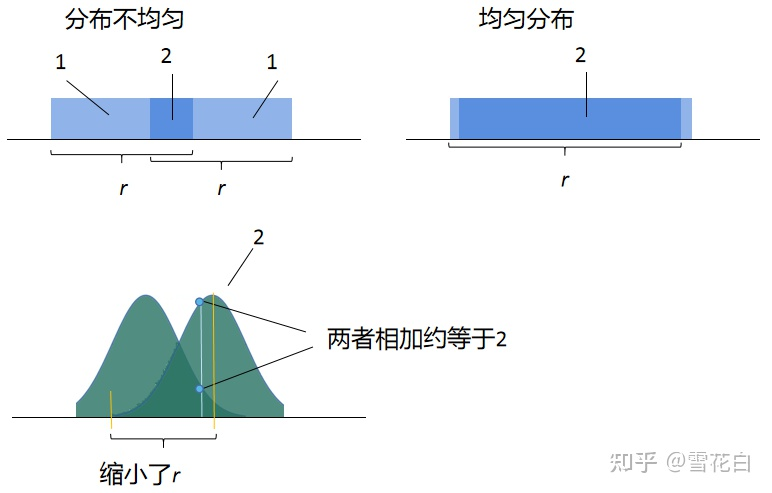
球的半径要取得很大是因为它的边界十分明显。为解决该问题,可以使球心到边界逐渐平滑,即采用球状高斯分布进行平滑,从而得到高斯噪声。以下图为例,高斯平滑缩小了rrr值。对半径对应向量的每个分量vi\bm{v}_ivi,应使得∥vi∥≈ηϵ≤log(n)λn\| \bm{v}_i \| \approx \eta_\epsilon \leq \log(n) \lambda_n∥vi∥≈ηϵ≤log(n)λn,仅略大于λn\lambda_nλn,此处ηϵ\eta_\epsilonηϵ被称为平滑参数。一般而言,ηϵ\eta_\epsilonηϵ由一个错误参数ϵ\epsilonϵ决定,ϵ\epsilonϵ表示当前噪声分布和均匀噪声分布之间的差异。
致谢
- Simons格密码公开课官网
Mathematics of Lattices - Simons Institute for the Theory of Computing
- 哔哩哔哩中英双语视频(字幕组:重庆大学大数据与软件学院 后量子密码研究小组)
【中英字幕】Simons格密码讲座第1讲:格的数学定义_哔哩哔哩_bilibili
- 其它格密码讲解课程和博文
格密码入门课程_哔哩哔哩_bilibili
格密码的基础概念_唠嗑!的博客-CSDN博客_格密码
格(Lattice)基础(一)_Amire0x的博客-CSDN博客_两组格基生成同一个格的充要条件
相关文章:

格密码学习笔记(二):连续极小、覆盖半径和平滑参数
文章目录最短距离和连续极小值距离函数和覆盖半径格的平滑参数致谢最短距离和连续极小值 除了行列式,格的另一个基本量是格上最短非零向量的长度,即格中最短距离,其定义为 λ1minx,y∈L,x≠y∥x−y∥minz∈L,z≠0∥z∥.\begin{aligned} …...

ios 通过搜索设备MAC地址绑定
最近做了一个物联网项目,涉及到了设备绑定配网这块,需要了解一下iOS BLE与设备绑定的相关知识点,第一次接触蓝牙相关的项目,所以开始熟悉蓝牙的相关信息。没有去深入研究BabyTooth库,只是感觉CoreBluetooth已经让我更好的理解整个流程这个物联网项目的设备绑定流程是…...

Python实现人脸识别,进行视频跟踪打码,羞羞的画面统统打上马赛克
哈喽兄弟们,我是轻松~ 今天我们来实现用Python自动对视频打马赛克前言准备工作代码实战效果展示最后前言 事情是这样的,昨天去表弟家,用了下他的电脑,不小心点到了他硬盘里隐藏的秘密,本来我只需要用几分钟电脑的&…...

vcf bed起始位置是0还是1
VCF 起始位置为1, POS - position: The reference position, with the 1st base having position 1. Positions are sorted numerically, in increasing order, within each reference sequence CHROM. It is permitted to have multiple records with the same POS. Telome…...
Hexo+live2d | 如何把live2d老婆放进自己的博客
参考:Hexo添加Live2D看板娘最新教程live2d-widgetlive2d-widget-models网页/博客Hexo添加live2d游戏角色看板娘,简易添加,碧蓝航线等live2d新型游戏角色模型(moc3)live2d-moc3jsdelivr方法1可以直接去看参考文章的第一部分的第一篇…...

【微信小程序】-- 页面导航 -- 导航传参(二十四)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

Pytorch学习笔记#2: 搭建神经网络训练MNIST手写数字数据集
学习自https://pytorch.org/tutorials/beginner/basics/quickstart_tutorial.html 导入并预处理数据集 pytorch中数据导入和预处理主要用torch.utils.data.DataLoader 和 torch.utils.data.Dataset Dataset 存储样本及其相应的标签,DataLoader在数据上生成一个可迭…...

C语言 猜名次、猜凶手、杨辉三角题目详解
猜名次题目:5位运动员参加了10米台跳水比赛,有人让他们预测比赛结果:A选手说:B第二,我第三;B选手说:我第二,E第四;C选手说:我第一,D第二ÿ…...

蚁群算法负荷预测
%% 清空环境变量 clc clear close all format compact %% 网络结构建立 %% 清空环境变量 clc clear close all format compact %% 网络结构建立 %读取数据 dataxlsread(天气_电量_数据.xlsx,C12:J70);%前7列为每个时刻的发电量 最后列为天气 for i1:58 input(i,:)[data…...

ubuntu添加系统服务实现开机root权限运行
需求 开机自动运行程序(或脚本),需要以root权限运行但不输入密码,也不能将密码写入文件。 环境 Ubuntu 20.04 解决方案 添加系统服务,然后通过systemctl控制。 操作步骤 假设目标程序为/home/xxx/test 1、创建service配置文件 [Unit…...

【阅读笔记】你不知道的Javascript--类与类型委托3
目录类一些常见原理混入行为委托委托理论类与对象更妙的设计与语法类型冷门关键词typeof 防范机制值原生函数访问内部属性类 一些常见原理 在继承或者实例化时,JavaScript 的对象机制并不会自动执行复制行为; 多态:JS 中的多态,…...
文件服务设计
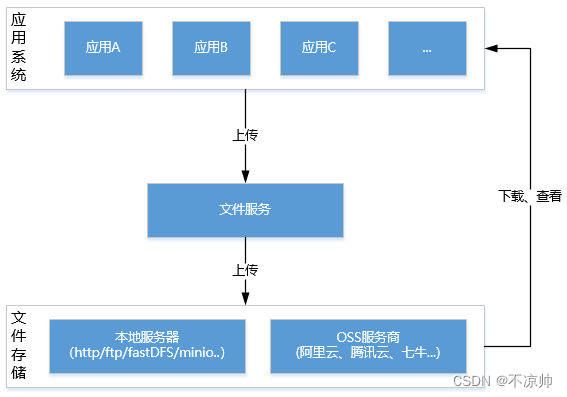
一、需求背景 文件的上传、下载功能是软件系统常见的功能,包括上传文件、下载文件、查看文件等。例如:电商系统中需要上传商品的图片、广告视频,办公系统中上传附件,社交类系统中上传用户头像等等。文件上传下载大致流程为&#…...

【批处理脚本】-1.22-字符串界定符号 ““
"><--点击返回「批处理BAT从入门到精通」总目录--> 共3页精讲(列举了所有字符串界定符号 ""的用法,图文并茂,通俗易懂) 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中,经常会在其集成开发环境IDE(CodeWarrior,S32K DS,Davinci,…...

【Flutter·学习实践·UI篇】基础且重要的UI知识
前言 参考学习官网:《Flutter实战第二版》 学习前先记住:Flutter 中万物皆为Widget,心中默念3次以上铭记于心。 这一点和开发语言Dart的变量一切皆是对象的概念,相互对应。 Widget 在前面的介绍中,我们知道在Flutt…...

【OpenCV】车牌自动识别算法的设计与实现
写目录一. 🦁 设计任务说明1.1 主要设计内容1.1.1 设计并实现车牌自动识别算法,基本功能要求1.1.2 参考资料1.1.3 参考界面布局1.2 开发该系统软件环境及使用的技术说明1.3 开发计划二. 🦁 系统设计2.1 功能分析2.1.1 车辆图像获取2.1.2 车牌…...

SpringBoot发送邮件
目录1. 获取授权码2. jar包引入3. 配置application4. 代码实现1. 获取授权码 以126邮箱为例,点开设置,选择POP3/SMTP/IMAP 开启POP3/SMTP服务,新增授权密码 扫码二维码,发送要求的短信内容到指定的号码即可,然后会返回…...
BigInteger类和BigDecimal类的简单介绍
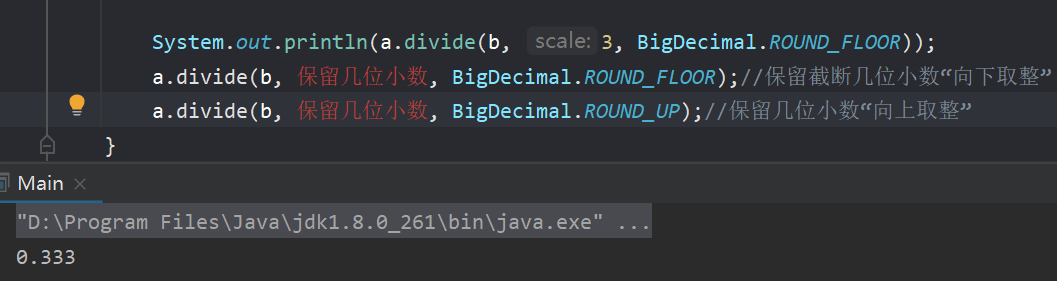
文章目录📖前言:🎀BigInteger类和BigDecimal类的由来🎀BigDecimal类的优点🎀BigDecimal类容易引发的错误🏅处理方法📖前言: 本篇博客主要介绍BigInteger类和BigDecimal类的用途及常…...
mysql五种索引类型---实操版本
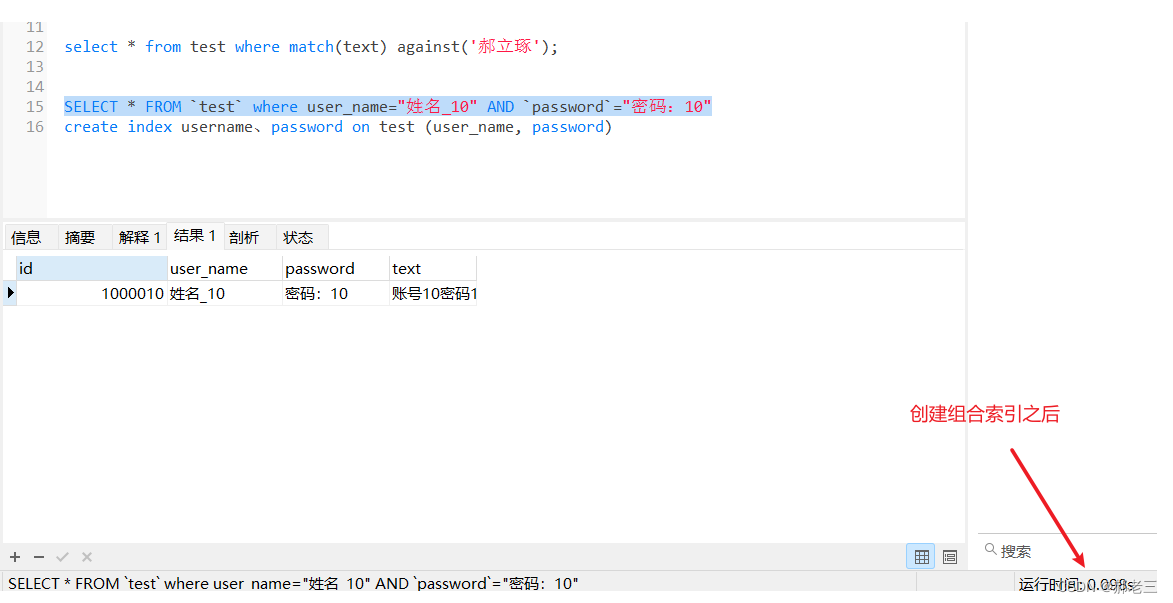
背景 最近学习了Mysql的索引,索引对于Mysql的高效运行是非常重要的,正确的使用索引可以大大的提高MySql的检索速度。通过索引可以大大的提升查询的速度。不过也会带来一些问题。比如会降低更新表的速度(因为不但要把保存数据还要保存一下索引…...

【微信小程序】-- 页面导航 -- 编程式导航(二十三)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

路由追踪工具 traceroute 使用技巧
路由追踪工具 traceroute 使用技巧路由追踪工作原理路由追踪实例1. 如何运行 traceroute2. 禁用 IP 地址和主机名映射3. 配置回复等待时间4. 配置每一跳的查询次数5. 配置 TTL 值我想知道一个数据包从出发地到目的地所遵循的路由,即所有转发实体(中间的路…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
