【图论】树链剖分
本篇博客参考:
- 【洛谷日报#17】树链剖分详解
- Oi Wiki 树链剖分
文章目录
- 基本概念
- 代码实现
- 常见应用
- 路径维护:求树上两点路径权值和
- 路径维护:改变两点最短路径上的所有点的权值
- 求最近公共祖先
基本概念
首先,树链剖分是什么呢?
简单来说,就是把一棵树分成很多条链,然后利用数据结构(线段树、树状数组)维护链上的信息
下面是一些定义:
- 重子结点:父亲结点的所有儿子结点中子树结点数目最多的结点称为重子结点
- 轻子结点:父亲结点的所有儿子中除了重子结点的其他结点称为轻子结点
如果某个结点是叶子结点,那么它既没有重子结点也没有轻子结点
- 重边:父亲结点和重子结点连成的边
- 轻边:父亲结点和轻子结点连成的边
- 重链:多条重边连接成的链
- 轻链:多条轻边连接成的链
落单的点也当做重链,那整棵树就会被分成若干条重链,类似这样:(图源Oi Wiki)
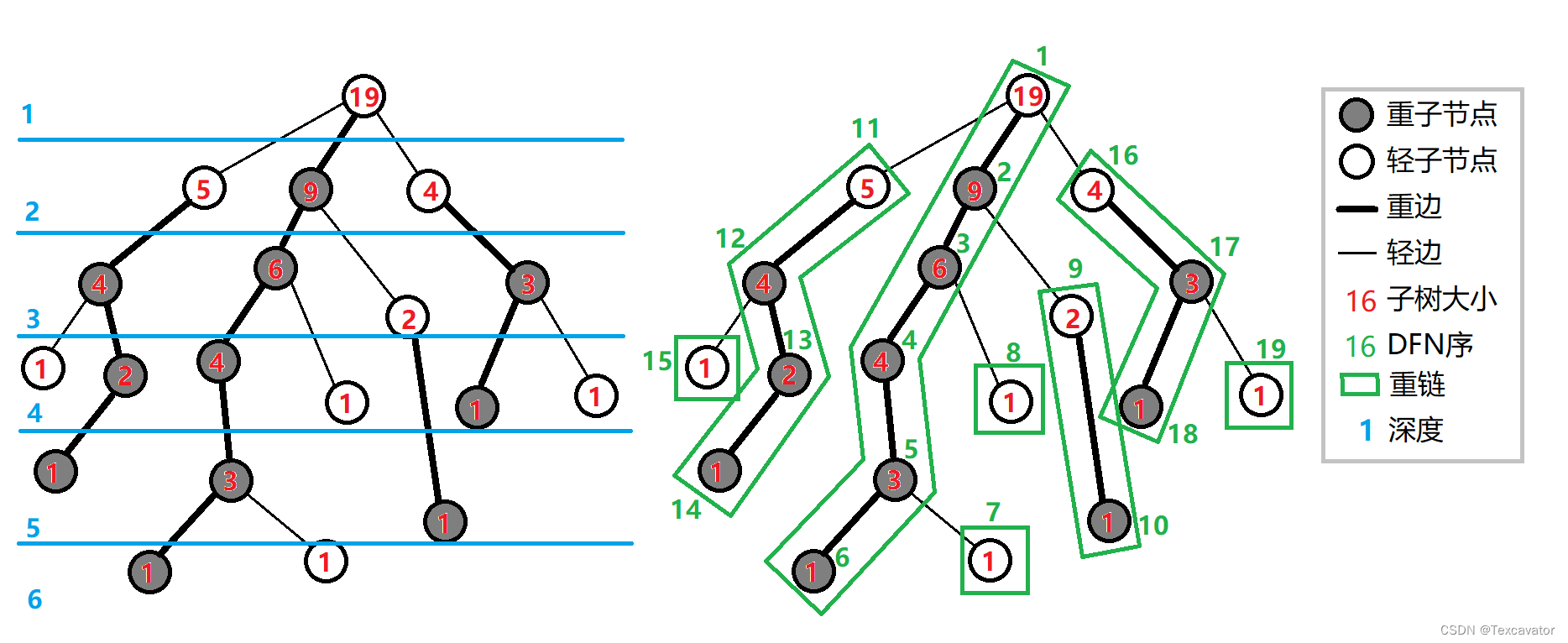
下面是一些变量声明:
fa[u]结点 u 的父亲结点dep[u]结点 u 的深度sz[u]以结点 u 为根的子树的结点个数son[u]结点 u 的重儿子top[u]结点 u 所在链的顶端结点dfn[u]结点 u 在 dfs 中的执行顺序,同时也是树链剖分后的新编号,可以理解为dfs序的映射id[u]dfn 标号 u 对应的结点编号,有id[dfn[u]] == u
树链剖分的一些性质
- 重链开头的结点不一定是重子结点(因为每一个非叶子结点不管是重子结点还是轻子结点都有重边)
- 剖分时重链优先遍历,最后的 dfs 序中(也就是
dfn数组),重链的 dfs 序时连续的,按 dfs 序排序后的序列就是剖分后的链 - 时间复杂度 O ( l o g n ) O(logn) O(logn)
代码实现
接下来需要实现树链剖分,也就是把每个结点划到一条链里,这通常是由两边 dfs 来实现的
第一遍 dfs
目的:处理 fa[u] dep[u] sz[u] son[u]
void dfs1(int u, int father, int depth) // u: 当前结点 fa: 父结点 depth: 当前深度
{fa[u] = father; // 更新当前结点父结点dep[u] = depth; // 更新当前结点深度sz[u] = 1; // 子树大小初始化为1for (int i = 0; i < g[u].size(); i ++ ){int j = g[u][i]; // 子结点编号if (j == father) continue;dfs1(j, u, depth + 1);sz[u] += sz[j]; // 用子结点的sz更新父结点的szif (sz[j] > sz[son[u]]) son[u] = j; // 更新重子结点}
}
第二遍 dfs
目的:处理 top[u] dfn[u] id[u]
void dfs2(int u, int tt) // u: 当前结点 tt: 重链顶端结点
{top[u] = tt; // 更新当前结点所在重链顶端dfn[u] = ++ cnt; // 更新dfs序id[cnt] = u; // 更新dfs序的映射if (!son[u]) return; // 叶子结点 直接退出// 优先遍历重子结点 目的是保证链上各个结点的dfs序连续// 当前结点的重子结点和当前结点在同一条链上 所以链的顶端都是ttdfs2(son[u], tt); for (int i = 0; i < g[u].size(); i ++ ){int j = g[u][i]; // 子结点编号if (j == son[u] || j == fa[u]) continue; // 遇到重子结点或者父结点就跳过dfs2(j, j); // j点位于轻链顶端 它的top必然是本身}
}
常见应用
两遍 dfs 之后,就已经完成了树链剖分的操作,但是由于本人举一反三能力缺失根本不知道应该怎么用,所以后面再放几个常见的使用情况
路径维护:求树上两点路径权值和
这里做的是一个类似LCA的操作,如果两个结点不在同一条链上,就让深度更大的结点往上跳(每次只能跳一个结点,避免两个结点一起跳导致擦肩而过)直到跳到同一条链上,因为同一条链上的点 dfs 序是相邻的,所以可以直接在这条链上用数据结构计算权值和(下面的代码用的是线段树)
int sum(int x, int y) // xy表示待求的两点路径权值和
{int ans = 0;int tx = top[x], ty = top[y]; // tx ty分别表示x和y所在重链的顶端结点while (tx != ty) // 让x和y跳到同一条链上{if (dep[x] >= dep[y]) // x比y更深 让x先跳{ans += query(dfn[tx], dfn[x]); // query是线段树的区间求和函数x = fa[tx], tx = top[x]; // 让x跳到原先链顶端的父结点 更新tx}else{ ans += query(dfn[ty], dfn[y]); // query是线段树的区间求和函数y = fa[ty], ty = top[y]; // 让y跳到原先链顶端的父结点 更新ty}}// 循环结束 x和y终于到了同一条链 但是二者不一定是同一个结点 所以还需要计算两点之间的贡献if (dfn[x] <= dfn[y]) ans += query(dfn[x], dfn[y]);else ans += query(dfn[y], dfn[x]);return ans;
}
路径维护:改变两点最短路径上的所有点的权值
和上面的求最短路径权值和很像,都是先让两个点跳到同一条链上再进行计算
void update(int x, int y, int c) // 把x与y的最短路上所有点的权值都加上c
{int tx = top[x], ty = top[y];while (tx != ty){if (dep[tx] >= dep[ty]){modify(dfn[tx], dfn[x], c); // modify是线段树区间修改的函数x = fa[tx], tx = top[x]; // 让x跳到原先链顶端的父结点 更新tx}else{modify(dfn[ty], dfn[y], c); // modify是线段树区间修改的函数y = fa[ty], ty = top[y]; // 让y跳到原先链顶端的父结点 更新ty}}// 循环结束 x和y终于到了同一条链 但是二者不一定是同一个结点 所以还需要对两点之间的结点进行修改if (dfn[x] <= dfn[y]) modify(dfn[x], dfn[y], c);else modify(dfn[y], dfn[x], c);
}
求最近公共祖先
思路就是,如果两个点不在一条重链上,那就不断让深度大的结点往上跳,直到跳到同一条链上,那么深度较小的点就是LCA
int lca(int u, int v) // 求u和v的lca
{while (top[u] != top[v]) // 如果u和v不在同一条链上就一直让深度大的点往上跳{if (dep[top[u]] > dep[top[v]]) u = fa[top[u]];else v = fa[top[v]];}return dep[u] > dep[v] ? v : u; // 深度小的结点就是lca
}
相关文章:

【图论】树链剖分
本篇博客参考: 【洛谷日报#17】树链剖分详解Oi Wiki 树链剖分 文章目录 基本概念代码实现常见应用路径维护:求树上两点路径权值和路径维护:改变两点最短路径上的所有点的权值求最近公共祖先 基本概念 首先,树链剖分是什么呢&…...

Requests教程-17-请求代理设置
上一小节我们学习了requests解决乱码的方法,本小节我们讲解一下requests设置代理的方法。 代理基本原理 代理实际上指的就是代理服务器, 英文叫作proxy server ,它的功能是代理网络用户去取得网络信息。形象地说,它是网络信息的中…...

python内置函数 G
python内置函数 G Python 解释器内置了很多函数和类型,任何时候都能使用。 G 名称描述getattr从对象中获取属性值。globals返回当前全局符号表的字典。 getattr(object, name) getattr(object, name) getattr(object, name, default) getattr() 是 Python 中…...
深入了解 Spring boot的事务管理机制:掌握 Spring 事务的几种传播行为、隔离级别和回滚机制,理解 AOP 在事务管理中的应用
🎉🎉欢迎光临,终于等到你啦🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟持续更新的专栏《Spring 狂野之旅:从入门到入魔》 &a…...

机械产品CE-MD认证测试项目介绍
机械产品CE-MD认证测试项目介绍 一、引言 随着欧洲市场的日益开放和全球化进程的加速,越来越多的机械产品进入欧洲市场。为确保这些产品的安全性和符合性,欧洲联盟(EU)引入了CE认证制度。同时,对于医疗器械类产品&…...
金融知识分享系列之:MACD指标精讲
金融知识分享系列之:MACD指标精讲 一、MACD指标二、指标原理三、MACD指标参考用法四、MACD计算步骤五、MACD分析要素六、根据快线DIF位置判断趋势七、金叉死叉作为多空信号八、快线位置交叉信号九、指标背离判断行情反转十、差离值的正负十一、差离值的变化十二、指…...

王道c语言-100元有几种换法
Description 一张面值100元的人民币换成10元、5元、2元和1元面值的票子。要求换正好40张,且每种票子至少一张。问:有几种换法? #include <stdio.h> int main() {int count 0;int i, j, t, k, ret 0;for (i 1; i < 37; i) {for …...

c++野指针如何处理?
什么是野指针? 野指针指向一个已删除的对象或未申请访问受限内存区域的指针。与空指针不同,野指针无法通过简单地判断是否为NULL避免,而只能通过养成良好的编程习惯来尽力减少,对野指针进行操作很容易造成程序错误。 野指针产生…...
关于大根堆,set重载运算符
题目描述 \,\,\,\,\,\,\,\,\,\,制定合理的日程能够帮助利用好时间进行加训,加训和加训。 \,\,\,\,\,\,\,\,\,\,新学期开始了,应该好好学习了!凌晨两点整,加睡失败的你在为新一天的各项重要事件制定闹钟。 \,\,\,\,\,\,\,\,\,\, \,…...

Algae c++
描述 问题陈述 池塘中藻类的发展情况如下。 假设年初i水藻的总重量为xi克。对于 i≥2000,下列公式成立: xi1rxi−D 给你r、D和x2000。请依次计算 x2001、...、x2010 并打印出来。 输入描述 输入内容由标准输入法提供,格式…...

开发常用的一些工具总结
开发常用的一些工具总结 记录一些常用的开发软件. Android 开发相关 : Android studio 安卓开发者必备的编辑器,也是我用过最好用的编辑器.还可以用来写JNI 和C.Android studio 插件 : GsonFormatLeakCanary 其他 VS Code :轻量级的开发工具,插件非常多,很好用,但是上手难度…...

k8s Yaml语法解析
YAML是一个类似 XML、JSON 的标记性语言。它强调以数据为中心,并不是以标识语言为重点。因而YAML本身的定义比较简单,号称"一种人性化的数据格式语言"。 YAML的语法比较简单,主要有下面几个: 1、大小写敏感 2、使用缩进…...

【晴问算法】提高篇—动态规划专题—最长公共子序列
题目描述 现有两个字符串s1与s2,求s1与s2的最长公共子序列的长度(子序列可以不连续)。 输入描述 第一行为字符串s1,仅由小写字母组成,长度不超过100; 第一行为字符串s2…...

Greetings
Problem - 1915F - Codeforces 题意 给一些(l,r)找到所有能够包含(l,r)的数目 引入 也就是找逆序对个数 要用到归并排序中的思想: //https://www.luogu.com.cn/problem/P1216 #include<iostream> #include<cstdio> #include<stack> #include…...

JS03-函数
函数 使用函数 // 函数声明function sayHi(){document.write(Hello!<br>)}for(let i 1; i < 6; i){// 函数调用sayHi()}函数封装 function getScore(arr){sum 0for( let i 0; i < arr.length; i){sum arr[i]}document.write(sum)}getScore([99, 66, 100])函数…...
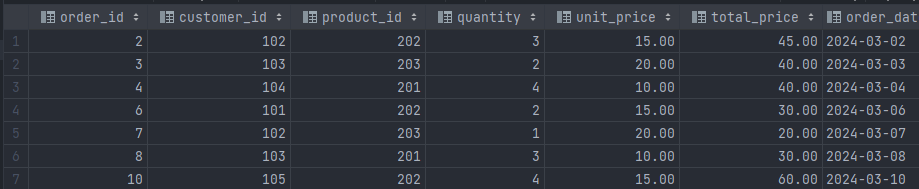
MySQL | CRUD
目录 1. Create 2. Retrieve 2.1. SELECT列 2.1.1. 全列查询 2.1.2. 指定列查询 2.1.3. 查询字段为表达式 2.1.4. 为查询结果指定别名 2.1.5. 结果去重 2.2. WHERE条件 2.2.1. 年龄小于19的同学 2.2.2. id在2~3的同学 2.2.3. id为1和4的同学 2.2.4. 姓张的同学及张…...

【电路笔记】-MOSFET作为开关
MOSFET 作为开关 文章目录 MOSFET 作为开关1、概述2、MOSFET特性曲线2.1 截住区域2.2 饱和区域3、MOSFET作为开关的示例4、功率MOSFET电机控制5、P沟道MOSFET作为开关6、互补MOSFET作为开关电机控制器当 MOSFET 在截止区和饱和区之间工作时,MOSFET 是非常好的电子开关,用于控…...

SpringBoot+Vue项目(Vue3环境搭建 + 基础页面)
文章目录 1.项目基本介绍2.安装Node.js(SSM部分安装过)3.初始化前端工程1.创建一个文件夹 springboot_vue2.创建vue项目1.在刚才创建的文件夹下打开命令行,使用脚手架搭建项目2.选择手动配置3.选择三个4.选择vue35.选择路由模式6.选择包管理方…...

elementui el-table表格自动循环滚动【超详细图解】
效果如图 1. 当表格内容超出时,自动滚动,滚动到最后一条之后在从头滚动。 2. 鼠标移入表格中,停止滚动;移出后,继续滚动。 直接贴代码 <template><div><div class"app-container"><e…...

关于学习的一点粗浅见解
我们学习的每一个领域,大多都有着宽泛的知识面,那在学习过程中,我们是应该一开始就专钻一个方向(即深度),还是应该先扩展知识面(即广度)?个人认为,应该先扩展知识面宽度,然后再精研某个方向&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
