计算机网络——物理层(奈氏准则和香农定理)
计算机网络——物理层(奈氏准则和香农定理)
- 失真
- 码间串扰
- 奈氏准则(奈奎斯特定理)
- 极限数据率
- 噪声
- 信噪比
- 香农定理
- 奈氏准则和香农定理的区别
前面我们已经了解一些数据通信的基本知识,没有看过上一篇得小伙伴可以点击这里:
https://blog.csdn.net/qq_67693066/article/details/136685045
今天我们来学习两个准则——奈氏准则和香农定理:
失真
失真: 是指信号在传输过程中的衰减或扭曲。当信号通过通信通道或传输媒介时,由于噪声、衰减或反射等因素,信号可能会发生失真。失真导致信号的波形形状发生变化,从而影响数据的准确性和可靠性。
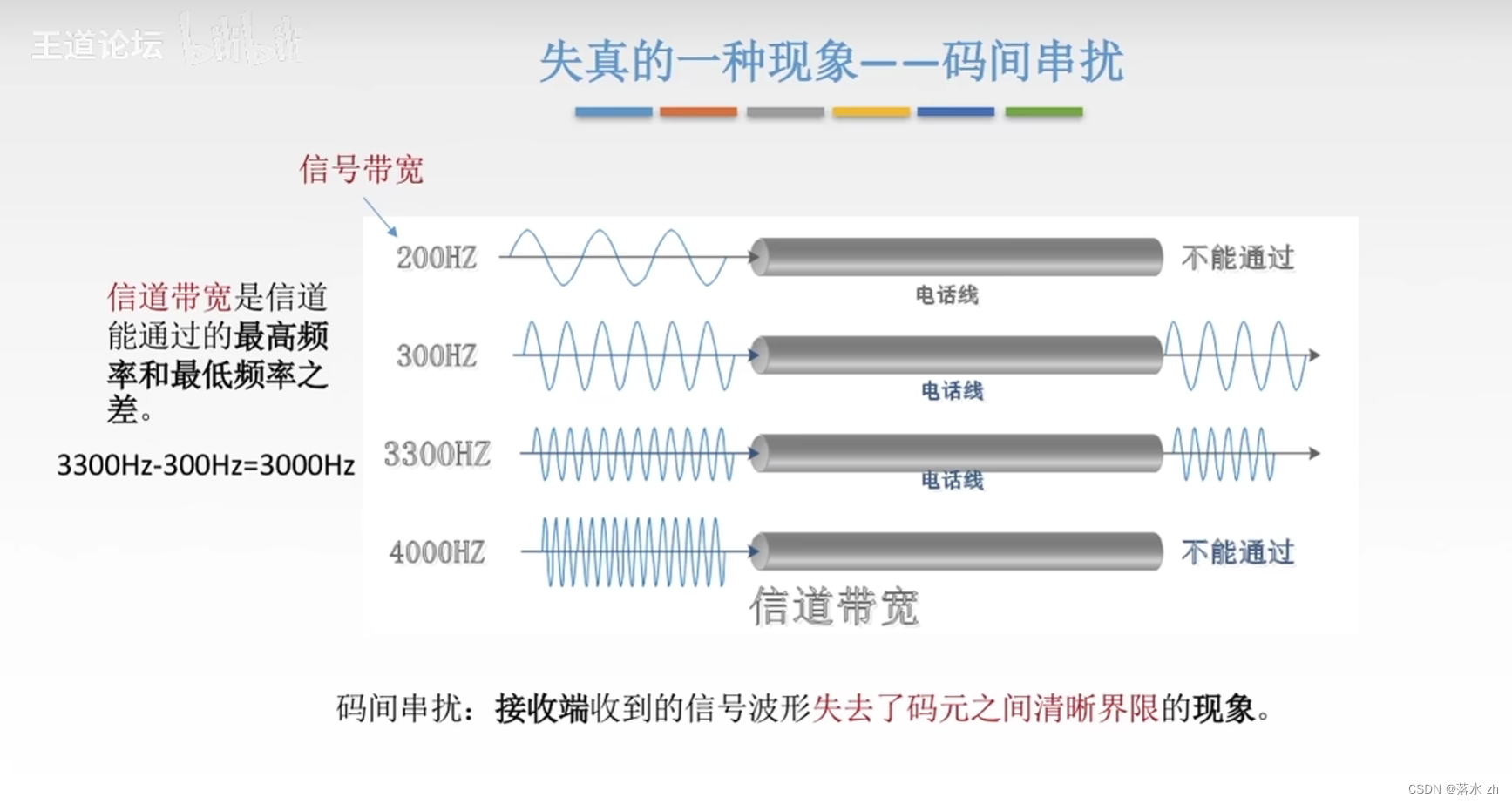
码间串扰
码间串扰(Inter-Symbol Interference,ISI)是数字通信中常见的一种失真形式,它发生在相邻码元之间的干扰导致信号间隔模糊,从而使接收端难以准确识别每个码元。
这里注意一下,这里的信号带宽过高过低都不行。过低会导致数据没传过去就消磨干净了,过高会导致码元过于紧密导致无法识别。
奈氏准则(奈奎斯特定理)
奈氏准则,也被称为奈奎斯特定理,是1924年由奈奎斯特推导出的准则。它主要描述了在理想低通(即无噪声、带宽受限)的信道中,为了避免码间串扰,码元的传输速率的上限值。具体地,极限码元传输速率为2WBaud,其中W是理想低通信道的带宽,单位为Hz;Baud是波特
极限数据率
奈氏准则倒是不难,但是这个极限数据率会结合奈氏准则,这个就会和香农定理搞混:
奈氏准则(奈奎斯特定理)为极限数据率提供了一个重要的理论基础。在理想低通(无噪声、带宽有限)的信道中,为了避免码间串扰,极限码元传输速率为2W波特,其中W是信道的带宽。进一步地,如果V表示每个码元离散电平的数目(即码元可以表示的不同状态的数量),则理想低通信道下的极限数据传输速率可以通过公式2Wlog2V来计算,单位为b/s(比特每秒)。这个公式表明,信道的带宽越宽,或者每个码元所能表示的信息量越大,那么数据的极限传输速率就越高。
举个例子:
噪声
噪声是指在信号传输过程中,由于各种原因而产生的干扰或杂音。这些干扰或杂音可能会影响信号的质量和可靠性,导致信息传输错误或失真噪声可能来自多种源头,包括电子设备、传输介质以及自然环境等。为了降低噪声对信号传输的影响,通信系统通常会采用一系列技术,如信号调制、纠错码和滤波器等,以提高信号传输的质量和可靠性。
信噪比
信噪比 SNR或S/N是指一个电子设备或者电子系统中信号与噪声的比例,是用来描述信号中有效成分与噪声成分的比例关系的参数。信噪比的计量单位是dB,其数值越高,代表信号中的噪声越小,信号质量越好。
对于一张图像来说,信噪比高意味着画面干净无噪点,而信噪比低则会使图像粗糙噪声多,画面发灰不通透,对比度不够。同样,对于音频来说,信噪比高意味着音频质量纯净,噪声少。
信噪比广泛应用于许多领域,如生物学、通信科技等,其定义随应用背景的不同而有所变化,但都围绕着有效信息与噪声之间的关系。
香农定理
上面的奈氏准则是建立在无噪声、带宽有限的情况之下。而香农定理是建立在带宽有限,有噪声的前提下:
香农定理:描述了有限带宽、有随机热噪声信道的最大传输速率与信道带宽、信号噪声功率比之间的关系(通过公式C=Wlog2(1+S/N)来计算可得到的链路速度,其中C是链路速度,W是链路带宽,S是平均信号功率,N是平均噪声功率,信噪比(S/N)通常用分贝(dB)表示。)。具体来说,它指出在给定信道条件下存在一个极限数据传输速率。
举个例子:

奈氏准则和香农定理的区别

相关文章:

计算机网络——物理层(奈氏准则和香农定理)
计算机网络——物理层(奈氏准则和香农定理) 失真码间串扰奈氏准则(奈奎斯特定理)极限数据率 噪声信噪比香农定理奈氏准则和香农定理的区别 前面我们已经了解一些数据通信的基本知识,没有看过上一篇得小伙伴可以点击这里…...

XML语言的学习记录3-解析
学习笔记: 一、 解析XML文档: 1.使用 XMLHttpRequest 对象,将xml文档放入XML DOM对象中: xmlhttpnew XMLHttpRequest(); xmlhttp.open("GET","books.xml",false); xmlhttp.send(); xmlDocxmlhttp.response…...

【Linux】cat vim 命令存在着什么区别?
Linux 中的 cat 命令和 vim 命令之间存在一些显著的区别! cat 命令 首先,cat命令主要用于连接并显示文件的内容。它的原含义是“连接(concatenate)”,可以将多个文件的内容连接起来,并输出到标准输出流中&…...
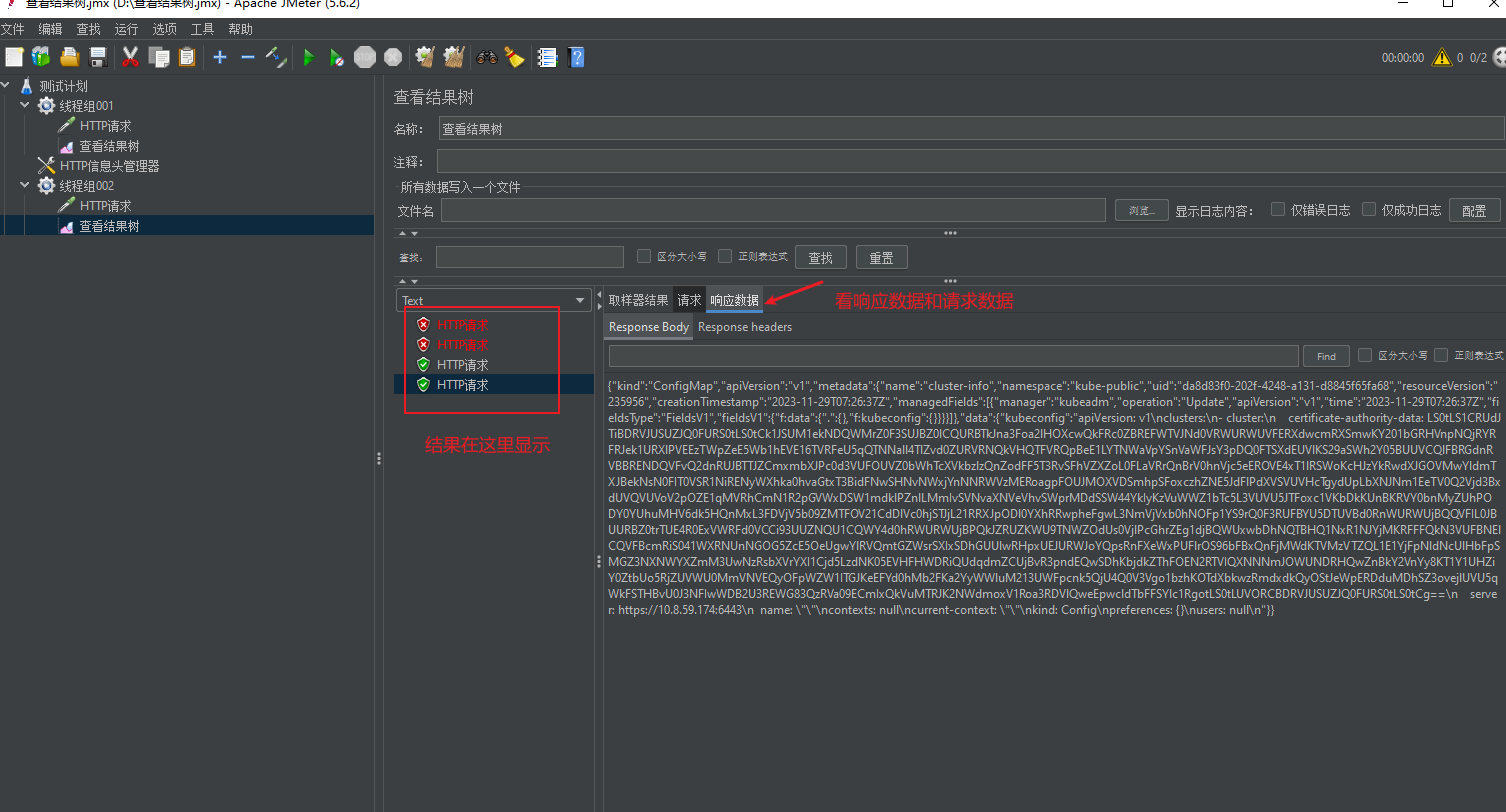
MeterSphere和Jmeter使用总结
一、MeterSphere 介绍 MeterSphere 是⼀站式开源持续测试平台,涵盖测试跟踪、接⼝测试、UI 测试和性能测试等,全 ⾯兼容 JMeter、Selenium 等主流开源标准,能够有效助⼒开发和测试团队在线共享协作,实现端到 端的测试管理跟踪…...
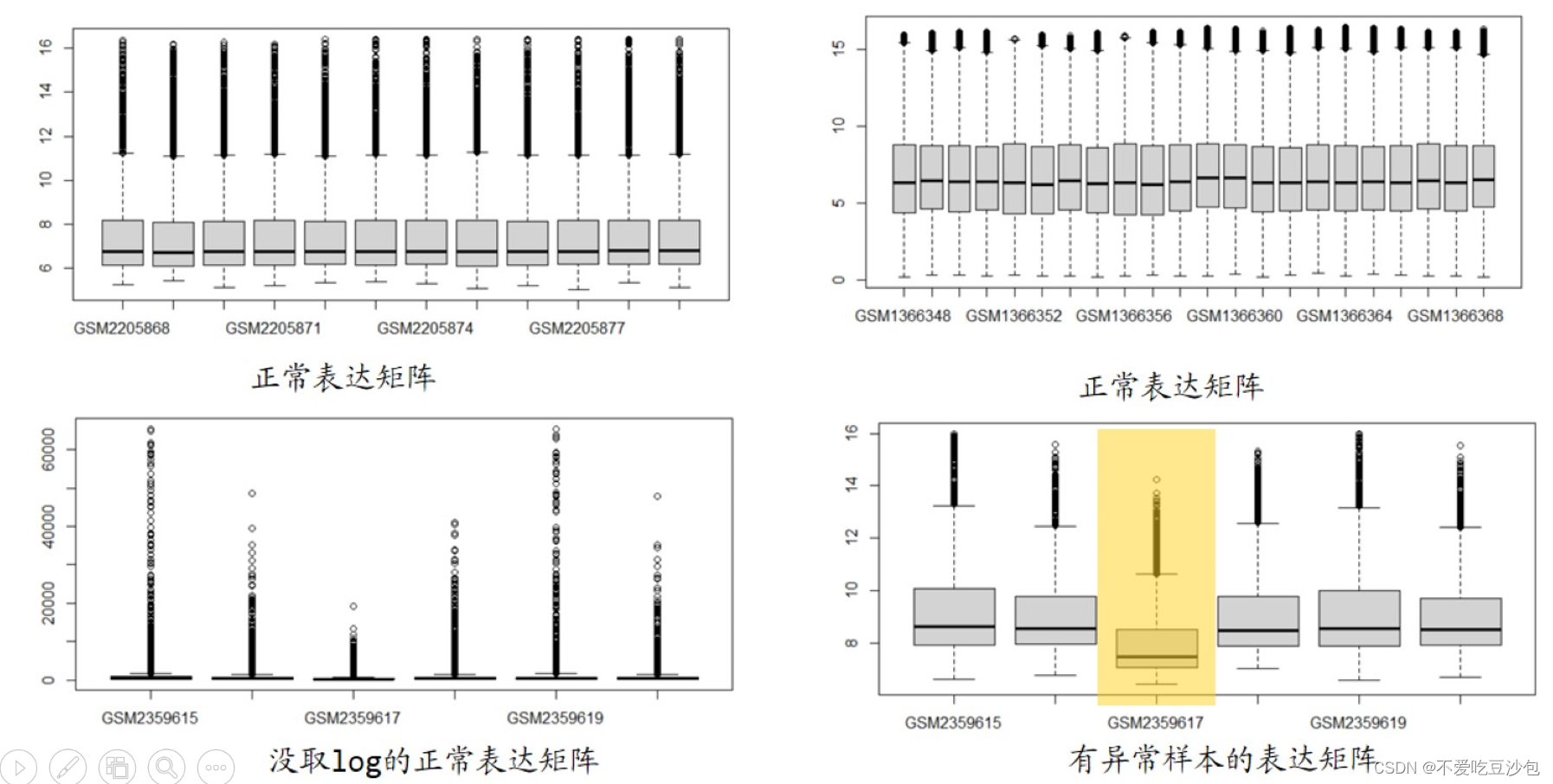
学习笔记Day8:GEO数据挖掘-基因表达芯片
GEO数据挖掘 数据库:GEO、NHANCE、TCGA、ICGC、CCLE、SEER等 数据类型:基因表达芯片、转录组、单细胞、突变、甲基化、拷贝数变异等等 常见图表 表达矩阵 一行为一个基因,一列为一个样本,内容是基因表达量。 热图 输入数据…...

如何将大华dav视频转mp4?一键无损清晰转换~
Digital Audio Video(DAV)文件格式源于数字监控领域,旨在解决视频监控数据的存储和回放问题。随着数字监控技术的发展,DAV格式逐渐成为监控设备记录视频的标准格式,广泛应用于安防系统、摄像头监控等场景。 MP4文件格式…...

数字化转型导师坚鹏:人工智能在金融机构数字化转型中的应用
人工智能在金融机构数字化转型中的应用 课程背景: 金融机构数字化转型离不开人工智能,在金融机构数字化转型中,人工智能起到至关重要的作用,很多机构存在以下问题: 不清楚人工智能产业对我们有什么影响?…...
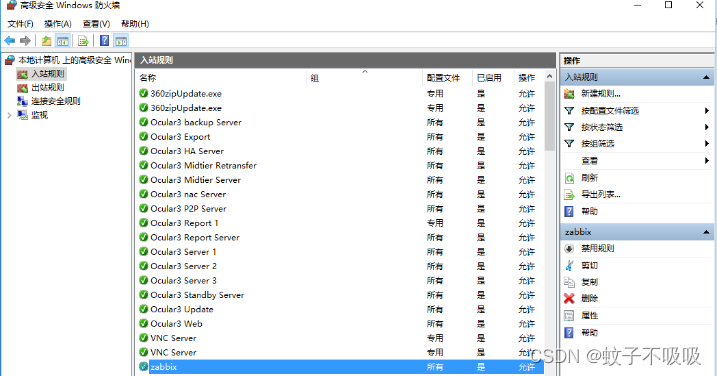
部署Zabbix Agents添加使能监测服务器_Windows平台_MSI/Archive模式
Windows平台 一、从MSI安装Windows代理,添加Windows Servers/PC 概述 可以从Windows MSI安装包(32位或64位) 安装Zabbix agent 32位包不能安装在64位Windows中 所有软件包都支持TLS,配置TLS可选 支持UI和命令行的安装。 1、下载Agent代理程序,使用Agent2升级版,官网链接如…...

十一 超级数据查看器 讲解稿 详情6 导出功能
十一 超级数据查看器 讲解稿 详情6 导出功能 点击此处 以新页面 打开B站 播放当前教学视频 app下载地址 百度手机助手 下载地址4 讲解稿全文: 导出功能讲解 这节课我们讲解一下导出功能, 导出功能,可以将当前查到的信息导出成E…...

java遍历文件目录去除中文文件名
文章目录 一、原始需求二、maven依赖三、核心代码四、运行结果 一、原始需求 需要遍历文件目录及其子目录,找出包含中文字符的文件名,将中文字符去除。 二、maven依赖 pom.xml <dependency><groupId>org.apache.commons</groupId>&…...
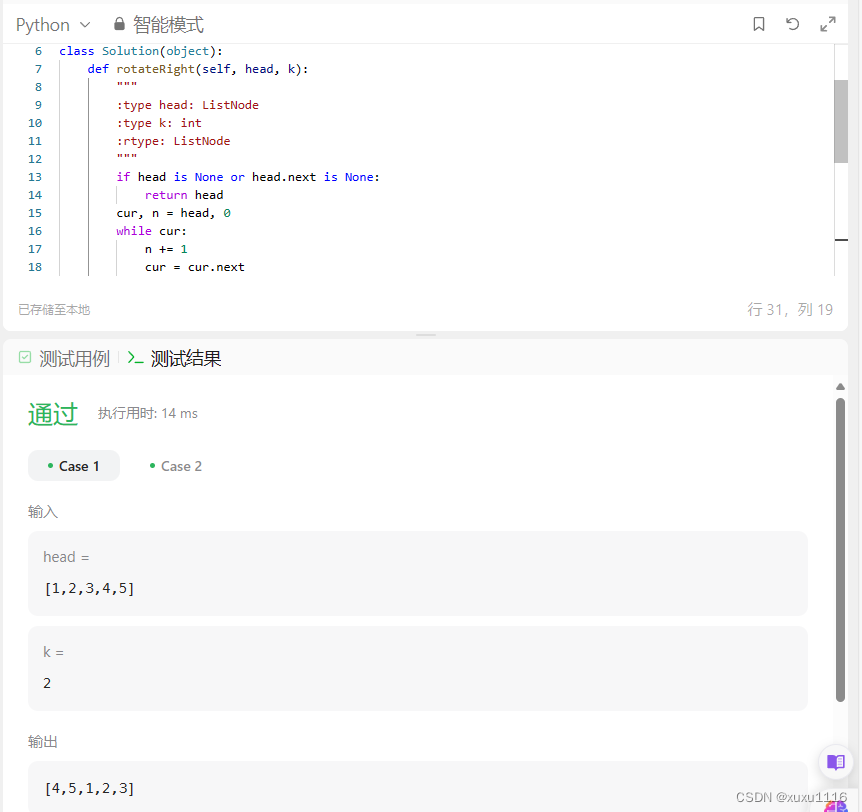
LeetCode Python - 61. 旋转链表
目录 题目描述解法运行结果 题目描述 给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。 示例 1: 输入:head [1,2,3,4,5], k 2 输出:[4,5,1,2,3] 示例 2: 输入:head…...

k8s client-java创建pod常见问题
1.配置Kubernetes连接: 使用Kubernetes的配置文件(通常位于~/.kube/config)或直接使用API服务器地址、认证信息等来配置客户端。 配置通常有两种模式,安全和不安全的配置模式,对认证要求严格就选用安全模式ÿ…...

C++——字符串、读写文件、结构体、枚举
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...
vscode 运行 java 项目之解决“Build failed, do you want to continue”的问题
Visual Studio Code运行 java 起来似乎比 IDEA 更轻量、比 eclipse 更友好,是不可多得的现代编译法宝。 安装好官方推荐的 java 扩展包后,就可以运行 java 代码了。功能 比 code runner 强,支持 gradle、maven、普通java项目,运行…...
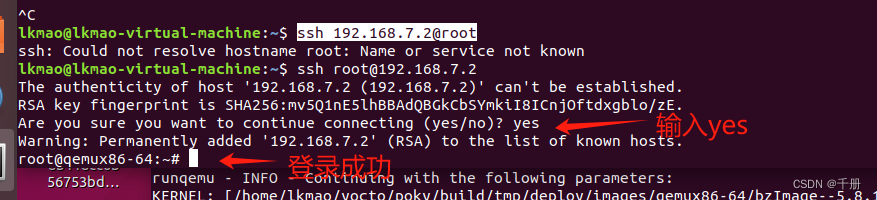
yocto编译测试
源码下载 git clone -b gatesgarth git://git.yoctoproject.org/poky lkmaolkmao-virtual-machine:~/yocto$ git clone -b gatesgarth git://git.yoctoproject.org/poky Cloning into poky... remote: Enumerating objects: 640690, done. remote: Counting objects: 100% (13…...

rsync+inotify-tools文件传输
目录 rsync rsync概述 rsync优缺点 rsync参数 rsync命令 rsync同步源 linux 安装rsync 安装rsync服务端 安装rsync客户端 windows 安装rsync rsync实践 inotify-tools inotify-tools概述 innotify-tools 命令、参数、事件 rsync客户端安装inotify-tools innotif…...

UGUI界面性能优化3-合理规划界面层级结构
在Unity中,UGUI(Unity GUI)是一种用于创建用户界面的工具。合理规划界面层级结构对于开发一个可维护和易于使用的界面非常重要。以下是一种合理的UGUI界面层级结构规划方式: Canvas(画布):Canva…...

《论文阅读》EmpDG:多分辨率交互式移情对话生成 COLING 2020
《论文阅读》EmpDG:多分辨率交互式移情对话生成 COLING 2020 前言简介模型架构共情生成器交互鉴别器损失函数前言 亲身阅读感受分享,细节画图解释,再也不用担心看不懂论文啦~ 无抄袭,无复制,纯手工敲击键盘~ 今天为大家带来的是《EmpDG: Multi-resolution Interactive E…...

C语言calloc函数的特点,效率低。但是进行初始化操作
#define _CRT_SECURE_NO_WARNINGS 1 #include<stdlib.h> #include<string.h> #include<errno.h> #include<stdio.h> int main() { int *p (int *)calloc(10,sizeof(int)); //初始化,效率低,然而malloc函数相反…...
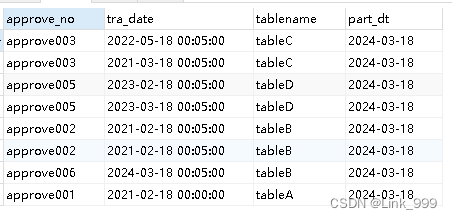
项目中遇到的sql问题记录
有一张表,表结构及数据如下: INSERT INTO test.test_approve(approve_no, tra_date, tablename, part_dt) VALUES (approve001, 2021-02-18 00:00:00, tableA, 2024-03-18); INSERT INTO test.test_approve(approve_no, tra_date, tablename, part_dt) …...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...