位图/布隆过滤器/海量数据处理方式
位图
位图的概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
直接来看问题:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在
这40亿个数中。
思路:解决问题的方法,可以使用位图来解决。把这40亿个数据映射在位图上,将位图上对应的比特位置为1。然后拿着需要判断的数在位图上看看其对应的比特位是否为1,如果是则存在,否则为0。
具体做法:
使用直接定址法,这40亿个数据的值是几,就把第几个比特位标记为1。因为40亿个整数,大概需要16G内存,而使用比特位,我们只需使用char作为存储在vector上的类型,每一个都是1bit大,因此在vector上开辟2^32大小的空间,表示数据大小范围,一共512M。

开辟好空间后,开始将每一个数据映射到位图上。每一个char对象为8bit,于是让每一个值先确定自己在哪个char对象上,然后确定映射在哪个比特位上。
x映射的值,在第 x/8 个char对象上。
x映射的值,在第 x%8 个比特位上。
所以,我们可以根据上面的理论,用代码简单实现位图
使用非模板参数N,作为数据的个数。
开辟空间:空间开辟的大小为N /8 +1,因为N个数据,每8个为一组,多开辟一组,避免N不是8的整除。然后初始化为0。即位图上的比特位一开始全是0.
//初始化空间,初始值为0bitset(){_bits.resize((N >> 3) + 1, 0);}数据映射位图上的比特位:先计算好数据所在的组别和比特位的位置,然后将其置为1。置为1的操作是让这一个char对象组别的比特位与这个数据的比特位进行或运算。
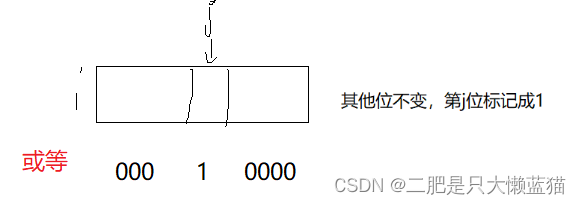
void set(size_t x){size_t i = x >> 3;//位于哪一个char对象上size_t j = x % 8;//位于这个char对象上的哪个比特位上_bits[i] |= (1 << j);//通过或运算,将x对应的比特位变为1}将某个数据映射的比特位从1变回0:同样的找到这个位置后,然后这一组别的比特位与这个数据的比特取反后进行与运算。
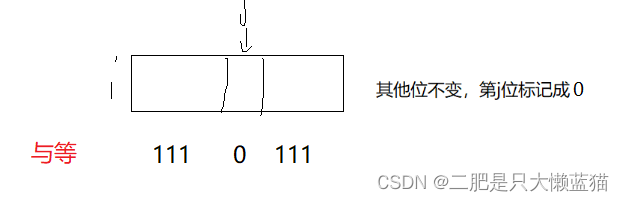
void reset(size_t x){size_t i = x >> 3;size_t j = x % 8;_bits[i] & = (~(1 << j));//通过与运算,让x对应的比特位变为0}判断一共数据是是否存在:同样,先计算出这个数据映射的位置。然后返回这一组别跟这个数据的比特,然后进行与运算,注意不是与等,是不能改变原本位图的比特位的。
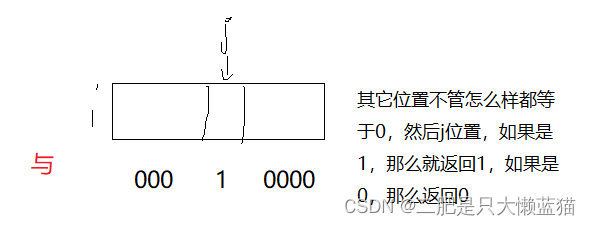
//判断x是否存在,如果存在返回truebool test(size_t x){size_t i = x >> 3;size_t j = x % 8;return _bits[i] & (1 << j);}完整代码如下:
namespace my_BitSet
{template<size_t N>class bitset{public://初始化空间,初始值为0bitset(){_bits.resize((N >> 3) + 1, 0);}void set(size_t x){size_t i = x >> 3;//位于哪一个char对象上size_t j = x % 8;//位于这个char对象上的哪个比特位上_bits[i] |= (1 << j);//通过或运算,将x对应的比特位变为1}void reset(size_t x){size_t i = x >> 3;size_t j = x % 8;_bits[i] & = (~(1 << j));//通过与运算,让x对应的比特位变为0}//判断x是否存在,如果存在返回truebool test(size_t x){size_t i = x >> 3;size_t j = x % 8;return _bits[i] & (1 << j);}private:vector<char> _bits;};
}布隆过滤器
位图对于判断大量数据中是否存在某一个数据的情况固然是好,其优点是节省空间和判断速度块。但其缺点是一般要求范围相对集中,如果范围特别分散,那么空间消耗就大了,而且是只针对整型。因此,布隆过滤器降临!
布隆过滤器的概念
布隆过滤器是一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中,因为布隆过滤器是哈希+位图的结合。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
一般的位图下,每一个数据只跟位图产生一个映射点,而且只能用于整型。但布隆过滤器是每一个数据可以有N个映射点,N个映射点对应于N个哈希函数,这个是我们自己定义的。用哈希函数将非整型转化成整型。
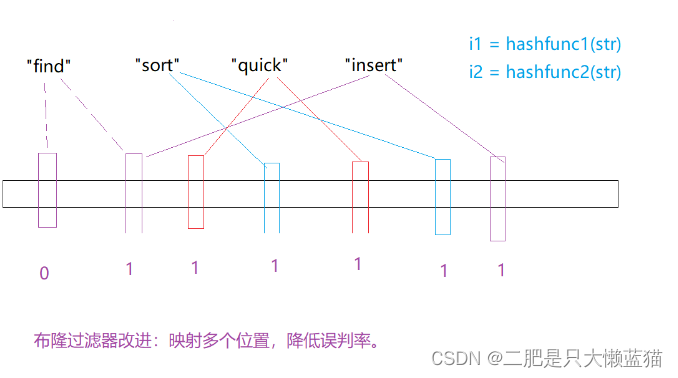
布隆过滤器的长度的计算方式:
使用公式:
K为哈希函数的个数,m为布隆过滤器长度,n为数据的个数。假设K为3,而ln2约等于0.7,因此m==4.2n。
布隆过滤器的功能支持:
布隆过滤器支持set和test方法,最好不要有将1变回0的操作。因为这样会导致其它数据的判断的误差。如果真的要支持,就用计数的方法,但这种方法不推荐。
简单实现代码如下
这里使用3个哈希函数,分别为:BKDRHash、APHash和DJBHash。使用string为类型。
set方法:
void set(const K& key){//通过不同的哈希函数,让同一个数据可以计算出三个不同的位置size_t hash1 = HashFunc1()(key) % (N * X);size_t hash2 = HashFunc2()(key) % (N * X);size_t hash3 = HashFunc3()(key) % (N * X);//计算出位置后,使用位图的set方法将位图上对应的比特位进行0变1_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}test方法:
bool test(cost K& key){//先逐个位置判断,如果它是0,直接返回falsesize_t hash1 = HashFunc1()(key) % (N * X);if (!_bs.test(hash1)){return false;}size_t hash2 = HashFunc2()(key) % (N * X);if (!_bs.test(hash2)){return false;}size_t hash3 = HashFunc3()(key) % (N * X);if (!_bs.test(hash3)){return false;}//直到最后,说明该数据是存在的,返回truereturn true;}整体代码如下:
namespace my_BloomFilter
{struct BKDRHash{size_t operator()(const string& key){size_t hash = 0;for (auto ch : key){hash *= 131;hash += ch;}return hash;}};struct APHash{size_t operator()(const string& key){unsigned int hash = 0;int i = 0;for (auto ch : key){if ((i & 1) == 0){hash ^= ((hash << 7) ^ (ch) ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ (ch) ^ (hash >> 5)));}++i;}return hash;}};struct DJBHash{size_t operator()(const string& key){unsigned int hash = 5381;for (auto ch : key){hash += (hash << 5) + ch;}return hash;}};template<size_t N,size_t X = 5,class K = string,class HashFunc1 = BKDRHash,class HashFunc2 = APHash,class HashFunc3 = DJBHash>class BloomFilter{public:void set(const K& key){//通过不同的哈希函数,让同一个数据可以计算出三个不同的位置size_t hash1 = HashFunc1()(key) % (N * X);size_t hash2 = HashFunc2()(key) % (N * X);size_t hash3 = HashFunc3()(key) % (N * X);//计算出位置后,使用位图的set方法将位图上对应的比特位进行0变1_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}bool test(cost K& key){//先逐个位置判断,如果它是0,直接返回falsesize_t hash1 = HashFunc1()(key) % (N * X);if (!_bs.test(hash1)){return false;}size_t hash2 = HashFunc2()(key) % (N * X);if (!_bs.test(hash2)){return false;}size_t hash3 = HashFunc3()(key) % (N * X);if (!_bs.test(hash3)){return false;}//直到最后,说明该数据是存在的,返回truereturn true;}private:std::bitset<N* X> _bs;};
}
海量数据处理问题
哈希切割
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?
超过100G大小的文件,肯定不能直接放到内存中,而是通过将它切割,分成很多份。那么如何去切割呢?是平均分成100份,每一份1G这样吗?
如果平均切割,那么会导致的问题是:如果文件中有好几个相同的值,且分布不集中,此时平均切割就很可能使一个IP有很多份在很多小文件中。
因此不能平均切割,需要的是哈希切割。哈希切割就是通过取模,让取模结果相同的数据放到同一份小文件里面。
哈希切割后,通过map来对每一个小文件进行统计。

小问题如果超过1G的问题:
①不重复的IP有很多个,map就需要很多节点,因此map是统计不下来的。
②重复的IP有很多个,map可以统计下来,因为节点不多。
解决方法:
先不看什么情况,直接用map统计,如果是第二种情况的话就直接统计下来了。但是第一种情况,会在insert的时候失败,因此可以在失败的时候捕捉异常,接着换哈希函数递归切分再统计即可。
位图的应用
1.给定100亿个整数,设计算法找到只出现一次的整数?
只出现一次,那就说明,它在位图中比特位是:01。如果找到该位置发现是00或11或者其它的情况,那就不是。
但一个一般的位图只会出现单个比特,即要么是0,要么是1,不会出现两个比特。这里的方法使用两个位图的结构。即定义两个位图,然后用同一个数据计算出来的同一个位置,分别在这个两个位图上进行0和1的操作。

简单的代码实现:
template<size_t N>class twobitset{public:void set(size_t x){//初次映射:两个位图对应的比特位都为0,即00if (!_bs1.test(x) && !_bs2.test(x)// 00{_bs2.set(x);// 01}else if (!_bs1.test(x) && _bs2.test(x) // 01{//第二次遇到这个数字后,此时是01的,要变成10_bs1.set(x); //11_bs2.reset(x); // 10}//如果第三次遇到,也不用管了,第二次遇到的时候就已经不是它了//10//11}void PrintOnce(){for (size_t i = 0; i < N; ++i){if (!_bs1.test(i) && _bs2.test(i)) // 01 出现一次{cout << i << endl;}}cout << endl;}private:bitset<N> _bs1;bitset<N> _bs2;};
}2.给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
这里提供两种思路:
思路1:先将一个文件的数据映射到位图中,然后用另外一个文件的数据去遍历,得到交集,需要注意去重。
思路2:分布将两文件映射到两个位图,然后通过两位图的与运算判断是否有交集。
3.位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数。
这道问题跟第一个问题基本一样,就是让“01”和"10"为需要找到的整数。如果出现"11"以上,那么就不行。
布隆过滤器的应用
1. 给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法。
query是一般为一个查询指令,可能是一个网络请求的指令,也可能是一个数据库sql语句。
精确算法找文件交集的思路是:分别给两个文件创建布隆过滤器,然后让它们进行哈希切割,分成一个个小文件。最后通过编号相同的小文件中查找交集。
近似算法的思路是:将一个文件的数据映射到一个布隆过滤器中,然后另外一个文件去查找有没有相同的,有就是交集。这种算法会造成误判。
相关文章:

位图/布隆过滤器/海量数据处理方式
位图 位图的概念 所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。 直接来看问题: 给40亿个不重复的无符号整数,没排过序。给一个无符号整数࿰…...
Tomcat 配置文件数据库密码加密
几年前研究过Tomcat context.xml 中数据库密码改为密文的内容,因为当时在客户云桌面代码没有留备份也没有文章记录,最近项目又提出了这个需求就又重新拾起来学习一下。在网上找了一些资料,自己也大概试了一下,目前功能是实现了。参…...
k8s-Kubernetes集群部署
文章目录前言一、Kubernetes简介与架构1.Kubernetes简介2.kubernetes设计架构二、Kubernetes集群部署1.集群环境初始化2.所有节点安装kubeadm3.拉取集群所需镜像3.集群初始化4.安装flannel网络插件5.扩容节点6.设置kubectl命令补齐前言 一、Kubernetes简介与架构 1.Kubernetes…...

Python数据分析案例19——上市银行财务指标对比
我代码栏目都是针对基础的python数据分析人群,比如想写个本科毕业论文,课程论文,做个简单的案例分析等。过去写的案例可能使用了过多的机器学习和深度学习方法,文科的同学看不懂,可能他们仅仅只想用python做个回归或者…...

Python 中错误 ConnectionError: Max retries exceeded with url
出现错误“ConnectionError: Max retries exceeded with url”有多种原因: 向 request.get() 方法传递了不正确或不完整的 URL。我们正受到 API 的速率限制。requests 无法验证您向其发出请求的网站的 SSL 证书。 确保我们指定了正确且完整的 URL 和路径。 # ⛔️…...

SpringBoot下的Spring框架学习(Tedu)——DAY02
SpringBoot下的Spring框架学习(Tedu)——DAY02 目录SpringBoot下的Spring框架学习(Tedu)——DAY02Spring框架学习1.1 Spring介绍1.2 知识铺垫1.2.1 编辑Dog类1.2.2 编辑Cat类1.2.3 编辑测试类User.java1.2.4 上述代码的总结1.3 面…...

容易混淆的点:C语言中char* a[] 与 char a[] 的区别以及各自的用法
char* a[] 和 char a[] 的区别 char* a[] 和 char a[] 是 C 语言中数组的不同声明方式,二者具有以下区别: char a[] 声明的是一个字符数组,其中存储的是一串字符。此时,a 可以被视为一个指向字符的指针。 char* a[]则声明了一个…...
认识Spring(下)
作者:~小明学编程 文章专栏:Spring框架 格言:热爱编程的,终将被编程所厚爱。 目录 Spring更加高效的读取和存储对象 存储bean对象 五大注解 关于五大类注解 对象的注入 属性注入 构造方法注入 Setter注入 三种注入方式的…...
 C - Maximum Set)
Educational Codeforces Round 144 (Rated for Div. 2) C - Maximum Set
传送门 题意: 对于一个集合,如果它的任意两个元素都能 有 其中一个能整除另一个,那么它是好的。问在区间[L,R] 中由这个区间某些数内构成的好的集合的最长长度是多少,以及且满足这个长度的好集合有多少个。(懒得想就借…...
学python的第四天---基础(2)
一、三角形类型读入数组并排序的方法nlist(map(float,input().split())) c,b,asorted(n)list_1 list(map(float, input().split())) list_1.sort() list_1.reverse()lengthssorted(map(float,input().split(" ")),reverseTrue)二、动物写法一:d{" &…...
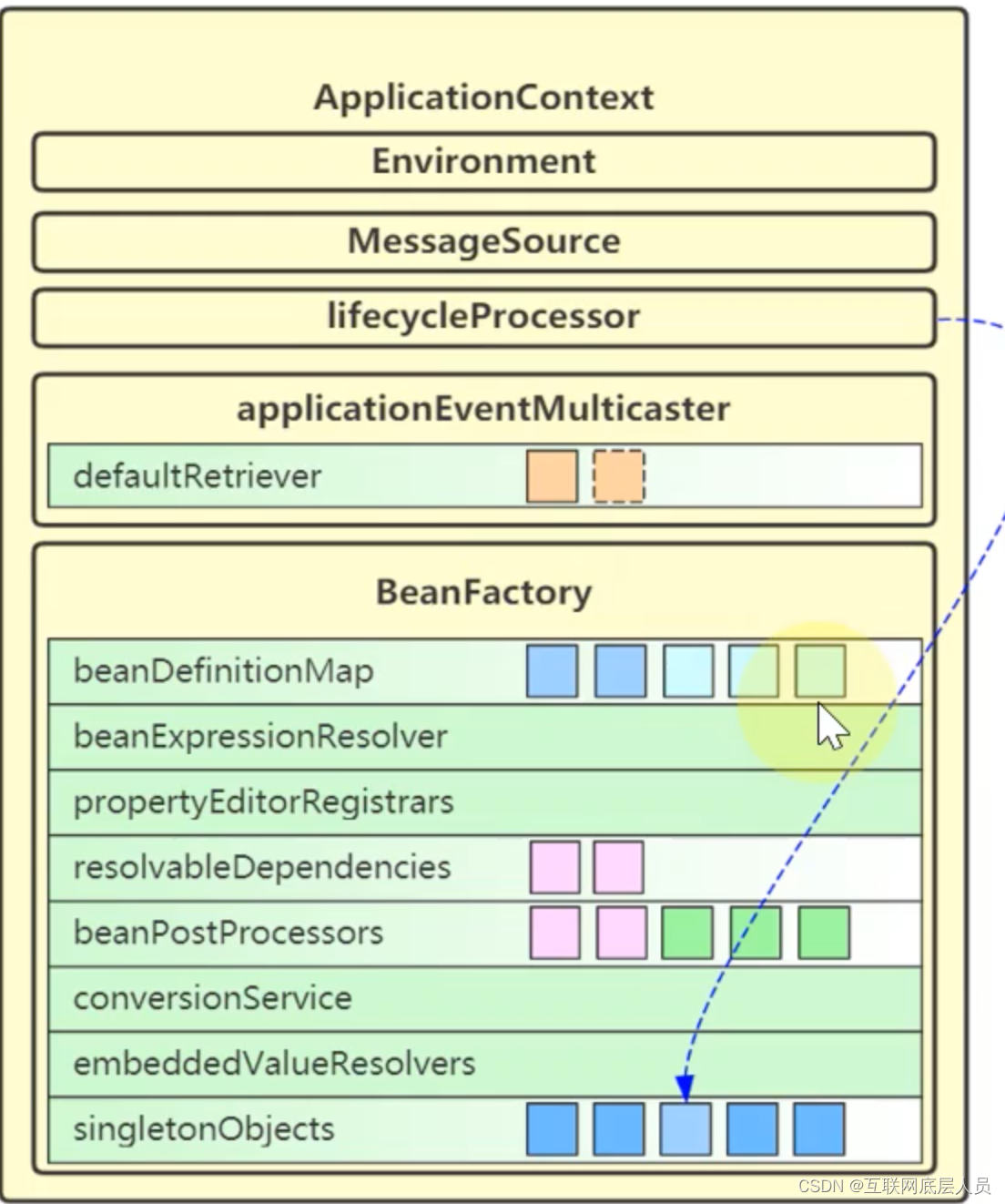
spring之refresh流程-Java八股面试(六)
系列文章目录 第一章 ArrayList-Java八股面试(一) 第二章 HashMap-Java八股面试(二) 第三章 单例模式-Java八股面试(三) 第四章 线程池和Volatile关键字-Java八股面试(四) 第五章ConcurrentHashMap-Java八股面试(五) 动态每日更新算法题,想要学习的可以关注一下…...
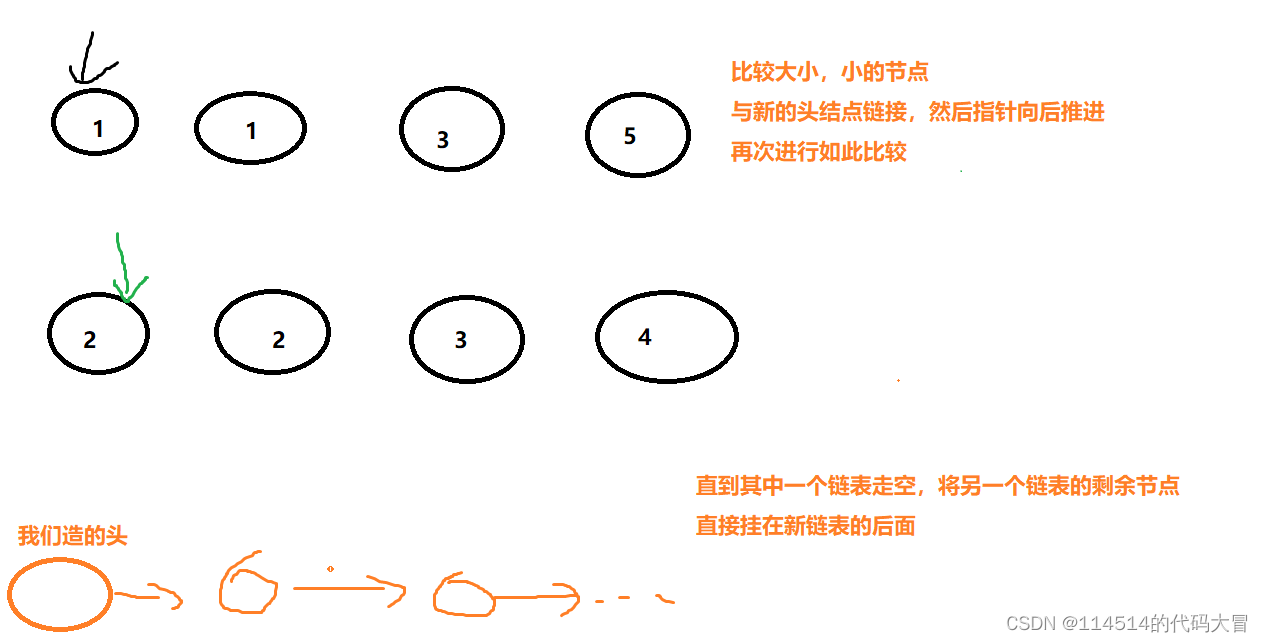
【C语言】刷题|链表|双指针|指针|多指针|数据结构
主页:114514的代码大冒 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 文章目录 目录 文章目录 前言 一、移除链表元素 二、反转链表 三,链表的中间结点 四&…...

糖化学类854262-01-4,Propargyl α-D-Mannopyranoside,炔丙基 α-D-吡喃甘露糖苷
外观以及性质:Propargyl α-D-Mannopyranoside一般为白色粉末状,糖化学类产品比较多,一般包括:葡萄糖衍生物、葡萄糖醛酸衍生物,氨基甘露糖衍生物、半乳糖衍生物、氨基半乳糖衍生物、核糖衍生物、阿拉伯糖衍生物、唾液…...
项目管理工具DHTMLX 在 G2 排名中再创新高
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的大部分开发需求,具备完善的甘特图图表库,功能强大,价格便宜,提供丰富而灵活的JavaScript API接口,与各种服务器端技术&am…...

28 位委员出席,龙蜥社区第 15 次运营委员会会议顺利召开
2 月 24 日,龙蜥社区在海光召开了第 15 次运营委员会会议,本次会议由统信软件运营委员会委员崔开主持。来自 Arm、阿里云、飞腾、红旗软件、海光、Intel、龙芯、联通软研院、浪潮信息、普华基础软件、统信软件、万里红、移动、中科方德等理事单位的 28 位…...
自然语言处理-基于预训练模型的方法-chapter3基础工具集与常用数据集
文章目录3.1NLTK工具集3.1.1常用语料库和词典资源3.1.2常见自然语言处理工具集3.2LTP工具集3.3pytorch基础3.3.1张量基本概念3.3.2张量基本运算3.3.3自动微分3.3.4调整张量形状3.3.5广播机制3.3.6索引与切片3.3.7降维与升维3.4大规模预训练模型3.1NLTK工具集 3.1.1常用语料库和…...

【SpringMVC】@RequestMapping
RequestMapping注解 1、RequestMapping注解的功能 从注解名称上我们可以看到,RequestMapping注解的作用就是将请求和处理请求的控制器方法关联起来,建立映射关系。 SpringMVC 接收到指定的请求,就会来找到在映射关系中对应的控制器方法来处…...
【深度学习】BERT变体—SpanBERT
SpanBERT出自Facebook,就是在BERT的基础上,针对预测spans of text的任务,在预训练阶段做了特定的优化,它可以用于span-based pretraining。这里的Span翻译为“片段”,表示一片连续的单词。SpanBERT最常用于需要预测文本…...
)
根据身高体重计算某个人的BMI值--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例3:根据身高体重计算某个人的BMI值 BMI又称为身体质量指数,它是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准。我国制定的BMI的分类标准如表1所示。 表1 BMI的分类 BMI 分类 <18.5 过轻 18.5 < BMI < 23.9 正常 24 < BM…...

高并发编程JUC之进程与线程高并发编程JUC之进程与线程
1.准备 pom.xml 依赖如下: <properties><project.build.sourceEncoding>UTF-8</project.build.sourceEncoding><maven.compiler.source>1.8</maven.compiler.source><maven.compiler.target>1.8</maven.compiler.target&g…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
