数据的标准化处理
假设各个指标之间的水平相差很大,此时直接使用原始指标进行分析时,数值较大的指标,在评价模型中的绝对作用就会显得较为突出和重要,而数值较小的指标,其作用则可能就会显得微不足道。
因此,为了统一比较的标准,保证结果的可靠性,我们在分析数据之前,需要对原始变量进行一定的处理,即我们本期内容将向大家介绍的数据的标准化处理,将原始数据转化为无量纲、无数量级差异的标准化数值,消除不同指标之间因属性不同而带来的影响,从而使结果更具有可比性。
数据的标准化
数据的标准化,是通过一定的数学变换方式,将原始数据按照一定的比例进行转换,使之落入到一个小的特定区间内,例如0~1或-1~1的区间内,消除不同变量之间性质、量纲、数量级等特征属性的差异,将其转化为一个无量纲的相对数值,也就是标准化数值,使各指标的数值都处于同一个数量级别上,从而便于不同单位或数量级的指标能够进行综合分析和比较。
数据标准化处理的类型
数据标准化处理主要包括指标一致化处理和无量纲化处理两种类型。
一、指标一致化处理
指标一致化处理,主要解决的是数据之间不同性质的问题。例如我们在评价多个不同指标的作用时,某一类指标,数值越大越好,我们称之为正指标,例如诊断符合率、病床平均周转次数等指标;
另有一类指标,数值越小越好,我们称之为逆指标,例如平均住院日、围产期婴儿死亡率等指标。
在这种情况下,如果同时评价这两类指标的综合作用,由于他们的作用方向不同,将不同性质的指标作用直接相加,并不能正确反映不同作用方向产生的综合结果,此时我们就需要对逆指标进行一致化处理,改变逆指标的性质和作用方向,使所有指标作用方向一致化,从而得出适宜的结果。
针对逆指标一致化处理的方法主要有两种:
1、倒数一致化,即对原始数据取倒数,X’ = 1 / x(x>0)
2、减法一致化,即利用该指标允许范围内的一个上界值(M),依次减去每一个原始数据,X’ = M - x
注意:倒数一致化常常会改变原始数据的分散程度,这种改变会夸大或缩小原始数据的实际差异,对于进行综合评价是不利的。而减法一致化则不改变数据的分散程度,因此结果较倒数一致化而言会更加稳定。
二、无量纲化处理
数据无量纲化处理,主要解决数据之间可比性的问题,这也是我们对数据进行标准化处理的最主要的一个目的。
在实际的应用中,由于不同变量自身的量纲不同,数量级存在较大差异,在进行综合评价时,不同变量所占的作用比重也会有所不同。例如,某个变量的数值在1-10之间,而另一个变量的数值范围在100-1000之间,此时若进行综合评价,从数值的角度,很有可能数值变化范围大的变量,它的绝对作用就会较大,所占的比重较大。
因此,为了消除量纲、变量自身变异和数值大小的影响,比较不同变量之间的相对作用,就需要对数据进行无量纲化处理,将其转化为无量纲的纯数值来进行评价和比较。
常用的数据标准化方法
一、极差标准化法
极差标准化法,是消除变量量纲和变异范围影响最简单的方法。
具体的操作方法为:首先需要找出该指标的最大值(Xmax)和最小值(Xmin),并计算极差(R = Xmax - Xmin),然后用该变量的每一个观察值(X)减去最小值(Xmin),再除以极差(R),即:
X’ = (X-Xmin) / (Xmax-Xmin)
经过极差标准化方法处理后,无论原始数据是正值还是负值,该变量各个观察值的数值变化范围都满足0≤X’≤1,并且正指标、逆指标均可转化为正向指标,作用方向一致。但是如果有新数据加入,就可能会导致最大值(Xmax)和最小值(Xmin)发生变化,就需要进行重新定义,并重新计算极差(R)。
二、Z-score标准化法
当我们遇到某个指标的最大值和最小值未知的情况时,或者有超出取值范围的离群数值的时候,就不再适宜计算极差了,此时我们可以采用另一种数据标准化最常用的方法,即Z-score标准化,也叫标准差标准化法。
具体的操作方法为:

经过Z-score标准化后,数据将符合标准正态分布,即将有约一半观察值的数值小于0,另一半观察值的数值大于0,变量的均值为0,标准差为1,变化范围为-1≤X’≤1。
三、线性比例标准化法
1、极大化法
对于正指标,取该指标的最大值Xmax,然后用该变量的每一个观察值除以最大值,即:X’=X / Xmax。(X≥0)
2、极小化法
对于逆指标,取该指标的最小值Xmin,然后用该变量的最小值除以每一个观察值,即:X’ = Xmin / X。(X>0)
注意,以上两种方法不适用于X<0的情况。对于逆向指标使用线性比例法进行标准化后,实际上是进行了非线性的变换,变换后的指标无法客观地反映原始指标的相互关系,转换时需要注意。
四、log函数标准化法
首先对该变量的每一个观察值取以10为底的log值,然后再除以该指标最大值(Xmax)的log值,即:
X’=log10X / log10 Xmax
注意,此方法要求X≥1。
五、反正切函数标准化法
通过三角函数中的反正切函数(arctan)也可以实现数据的标准化转换,计算方法如下:
X’ = arctan(X)*2 / π
注意,如果原始数据为正、负实数,则标准化后的数据区间为-1≤X’≤1,若要得到0≤X’≤1区间,则原始数据应该保证X≥0。
当然,数据标准化的处理还有其他方法,最常用的还是前两种:极差标准化法和Z-score标准化法。
相关文章:

数据的标准化处理
假设各个指标之间的水平相差很大,此时直接使用原始指标进行分析时,数值较大的指标,在评价模型中的绝对作用就会显得较为突出和重要,而数值较小的指标,其作用则可能就会显得微不足道。 因此,为了统一比较的标…...

性能优化|记一次线上OOM问题处理
概述最近线上监控发现 OOM 涨幅较大,因此去尝试定位和修复这个问题,在修复了一些内存泄漏和大对象占用问题后, OOM 依旧未达到正常标准,在这些新上报的 hprof 文件中,发现几乎所有 case 中都有个叫 FinalizerReference 的对象&…...

Vue动态粒子特效插件(背景线条吸附动画)
目录 效果图: 一、安装: 二、引入 main.js 文件: 三、使用: 四、属性说明: 效果图: 一、安装: npm install vue-particles --save 二、引入 main.js 文件: import VueParticles…...

【Java 类】002-类、属性、方法、代码块
【Java 类】002-类、属性、方法、代码块 文章目录【Java 类】002-类、属性、方法、代码块一、类1、类与对象2、类的作用3、创建与使用类类结构创建类调用类运行结果4、Java 类的执行过程5、封装、继承、多态、抽象类、内部类、接口、枚举、记录、注解等二、属性1、概述2、类型3…...

Ubuntu Linux 编译安装的基本步骤
文章目录1 基本步骤若报错: No such file or directory2 解压 tar.bz2文件参考:1 基本步骤 解压: tar -zxvf file.tar.gz 进入解压后的文件夹: cd file 源码编译安装 ./configure # ./configmakesudo make install 若报错&…...
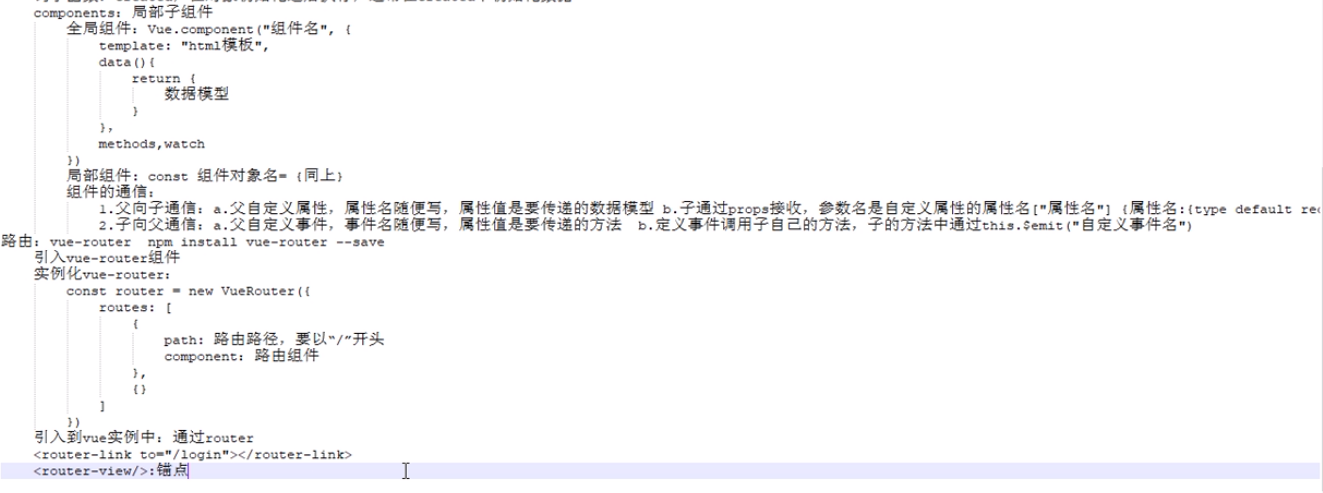
day59反刍笔记
1.本地环境安装vue后,没有vue.js文件,只有vue.cjs.js文件, 引用后也无法正常使用,看npm install vue后的文件夹中没有vue.js文件_找不到vue.js_一枝风的博客-CSDN博客 老哥的博客后得到启发,将原本的命令由࿱…...

【阅读笔记】你不知道的Javascript--强制类型转换4
目录强制类型转换基本概念JSONboolean强转归纳其他知识点被诟病的安全使用隐式强转法则抽象关系比较语法表达式变动强制类型转换 基本概念 类型转换发生在静态类型语言的编译阶段; 强制类型转换则发生在动态类型语言的运行时(runtime) JSON…...
)
华为OD机试真题Python实现【有效子字符串】真题+解题思路+代码(20222023)
有效子字符串 题目 输入两个字符串S和L,都只包含小写字母, S长度 <= 100,L长度 <= 500000, 判断S是否是L的有效子字符串, 判定规则:S中的每个字符在L中都能找到(可以不连续) 且S在L中字符的前后顺序与S中顺序要保持一致 例如: S="ace"是L="abcd…...
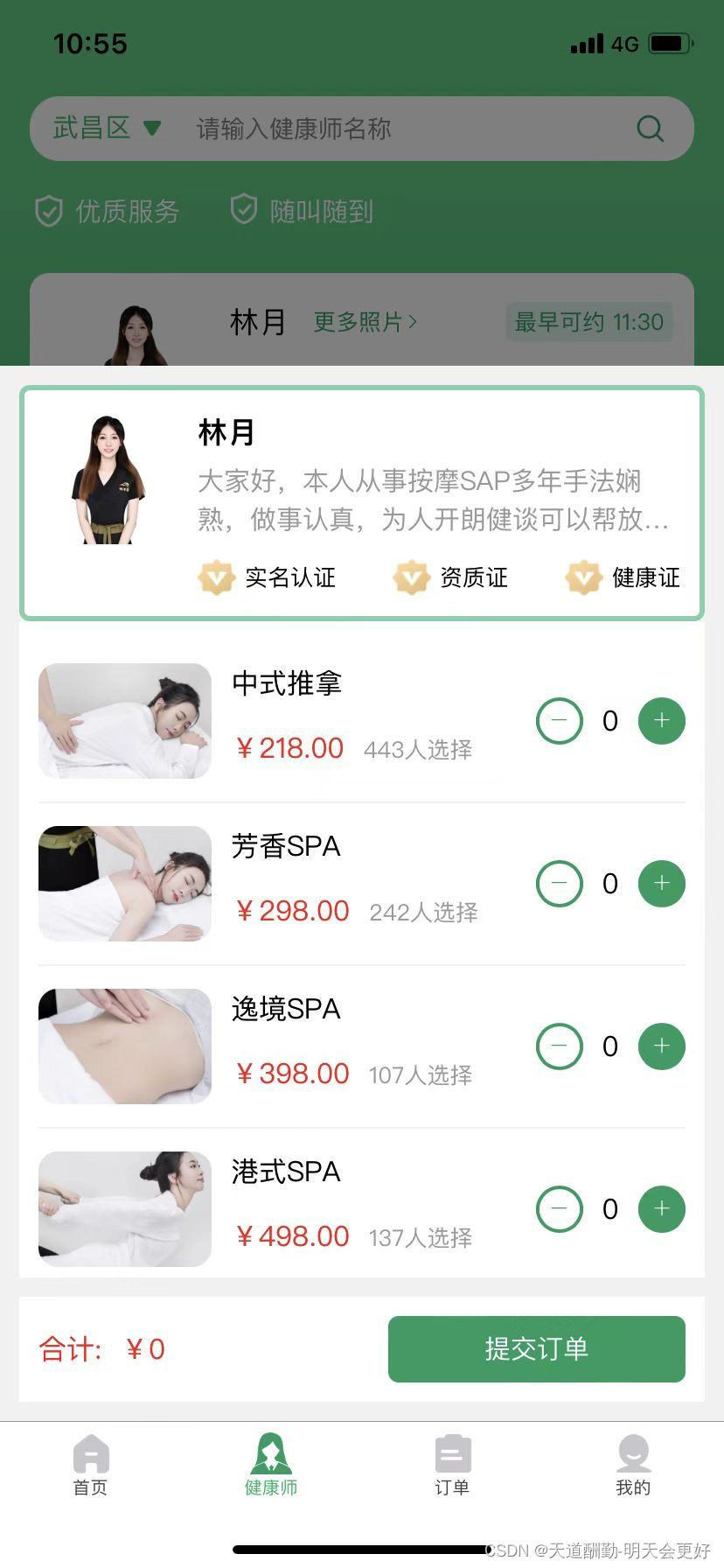
上门按摩预约APP源码-东郊到家源码(开发,PHP,平台搭建)
一、什么是上门按摩预约APP源码? 上门按摩预约APP源码是一款家政服务类型的APP,可以帮忙用户在家就能享受按摩的服务。APP源码分两端,一端是用户端,另外一端是技师端。采用的技术,前端是安卓IOS,后端是PHP&…...
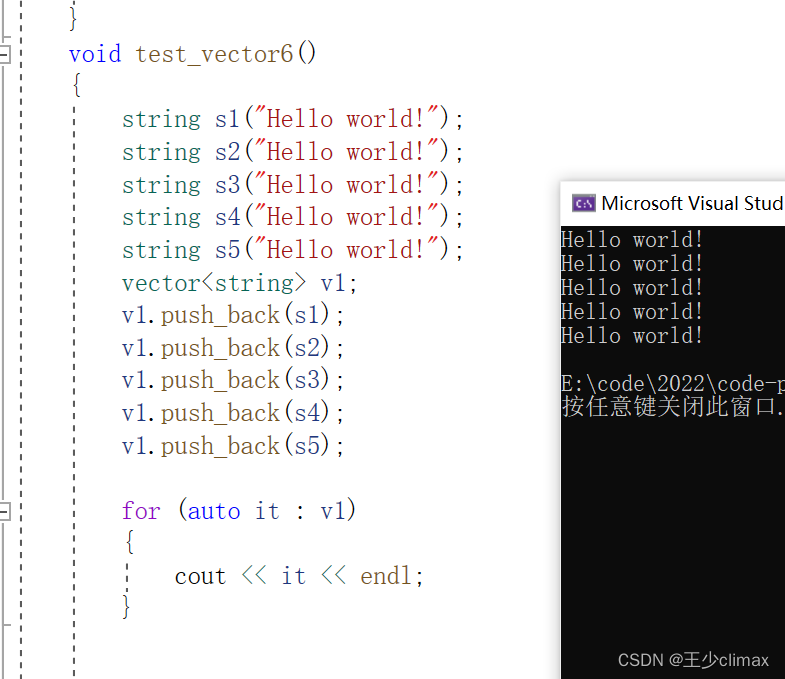
STL讲解——模拟实现vector
STL讲解——模拟实现vector vector深度剖析 在STL源码中,发现vector定义的并不是 start、size、capacity,而是start、finish、end_of_storage. 这样就可以得到size()和capacity()。 sizefinish-start capacityend_of_storage-start 扩容可能是本地扩容也…...

各种经典排序算法介绍及实现源码
一,冒泡排序(Bubble Sort) 排序算法是程序员必须了解和熟悉的一类算法,排序算法有很多种,基础的如:冒泡、插入、选择、快速、归并、计数、基数和桶排序等。 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求,如果不…...

历史大讲堂:这是真·图形化 苹果系统历史回顾(上)
众所周知,米国有个非常牛掰的公司叫苹果,想必大家对这个logo不陌生吧。 目前已发布的苹果产品有iPhone、iPad、iPod等等,简直花样繁多,而且各种功能很好用,我的手机就是一部苹果iPhone X。 等一下,似乎扯远…...
今天女神节,用python画个贺卡送给母亲吧
今天女神节,你给女神妈妈准备了什么祝福呢?如果还没有,那么画个贺卡送给她吧,在你眼里,她是一个什么样的人呢? 是"可爱",“温柔”,“美丽”,“漂亮”…...
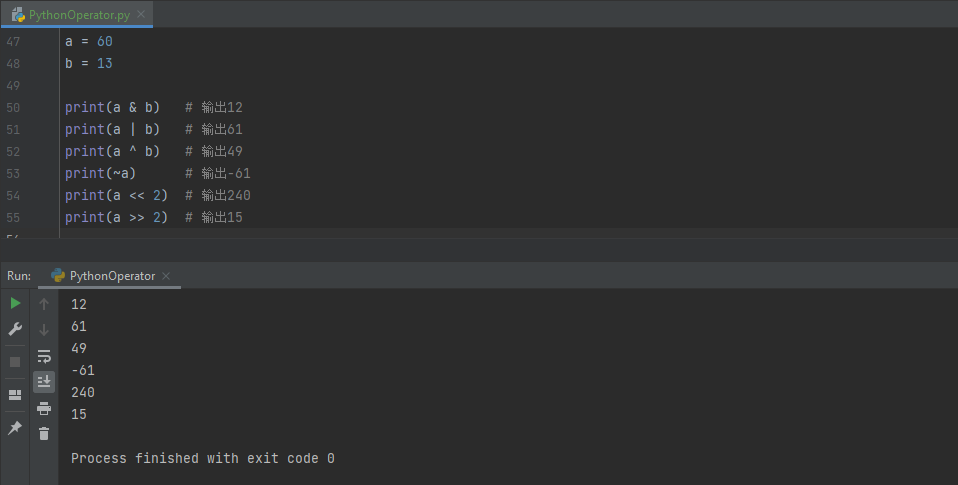
【编程基础之Python】11、Python中的表达式
【编程基础之Python】11、Python中的表达式Python中的表达式表达式与运算符算术表达式赋值表达式比较表达式逻辑表达式位运算表达式总结Python中的表达式 在Python中,表达式是由操作数、运算符和函数调用等组成的语法结构,可以进行各种数学运算、逻辑判…...
)
华为OD机试真题Python实现【乱序整数序列两数之和绝对值最小】真题+解题思路+代码(20222023)
乱序整数序列两数之和绝对值最小 题目 给定一个随机的整数数组(可能存在正整数和负整数)nums, 请你在该数组中找出两个数,其和的绝对值(|nums[x]+nums[y]|)为最小值 并返回这两个数(按从小到大返回)以及绝对值。 每种输入只会对应一个答案。但是,数组中同一个元素不能使用两…...
(python))
字符串转换整数 (atoi)(python)
链接: https://leetcode.cn/problems/string-to-integer-atoi 题目描述: 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C 中的 atoi 函数)。 函数 myAtoi(string s) 的算法…...

洛谷 P1115 最大子段和
题目链接:P1115 最大子段和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述 给出一个长度为 n 的序列 a,选出其中连续且非空的一段使得这段和最大。 输入格式 第一行是一个整数,表示序列的长度 n。 第二行有 n 个整数ÿ…...
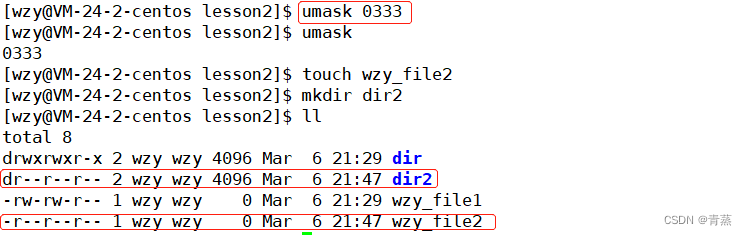
【Linux】-- 权限和Shell运行原理
目录 Shell的运行原理 用户切换 su - / su sudo 权限 chmod chown chgrp 八进制方法修改文件属性 目录权限 粘滞位 umask 自定义默认权限 Shell的运行原理 广义上,Linux发行版 Linux内核 外壳程序 Linux 从广义上来理解它是一个操作系统 而从狭义上…...
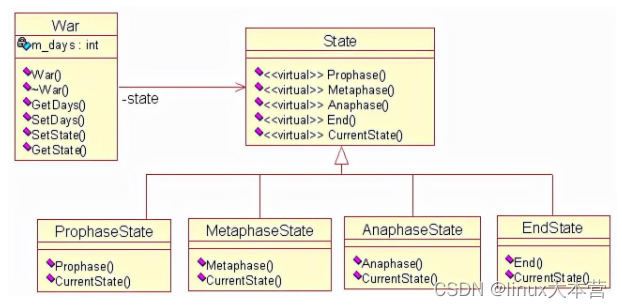
C++各类设计模式及实现详解
软件领域中的设计模式为开发人员提供了一种使用专家设计经验的有效途径。设计模式中运用了面向对象编程语言的重要特性:封装、继承、多态,真正领悟设计模式的精髓是可能一个漫长的过程,需要大量实践经验的积累。最近看设计模式的书࿰…...
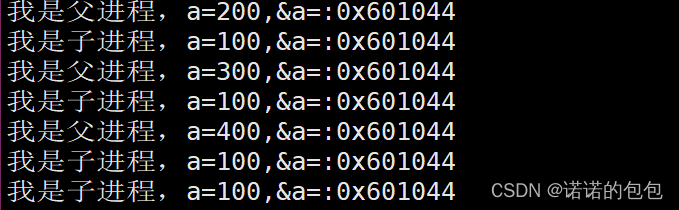
【Linux】进程理解与学习(Ⅰ)
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹相关文章推荐:【Linux】冯.诺依曼体系结构与操作系统进程概念什么是进程?进程是什么?我们打开任务管理器可以看到有…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
