C语言 青蛙跳台阶问题
目录
编辑
1.问题描述
2.问题分析
3.全部代码
4.结语
1.问题描述
一只青蛙可以一次跳一级台阶,也可以一次跳两级台阶,如果青蛙要跳上n级台阶有多少种跳法?
2.问题分析
当台阶只有一级时,只能跳一级,所以只有一种跳法
当台阶有两级时,可以先跳一级,再跳一级,或者直接跳两级
所以有两种跳法
当台阶有三级时,可以这么来思考,
假如先跳一级,剩下的就是二级台阶的情况,
如果先跳两级,那么剩下的一级,剩下的就是一级台阶的情况,
则三级台阶的跳法等于前两级台阶之和,
假如是五级台阶,可以先拆为四级和三级,再把四级和三级往下拆解即可
所以前两次台阶数量等于跳法
当台阶数量大于二时,可以看成斐波拉契数列来计算:n = (n-1) + (n-2)
3.全部代码
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>int frog(int n)
{if (n <= 2)return n;//当台阶级数小于等于2时的跳法elsereturn frog(n - 1) + frog(n - 2);//当台阶级数大于2时的跳法
}int main()
{int n = 0;scanf("%d", &n);//可以随机输入台阶的级数int m = frog(n);//创建一个frog函数printf("%d\n", m);
}4.结语
今天的经验分享就到这里,有喜欢的朋友可以点赞➕评论➕收藏➕关注,如果有不懂的地方可以咨询博主,谢谢大家支持博主!
相关文章:
C语言 青蛙跳台阶问题
目录 编辑 1.问题描述 2.问题分析 3.全部代码 4.结语 1.问题描述 一只青蛙可以一次跳一级台阶,也可以一次跳两级台阶,如果青蛙要跳上n级台阶有多少种跳法? 2.问题分析 当台阶只有一级时,只能跳一级,所以只有一…...
【Django开发】前后端分离美多商城项目第3篇:用户部分,1. 后端接口设计:【附代码文档】
美多商城项目4.0文档完整教程(附代码资料)主要内容讲述:美多商城,项目准备1.B2B–企业对企业,2.C2C–个人对个人,3.B2C–企业对个人,4.C2B–个人对企业。项目准备,配置1. 修改settings/dev.py 文件中的路径信息,2. INS…...

DHCP snooping、DHCP安全及威胁防范
DHCP snooping、DHCP安全及威胁防范 [SW1]display dhcp snooping user-bind all,查看DHCP snooping表项。 DHCP snooping: 表项是通过服务器发送给客户端的ACK报文生成的。 只能在交换机上开启,路由器不支持,并且建议在接入交…...
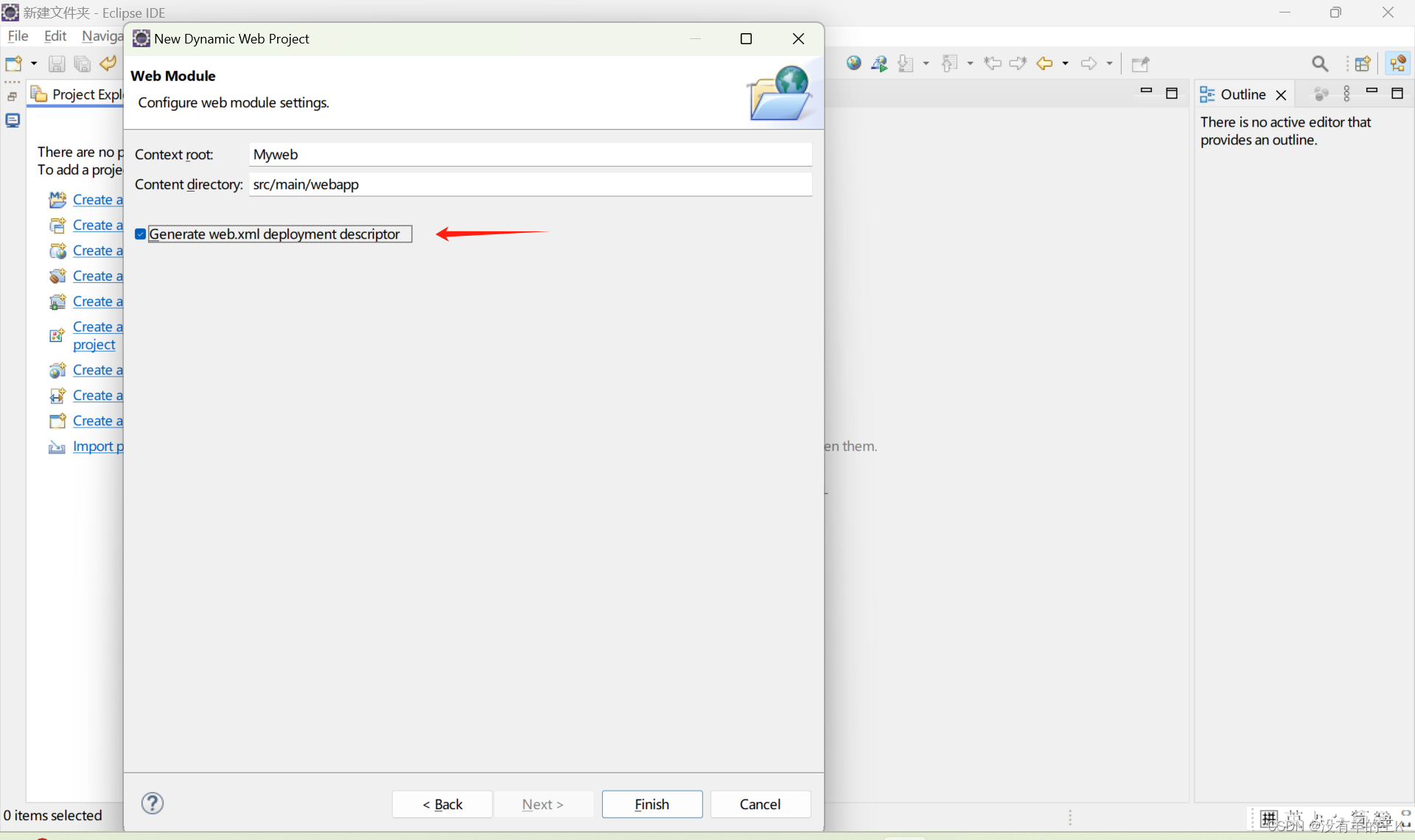
用eclipse创建Web项目,通过Servlet实现Web访问的功能。
要使用Eclipse和Tomcat 10创建一个简单的Web项目,并通过Servlet实现Web访问功能,你需要遵循以下详细步骤: 1. 安装和配置Eclipse和Tomcat 10 确保你已经安装了Eclipse IDE for Java EE Developers和Tomcat 10。如果还没有安装,请…...
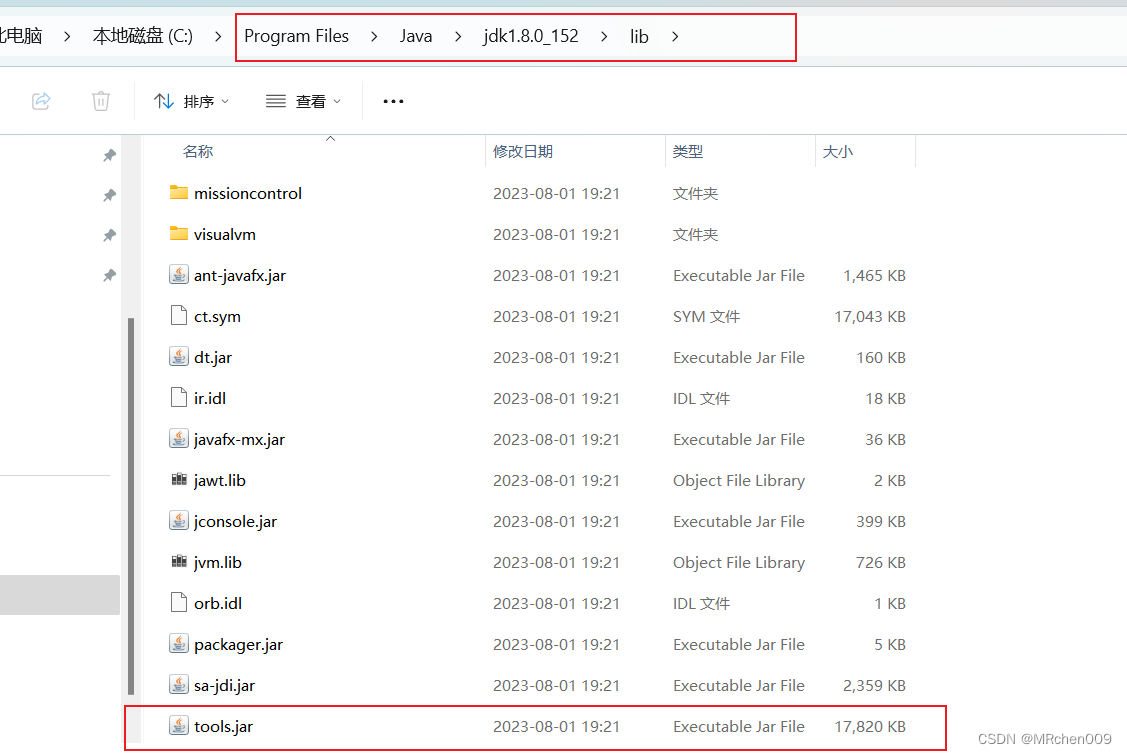
tools.jar下载 Unable to create schema compiler
网上查找了一堆下载tools.jar的都是忽悠人的,在这我就直接告诉大家,直接在电脑的JDK安装路径下的lib文件下复制就可以了。如果没有的话可以diss我我发给你...
初始化(3))
【0278】checkpointer 共享内存(CheckpointerShmem)初始化(3)
0. 关于checkpointer 检查指针是Postgres 9.2的新特性。它处理所有检查点。自上次检查点以来,检查点在经过一定时间后自动分发,并且还可以发出信号来执行请求的检查点。(GUC参数要求每隔这么多WAL段就有一个检查点,这是通过后端在填充WAL段时发出信号来实现的; checkpointer…...
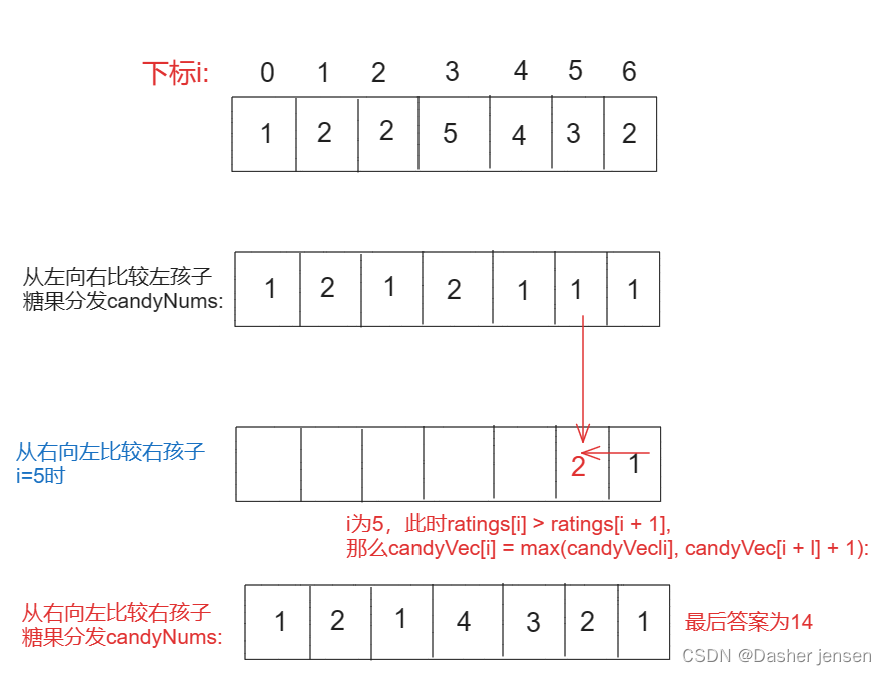
算法打卡day29|贪心算法篇03|Leetcode 1005.K次取反后最大化的数组和、134. 加油站、135. 分发糖果
算法题 Leetcode 1005.K次取反后最大化的数组和 题目链接:1005.K次取反后最大化的数组和 大佬视频讲解:K次取反后最大化的数组和视频讲解 个人思路 思路清晰,因为是取反当然是取越小的负数越好,那么先按绝对值排序。如果是负数就取反&#…...
【hexo博客6】自定义域名 购买、配置、更新部署
【hexo博客6】自定义域名 购买、配置、更新部署 写在最前面自定义域名购买域名DNS配置Github 配置 更新部署博客 🌈你好呀!我是 是Yu欸 🌌 2024每日百字篆刻时光,感谢你的陪伴与支持 ~ 🚀 欢迎一起踏上探险之旅&#…...

Django使用pyJwt进行token校验
1.登录成功后返回token,这里使用authenticate进行校验是否存在该用户 def login(request):try:data json.loads(request.body)username data.get(username)password data.get(password)if not all([username, password]):return to_response(status400, msg参数…...
)
❤️算法笔记❤️-(每日一刷-26、删除有序数组的重复项)
文章目录 题目思路解法 题目 给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯…...

银河麒麟系统安装设备类型选择lvm简单模式之后,数据写入导致失败导致系统重启无法正常加载
银河麒麟系统安装设备类型选择lvm简单模式之后,数据写入导致失败导致系统重启无法正常加载 一 系统环境1.1 系统版本信息1.2 通过镜像安装的过程中选择设备类型选择的是lvm简单模式 二 问题描述三 问题修复过程3.1 挂载ISO镜像,引导到字符终端界面3.2 修…...
Mybatis-核心配置文件 / Mybatis增删改查
1. 核心配置文件 1.1. 概述 核心配置文件是MyBatis框架中用于集中定义全局配置信息的XML文件,其内部包含了一系列预设标签,用于设置数据库连接、对象映射、类型处理等关键参数。这些标签遵循特定的排列顺序,尽管并非所有标签都是强制性的&a…...
)
Nginx(面试)
NGINX 速记问答 Q 什么是Nginx?它的主要特点是什么? A Nginx是一个高性能的开源Web服务器和反向代理服务器。它以高并发、低内存消耗和高稳定性著称。 Q Nginx与Apache Web服务器有什么区别? A Nginx与Apache相比,更适用于处…...

net::ERR_SSL_PROTOCOL_ERROR
小程序 发起网络请求 解决: 如果还没有申请SSL证书,那就直接把https请求改为http 测试可以用 上线不推荐...
)
BaseDao封装增删改查(超详解)
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍对数据库中表中的数据进行增改删查询,封装一个工具类(BaseDao)的详细使用以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 &…...

【Python操作基础】——元组
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972 个人介绍: 研一|统计学|干货分享 擅长Python、Matlab、R等主流编程软件 累计十余项国家级比赛奖项,参与研究经费10w、40w级横向 文…...

光伏投融资该如何计算?
光伏投融资是光伏产业发展过程中的重要环节,其计算涉及到多个方面,包括项目规模、预期收益、成本分析、风险评估等。合理的投融资计算能够为光伏项目的实施提供资金保障,同时也能够降低投资风险,提高项目的经济效益。 首先&#x…...

【更新中】Leetcode中遇到的最短路径算法
dijsktra算法模板: def dijkstra(x):#x表示出发点dis[inf]*n #dis记录从x出发到各个点的最短距离,初始化为infdis[x]0 #源点到自己的距离为0vis[False]*n #检查各个点是否访问过for _ in range(n-1): #检查除了源点的其他n-1个点,更新dis…...

Git学习笔记之基础
本笔记是阅读《git pro》所写,仅供参考。 《git pro》网址https://git-scm.com/book/en/v2 git官网 https://git-scm.com/ 一、git起步 1.1、检查配置信息 git config --list查看所有的配置以及它们所在的文件 git config --list --show-origin可能有重复的变量名…...

STCubeIDE 编译bootloader
头文件重复引用解决办法。 参考:STM32CubeIDE IAP原理讲解,及UART双APP交替升级IAP实现-CSDN博客 移植到Air32时,RAM的大小(无论boot程序还是app 程序) 尽量不动,如果动了会影响最终的 APP 跳转 flash 大小可以随意修改…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
