【动手学深度学习】深入浅出深度学习之线性神经网络



目录
🌞一、实验目的
🌞二、实验准备
🌞三、实验内容
🌼1. 线性回归
🌻1.1 矢量化加速
🌻1.2 正态分布与平方损失
🌼2. 线性回归的从零开始实现
🌻2.1. 生成数据集
🌻2.2 读取数据集
🌻2.3. 初始化模型参数
🌻2.4. 定义模型
🌻2.5. 定义损失函数
🌻2.6. 定义优化算法
🌻2.7. 训练
🌻2.8 小结
🌻2.9 练习
🌼3. 线性回归的简洁实现
🌻3.1. 生成数据集
🌻3.2. 读取数据集
🌻3.3 定义模型
🌻3.4 初始化模型参数
🌻3.5 定义损失函数
🌻3.6 定义优化算法
🌻3.7 训练
🌻3.8 小结
🌻3.9 练习
🌞四、实验心得
🌞一、实验目的
- 熟悉PyTorch框架:了解PyTorch的基本概念、数据结构和核心函数;
- 创建线性回归模型:使用PyTorch构建一个简单的线性回归模型,该模型能够学习输入特征和目标变量之间的线性关系;
- 线性回归从零开始实现及其简洁实现,并完成章节后习题。
🌞二、实验准备
- 根据GPU安装pytorch版本实现GPU运行实验代码;
- 配置环境用来运行 Python、Jupyter Notebook和相关库等相关库。
🌞三、实验内容
资源获取:关注公众号【科创视野】回复 深度学习
🌼1. 线性回归
(1)使用jupyter notebook新增的pytorch环境新建ipynb文件,完成线性回归从零开始实现的实验代码与练习结果如下:
🌻1.1 矢量化加速
%matplotlib inline
import math
import time
import numpy as np
import torch
from d2l import torch as d2ln = 10000
a = torch.ones([n])
b = torch.ones([n])class Timer: #@save"""记录多次运行时间"""def __init__(self):self.times = []self.start()def start(self):"""启动计时器"""self.tik = time.time()def stop(self):"""停止计时器并将时间记录在列表中"""self.times.append(time.time() - self.tik)return self.times[-1]def avg(self):"""返回平均时间"""return sum(self.times) / len(self.times)def sum(self):"""返回时间总和"""return sum(self.times)def cumsum(self):"""返回累计时间"""return np.array(self.times).cumsum().tolist()c = torch.zeros(n)
timer = Timer()
for i in range(n):c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'输出结果

🌻1.2 正态分布与平方损失
def normal(x, mu, sigma):p = 1 / math.sqrt(2 * math.pi * sigma**2)return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)# 再次使用numpy进行可视化
x = np.arange(-7, 7, 0.01)# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',ylabel='p(x)', figsize=(4.5, 2.5),legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])输出结果

🌼2. 线性回归的从零开始实现
%matplotlib inline
import random
import torch
from d2l import torch as d2l🌻2.1. 生成数据集
def synthetic_data(w, b, num_examples): #@save"""生成y=Xw+b+噪声"""X = torch.normal(0, 1, (num_examples, len(w)))y = torch.matmul(X, w) + by += torch.normal(0, 0.01, y.shape)return X, y.reshape((-1, 1))true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)print('features:', features[0],'\nlabel:', labels[0])输出结果

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);输出结果
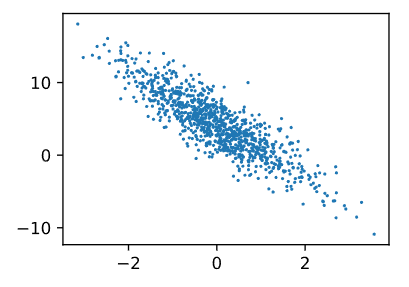
🌻2.2 读取数据集
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))# 这些样本是随机读取的,没有特定的顺序random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices], labels[batch_indices]batch_size = 10for X, y in data_iter(batch_size, features, labels):print(X, '\n', y)break输出结果

🌻2.3. 初始化模型参数
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
w,b输出结果

🌻2.4. 定义模型
def linreg(X, w, b): #@save"""线性回归模型"""return torch.matmul(X, w) + b🌻2.5. 定义损失函数
def squared_loss(y_hat, y): #@save"""均方损失"""return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2🌻2.6. 定义优化算法
def sgd(params, lr, batch_size): #@save"""小批量随机梯度下降"""with torch.no_grad():for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()🌻2.7. 训练
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_lossfor epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y) # X和y的小批量损失# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,# 并以此计算关于[w,b]的梯度l.sum().backward()sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')输出结果

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')输出结果

🌻2.8 小结
我们学习了深度网络是如何实现和优化的。在这一过程中只使用张量和自动微分,不需要定义层或复杂的优化器。这一节只触及到了表面知识。在下面的部分中,我们将基于刚刚介绍的概念描述其他模型,并学习如何更简洁地实现其他模型。
🌻2.9 练习
1.如果我们将权重初始化为零,会发生什么。算法仍然有效吗?
# 在单层网络中(一层线性回归层),将权重初始化为零时可以的,但是网络层数加深后,在全连接的情况下,
# 在反向传播的时候,由于权重的对称性会导致出现隐藏神经元的对称性,使得多个隐藏神经元的作用就如同
# 1个神经元,算法还是有效的,但是效果不大好。参考:https://zhuanlan.zhihu.com/p/75879624。2.假设试图为电压和电流的关系建立一个模型。自动微分可以用来学习模型的参数吗?
# 可以的,建立模型U=IW+b,然后采集(U,I)的数据集,通过自动微分即可学习W和b的参数。
import torch
import random
from d2l import torch as d2l
#生成数据集
def synthetic_data(r, b, num_examples):I = torch.normal(0, 1, (num_examples, len(r)))u = torch.matmul(I, r) + bu += torch.normal(0, 0.01, u.shape) # 噪声return I, u.reshape((-1, 1)) # 标量转换为向量true_r = torch.tensor([20.0])
true_b = 0.01
features, labels = synthetic_data(true_r, true_b, 1000)#读取数据集
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices],labels[batch_indices]batch_size = 10
# 初始化权重
r = torch.normal(0,0.01,size = ((1,1)), requires_grad = True)
b = torch.zeros(1, requires_grad = True)# 定义模型
def linreg(I, r, b):return torch.matmul(I, r) + b
# 损失函数
def square_loss(u_hat, u):return (u_hat - u.reshape(u_hat.shape)) ** 2/2
# 优化算法
def sgd(params, lr, batch_size):with torch.no_grad():for param in params:param -= lr * param.grad/batch_sizeparam.grad.zero_()lr = 0.03
num_epochs = 10
net = linreg
loss = square_lossfor epoch in range(num_epochs):for I, u in data_iter(batch_size, features, labels):l = loss(net(I, r, b), u)l.sum().backward()sgd([r, b], lr, batch_size)with torch.no_grad():train_l = loss(net(features, r, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
print(r)
print(b)
print(f'r的估计误差: {true_r - r.reshape(true_r.shape)}')
print(f'b的估计误差: {true_b - b}')
输出结果

3.能基于普朗克定律使用光谱能量密度来确定物体的温度吗?
# 3
# 普朗克公式
# x:波长
# T:温度
import torch
import random
from d2l import torch as d2l#生成数据集
def synthetic_data(x, num_examples):T = torch.normal(0, 1, (num_examples, len(x)))u = c1 / ((x ** 5) * ((torch.exp(c2 / (x * T))) - 1));u += torch.normal(0, 0.01, u.shape) # 噪声return T, u.reshape((-1, 1)) # 标量转换为向量c1 = 3.7414*10**8 # c1常量
c2 = 1.43879*10**4 # c2常量
true_x = torch.tensor([500.0])features, labels = synthetic_data(true_x, 1000)#读取数据集
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices],labels[batch_indices]batch_size = 10
# 初始化权重
x = torch.normal(0,0.01,size = ((1,1)), requires_grad = True)# 定义模型
def planck_formula(T, x):return c1 / ((x ** 5) * ((torch.exp(c2 / (x * T))) - 1))
# 损失函数
def square_loss(u_hat, u):return (u_hat - u.reshape(u_hat.shape)) ** 2/2
# 优化算法
def sgd(params, lr, batch_size):with torch.no_grad():for param in params:param -= lr * param.grad/batch_sizeparam.grad.zero_()lr = 0.001
num_epochs = 10
net = planck_formula
loss = square_lossfor epoch in range(num_epochs):for T, u in data_iter(batch_size, features, labels):l = loss(net(T, x), u)l.sum().backward()sgd([x], lr, batch_size)with torch.no_grad():train_l = loss(net(features, x), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')print(f'r的估计误差: {true_x - x.reshape(true_x.shape)}')
输出结果

4.计算二阶导数时可能会遇到什么问题?这些问题可以如何解决?
# 一阶导数的正向计算图无法直接获得,可以通过保存一阶导数的计算图使得可以求二阶导数(create_graph和retain_graph都置为True,
# 保存原函数和一阶导数的正向计算图)。实验如下:
import torchx = torch.randn((2), requires_grad=True)
y = x**3dy = torch.autograd.grad(y, x, grad_outputs=torch.ones(x.shape),retain_graph=True, create_graph=True)
dy2 = torch.autograd.grad(dy, x, grad_outputs=torch.ones(x.shape))dy_ = 3*x**2
dy2_ = 6*xprint("======================================================")
print(dy, dy_)
print("======================================================")
print(dy2, dy2_)
输出结果

5.为什么在squared_loss函数中需要使用reshape函数?
# 以防y^和y,一个是行向量、一个是列向量,使用reshape,可以确保shape一样。6.尝试使用不同的学习率,观察损失函数值下降的快慢。
# ①学习率过大前期下降很快,但是后面不容易收敛;
# ②学习率过小损失函数下降会很慢。7.如果样本个数不能被批量大小整除,data_iter函数的行为会有什么变化?
# 报错。🌼3. 线性回归的简洁实现
(1)使用jupyter notebook新增的pytorch环境新建ipynb文件,完成线性回归的简洁实现的实验代码与练习结果如下:
🌻3.1. 生成数据集
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2ltrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)🌻3.2. 读取数据集
def load_array(data_arrays, batch_size, is_train=True): #@save"""构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features, labels), batch_size)next(iter(data_iter))输出结果

🌻3.3 定义模型
# nn是神经网络的缩写
from torch import nnnet = nn.Sequential(nn.Linear(2, 1))🌻3.4 初始化模型参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)输出结果
![]()
🌻3.5 定义损失函数
loss = nn.MSELoss()🌻3.6 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)🌻3.7 训练
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X) ,y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')输出结果

w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)输出结果
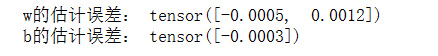
🌻3.8 小结
- 我们可以使用PyTorch的高级API更简洁地实现模型。
- 在PyTorch中,data模块提供了数据处理工具,nn模块定义了大量的神经网络层和常见损失函数。
- 我们可以通过_结尾的方法将参数替换,从而初始化参数。
🌻3.9 练习
1.如果将小批量的总损失替换为小批量损失的平均值,需要如何更改学习率?
# 将学习率除以batchsize。2.查看深度学习框架文档,它们提供了哪些损失函数和初始化方法?
用Huber损失代替原损失,即
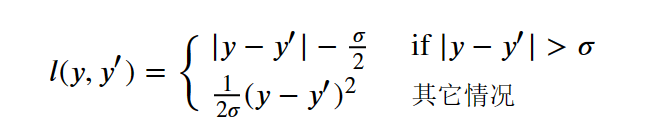
# Huber损失可以用torch自带的函数解决
torch.nn.SmoothL1Loss()
# 也可以自己写
import torch.nn as nn
import torch.nn.functional as Fclass HuberLoss(nn.Module):def __init__(self, sigma):super(HuberLoss, self).__init__()self.sigma = sigmadef forward(self, y, y_hat):if F.l1_loss(y, y_hat) > self.sigma:loss = F.l1_loss(y, y_hat) - self.sigma/2else:loss = (1/(2*self.sigma))*F.mse_loss(y, y_hat)return loss#%%
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l#%%
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)def load_array(data_arrays, batch_size, is_train = True): #@save'''pytorch数据迭代器'''dataset = data.TensorDataset(*data_arrays) # 把输入的两类数据一一对应;*表示对list解开入参return data.DataLoader(dataset, batch_size, shuffle = is_train) # 重新排序batch_size = 10
data_iter = load_array((features, labels), batch_size) # 和手动实现中data_iter使用方法相同#%%
# 构造迭代器并验证data_iter的效果
next(iter(data_iter)) # 获得第一个batch的数据#%% 定义模型
from torch import nn
net = nn.Sequential(nn.Linear(2, 1)) # Linear中两个参数一个表示输入形状一个表示输出形状
# sequential相当于一个存放各层数据的list,单层时也可以只用Linear#%% 初始化模型参数
# 使用net[0]选择神经网络中的第一层
net[0].weight.data.normal_(0, 0.01) # 正态分布
net[0].bias.data.fill_(0)#%% 定义损失函数
loss = torch.nn.HuberLoss()
#%% 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03) # optim module中的SGD
#%% 训练
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X), y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch+1}, loss {l:f}')#%% 查看误差
w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)
输出结果

3.如何访问线性回归的梯度?
#假如是多层网络,可以用一个self.xxx=某层,然后在外面通过net.xxx.weight.grad和net.xxx.bias.grad把梯度给拿出来。
net[0].weight.grad
net[0].bias.grad
输出结果
![]()
🌞四、实验心得
通过此次实验,我熟悉了PyTorch框架以及PyTorch的基本概念、数据结构和核心函数;创建了线性回归模型,使用PyTorch构建一个简单的线性回归模型;完成了线性回归从零开始实现及其简洁实现以及章节后习题。明白了以下几点:
1.深度学习的关键要素包括训练数据、损失函数、优化算法以及模型本身。这些要素相互作用,共同决定了模型的性能和表现。
2.矢量化是一种重要的数学表达方式,它能使数学计算更加简洁高效。通过使用向量和矩阵运算,可以将复杂的计算过程转化为简单的线性代数运算,从而提高计算效率。
3.最小化目标函数和执行极大似然估计是等价的。在机器学习中,通常通过最小化损失函数来优化模型。而在概率统计中,可以通过最大化似然函数来估计模型参数。这两种方法在数学上是等价的,都可以用于优化模型。
4.线性回归模型可以被看作是一个简单的神经网络模型。它只包含一个输入层和一个输出层,其中输入层的神经元数量与输入特征的维度相同,输出层的神经元数量为1。线性回归模型可以用于解决回归问题,通过学习输入特征与输出之间的线性关系来进行预测。
5.在深度学习中,学习了如何实现和优化深度神经网络。在这个过程中,只使用张量(Tensor)和自动微分(Automatic Differentiation),而不需要手动定义神经网络层或复杂的优化器。张量是深度学习中的基本数据结构,它可以表示多维数组,并支持各种数学运算。自动微分是一种计算梯度的技术,它能够自动计算函数相对于输入的导数,从而实现了反向传播算法。
6.为了更加简洁地实现模型,可以利用PyTorch的高级API。在PyTorch中,data模块提供了数据处理工具,包括数据加载、预处理和批处理等功能,使得数据的处理变得更加方便和高效。nn模块则提供了大量的神经网络层和常见损失函数的定义,可以直接使用这些层和函数来构建和训练模型,无需手动实现。此外还可以通过使用_结尾的方法来进行参数的替换和初始化,从而更加灵活地管理模型的参数。


相关文章:

【动手学深度学习】深入浅出深度学习之线性神经网络
目录 🌞一、实验目的 🌞二、实验准备 🌞三、实验内容 🌼1. 线性回归 🌻1.1 矢量化加速 🌻1.2 正态分布与平方损失 🌼2. 线性回归的从零开始实现 🌻2.1. 生成数据集 &#x…...
2024/3/26 C++作业
定义一个矩形类(Rectangle),包含私有成员:长(length)、宽(width), 定义成员函数: 设置长度:void set_l(int l) 设置宽度:void set_w(int w) 获取长度:int…...

LinkedList讲解指南
咦咦咦,各位小可爱,我是你们的好伙伴——bug菌,今天又来给大家普及Java SE相关知识点了,别躲起来啊,听我讲干货还不快点赞,赞多了我就有动力讲得更嗨啦!所以呀,养成先点赞后阅读的好…...

IP如何异地共享文件?
【天联】 组网由于操作简单、跨平台应用、无网络要求、独创的安全加速方案等原因,被几十万用户广泛应用,解决了各行业客户的远程连接需求。采用穿透技术,简单易用,不需要在硬件设备中端口映射即可实现远程访问。 异地共享文件 在…...

HCIA-Datacom H12-811 题库补充(3/28)
完整题库及答案解析,请直接扫描上方二维码,持续更新中 OSPFv3使用哪个区域号标识骨干区域? A:0 B:3 C:1 D:2 答案:A 解析:AREA 号0就是骨干区域。 STP下游设备通知上游…...

轻量级富文本编辑 Trumbowyg —— 基于 jQuery 插件配置
使用方法👇 首先,添加jQuery到页面<body>位置: <script src"http://libs.baidu.com/jquery/1.8.3/jquery.min.js"></script> <script>window.jQuery || document.write(<script src"js/vendor/jquery-1.10.2.min.js&qu…...
那些王道书里的题目-----计算机网络篇
注:仅记录个人认为有启发的题目 p155 34.下列四个地址块中,与地址块 172.16.166.192/26 不重叠,且与172.16.166.192/26聚合后的地址块不会引入多余地址的是() A.172.16.166.192/27 B.172.16.166.128/26 …...

【前端学习——js篇】 10.this指向
具体见:https://github.com/febobo/web-interview 10.this指向 根据不同的使用场合,this有不同的值,主要分为下面几种情况: 默认绑定隐式绑定new绑定显示绑定 ①默认绑定 全局环境中定义person函数,内部使用this关…...

项目搭建之统一返回值
自定义枚举类 Getter public enum ReturnCodeEnum {/*** 操作失败**/RC999("999","操作XXX失败"),/*** 操作成功**/RC200("200","success"),/*** 服务降级**/RC201("201","服务开启降级保护,请稍后再试!"),/*** …...

嵌入式和 Java 走哪条路?
最近看到一个物联网大三学生的疑问,原话如下: 本人普通本科物联网工程专业,开学大三,现在就很迷茫,不打算考研了,准备直接就业,平时一直在实验室参加飞思卡尔智能车比赛,本来是想走嵌…...

C++ 控制语句(一)
一 顺序结构 程序的基本结构有三种: 顺序结构、分支结构、循环结构 大量的实际问题需要通过各种控制流程来解决。 1.1 顺序结构 1.2 简单语句和复合语句 二 循环 2.1 for循环 语句流程图 注意:使用for语句的灵活性 三 while语句 四 do while语句...

mysql 用户管理-权限表
学习了《mysql5.7安装》,就先再了解下用户管理,先了解下权限表。 MySQL是一个多用户数据库,具有功能强大的访问控制系统,可以为不同用户指定允许 的权限。MySQL用户可以分为普通用户和root用户。root 用户是超级管理员,拥有所有权…...
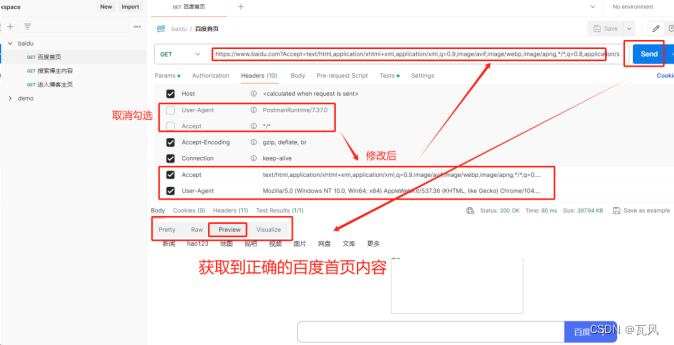
【Postman如何进行接口测试简单详细操作实例】
1、下载Postman postman下载地址:Download Postman | Get Started for Free 2、安装Postman (1)双击下载好的postman-setup.exe文件,进行安装postman工具 (2)安装完成后,在桌面找到并打开postman软件,输入邮箱和密码进行登录&a…...

docker搭建Project Calico环境
Project Calico 是一个开源的网络和网络安全解决方案,专为容器、虚拟机和本地工作负载设计。它提供了高度可扩展的网络层,支持广泛的容器编排平台,如 Kubernetes、Docker Swarm和OpenStack。Calico 的主要特点包括: 支持多层网络策略,包括基于角色的访问控制(RBAC)。提供网…...

pyecharts操作一
pyecharts 是一个用于生成Echarts图表的Python库。Echarts是百度开源的一个数据可视化JS库,可以生成一些非常酷炫的图表。 环境安装 pip install pyecharts 检查版本 import pyecharts print(pyecharts.version) 2.0.3 柱状图绘制 from pyecharts.charts impor…...

『Apisix进阶篇』动态负载均衡:APISIX的实战演练与策略应用
🚀『Apisix系列文章』探索新一代微服务体系下的API管理新范式与最佳实践 【点击此跳转】 📣读完这篇文章里你能收获到 🎯 掌握APISIX中多种负载均衡策略的原理及其适用场景。📈 学习如何通过APISIX的Admin API和Dashboard进行负…...

【开发篇】十一、GC调优的分析工具
文章目录 1、调优的主要指标2、工具一:jstat3、工具二:Visual VM的插件4、工具三:Prometheus Grafana5、生成GC日志6、工具四:GC Viewer7、工具五:GCeasy GC调优,是为了避免因垃圾回收引起程序性能下降&am…...
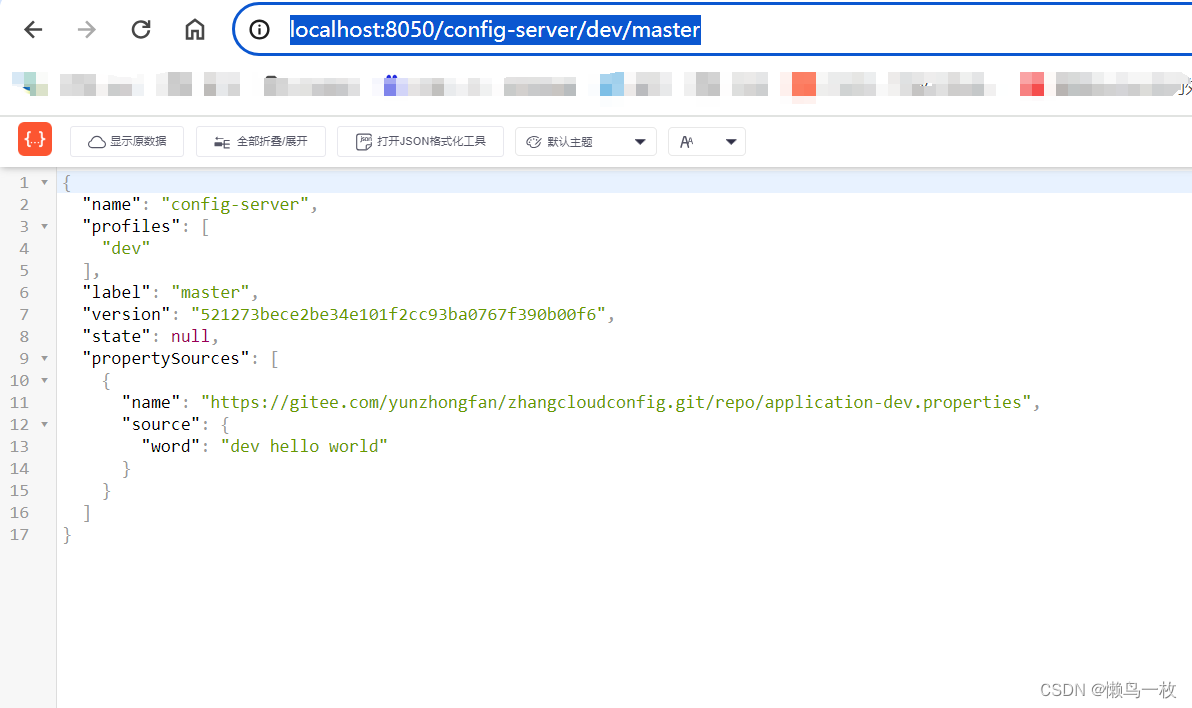
SpringCloudConfig 使用git搭建配置中心
一 SpringCloudConfig 配置搭建步骤 1.引入 依赖pom文件 引入 spring-cloud-config-server 是因为已经配置了注册中心 <dependencies><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-config-server</…...

c#基础-引用类型和值类型的区别
在C#中,数据类型分为两类:值类型和引用类型。 值类型:直接存储数据,分配在栈(Stack)上。常见的值类型包括基本数据类型(int, float, double等),结构体(struct),枚举(enum)等。 引用类型:存储数据的引用和对象,分配在托管堆(Heap)上。常见的引用类型包括类(cla…...

面试题-3.20
1、__FILE__表示什么意思? __FILE__:当前文件的完整路径和文件名 __LINE__:当前行 __DIR__:当前文件所在的目录 2、如何获取客户端的IP地址? 通过超全局数组$_SERVER:echo $_SERVER[REMOTE_PORT]; 3、写…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
