【数据结构】最小生成树(Prim算法,普里姆算法,普利姆)、最短路径(Dijkstra算法,迪杰斯特拉算法,单源最短路径)
文章目录
- 前置问题
- 问题解答
- 一、基础概念:最小生成树的定义和性质
- (1)最小生成树(Minimal Spanning Tree)的定义
- (2)最小生成树(MST)的性质
- 二、如何利用MST性质寻找最小生成树
- 三、Prim算法
- (1)Prim算法思想
- (2)Prim算法形成最小生成树的详细过程
- (3)Prim算法的C++和python实现
- 四、Dijkstra算法
- (1)和Prim算法的联系
- (2)Dijkstra算法思想
前置问题


问题解答

一、基础概念:最小生成树的定义和性质
(1)最小生成树(Minimal Spanning Tree)的定义
生成树的代价:设G(V,E)G(V,E)G(V,E)是一个无向连通网图,生成树上各边的权值之和称为生成树的代价。最小生成树:在图GGG所有生成树中,代价最小的生成树为最小生成树。
(2)最小生成树(MST)的性质
假设G=(V,E)G=(V,E)G=(V,E)是一个无向连通网图,UUU是顶点集的一个非空子集。若(u,v)(u,v)(u,v)是一条具有最小权值的边,其中u∈U,v∈V−Uu\in U,v\in V-Uu∈U,v∈V−U,则必存在一棵包含边u,vu,vu,v的最小生成树。
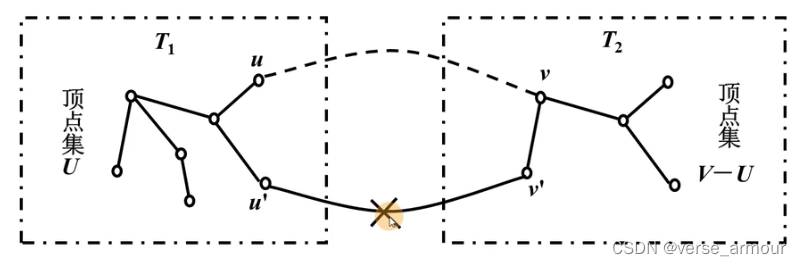
二、如何利用MST性质寻找最小生成树
- 找到两个点集之间最小权值的边(u,v)(u,v)(u,v),让具有最小权值的(u,v)(u,v)(u,v)成为最小生成树的一部分,将大于最小权值的(u,v)(u,v)(u,v)删除。
接下来有两个思路:
- 从一个点出发,一次加入点形成点集
(Prim算法) - 从边出发,将点集合并,避免形成环
(Kruskal算法)
三、Prim算法
(1)Prim算法思想
对点做操作,维护一个在最小生成树中的点的顶点集A,以及一个待处理点的顶点集B,每次找出连接这两个集合的最短边,并将其两个顶点都加入集合A,直到所有顶点都处理完毕。
抽象描述:(觉得抽象跳过)

(2)Prim算法形成最小生成树的详细过程
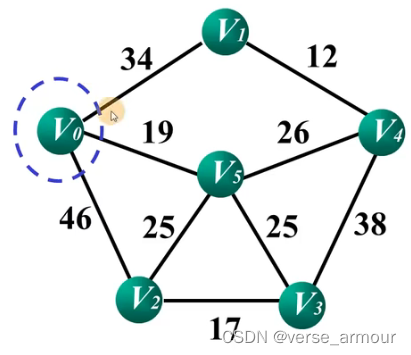
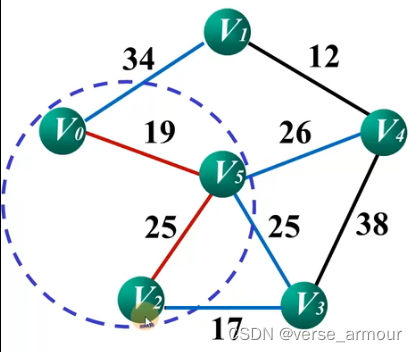
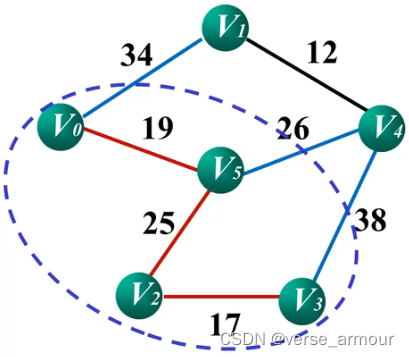
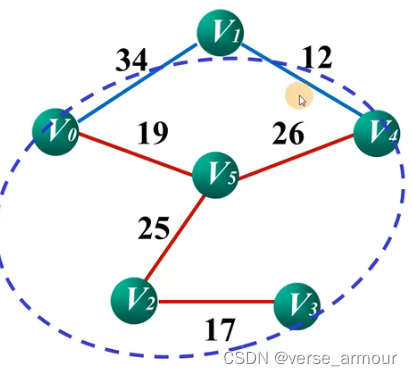
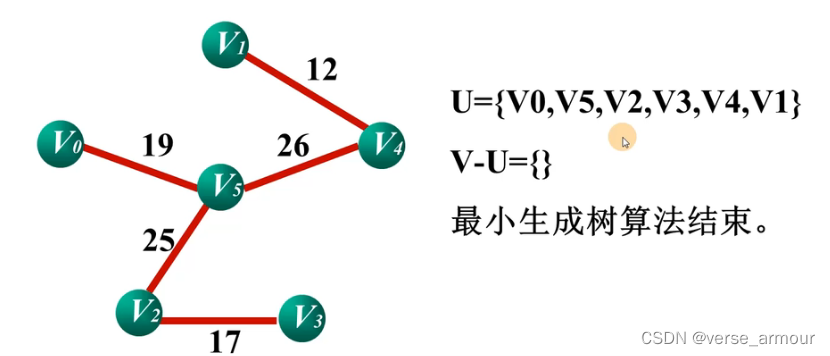
图注:
- 红色线段表示最小生成树
- 蓝圈表示集合UUU,其他顶点集合为V−UV-UV−U
- 蓝色线段表示UUU和V−UV-UV−U的相邻边

计算U中每个点和其相邻点之间的代价,找出代价最小的点V5,将V5纳入U集合。计算U中每个点和其相邻点之间的代价,找出代价最小的点V5,将V5纳入U集合。计算U中每个点和其相邻点之间的代价,找出代价最小的点V5,将V5纳入U集合。
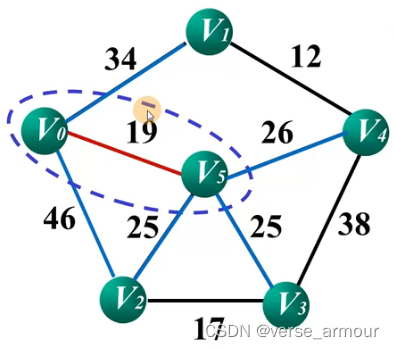
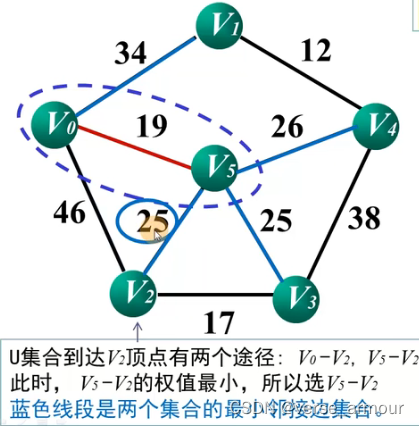


(3)Prim算法的C++和python实现
四、Dijkstra算法
(1)和Prim算法的联系
Dijkstra算法和Prim算法都是最短路径算法,主要用于求图的最短路径。
不同点在于,Dijkstra算法适用于有向图起点到其他点的最短路径,而Prim算法适用于无向图求最小生成树。它们的求解过程也略有不同。Dijkstra算法每次选择距离起点最近的点作为新的访问点,更新其他点到起点的最短距离,直到所有点都被访问。Prim算法则从一个起点开始,不断选择与已经访问过的点相连且边权最小的点,直到图上所有点都被访问。
(2)Dijkstra算法思想
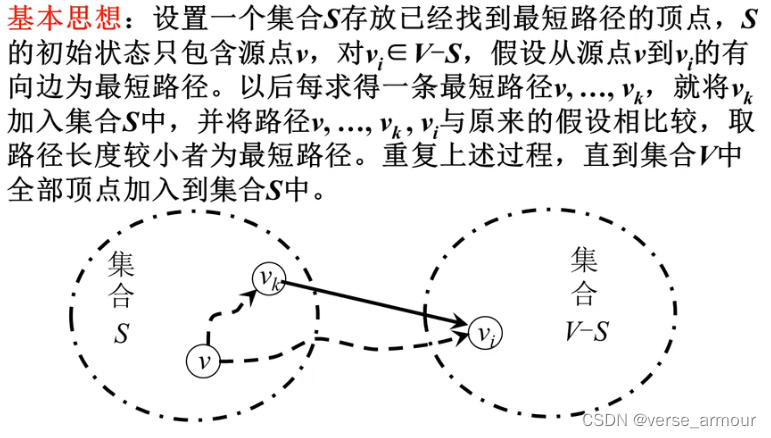
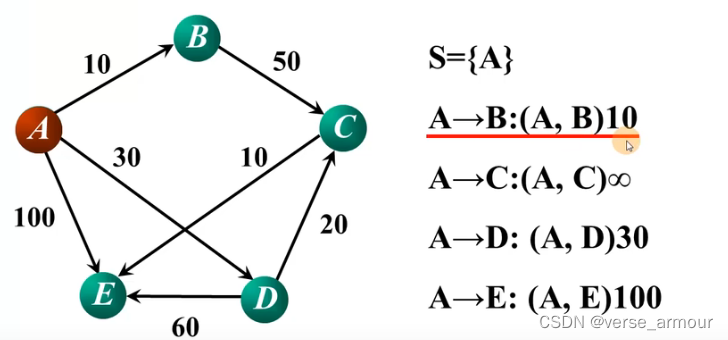
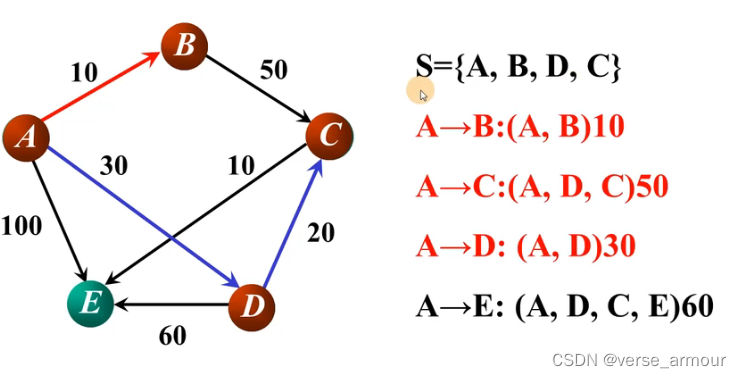
算出A点到图中每一点的路径长度,选出一条最短路径:A->B,将顶点B加入集合S。
增加了一条最短路径之后,顶点A到其他点的路径是不是有更短的路径了呢?
更新最短路径:
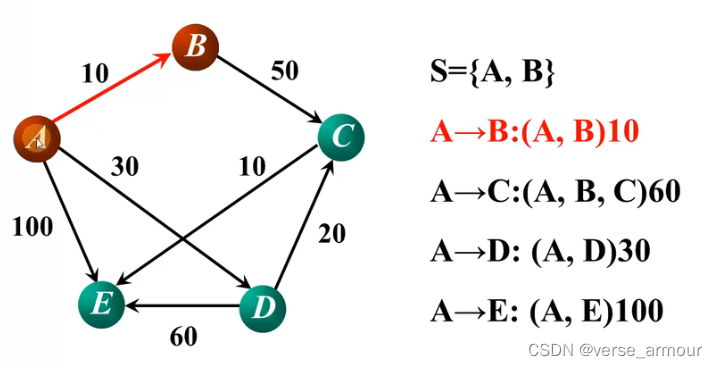
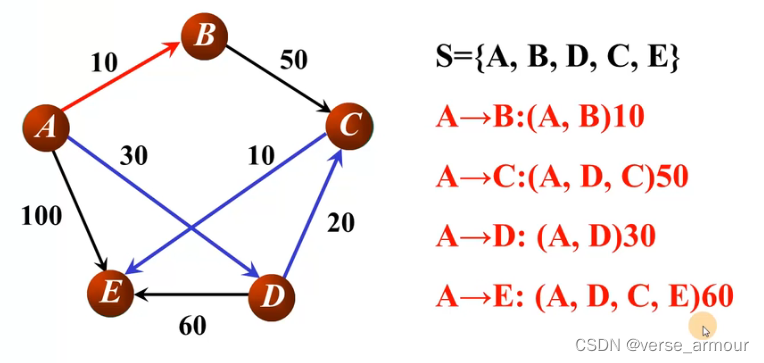
在A->C,A->D,A->E中选出最短路径:A->D,并将D顶点加入S集合。更新所有最短路径。
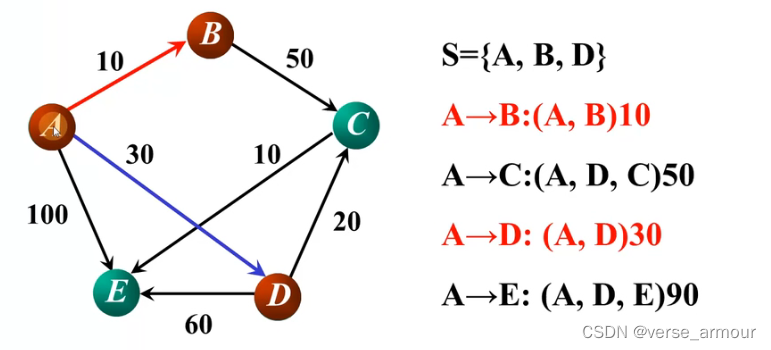
相关文章:

【数据结构】最小生成树(Prim算法,普里姆算法,普利姆)、最短路径(Dijkstra算法,迪杰斯特拉算法,单源最短路径)
文章目录前置问题问题解答一、基础概念:最小生成树的定义和性质(1)最小生成树(Minimal Spanning Tree)的定义(2)最小生成树(MST)的性质二、如何利用MST性质寻找最小生成树…...
)
Session与Cookie的区别(一)
从我刚开始学程序时这一题就常出现在面试考题里,一直到现在都还是能看见这个问题。 这个问题重要吗?我觉得蛮重要的。因为 Session 所代表的是「状态」,如果没有了状态,一大堆功能都会失效。 对于工程师来说必须去理解什么是 Sess…...

【Java】重载和重写的区别
重载(Overload) 在同一个类中,同名的方法如果有不同的参数列表(参数类型不同、参数个数不同甚至是参数顺序不同)则视为重载。同时,重载对返回类型没有要求,可以相同也可以不同,但不能通过返回类型是否相同…...

AcWing 第 90 场周赛
目录A、首字母大写B、找数字C、构造字符串A、首字母大写 原题链接:AcWing 4806. 首字母大写 签到题。 #include <bits/stdc.h>using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);string s;cin >> s;s[0] toupper(s[0]);…...

刚刚,体验了一把Bing chat很爽
文章目录刚刚,体验了一把Bing chat很爽你能做啥?与chatgpt有什么不同?以下是Bingchat的 10个新功能1⃣️在网上搜索结果2⃣️摘要链接3⃣️对话助手4⃣️向您发送实际信息,正确的链接5⃣️在单个查询中执行多个搜索6⃣️玩冒险游戏…...

牛客网Python篇数据分析习题(二)
1.现有一个Nowcoder.csv文件,它记录了牛客网的部分用户数据,包含如下字段(字段与字段之间以逗号间隔): Nowcoder_ID:用户ID Level:等级 Achievement_value:成就值 Num_of_exercise&a…...
如何用Python打包好exe文件,并替换图标
前言 Python打包?打包exe文件?怎么操作? ok,今天我来分享分享,教你们如何打包号文件,顺便还来展示一下,如何替换好图标 首先把你的代码准备好,尽量不要中文路径,容易报…...

NFC概述摘要
同学,别退出呀,我可是全网最牛逼的 WIFI/BT/GPS/NFC分析博主,我写了上百篇文章,请点击下面了解本专栏,进入本博主主页看看再走呗,一定不会让你后悔的,记得一定要去看主页置顶文章哦。 原理来说,NFC和Wi-Fi类似,利用无线射频技术来实现设备间通信。NFC的工作频率为13.5…...
Python-项目实战--贪吃蛇小游戏(1)
1.贪吃蛇游戏规则贪吃蛇游戏规则如下:1.1开始和结束贪吃蛇初始出现在游戏窗口的左上角位置,体长共有3节游戏过程中,一旦蛇头撞到了窗口的边缘或者身体的其他部位,游戏结束游戏过程中,点击游戏窗口的关闭按钮,或者按下ESC键可以直接退出游戏一…...
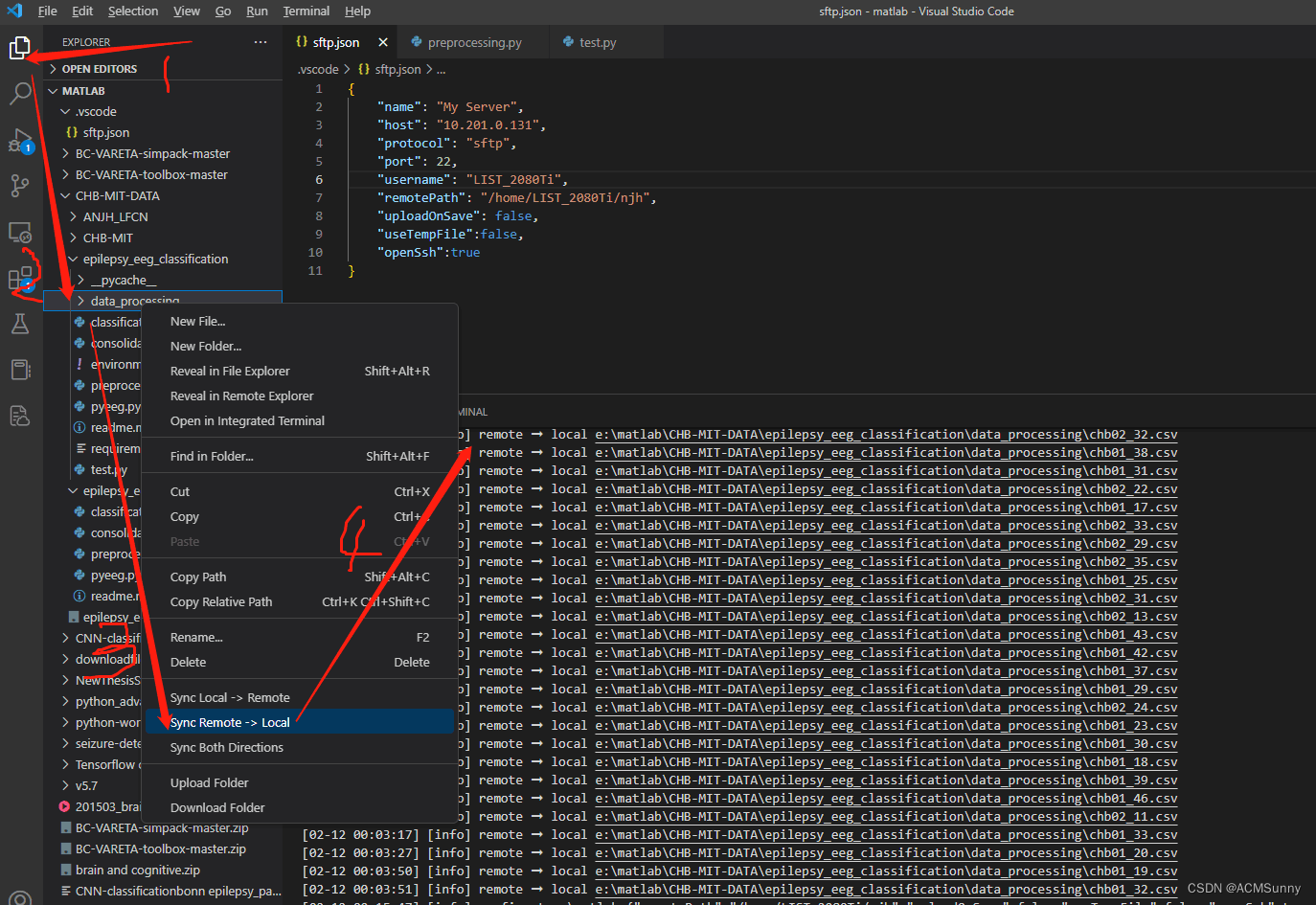
vscode sftp从linux服务器下载文件至本地:No such file or dictionary【已解决】
在服务器跑完程序需要下载数据的时候报错: [warn] ENOENT: no such file or directory, open /home/LIST_2080Ti/.ssh/config load /home/LIST_2080Ti/.ssh/config failed 完整报错内容如下: [02-10 08:38:47] [info] config at /home/LIST_2080Ti {&q…...
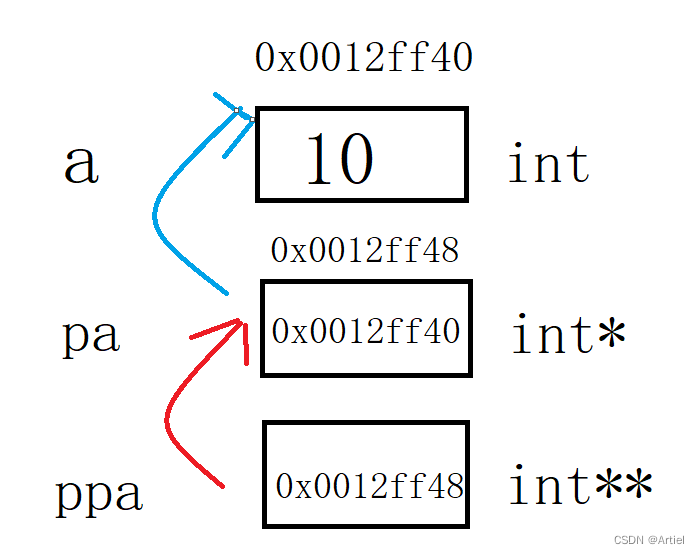
详解指针(2)(初阶版)
前言:内容包括:指针运算,指针和数组,二级指针,指针数组 详解指针(1)(点击即跳转) part 1:指针运算 1 指针-整数 以如下代码为例:初始化数组内容…...
超详细讲解字符串查找函数(保姆级教程!!!)
超详细讲解字符串查找函数(保姆级教程!!!)字符串查找函数strstr函数strstr函数的使用strstr函数的模拟实现strtok函数strtok函数的使用strtok函数的模拟实现strpbrk函数strpbrk函数的使用strpbrk函数的模拟实现strcspn…...

LeetCode-1138. 字母板上的路径【哈希表,字符串】
LeetCode-1138. 字母板上的路径【哈希表,字符串】题目描述:解题思路一:首先考虑坐标位置,字符是有序的从0开始,当前字符c的行为(c-a)/5,列为(c-a)%5。其次是考虑特殊情况z。若当前从‘z’开始则只能往上走;若是其他字符…...
)
Vue 可配置化的路由缓存(Vu2 Vue3)
Vue 可配置化的路由缓存(Vu2 & Vue3) 1 介绍 在Vue的项目当中,路由缓存是一个比较常见的功能,譬如,从列表页面进入到详情页面,返回到列表页面时,如果可以保持列表的状态,那用户…...

Linux VPU驱动
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 概述 VPU 是用来进行图像、视频数据进行硬件编、解码的硬件模块。内部集成了 Encoder、Decoder 功能部件进行图像、视频数据进行硬件编、解码&a…...
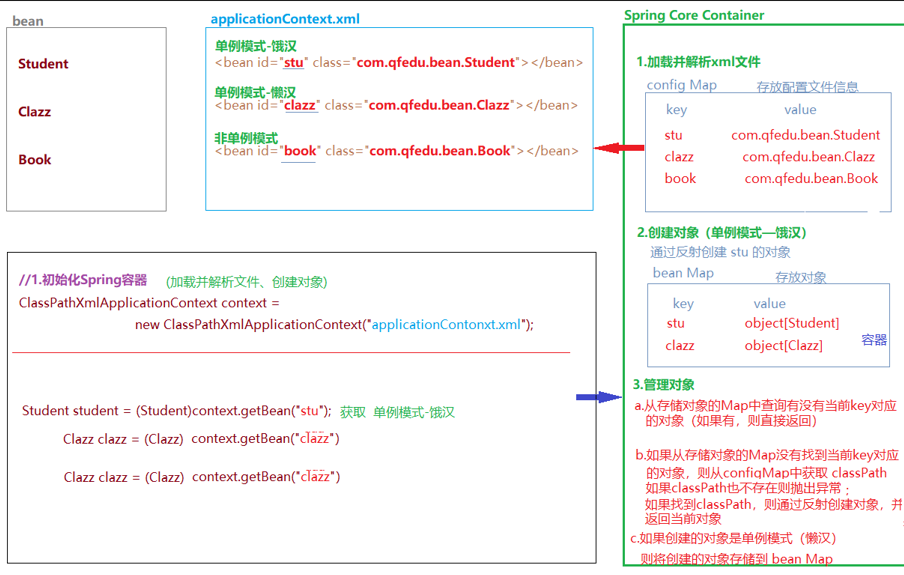
spring 笔记
一、spring概述 1.1 spring介绍 spring是一个轻量级的控制反转和面向切面的容器框架,用来解决企业项目开发的复杂度问题---解耦 轻量级:体积小,对代码没有侵入性控制反转:IOC inverse of control, 把创建对象的工作交…...

Java日志框架学习
首先,Java日志框架可以分为两类:门面型日志框架和记录型日志框架。 门面型日志框架 JCL:Java日志接口,后更名为Commons LoggingSLF4J:是一套简易Java日志门面,本身并无日志的实现 记录型日志框架 JUL&a…...

基础面试题:堆和栈的区别
面试题:堆和栈的区别(往往讲的是内存zha) 为什么说访问栈栈比访问堆快些? 目录 一、数据结构中的堆栈 1、数据结构中的堆 1)堆的定义 2)堆的效率 2、 数据结构中的栈 二、内存中的堆栈 1、内存堆的定义…...
(干货教程)在VSCode并使用chatgtp插件编写CC++语言程序
(干货教程)在VSCode并使用chatgtp插件编写CC语言程序 下载并安装VSCODE 第1步,下载VSCODE https://code.visualstudio.com/Download 第2步,安装VSCODE 安装过程较简单,这里省略。 安装好后效果如图:…...
【思维模型】概率思维的价值:找到你的人生算法,实现阶级跃迁!
把同样公平的机会放在放在很多人面前,不同的人生算法,会得到迥然不同的结果。 概率思维是什么? 【ChatGPT】概率思维是一种通过使用数学模型来思考和评估不确定性事件的方法。它通过计算不同可能性的概率来预测事件的结果,并评估风险和机会。 概率思维的价值在于它可以帮…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
