算法打卡day28|贪心算法篇02|Leetcode 122.买卖股票的最佳时机 II、55. 跳跃游戏、45.跳跃游戏 II
算法题
Leetcode 122.买卖股票的最佳时机 II
题目链接:122.买卖股票的最佳时机 II
大佬视频讲解:买卖股票的最佳时机 II视频讲解
个人思路
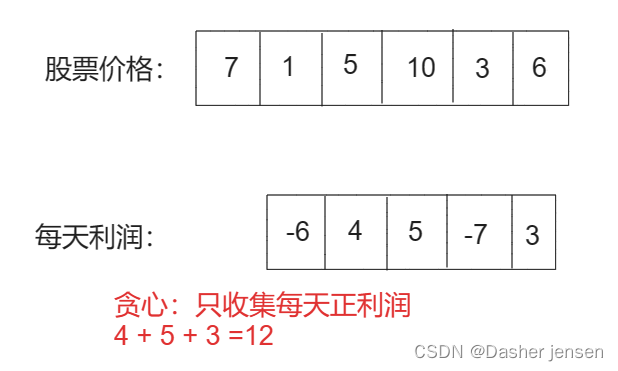
因为只有一只股票,且两天作一个交易单元,那每次只收集正利润就可以最终最多可以获取的利润,可以用贪心。
解法
贪心法
从下图可以发现,其实收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而且只需要关注最终利润,不需要记录区间。
局部最优:收集每天的正利润,全局最优:求得最大利润
class Solution {public int maxProfit(int[] prices) {int result = 0;//最终利润for (int i = 1; i < prices.length; i++) {result += Math.max(prices[i] - prices[i - 1], 0);//只收集正利润}return result;}
}时间复杂度:O(n);(遍历整个数组)
空间复杂度:O(1);(常量级的变量)
Leetcode 55. 跳跃游戏
题目链接:55. 跳跃游戏
大佬视频讲解:跳跃游戏视频讲解
个人思路
可以每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围,当覆盖范围盖过终点 就代表能跳到终点。每步取最优,最后推出全局最优,用贪心。
解法
贪心法
这个问题转化为跳跃覆盖范围究竟可不可以覆盖到终点!
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。

i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。而 cover 每次只取 max;如果 cover 大于等于了终点下标,直接 return true 。
class Solution {public boolean canJump(int[] nums) {if (nums.length == 1) {return true;}int coverRange = 0; //覆盖范围, 初始覆盖范围应该是0,因为下面的迭代是从下标0开始的//在覆盖范围内更新最大的覆盖范围for (int i = 0; i <= coverRange; i++) {coverRange = Math.max(coverRange, i + nums[i]);if (coverRange >= nums.length - 1) {//找到覆盖终点return true;}}return false;}
}时间复杂度:O(n);(遍历整个数组)
空间复杂度:O(1);(常量级的变量)
Leetcode 45.跳跃游戏 II
题目链接:45.跳跃游戏 II
大佬视频讲解:跳跃游戏 II视频讲解
个人思路
这道题和上一题思路类似;只是本题要计算最少步数。在计算时,当前可移动距离尽可能多走,如果还没到终点,步数再加一。一步尽可能多走,从而达到最少步数。局部可以推全局,用贪心。
解法
贪心法
在解题时要注意,不能真的能跳多远就跳多远,那样就不知道下一步最远能跳到哪里了。
要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数.
所以这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点.

class Solution {public int jump(int[] nums) {int result = 0;//步数int end = 0;// 当前覆盖的最远距离下标int temp = 0;// 下一步覆盖的最远距离下标//移动下标i只要遇到当前覆盖最远距离的下标,直接步数加一for (int i = 0; i <= end && end < nums.length - 1; ++i) {temp = Math.max(temp, i + nums[i]);//更新最大覆盖范围if (i == end) {// 可达位置的改变次数就是跳跃次数end = temp;result++;}}return result;}
}时间复杂度:O(n);(遍历整个数组)
空间复杂度:O(1);(常量级变量)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网
相关文章:

算法打卡day28|贪心算法篇02|Leetcode 122.买卖股票的最佳时机 II、55. 跳跃游戏、45.跳跃游戏 II
算法题 Leetcode 122.买卖股票的最佳时机 II 题目链接:122.买卖股票的最佳时机 II 大佬视频讲解:买卖股票的最佳时机 II视频讲解 个人思路 因为只有一只股票,且两天作一个交易单元,那每次只收集正利润就可以最终最多可以获取的利润…...

2013年认证杯SPSSPRO杯数学建模A题(第一阶段)护岸框架全过程文档及程序
2013年认证杯SPSSPRO杯数学建模 A题 护岸框架 原题再现: 在江河中,堤岸、江心洲的迎水区域被水流长期冲刷侵蚀。在河道整治工程中,需要在受侵蚀严重的部位设置一些人工设施,以减弱水流的冲刷,促进该处泥沙的淤积&…...

【3】3道链表力扣题:删除链表中的节点、反转链表、判断一个链表是否有环
3道链表力扣题 一、删除链表中的节点🌏 题目链接📕 示例🍀 分析💻 代码 二、反转链表🌏 题目链接📕 示例🍀 分析① 递归② 迭代 三、判断一个链表是否有环🌏 题目链接📕 …...
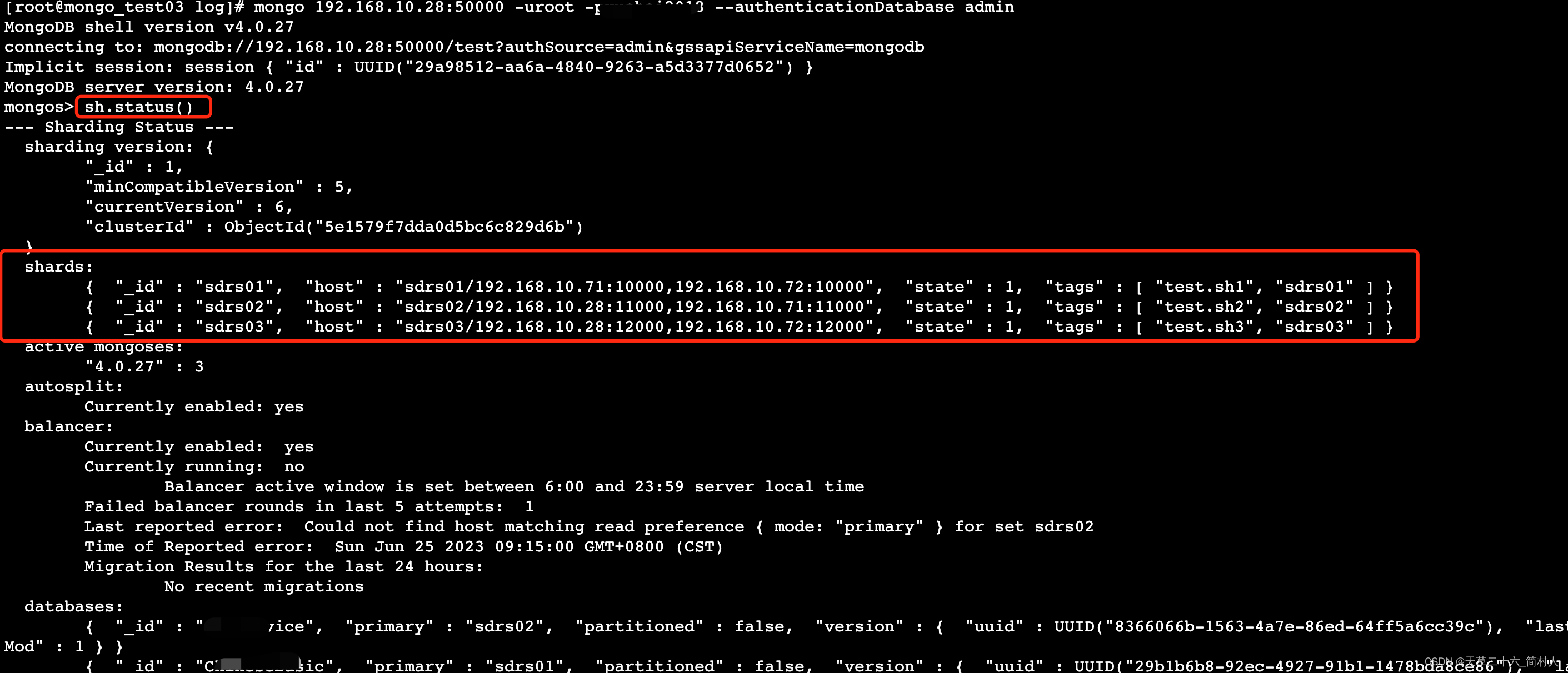
mongodb sharding分片模式的集群数据库,日志治理缺失导致写入数据库报错MongoWriteConcernException的问题总结(上)
一、背景 常见的mongodb集群模式有以下三种: 主从复制(Master-Slave)模式副本集(Replica Set)模式分片(Sharding)模式 公司测试环境搭建的集群采用分片模式,有同事反馈说…...

苹果Mac OS系统上安装brew
1.命令行安装brew Homebrew是 mac的包管理器,仅需执行相应的命令,就能下载安装需要的软件包,可以省掉自己去下载、解压、拖拽(安装)等繁琐的步骤。 a. 打开HomeBrew官网:https://brew.sh/index.html b. 点击页面上的复制按钮,打…...

应用侧渲染流程
应用侧渲染流程 《Android应用程序UI硬件加速渲染环境初始化过程分析》 https://blog.csdn.net/Luoshengyang/article/details/45769759 《Android HWUI绘制流程》 https://wizzie.top/android/android_HWUI_Draw/#1-gpu%E6%B8%B2%E6%9F%93%E7%A1%AC%E4%BB%B6%E5%8A%A0%E9%…...

学生党开放式运动耳机怎么选?五款超高销量高性价比品牌推荐
开放式运动耳机成为了许多人的运动首选装备,想要在众多的开放式耳机中找到一款价格亲民,且性能在线高性价比的开放式运动耳机可并非那么简单,所以今天我就来为大家推荐五款超高销量、高性价比的运动耳机品牌。 在推荐之前,整理了…...
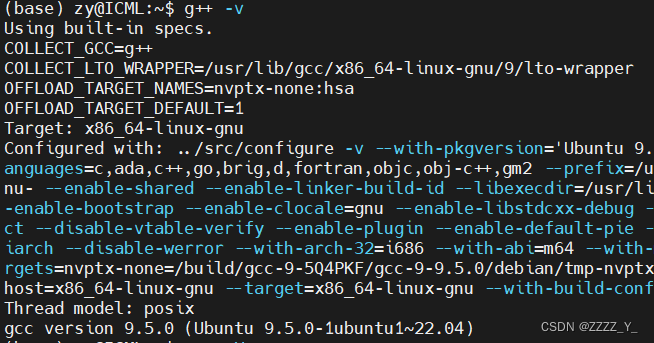
服务器中有g++,但是查询不到,Command ‘g++‘ not found
有gcc但是查询不到g,gcc版本为9.5.0 (base) zyICML:~$ g -V Command g not found, but can be installed with: apt install g Please ask your administrator. 突然就出现这个问题,导致detectron装不上,现在有时间了专门研究下怎么解决 这…...
,split() ,sys.stdin.readline() ,matrix.append, input().strip())
count(“0“),split() ,sys.stdin.readline() ,matrix.append, input().strip()
目录 count() 方法主要用于计算一个序列(例如列表、元组或字符串)中某个元素出现的次数...
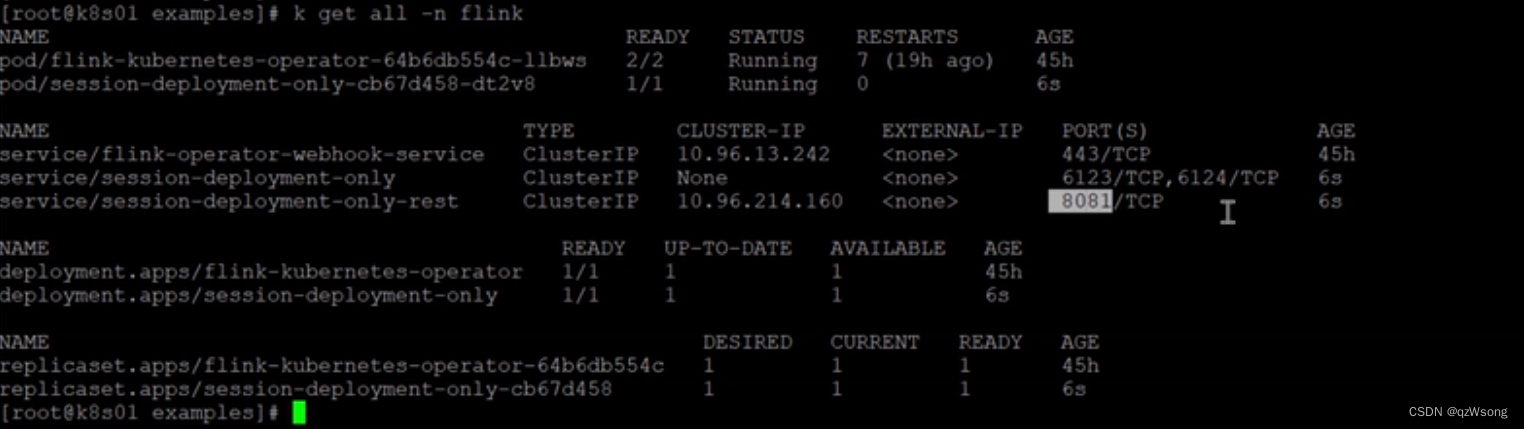
Flink on Kubernetes (flink-operator) 部署Flink
flink on k8s 官网 https://nightlies.apache.org/flink/flink-kubernetes-operator-docs-release-1.1/docs/try-flink-kubernetes-operator/quick-start/ 我的部署脚本和官网不一样,有些地方官网不够详细 部署k8s集群 注意,按照默认配置至少有两台wo…...

代码随想录算法训练营第三十二天|122.买卖股票的最佳时机II、55. 跳跃游戏、45.跳跃游戏II
122.买卖股票的最佳时机II - 🔗 讲解 - 🔗 方法一: 💡这道题自己想到的办法没有解析那么清晰,大致思路就是第一步先找到第一个可以买进的时间(也就是第一个prices[i] < prices[i 1]的i)&…...

常见数据库分类介绍及其适用场景
一、引言 数据库是指在计算机系统中,为了结构化地管理和存储数据而建立起来的一种数据管理系统。它以高效、安全和可靠的方式存储和管理用户所需的各种数据,并提供了强大的数据处理和查询功能。随着信息技术的不断发展,数据库已经成为现代计…...
)
周末总结(2024/03/30)
工作 接受破烂现状,改变状态 上周一周的工作都感觉是摸鱼状态,每天只有三个小时左右的时间聚焦在工作上,其他时间都在胡思乱想。但是我发现可以在工作中学习和下班相关的技术栈。我无意改变自己的工作状态,只想在5月底找好下家然后…...
爬楼梯)
(75)爬楼梯
文章目录 1. 每日一言2. 题目2.1 解题思路2.1.1 递归2.1.2 记忆化搜索2.1.3 动态规划2.1.4 动态规划空间优化 2.2 代码2.2.1 递归2.2.2 记忆化搜索2.2.3 动态规划2.2.4 动态规划空间优化 3. 结语 1. 每日一言 Happy life lies in a peaceful mind. 幸福的生活存在于心绪的宁静…...
ttkbootstrap界面美化系列之Notebook(四)
在简单的界面设计中,Notebook也是常用的组件之一,Notebook组件的引入可以根据标签来切换不同的界面。使得界面更有层次感,不必都挤在一个界面上。在tkinter中就有Notebook组件,在ttkbootstrap中,同样也对Notebook进行了…...

MySQL8存储过程整合springboot
注意:调用使用mybatis-plus3形式调用,可能会有些区别 1. 创建存储过程 -- -- 生成员工工号的存储过程 DELIMITER $$ CREATE PROCEDURE generate_employee_number(OUT employeeNumber VARCHAR(20)) -- 解释 out 一个返回值 BEGINDECLARE prefix VARCHAR…...

Acwing 1238.日志统计 双指针
小明维护着一个程序员论坛。现在他收集了一份”点赞”日志,日志共有 N� 行。 其中每一行的格式是: ts id 表示在 ts 时刻编号 id 的帖子收到一个”赞”。 现在小明想统计有哪些帖子曾经是”热帖”。 如果一个帖子曾在任意一个长度为 D 的…...

Matlab-R2022b-安装文件分享
一、MATLAB主要特点和功能 MATLAB是一款强大的科学计算软件,专门用于算法开发、数据分析、数值计算以及科学数据可视化。 以下是一些MATLAB的主要特点和功能: 1.矩阵运算: MATLAB的名字来源于"Matrix Laboratory"(矩阵实验室&…...

Flutter开发之objectbox
Flutter开发之objectbox 在之前进行iOS开发的时候使用WCDB去进行管理数据库很方便,它支持ORM(Object-Relational Mapping,对象关系映射),用于实现面向对象编程语言里不同类型系统的数据之间的转换。 那么在Flutter开发…...
)
AI Drug Discovery Design(学习路线)
AIDD,即AI Drug Discovery & Design,是近年来非常火热的技术应用,已经介入到新药设计到研发的大部分环节当中,为新药发现与开发带来了极大的助力。其学习路线涉及多个学科和领域的知识。以下是一个可能的AIDD学习路线…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
