神经网络与深度学习(一)
线性回归
定义
- 利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法
要素
- 训练集(训练数据)
- 输出数据
- 拟合函数
- 数据条目数
场景
- 预测价格(房屋、股票等)、预测住院时间(针对住院病人等)、预测需求(零售销量等)
实例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics# 创建一些随机的线性数据
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 + 3 * x + np.random.rand(100, 1)# 将数据分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)# 创建线性回归模型
regressor = LinearRegression() # 使用训练数据来训练模型
regressor.fit(x_train, y_train) # 使用测试数据来评估模型
y_pred = regressor.predict(x_test)# 计算模型的准确度
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))# 绘制原始数据和拟合的直线
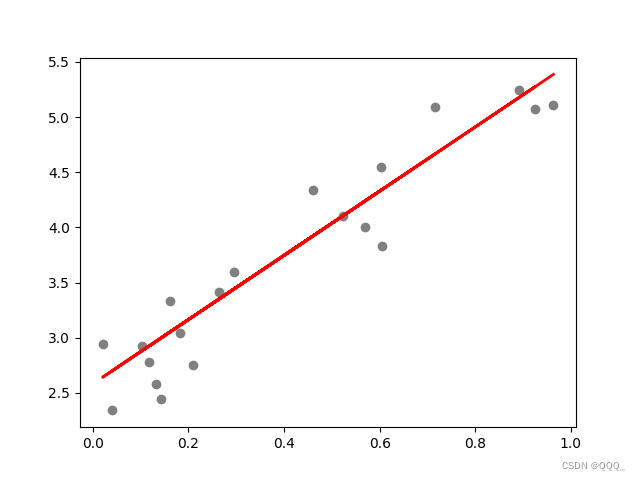
plt.scatter(x_test, y_test, color='gray')
plt.plot(x_test, y_pred, color='red', linewidth=2)
plt.show()
分类与回归
线性二分类
定义
线性分类器则透过特征的线性组合来做出分类决定,以达到此种目的。简言之,样本通过直线(或超平面)可分。
- 线性分类器输入:特征向量
- 输出:哪一类。如果是二分类问题,则为0和1,或者是属于某类的
- 概率:即0-1之间的数。
线性分类与线性回归差别
- 输出意义不同:属于某类的概率VS回归具体值
- 参数意义不同:最佳分类直线VS最佳拟合直线
- 维度不同:一维的回归VS二维的分类
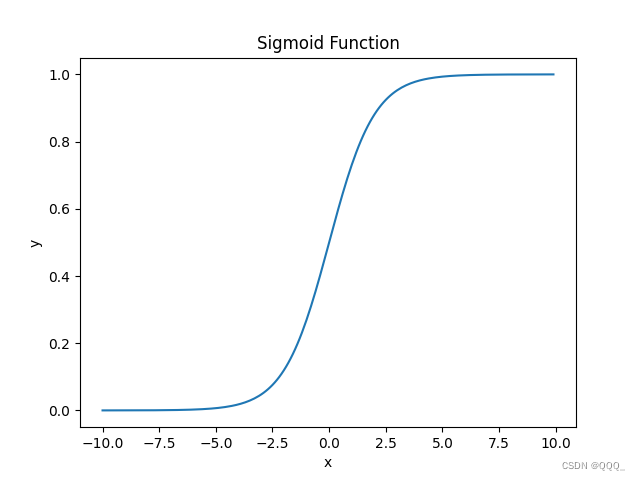
Sigmoid函数
- 用于结果转换,归入0-1区间
梯度下降法
- 梯度下降法(Gradient Descent)是一种用于找到函数局部极小值的优化算法。它通过向函数上当前点对应梯度的反方向迭代搜索,以寻找最小值。如果相反地向梯度正方向迭代搜索,则会接近函数的局部极大值点,这个过程被称为梯度上升法。
二分类实例
import numpy as np
import matplotlib.pyplot as plt# 设定随机种子以便结果可复现
np.random.seed(0)# 生成数据集
X = np.random.randn(100, 2) # 生成100个样本,每个样本有2个特征
Y = np.where(X[:, 0] + X[:, 1] > 0, 1, 0) # 根据线性方程生成标签# 绘制原始数据
plt.scatter(X[Y == 0][:, 0], X[Y == 0][:, 1], color='red', label='Class 0')
plt.scatter(X[Y == 1][:, 0], X[Y == 1][:, 1], color='blue', label='Class 1')
plt.legend()
plt.title('Original Data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()# 梯度下降函数
def gradient_descent(X, Y, theta, alpha, iterations):m = len(X)for i in range(iterations):h = np.dot(X, theta)loss = h - Ygradient = np.dot(X.transpose(), loss) / mtheta = theta - alpha * gradientreturn theta# 初始化参数
theta = np.zeros(2) # 特征数量 + 截距项
alpha = 0.01 # 学习率
iterations = 1000 # 迭代次数# 运行梯度下降
theta = gradient_descent(X, Y, theta, alpha, iterations)# 绘制决策边界
def plot_decision_boundary(theta, X, Y):x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1h = (theta[0] * x_min + theta[1] * y_min) / -theta[2]k = -theta[0] / theta[1]xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))Z = np.dot(np.array([xx.ravel(), yy.ravel()]), theta)Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)plt.scatter(X[Y == 0][:, 0], X[Y == 0][:, 1], color='red', label='Class 0')plt.scatter(X[Y == 1][:, 0], X[Y == 1][:, 1], color='blue', label='Class 1')plt.legend()plt.title('Decision Boundary')plt.xlabel('X1')plt.ylabel('X2')plot_decision_boundary(theta, X, Y)
plt.show()

指数回归
实例
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit# 定义指数函数
def exponential_func(x, a, b, c):return a * np.exp(b * x) + c# 创建模拟数据
x = np.linspace(0, 4, 50)
y = 3 * np.exp(2.5 * x) + 0.5
np.random.seed(1729)
yn = y + 0.2 * np.random.normal(size=len(x))# 使用curve_fit进行拟合
popt, pcov = curve_fit(exponential_func, x, yn)# 输出最优参数
print("最优参数: ", popt)# 使用最优参数进行预测
y_pred = exponential_func(x, *popt)# 绘制原始数据和拟合曲线
plt.figure(figsize=(8, 6))
plt.scatter(x, yn, label='原始数据')
plt.plot(x, y_pred, 'r-', label='拟合曲线')
plt.legend()
plt.show()

多分类回归
- 多分类回归通常指的是多目标回归问题,即预测多个连续的输出变量。与多分类分类问题不同,回归任务预测的是连续的数值,而不是离散的类别。
实例
- 二分类
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler# 创建模拟的二分类数据集
np.random.seed(0)
X = np.random.randn(100, 2) # 生成100个二维数据点
y = (X[:, 0] + X[:, 1] > 0).astype(int) # 创建简单的线性分类标签# 使用逻辑回归(其输出层实际上应用了Softmax对于二分类)
# 对于多分类问题,我们可以使用LogisticRegression(multi_class='multinomial', solver='lbfgs')
clf = LogisticRegression(multi_class='multinomial', solver='lbfgs')
clf.fit(X, y)# 预测概率
probabilities = clf.predict_proba(X)# 绘制散点图
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k')# 绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
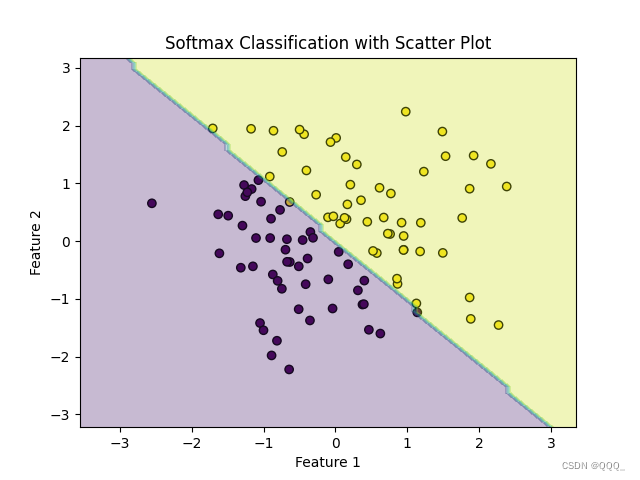
plt.contourf(xx, yy, Z, alpha=0.3, cmap='viridis')plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Softmax Classification with Scatter Plot')
plt.show()
- 多分类
import numpy as np
import matplotlib.pyplot as plt# 设置随机种子以保证结果的可复现性
np.random.seed(0)# 定义类别数量和每个类别的数据点数量
num_classes =5
num_points_per_class = 5000# 生成随机散点数据
X = np.zeros((num_classes * num_points_per_class, 2))
for i in range(num_classes):# 为每个类别生成一个正态分布的簇X[i * num_points_per_class: (i + 1) * num_points_per_class] = np.random.randn(num_points_per_class, 2) + [i, i]# 为每个类别创建一个权重向量和偏置项
W = np.random.randn(num_classes, 2)
b = np.random.randn(num_classes)# 计算每个数据点的分数
scores = np.dot(X, W.T) + b# 应用Softmax函数得到概率分布
def softmax(x):exps = np.exp(x - np.max(x, axis=1, keepdims=True))return exps / np.sum(exps, axis=1, keepdims=True)probabilities = softmax(scores)# 绘制散点图
colors = ['r', 'g', 'b', 'c', 'm'] # 每个类别的颜色
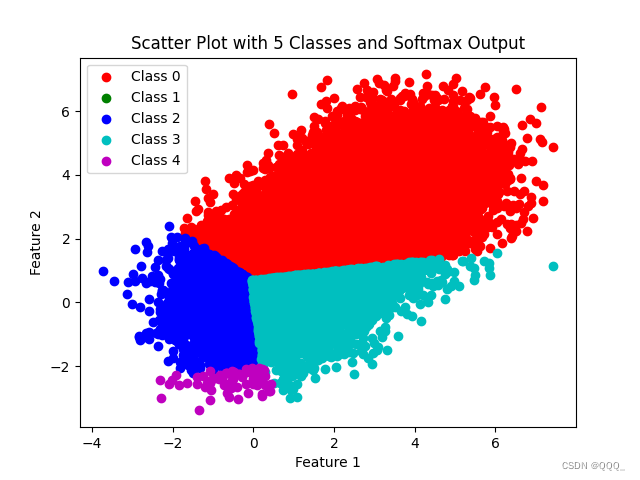
for i in range(num_classes):plt.scatter(X[scores[:, i] == np.max(scores, axis=1)][:, 0],X[scores[:, i] == np.max(scores, axis=1)][:, 1],c=colors[i], label=f'Class {i}')# 添加图例和坐标轴标签
plt.legend()
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Scatter Plot with 5 Classes and Softmax Output')# 显示图像
plt.show()# 打印Softmax概率(仅打印前5个数据点的概率作为示例)
print("Softmax Probabilities (for the first 5 points):")
print(probabilities[:5])
神经元模型
分类
- 生物神经元
- Spiking模型
- Integrate-and-fire模型
- M-P模型
- 单神经元模型
作用函数
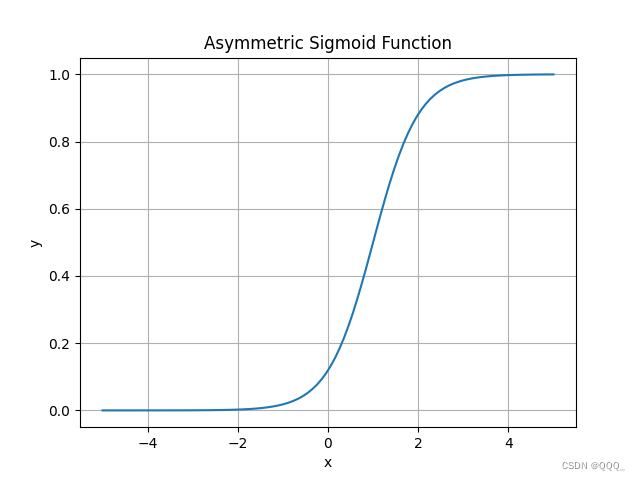
非对称型 Sigmoid 函数 (Log Sigmoid)
非对称型Sigmoid函数(也称作Log Sigmoid函数)是Sigmoid函数的一个变体,它可以将任何实数映射到介于0和1之间的值,但不像标准的Sigmoid函数那样是对称的。非对称型Sigmoid函数通常具有不同的形状参数,允许用户调整函数的形状以满足特定的需求。非对称型Sigmoid函数的一般形式可以表示为:f(x) = 1 / (1 + exp(-a * (x - b)))其中,a和b是形状参数。a控制函数的斜率,而b控制函数的中心位置。当a为正数时,函数在x=b处呈现出一个向上的S形曲线;当a为负数时,函数在x=b处呈现出一个向下的S形曲线。通过调整a和b的值,可以改变函数的形状和位置。
对称型 Sigmoid 函数 (Tangent Sigmoid)
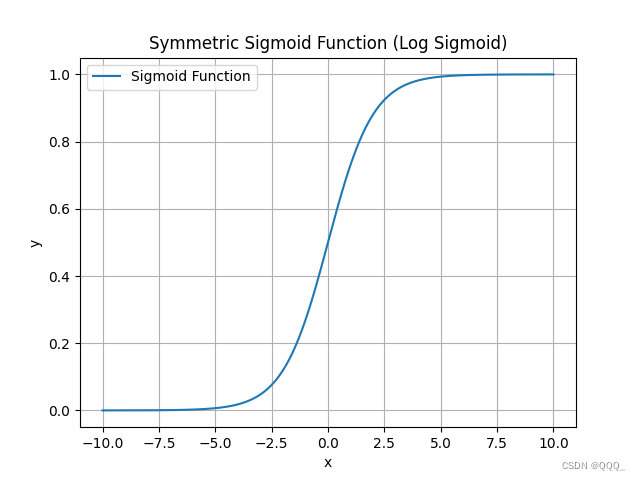
对称型 Sigmoid 函数(也称为 Logistic Sigmoid 函数)是一种常用的非线性函数,通常用于将连续值映射到 0 到 1 之间的概率值。标准的对称型 Sigmoid 函数公式如下:
f(x) = 1 / (1 + exp(-x))
其中 exp 是自然指数函数,x 是输入值。这个函数将任何实数 x 映射到 (0, 1) 区间内,其中当 x 趋近于正无穷时,f(x) 趋近于 1;当 x 趋近于负无穷时,f(x) 趋近于0。
多层感知机
应对问题
- 线性不可分问题:无法进行线性分类。Minsky 1969年提出XOR问题
- 三层感知器可识别任一凸多边形或无界的凸区域。
- 更多层感知器网络,可识别更为复杂的图形。
实现过程
- 在输入和输出层间加一或多层隐单元,构成多层感知器(多层前馈神经网络)
- 加一层隐节点(单元)为三层网络,可解决异或(XOR)问题由输入得到两个隐节点、一个输出层节点的输出。
多层前馈网络
- 多层感知机是一种多层前馈网络,由多层神经网络构成,每层网络将输出传递给下一层网络。神经元间的权值连接仅出现在相邻层之间,不出现在其他位置。如果每一个神经元都连接到上一层的所有神经元(除输入层外),则成为全连接网络。
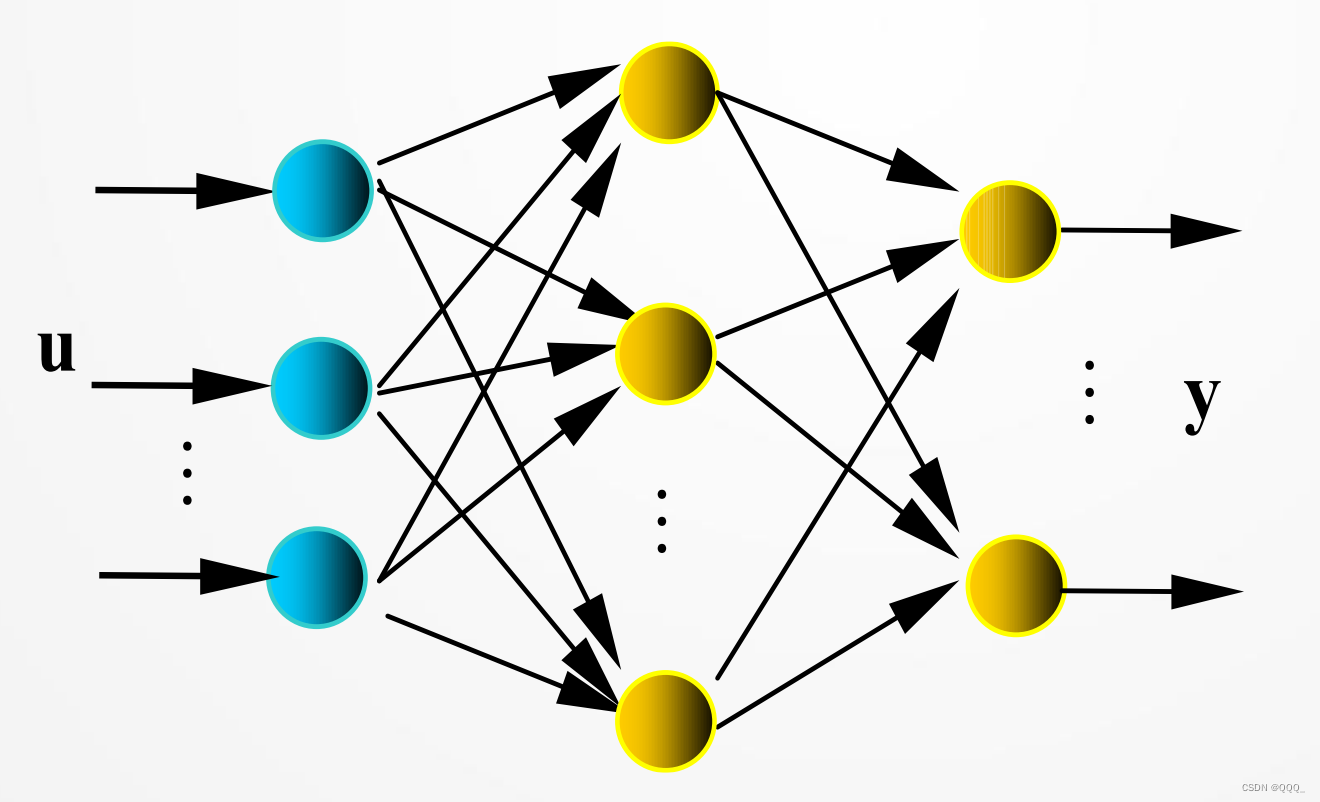
BP网络
- 多层前馈网络的反向传播 (BP)学习算法,简称BP算法,是有导师的学习,它是梯度下降法在多层前馈网中的应用。
网络结构:见图,𝐮(或𝐱 )、𝐲是网络的输入、输出向量,神经元用节点表示,网络由输入层、隐层和输出层节点组成,隐层可一层
,也可多层(图中是单隐层),前层至后层节点通过权联接。由于用BP学习算法,所以常称BP神经网络。
BP学习算法
由正向传播和反向传播组成:
- 正向传播是输入信号从输入层经隐层,传向输出层,若输出层得到了期望的输出,则学习算法结束;否则,转至反向传播。
- 反向传播是将误差(样本输出与网络输出之差)按原联接通路反向计算,由梯度下降法调整各层节点的权值和阈值,使误差减小。
优缺点:
- 学习完全自主
- 可逼近任意非线性函数
- 算法非全局收敛
- 收敛速度慢
- 学习速率α选择
- 神经网络如何设计(几层?节点数?)
性能优化
常用技巧
- 模型初始化
- 训练数据与测试数据
- 训练数据与测试数据:𝐾折交叉验证
- 欠拟合与过拟合
- 权重衰减 (𝐿2正则化)
- Dropout(暂退)
动量法
自适应梯度法
相关文章:

神经网络与深度学习(一)
线性回归 定义 利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法 要素 训练集(训练数据)输出数据拟合函数数据条目数 场景 预测价格(房屋、股票等)、预测住院时间&#…...
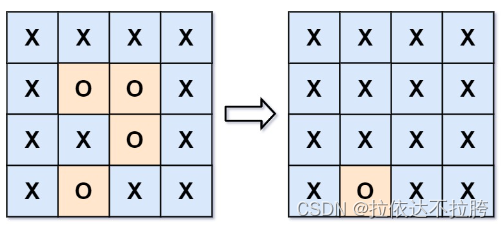
算法学习——LeetCode力扣图论篇2
算法学习——LeetCode力扣图论篇2 1020. 飞地的数量 1020. 飞地的数量 - 力扣(LeetCode) 描述 给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。 一次 移动 是指从一个陆地单元格走到另一个相…...
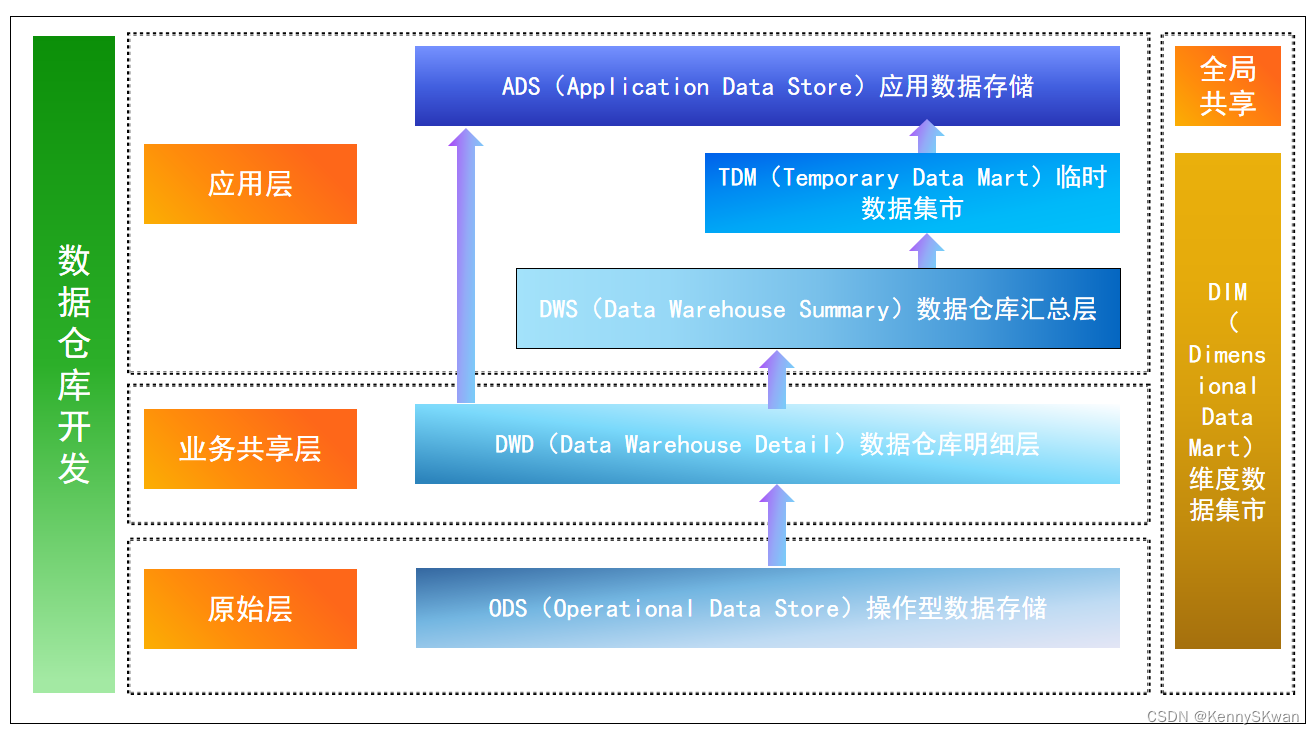
大数据设计为何要分层,行业常规设计会有几层数据
大数据设计通常采用分层结构的原因是为了提高数据管理的效率、降低系统复杂度、增强数据质量和可维护性。这种分层结构能够将数据按照不同的处理和应用需求进行分类和管理,从而更好地满足不同层次的数据处理和分析需求。行业常规设计中,数据通常按照以下…...

css3之2D转换transform
2D转换transform 一.移动(translate)(中间用,隔开)二.旋转(rotate)(有单位deg)1.概念2.注意点3.转换中心点(transform-origin)(中间用空格)4.一些例子(css三角和旋转) 三…...

pytest中文使用文档----6临时目录和文件
1. 相关的fixture 1.1. tmp_path1.2. tmp_path_factory1.3. tmpdir1.4. tmpdir_factory1.5. 区别 2. 默认的基本临时目录 1. 相关的fixture 1.1. tmp_path tmp_path是一个用例级别的fixture,其作用是返回一个唯一的临时目录对象(pathlib.Path…...
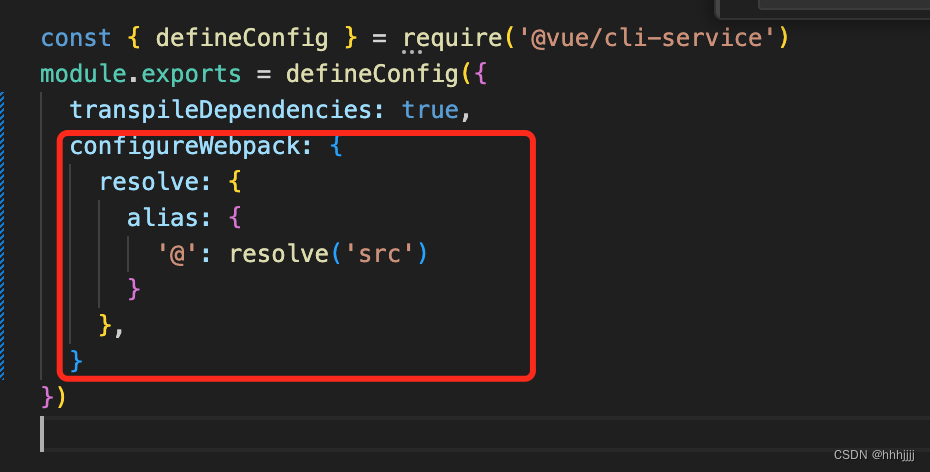
从0开始搭建基于VUE的前端项目
准备与版本 安装nodejs(v20.11.1)安装vue脚手架(vue/cli 5.0.8) ,参考(https://cli.vuejs.org/zh/)vue版本(2.7.16),vue2的最后一个版本 初始化项目 创建一个git项目(可以去gitee/github上创建ÿ…...
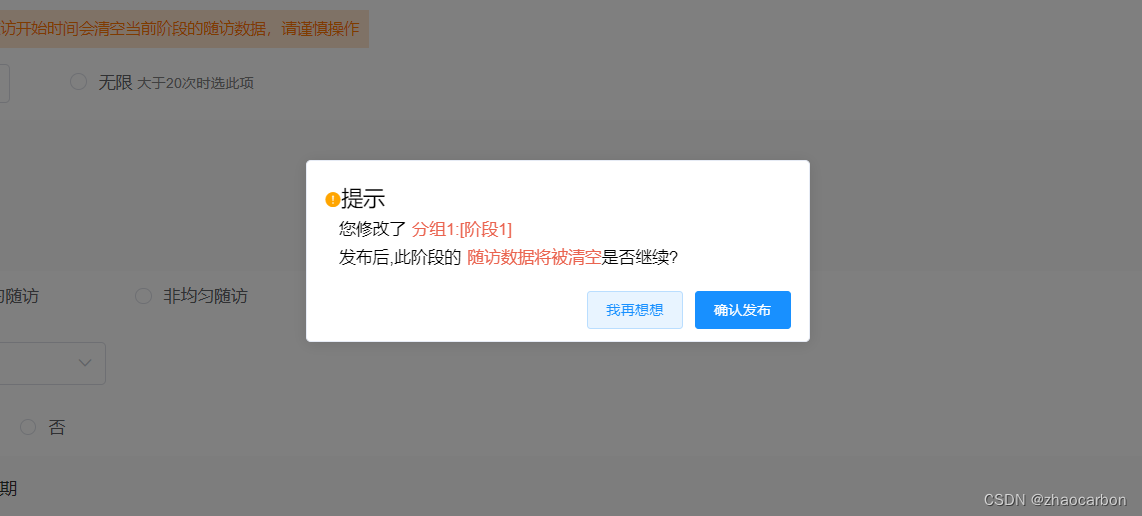
elementUI this.$msgbox msgBox自定义 样式自定义 富文本
看这个效果是不是很炫?突出重点提示内容,对于用户交互相当的棒! 下来说说具体实现: let self = this const h = self.$createElement; this.$msgbox({title: null,message: h("p", {style: "margin-top:10px"}, [h("i", {class: "el-i…...

Lua与Python区别
Lua和Python都是流行的编程语言,但它们在设计哲学、应用领域和性能特点上有所不同。以下是Lua和Python之间的对比: 1. **设计哲学**: - Lua被设计为一个轻量级的嵌入式脚本语言,重点在于简单性和效率。它有一个小巧的标准库,通…...
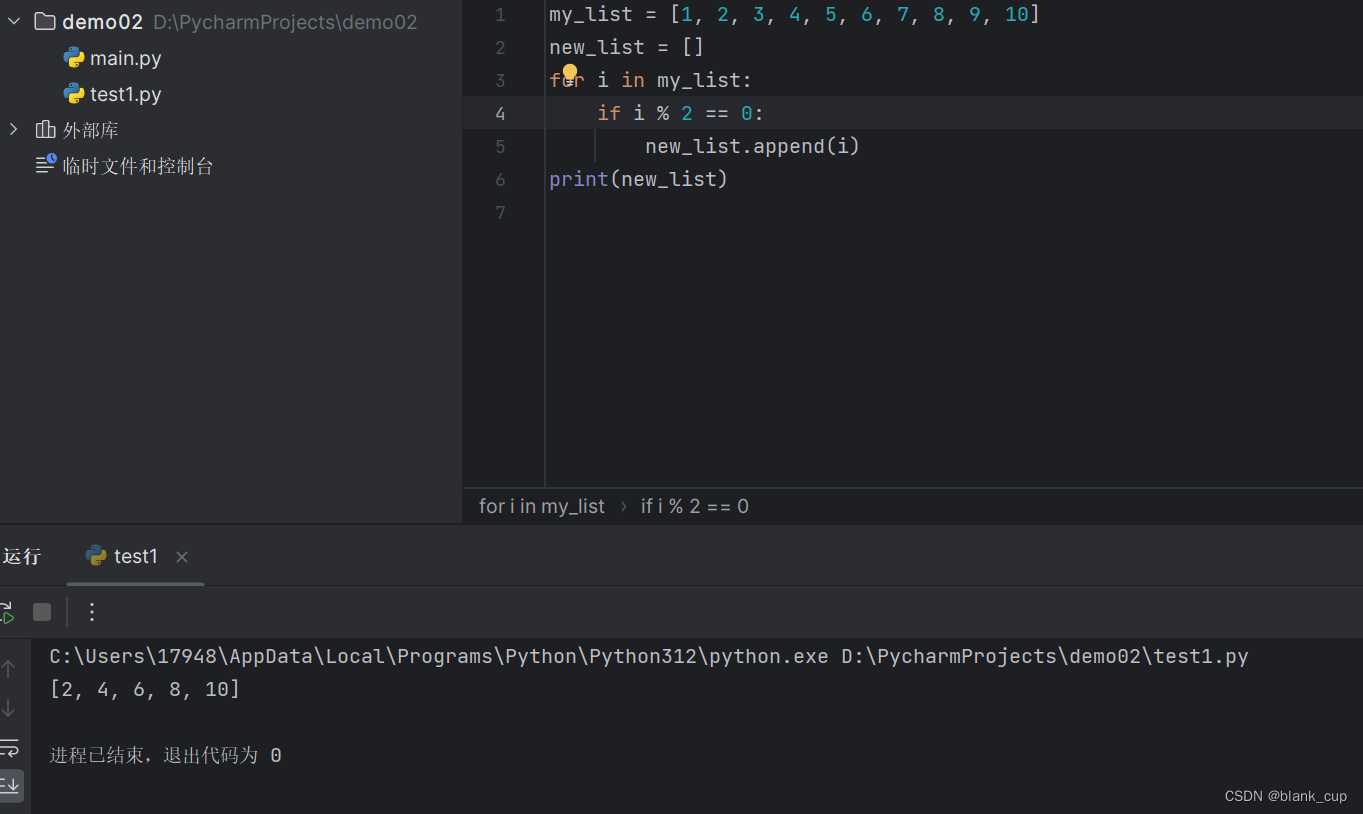
Python学习(二)
数据容器 数据容器根据特点的不同,如: 是否支持重复元素是否可以修改是否有序,等 分为5类,分别是: 列表(list)、元组(tuple)、字符串(str)、集…...
管理阿里云服务器ECS -- 网站选型和搭建
小云:我已经学会了如何登录云服务器ECS了,但是要如何搭建网站呢? 老王:目前有很多的个人网站系统软件,其中 WordPress 是使用非常广泛的一款,而且也可以把 WordPress 当作一个内容管理系统(CMS…...
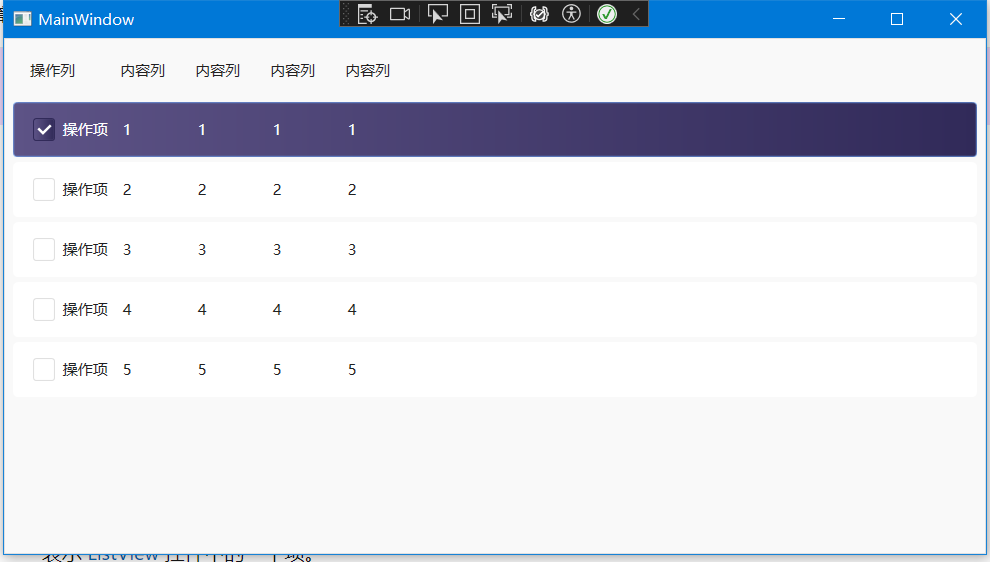
WPF中继承ItemsControl子类控件数据模板获取选中属性
需求场景 列表类控件,如 ListBox、ListView、DataGrid等。显示的行数据中,部分内容依靠选中时触发控制,例如选中行时行记录复选,部分列内容控制显隐。 案例源码以ListView 为例。 Xaml 部分 <ListView ItemsSource"{Bi…...
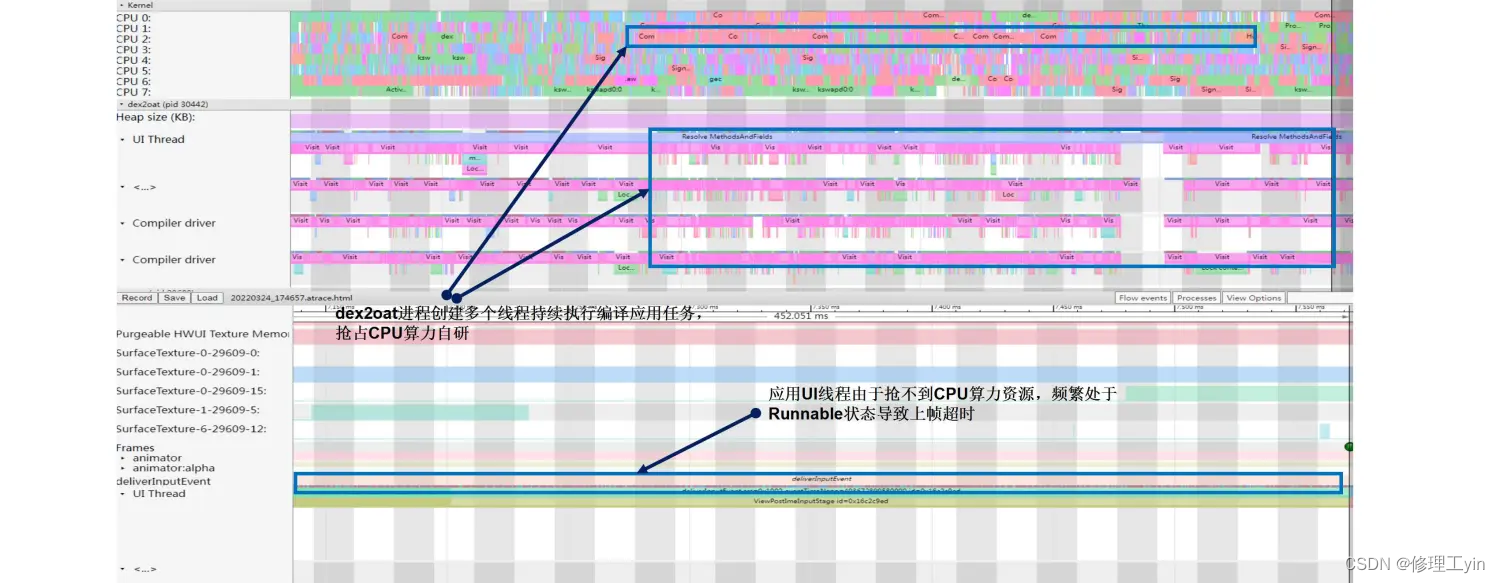
Android卡顿掉帧问题分析之实战篇
本文将结合典型实战案例,分析常见的造成卡顿等性能问题的原因。从系统工程师的总体角度来看 ,造成卡顿等性能问题的原因总体上大致分为三个大类:一类是流程执行异常;二是系统负载异常;三是编译问题引起。 1 流程执行异…...
OpenKylin安装Kafka
一、操作系统 openKylin 1.0.1 X86 二、下载安装包 # 安装依赖jdk sudo apt-get update sudo apt-get install default-jdk # 下载kafka mkdir -p /data/software/kafka wget https://archive.apache.org/dist/kafka/2.4.1/kafka_2.13-2.4.1.tgz三、解压安装 # 解压缩Kafka…...

嵌入式硬件中常见的面试问题与实现
1 01 请列举您知道的电阻、电容、电感品牌(最好包括国内、国外品牌) ▶电阻 美国:AVX、VISHAY威世 日本:KOA兴亚、Kyocera京瓷、muRata村田、Panasonic松下、ROHM罗姆、susumu、TDK 台湾:LIZ丽智、PHYCOM飞元、RALEC旺诠、ROYALOHM厚生、SUPEROHM美隆、TA-I大毅、TMT…...
【Node.JS】koa
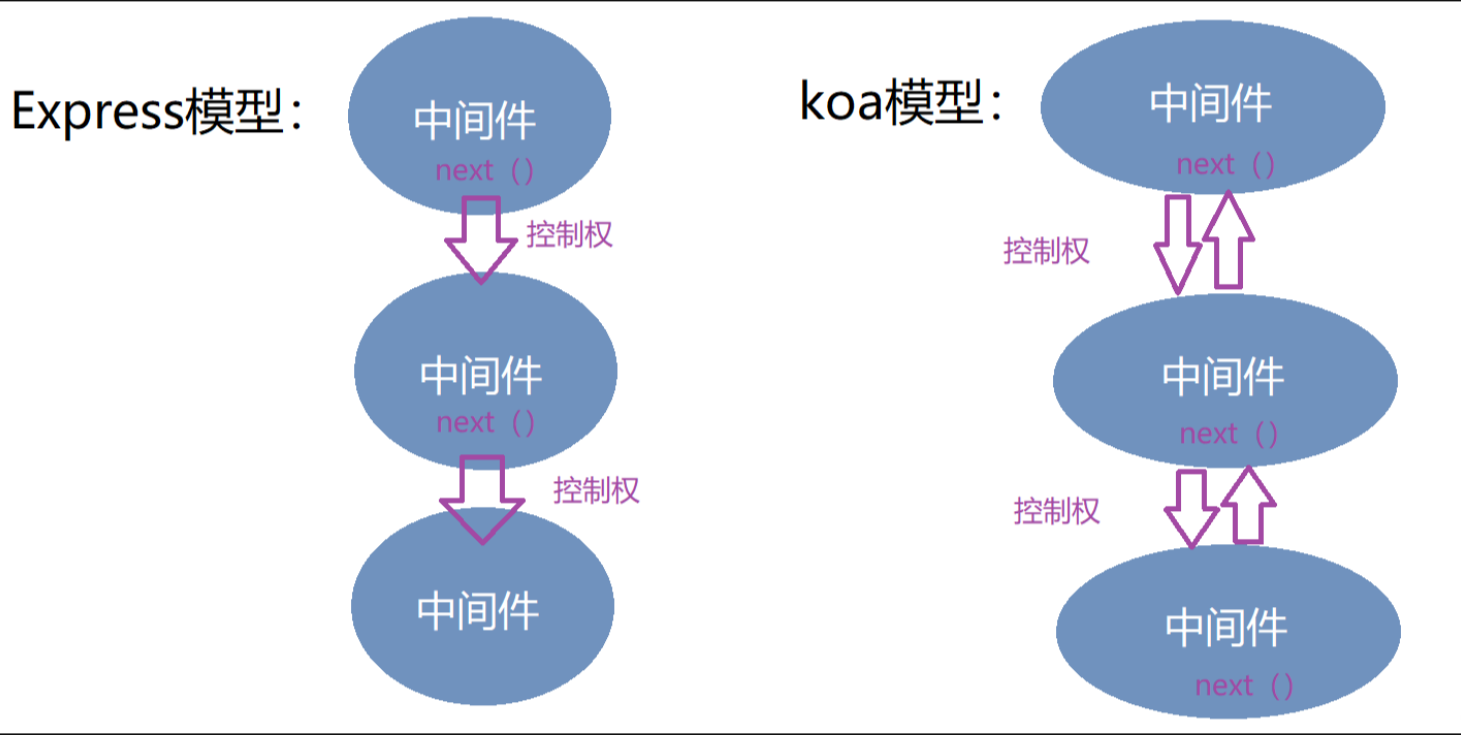
文章目录 概述koa和express对比koa下载安装使用1.创建koa项目文件目录2. 创建koa服务3. 添加路由 koa-router4. 数据库服务 mongodb5. 添加请求参数json处理 koa-bodyparser6. 用户接口举例7.引入koa一些常用插件8.用户登录验证 koa-jwt9.webpack生产打包 来源 概述 Koa 是一个…...

工作日志- 不定期更新
1. protobuf中使用import引用其他proto文件,生成后在go语言的go modules中import 包名报错问题。 public.proto文件 //protoc --go_outpluginsgrpc:. public.proto syntax "proto3";package public;option go_package "self/game-service/msg/pu…...

Qt使用opencv打开摄像头
1.效果图 2.代码 #include "widget.h"#include <QApplication>#include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/imgproc/imgproc.hpp>#include <QImage> #include <QLabel> #incl…...

Redis的Hash数据结构中100万对field和value,field是自增时如何优化?优化Hash结构。
ZipList使用是有条件的,当entry数据量太大时就会启用哈希结构,占用内存空间 1.设置bigkey的上限 在redis.config中设置 2.拆分为string类型 String底层结果没有太多优化,占用内存多 想要批量获取数据麻烦 3.拆分为小的hash 将id/100作为…...
二十四种设计模式与六大设计原则(一):【策略模式、代理模式、单例模式、多例模式、工厂方法模式、抽象工厂模式】的定义、举例说明、核心思想、适用场景和优缺点
目录 策略模式【Strategy Pattern】 定义 举例说明 核心思想 适用场景 优缺点 代理模式【Proxy Pattern】 定义 举例说明 核心思想 适用场景 优缺点 单例模式【Singleton Pattern】 定义 举例说明 核心思想 适用场景 优缺点 多例模式【Multition Pattern】…...

mac怎么删除python
mac 默认安装了python2;自己后面又安装了python3;为了方便,现在想将python3换成Anaconda3。 Anaconda是一个开源的Python发行版本,其包含了conda、Python等180多个科学包及其依赖项。 Python3安装之后,在系统中不同目…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
