parallel linux虚拟机没有root权限
前言
今天刚在parallel上装上linux虚拟机,安装的是Debian发行版。用终端输入命令时,无意间发现当前用户竟然不是root用户,岂有此理!众所周知,Linux系统一般安装之后都是默认root用户的,但是可能parallel先配置好了一些系统设置,导致用户的默认权限不是root权限。当然,不用着急,方法还是有的。
解决方法

图中列举了5个步骤,按照步骤来就可以解决。(由于笔者使用的是Debian版本的Linux,其他版本为测试过,因此不一定适用)。图中我们可以看见,默认的是用户名是parallel,这也正说明了parallel在安装Linux系统是是提前设定好了一些系统设置的,就比如说这个用户名为parallel。
后续步骤
新建窗口
当你点击终端左上角的“➕”新建终端窗口时,会发现新建窗口的当前用户又变成了parallel,这时该怎么办呢?很简单,由于你刚才已经设定过了管理员权限,所以只需再次执行step 4和step 5就行了。即
su -
password:password就是你刚才设定的新密码。
当你退出系统后,重新log in,也只需要执行上面的“su -”,然后输入密码(指新的管理员密码)即可。
新建用户
引入这样一个情景,在你刚才设置好了管理员密码后,你又新建了一个用户,然后登录新的用户。这时你想在这个新的用户使用管理员权限,使用“su -”,然后再输入密码,也可以获得管理员权限。综上,我们可以得知这个获取管理员权限的操作是全局有效的。
参考
新安装的linux虚拟机发现没有注册root账户,该如何解决?~亲测有效_linux虚拟机没有root账户-CSDN博客
相关文章:

parallel linux虚拟机没有root权限
前言 今天刚在parallel上装上linux虚拟机,安装的是Debian发行版。用终端输入命令时,无意间发现当前用户竟然不是root用户,岂有此理!众所周知,Linux系统一般安装之后都是默认root用户的,但是可能parallel先…...

科技下乡:数字乡村改变乡村生活方式
在科技飞速发展的时代,数字化、信息化浪潮正以前所未有的速度席卷全球。在这场科技革命中,乡村不再是滞后的代名词,而是成为了数字乡村建设的热土。科技下乡,让数字乡村成为了改变乡村生活方式的重要力量。 一、科技下乡…...

【GitLab】Ubuntu使用宝塔安装GitLab最新社区版
首先在Ubuntu安装宝塔面板 在官网可以找到脚本一键安装 安装GitLab社区版 然后在宝塔面板的“软件商店”里面找到GitLab最新社区版 12.8.1一键安装 安装过程中可能出现以下问题: 1.卡在ruby_block[wait for logrotate service socket] action run 解决办法&…...

C++入门(2)
目录 3. C输入&输出 4. 缺省(默认)参数 4.1 缺省参数概念 4.2 缺省参数分类 全缺省参数 半缺省参数 5. 函数重载 5.1 函数重载概念 6. 引用 6.1 引用概念 6.2 引用特性 6.3 常引用 6.4 使用场景 6.5 传值、传引用效率比较 6.5.1 值和引用的作为返回值类型的性能比较 6.6 引…...
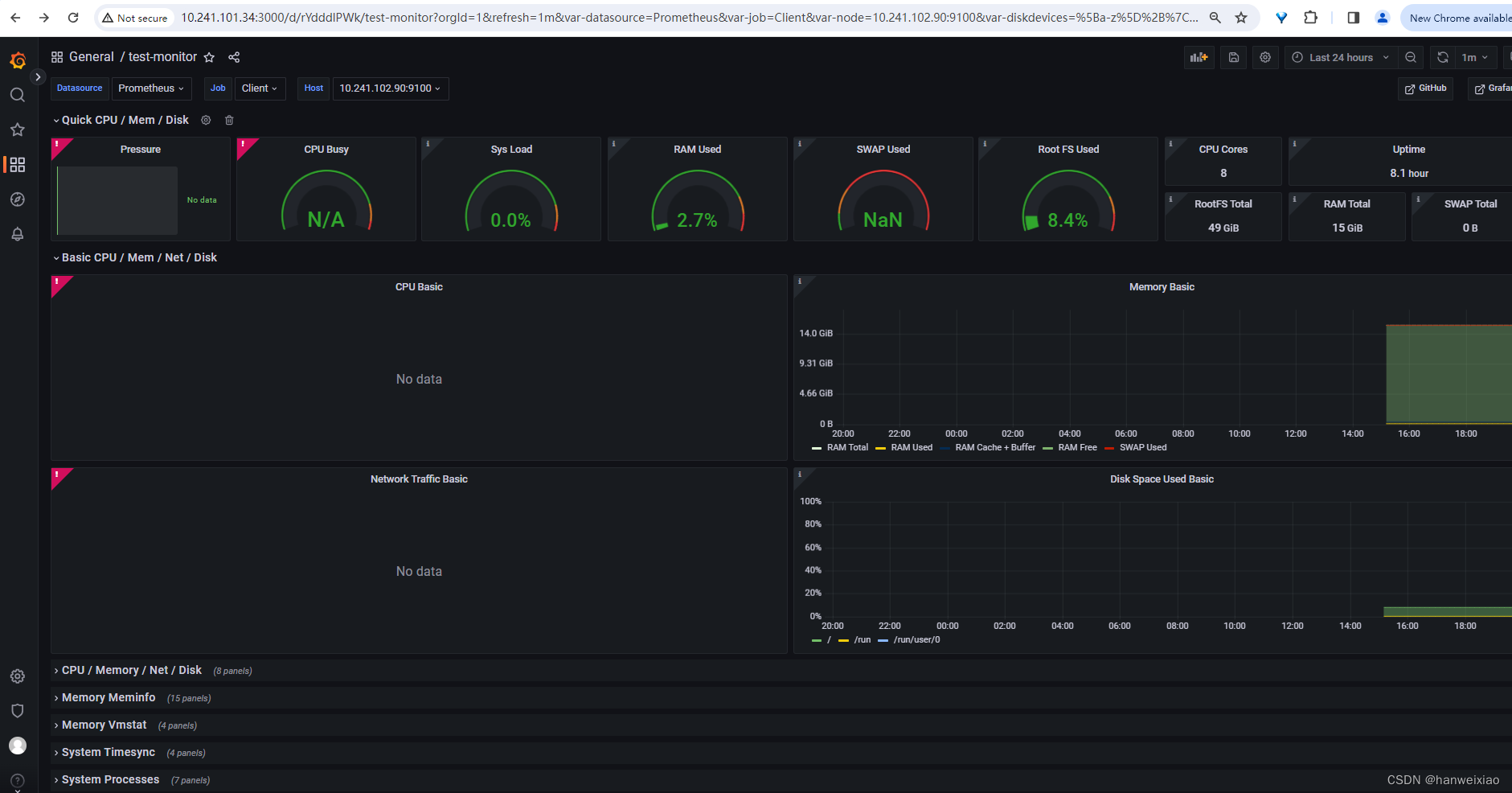
Prometheus +Grafana +node_exporter可视化监控Linux + windows虚机
1、介绍 背景:需要对多台虚机进行负载可视乎监控,并进行及时的报警 2、架构图 node_exporter :主要是负责采集服务器的信息。 Prometheus :主要是负责存储、抓取、聚合、查询方面。 Grafana : 主要是…...

腾讯云容器与Serverless的融合:探索《2023技术实践精选集》中的创新实践
腾讯云容器与Serverless的融合:探索《2023技术实践精选集》中的创新实践 文章目录 腾讯云容器与Serverless的融合:探索《2023技术实践精选集》中的创新实践引言《2023腾讯云容器和函数计算技术实践精选集》整体评价特色亮点分析Serverless与Kubernetes的…...

python 字典练习
def main():dict1{姓名:张三, 工资: 5000}dict2{姓名:李四, 工资: 6600}dict3{姓名:王五, 工资: 8500}dict4{}dict1.update(dict2)#字典的写法print(dict1)dict1.setdefault("3月",0)#存在不作为,不存在则增补print(dict1)names[]list[dict1,dict2,dict3]…...

Postman进阶功能实战演练
Postman除了前面介绍的一些功能,还有其他一些小功能在日常接口测试或许用得上。今天,我们就来盘点一下,如下所示: 1.数据驱动 想要批量执行接口用例,我们一般会将对应的接口用例放在同一个Collection中,然…...

Flink基于Hudi维表Join缺陷解析及解决方案
Hudi,这个近年来备受瞩目的数据存储解决方案,无疑是大数据领域的一颗耀眼新星。其凭借出色的性能和稳定性,以及对于数据湖场景的深度适配,赢得了众多企业和开发者的青睐。然而,正如任何一项新兴技术,Hudi在…...

3.31学习总结
(本次学习总结,总结了目前学习java遇到的一些关键字和零碎知识点) 一.static关键字 static可以用来修饰类的成员方法、类的成员变量、类中的内部类(以及用static修饰的内部类中的变量、方法、内部类),另外可以编写static代码块来优化程序性…...
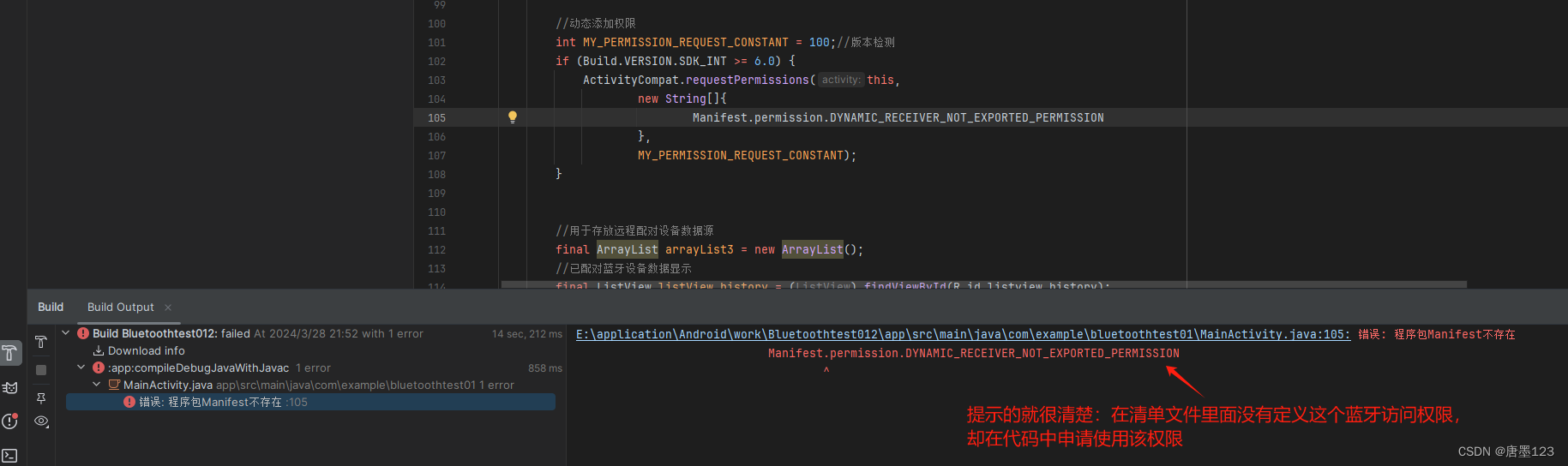
Android Studio控制台输出中文乱码问题
控制台乱码现象 安卓在调试阶段,需要查看app运行时的输出信息、出错提示信息。 乱码,会极大的阻碍开发者前进的信心,不能及时的根据提示信息定位问题,因此我们需要查看没有乱码的打印信息。 解决步骤: step1: 找到st…...
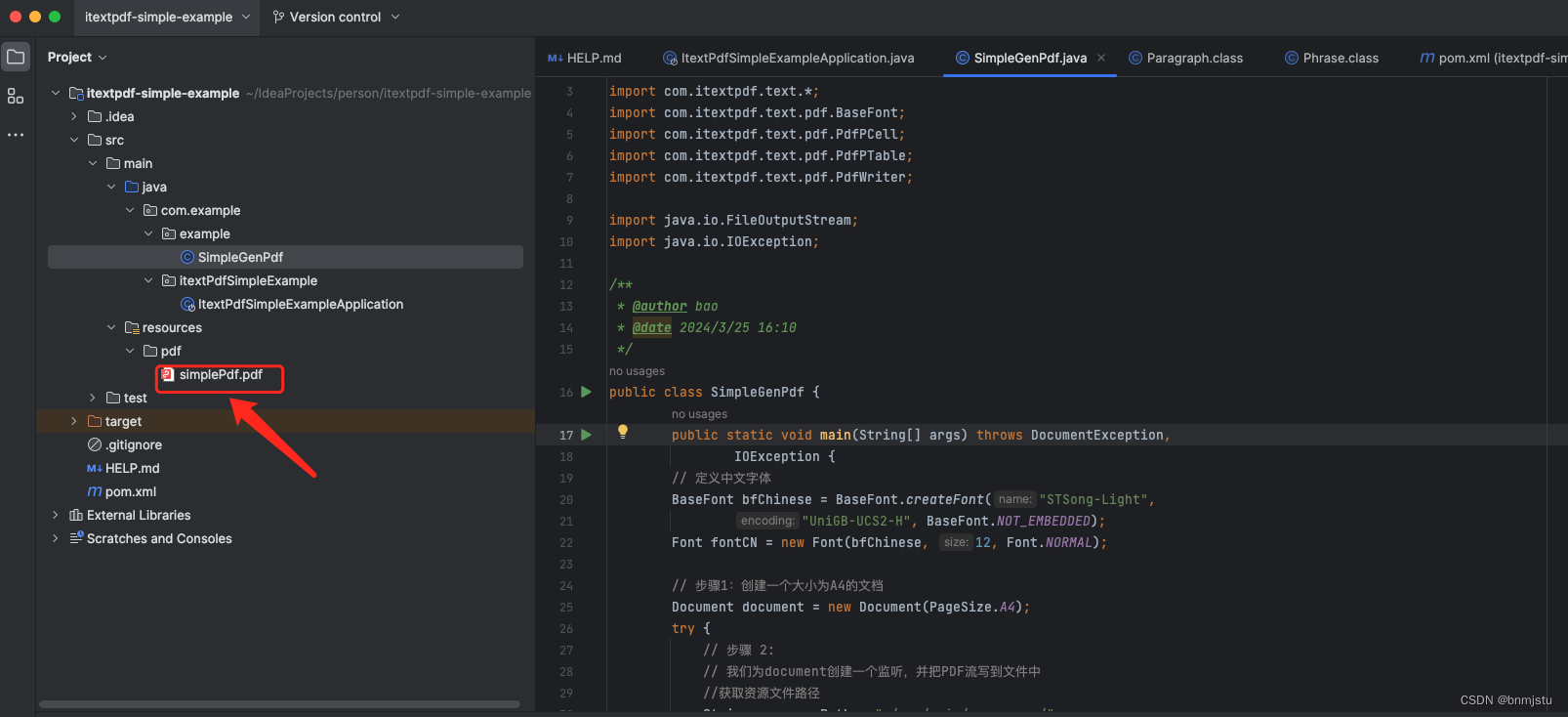
itextPdf生成pdf简单示例
文章环境 jdk1.8,springboot2.6.13 POM依赖 <dependency><groupId>com.itextpdf</groupId><artifactId>itextpdf</artifactId><version>5.5.13</version></dependency><dependency><groupId>com.ite…...

【Linux系列】tree和find命令
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

AI预测福彩3D第23弹【2024年4月1日预测--第4套算法重新开始计算第9次测试】
今天继续对第4套算法进行测试,因为第4套算法已连续多期命中,相对来说还算稳定。好了,废话不多说了,直接上预测的结果吧~ 2024年4月1日福彩3D的七码预测结果如下 第一套: 百位:0 1 …...
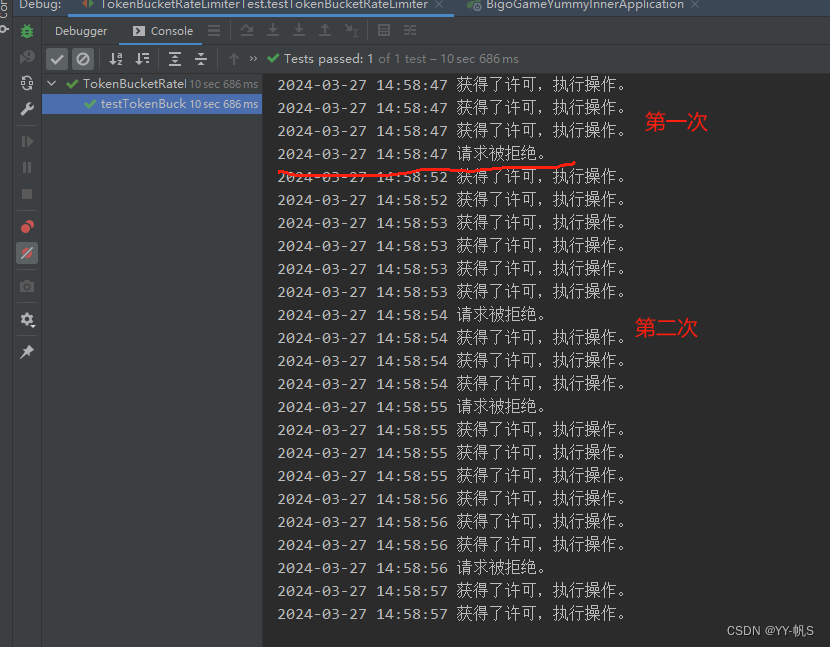
Java常见限流用法介绍和实现
目录 一、现象 二、工具 1、AtomicInteger,AtomicLong 原子类操作 2、RedisLua 3、Google Guava的RateLimiter 1) 使用 2) Demo 3) 优化demo 4、阿里开源的Sentinel 三、算法 1、计数限流 &…...
)
算法——图论:判断二分图(染色问题)
题目:. - 力扣(LeetCode) 方法一:并查集 class Solution { public:vector<int>father;int find(int x){if (father[x] ! x)father[x] find(father[x]);return father[x];}void add(int x1, int x2){int fa1 find(x1), f…...

三步提升IEDA下载速度——修改IDEA中镜像地址
找到IDEA的本地安装地址 D:\tool\IntelliJ IDEA 2022.2.4\plugins\maven\lib\maven3\conf 搜索阿里云maven仓库 复制https://developer.aliyun.com/mvn/guide中红框部分代码 这里也是一样的: <mirror><id>aliyunmaven</id><mirrorOf>*&…...

CentOS7 RPM升级支持BBR TCP/CC的内核版本
列出安装的内核 rpm -qa kernel # yum list installed kernel 删除已安装内核 sudo dnf remove kernel-4.0.4-301.fc22.x86_64 安装内核 rpm --import https://www.elrepo.org/RPM-GPG-KEY-elrepo.org rpm -Uvh http://www.elrepo.org/elrepo-release-7.0-2.el7.elrepo.noar…...

文本向量模型BGE与BGE-M3
BGE模型 BGE模型对应的技术报告为《C-Pack: Packaged Resources To Advance General Chinese Embedding》 训练数据 为了训练BGE向量模型,构建了C-MTP数据集,它包括了用来训练文本向量的文本对数据(问答对、两个同义句子、相同主题的两个文…...
【黑马头条】-day04自媒体文章审核-阿里云接口-敏感词分析DFA-图像识别OCR-异步调用MQ
文章目录 day4学习内容自媒体文章自动审核今日内容 1 自媒体文章自动审核1.1 审核流程1.2 内容安全第三方接口1.3 引入阿里云内容安全接口1.3.1 添加依赖1.3.2 导入aliyun模块1.3.3 注入Bean测试 2 app端文章保存接口2.1 表结构说明2.2 分布式id2.2.1 分布式id-技术选型2.2.2 雪…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
