【数据结构】优先级队列——堆

🧧🧧🧧🧧🧧个人主页🎈🎈🎈🎈🎈
🧧🧧🧧🧧🧧数据结构专栏🎈🎈🎈🎈🎈
🧧🧧🧧🧧🧧【数据结构】非线性结构——二叉树🎈🎈🎈🎈🎈
文章目录
- 1. 优先级队列
- 1.1 概念
- 2. 优先级队列的模拟实现
- 2.1 堆的概念
- 2.2 堆的存储方式
- 2.3 堆的创建
- 2.4 堆的插入与删除
- 3.常用接口介绍
- 3.1 PriorityQueue的特性
- 3.2 PriorityQueue常用接口介绍
- 4.堆的应用
- 4.1堆排序
- 4.2Top-k问题
1. 优先级队列
1.1 概念
前面介绍过队列,队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适,比如:在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话;初中那会班主任排座位时可能会让成绩好的同学先挑座位。在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
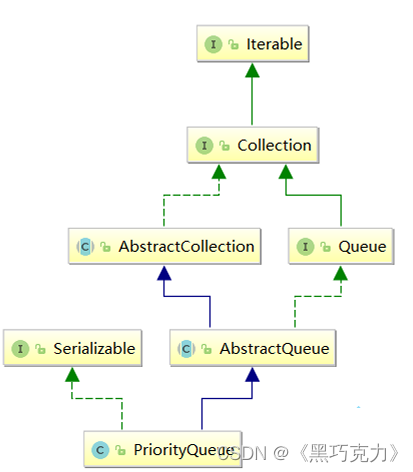
2. 优先级队列的模拟实现
JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。
2.1 堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
总结:
小根堆:父亲节点比子结点小
大根堆:父亲节点比子结点大
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
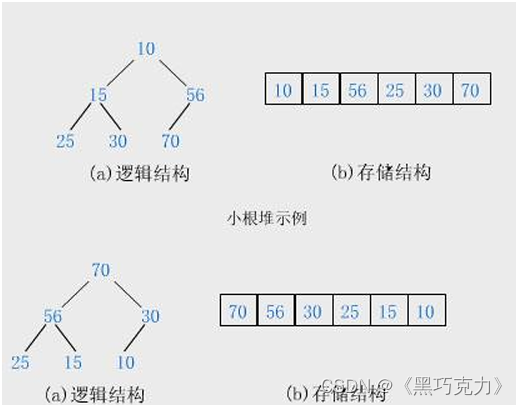
2.2 堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储,
注意:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
将元素存储到数组中后,可以根据二叉树章节的性质5对树进行还原。假设i为节点在数组中的下标,则有:
如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
2.3 堆的创建
2.3.1 堆向下调整
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,如果将其创建成堆呢?
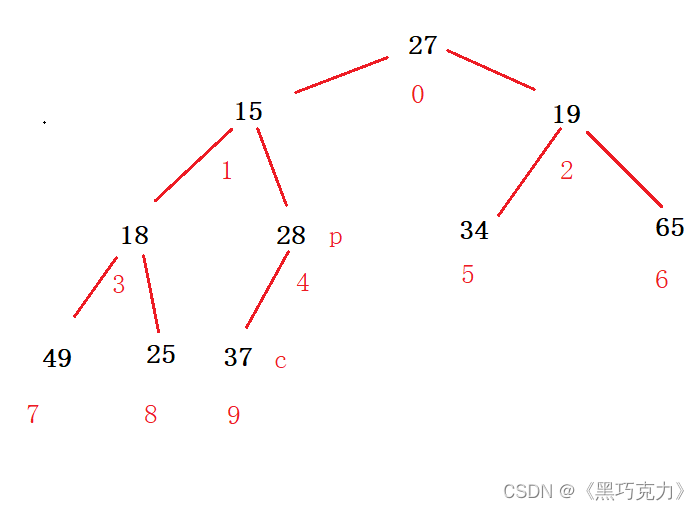
仔细观察上图后发现:根节点的左右子树已经完全满足堆的性质,因此只需将根节点向下调整好即可。
向下过程(以小堆为例):
- 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
- 如果parent的左孩子存在,即:child < size, 进行以下操作,直到parent的左孩子不存在
parent右孩子是否存在,存在找到左右孩子中最小的孩子,让child进行标
将parent与较小的孩子child比较,如果:
parent小于较小的孩子child,调整结束
否则:交换parent与较小的孩子child,交换完成之后,parent中大的元素向下移动,可能导致子
树不满足对的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续2。

代码实现:
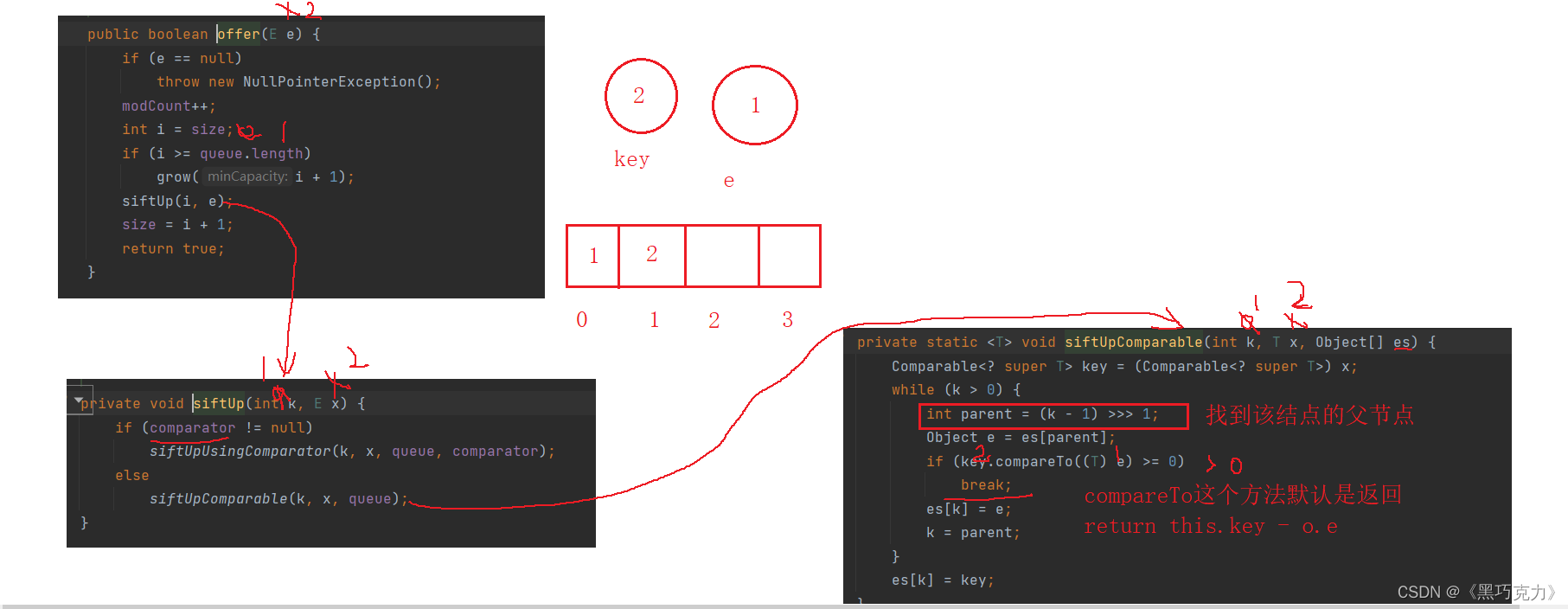
//小堆创建public void createSmallHeap() {//由最后一棵子树的结点找到它的父节点下标,然后从这棵子树开始向下调整,依次下标减1.for(int parent = (usedSize-1-1)/2;parent>=0;parent--) {//此刻传的两个参数,分别为要向下调整的根结点的下标和这个数组的长度//为什么传的数组的长度,因为这个向下调整是一个过程,它总有一个时间段是停下的,传的这个数组长度就是一个临界条件siftDown2(parent,usedSize);}}//向下调整的方法public void siftDown2(int p,int end) {//得到该结点的子结点的下标int c = 2*p + 1;//临界条件:子结点的下标<数组的长度while(c < end) {//找到最小的子结点if(c+1<end && elem[c] >elem[c+1]) {c++;}//将该结点与最小子结点比较,如大于则交换否则直接break返回if(elem[p] > elem[c]) {//交换swap(p,c);//将指向该结点的引用指向该结点的子结点,再重新将子结点的下标进行变化,检查该结点的子树是否满足大堆,不满足则继续向下调整p = c;c = 2*p + 1;} else {break;}}}
以下是创建小堆完成的图:
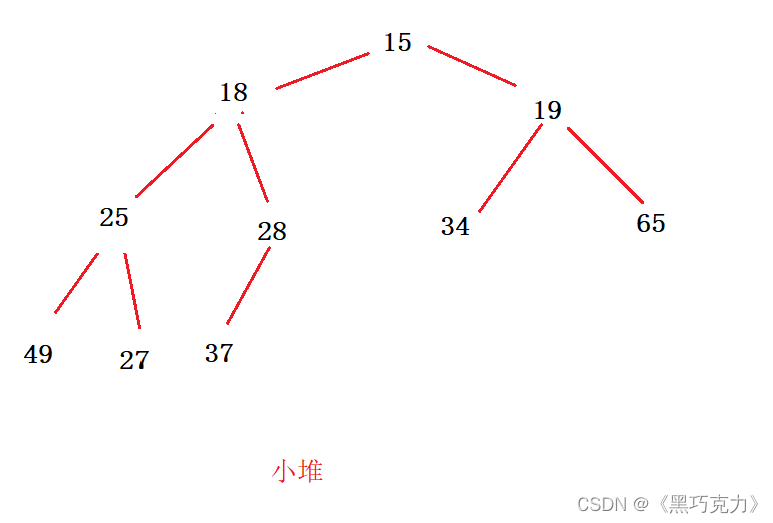
注意:在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
时间复杂度:最坏的情况是O(log2 N)是以2为底的N的对数
大堆创建的代码:
//大堆的创建public void createBigHeap() {//由最后一棵子树的结点找到它的父节点下标,然后从这棵子树开始向下调整,依次下标减1.for(int parent = (usedSize-1-1)/2;parent>=0;parent--) {//此刻传的两个参数,分别为要向下调整的根结点的下标和这个数组的长度//为什么传的数组的长度,因为这个向下调整是一个过程,它总有一个时间段是停下的,传的这个数组长度就是一个临界条件siftDown1(parent,usedSize);}}//向下调整的方法public void siftDown1(int p,int end) {//得到该结点的子结点的下标int c = 2*p + 1;//临界条件:子结点的下标<数组的长度while(c < end) {//找到最大的子结点if(c+1<end && elem[c] < elem[c+1]) {c++;}//将该结点与最大子结点比较,如小于则交换否则直接break返回if(elem[p] < elem[c]) {//交换swap(p,c);//将指向该结点的引用指向该结点的子结点,再重新将子结点的下标进行变化,检查该结点的子树是否满足大堆,不满足则继续向下调整p = c;c = 2*p + 1;} else {break;}}}//交换方法public void swap(int x, int y) {int tmp = elem[x];elem[x] = elem[y];elem[y] = tmp;}
2.4 堆的插入与删除
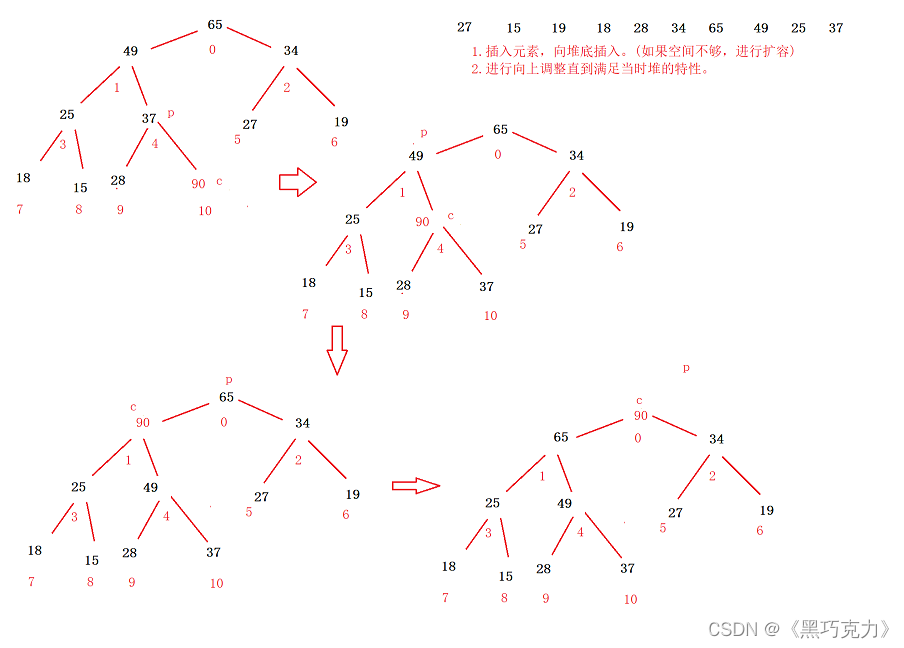
2.4.1 堆的插入
堆的插入总共需要两个步骤:
- 先将元素放入到底层空间中(注意:空间不够时需要扩容)
- 将最后新插入的节点向上调整,直到满足堆的性质
画图演示过程:
代码实现:
//堆的插入public void offer(int val) {//1.判断是否扩容if(isFull()) {this.elem = Arrays.copyOf(elem,2*elem.length);}//插入元素elem[usedSize] = val;usedSize++;//11//向上调整siftUp(usedSize-1);}private void siftUp(int child) {int parent = (child-1)>>>1; //>>>1等于除于2while(child > 0) {//判断child与parent的大小if(child >parent) {//交换swap(parent,child);//移动c与p的位置child = parent;parent = (child-1)>>>1;} else {break;}}}private boolean isFull() {return usedSize == elem.length;}
2.4.2 堆的删除
注意:堆的删除一定删除的是堆顶元素。具体如下:
- 将堆顶元素对堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整
代码实现:
//堆的删除(堆的删除一定是堆顶元素)public int poll() {//记录删除的元素int tmp = elem[0];//交换堆顶元素与最后一个元素swap(0,usedSize-1);//数组长度减1usedSize--;//对堆顶元素向下调整,因为这个堆本身之前是一个大堆,堆顶之下的结点基本都满足大堆的规则,所以只需要从堆顶的元素向下调整即可// 直到这个堆完全满足大堆的特性siftDown1(0,usedSize);return tmp;}//向下调整的方法public void siftDown1(int p,int end) {//得到该结点的子结点的下标int c = 2*p + 1;//临界条件:子结点的下标<数组的长度while(c < end) {//找到最大的子结点if(c+1<end && elem[c] < elem[c+1]) {c++;}//将该结点与最大子结点比较,如小于则交换否则直接break返回if(elem[p] < elem[c]) {//交换swap(p,c);//将指向该结点的引用指向该结点的子结点,再重新将子结点的下标进行变化,检查该结点的子树是否满足大堆,不满足则继续向下调整p = c;c = 2*p + 1;} else {break;}}}
3.常用接口介绍
3.1 PriorityQueue的特性
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,本文主要介绍PriorityQueue。
关于PriorityQueue的使用要注意:
- 使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue;
- PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出
ClassCastException异常 - 不能插入null对象,否则会抛出NullPointerException
- 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
- 插入和删除元素的时间复杂度为
- PriorityQueue底层使用了堆数据结构
- PriorityQueue默认情况下是小堆—即每次获取到的元素都是最小的元素
3.2 PriorityQueue常用接口介绍
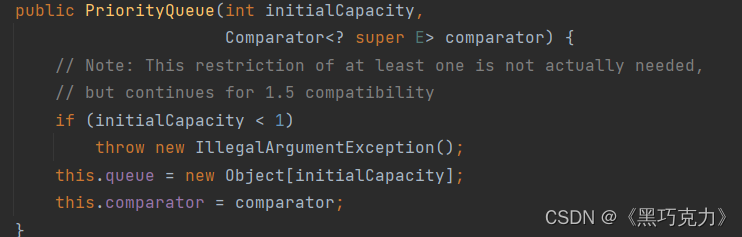
1. 优先级队列的构造
有四种PriorityQueue构造方式,分别为:
1.传空参数:

2:传数组的大小的参数:
3.传比较器参数:

4.数组大小和比较器都传:
注意:其实细心就会发现前三种不管传了什么,都会调用第四种方式。
这里我需要解释一下:
DEFAULT_INITIAL_CAPACITY:基本容量
Comparator<? super E> comparator: 比较器
这是PriorityQueue队列在创建堆的分析图:
默认情况下,PriorityQueue队列是小堆,如果需要大堆需要用户提供比较器
这是传了比较器,通过去重写compare方法,去创建大堆。

代码实现:
class Imp implements Comparator<Integer> {//通过自己建一个比较器来将小堆转化为大堆@Overridepublic int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}
public class PrioQueue {public static void main(String[] args) {PriorityQueue<Integer> priorityQueue1 = new PriorityQueue<>();priorityQueue1.offer(1);priorityQueue1.offer(2);System.out.println("======");Imp imp = new Imp();PriorityQueue<Integer> priorityQueue2= new PriorityQueue<>(imp);/*priorityQueue2.offer(1);priorityQueue2.offer(2);System.out.println("=========");*/
2.PriorityQueue队列的一些方法:

4.堆的应用
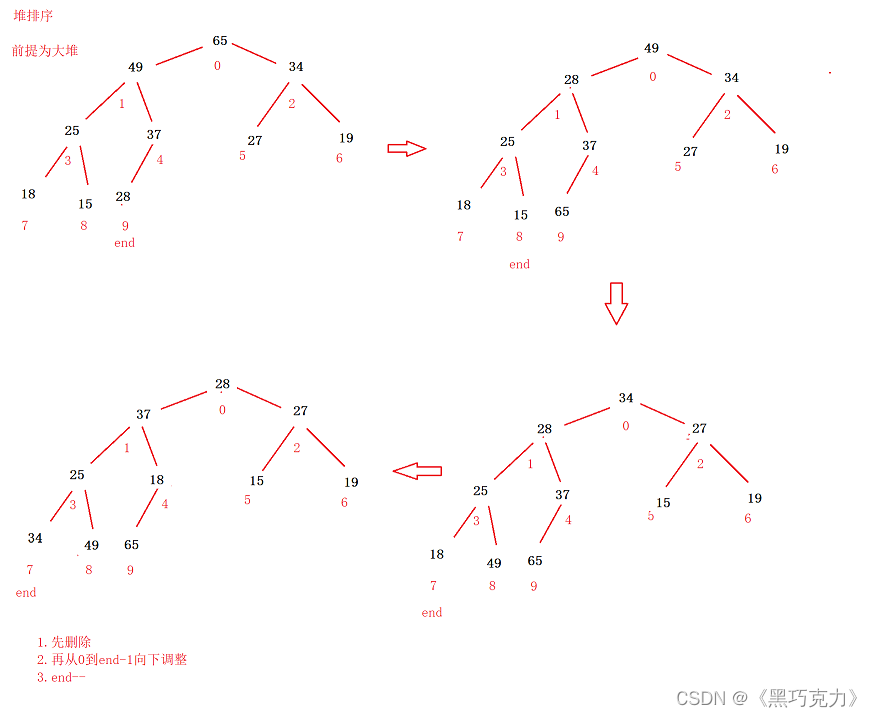
4.1堆排序
如果你需要将数据以升序的方式排序,则你必须要一个大根堆。
1.创建大根堆(前面实现了)
2.删除堆顶的元素
3.再从0到end-1向下调整
4.end–
画图演示:
代码实现:
public void heapSort() {int end = usedSize-1;while(end>0) {swap(0,end);siftDown1(0,end-1);end--;}}//向下调整的方法public void siftDown1(int p,int end) {//得到该结点的子结点的下标int c = 2*p + 1;//临界条件:子结点的下标<数组的长度while(c < end) {//找到最大的子结点if(c+1<end && elem[c] < elem[c+1]) {c++;}//将该结点与最大子结点比较,如小于则交换否则直接break返回if(elem[p] < elem[c]) {//交换swap(p,c);//将指向该结点的引用指向该结点的子结点,再重新将子结点的下标进行变化,检查该结点的子树是否满足大堆,不满足则继续向下调整p = c;c = 2*p + 1;} else {break;}}}//交换方法public void swap(int x, int y) {int tmp = elem[x];elem[x] = elem[y];elem[y] = tmp;}
4.2Top-k问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
代码实现:
public int[] smallestK(int[] arr, int k) {int[] tmp = new int[k];if (k == 0) {return tmp;}Imp imp = new Imp();PriorityQueue<Integer> maxHeap = new PriorityQueue<>(imp);// 建立大堆含k个元素for (int i = 0; i < k; i++) {maxHeap.offer(arr[i]);}// 从第k个元素遍历for (int j = k; j < arr.length; j++) {// 堆顶元素小于数组下标j的大小if (arr[j] < maxHeap.peek()) {maxHeap.poll();maxHeap.offer(arr[j]);}}// 打印这个大堆中的元素for (int i = 0; i < tmp.length; i++) {tmp[i] = maxHeap.poll();}return tmp;}*/
在求找出最小的数或者找出最大的数我们应该怎么做呢?
有知道的可以在评论区分享你的思路或者代码也行,下篇文章我们来解答这个问题。
希望大家可以从我的文章中学到东西,希望大家可以留下点赞收藏加关注🎉🎉🎉🎉🎉
相关文章:

【数据结构】优先级队列——堆
🧧🧧🧧🧧🧧个人主页🎈🎈🎈🎈🎈 🧧🧧🧧🧧🧧数据结构专栏🎈🎈🎈&…...

【力扣】45.跳跃游戏Ⅱ
45.跳跃游戏Ⅱ 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i]i j < n 返回到达 n…...

containerd使用了解
containerd使用了解 yum安装 [rootvm ~]# curl -o /etc/yum.repos.d/docker.repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo [rootvm ~]# yum list | grep containerd containerd.io.x86_64 1.6.28-3.1.el7 doc…...

gateway 分发时若两个服务的路由地址一样,怎么指定访问想要的服务下的地址
1.思路 在使用Spring Cloud Gateway时,如果两个服务的路由地址相同,可以通过Predicate(断言)和Filter(过滤器)的组合来实现根据请求的不同条件将请求分发到不同的服务下的地址。 使用Predicate进行路由条件…...

【LeetCode】三月题解
文章目录 [2369. 检查数组是否存在有效划分](https://leetcode.cn/problems/check-if-there-is-a-valid-partition-for-the-array/)思路:代码: [1976. 到达目的地的方案数](https://leetcode.cn/problems/number-of-ways-to-arrive-at-destination/) 思路…...

云手机:实现便携与安全的双赢
随着5G时代的到来,云手机在各大游戏、直播和新媒体营销中扮演越来越重要的角色。它不仅节约了成本,提高了效率,而且在边缘计算和云技术逐渐成熟的背景下,展现出了更大的发展机遇。 云手机的便携性如何? 云手机的便携性…...
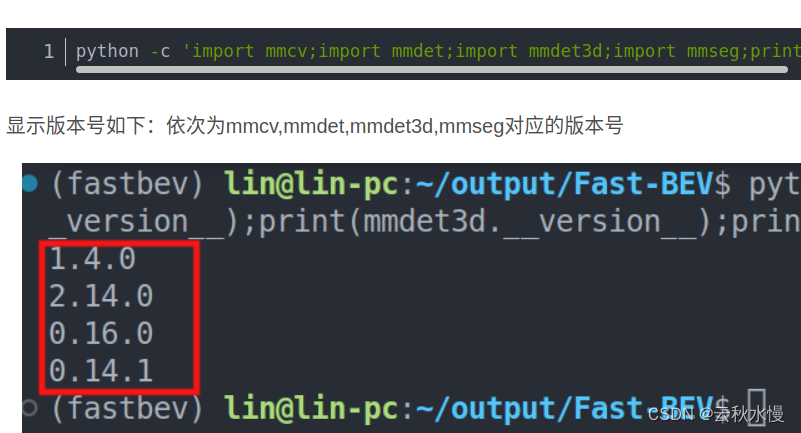
fast_bev学习笔记
目录 一. 简述二. 输入输出三. github资源四. 复现推理过程4.1 cuda tensorrt 版 一. 简述 原文:Fast-BEV: A Fast and Strong Bird’s-Eye View Perception Baseline FAST BEV是一种高性能、快速推理和部署友好的解决方案,专为自动驾驶车载芯片设计。该框架主要包…...
Collection与数据结构链表与LinkedList(三):链表精选OJ例题(下)
1. 分割链表 OJ链接 class Solution {public ListNode partition(ListNode head, int x) {if(head null){return null;//空链表的情况}ListNode cur head;ListNode formerhead null;ListNode formerend null;ListNode latterhead null;ListNode latterend null;//定义…...
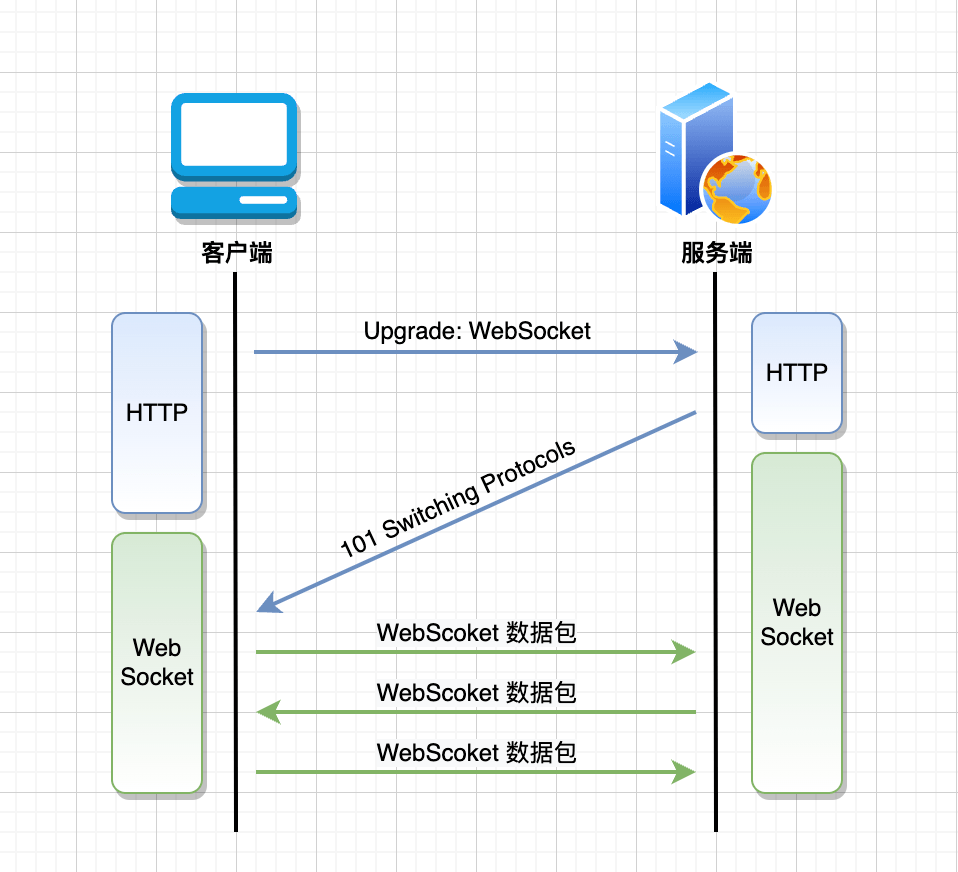
05 | Swoole 源码分析之 WebSocket 模块
首发原文链接:Swoole 源码分析之 WebSocket 模块 大家好,我是码农先森。 引言 WebSocket 是一种在单个 TCP 连接上进行全双工通信的协议。它允许客户端和服务器之间进行实时数据传输。 与传统的 HTTP 请求-响应模型不同,WebSocket 可以保持…...

Vue--------父子/兄弟组件传值
父子组件 子组件通过 props 属性来接受父组件的数据,然后父组件在子组件上注册监听事件,子组件通过 emit 触发事件来向父组件发送数据。 defineProps接收 let props defineProps({data: Array, }); defineModel接收 let bb defineModel("sit…...

Qt实现Kermit协议(一)
1 概述 Kermit文件运输协议提供了一条从大型计算机下载文件到微机的途径。它已被用于进行公用数据传输。 其特性如下: Kermit文件运输协议是一个半双工的通信协议。它支持7位ASCII字符。数据以可多达96字节长度的可变长度的分组形式传输。对每个被传送分组需要一个确认。Kerm…...
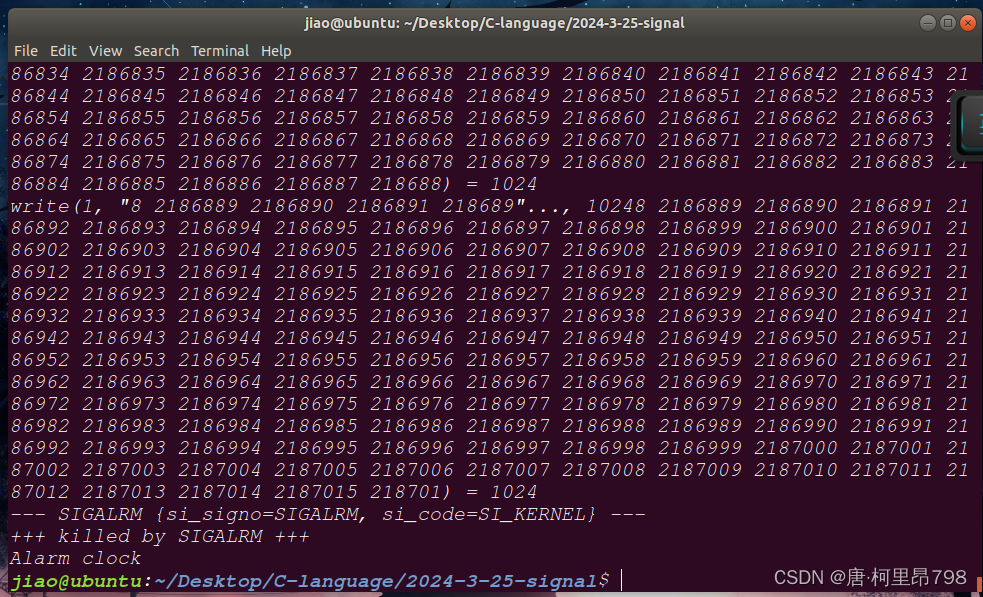
linux在使用重定向写入文件时(使用标准C库函数时)使处理信号异常(延时)--问题分析
linux在使用重定向写入文件时(使用标准C库函数时)使处理信号异常(延时)–问题分析 在使用alarm函数进行序号处理测试的时候发现如果把输出重定向到文件里面会导致信号的处理出现严重的延迟(ubuntu18) #include <stdio.h> #include <stdlib.h> #include <unist…...
淘宝扭蛋机小程序:趣味购物新体验,惊喜连连等你来
在数字化时代,淘宝始终站在创新的前沿,不断探索和引领电商行业的发展趋势。今天,我们欣然宣布,经过精心研发和打磨,淘宝扭蛋机小程序正式上线,为用户带来一场充满趣味与惊喜的购物新体验。 淘宝扭蛋机小程…...

linux:生产者消费者模型
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《Linux》 文章目录 前言一、生产者消费者模型二、基于阻塞队列的生产者消费者模型代码实现 总结 前言 本文是对于生产者消费者模型的知识总结 一、生产者消费者模型 生产者消费者模型就是…...

C++教学——从入门到精通 5.单精度实数float
众所周知,三角形的面积公式是(底*高)/2 那就来做个三角形面积计算器吧 到吗如下 #include"bits/stdc.h" using namespace std; int main(){int a,b;cin>>a>>b;cout<<(a*b)/2; } 这不对呀,明明是7.5而他却是7,…...

面向对象设计之单一职责原则
设计模式专栏:http://t.csdnimg.cn/6sBRl 目录 1.单一职责原则的定义和解读 2.如何判断类的职责是否单一 3.类的职责是否越细化越好 4.总结 1.单一职责原则的定义和解读 单一职责原则(Single Responsibility Principle,SRP)的描述:一个类…...

蓝桥杯真题:单词分析
import java.util.Scanner; //1:无需package //2: 类名必须Main, 不可修改 public class Main{public static void main(String[]args) {Scanner sannernew Scanner(System.in);String strsanner.nextLine();int []anew int [26];for(int i0;i<str.length();i) {a[str.charA…...

Python字符串字母大小写变换,高级Python开发技术
寻找有志同道合的小伙伴,互帮互助,群里还有不错的视频学习教程和PDF电子书! ‘’’ demo ‘tHis iS a GOod boOK.’ print(demo.casefold()) print(demo.lower()) print(demo.upper()) print(demo.capitalize()) print(demo.title()) print(dem…...

CentOS常用功能命令集合
1、删除指定目录下所有的空目录 find /xxx -type d -empty -exec rmdir {} 2、删除指定目录下近7天之前的日志文件 find /xxx -name "*.log" -type f -mtime 7 -exec rm -f {} \; 3、查询指定目录下所有的指定格式文件(比如PDF文件) find…...

黑马点评项目笔记 II
基于Stream的消息队列 stream是一种数据类型,可以实现一个功能非常完善的消息队列 key:队列名称 nomkstream:如果队列不存在是否自动创建,默认创建 maxlen/minid:设置消息队列的最大消息数量 *|ID 唯一id:…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
