机器学习实战17-高斯朴素贝叶斯(GaussianNB)模型的实际应用,结合生活中的生动例子帮助大家理解
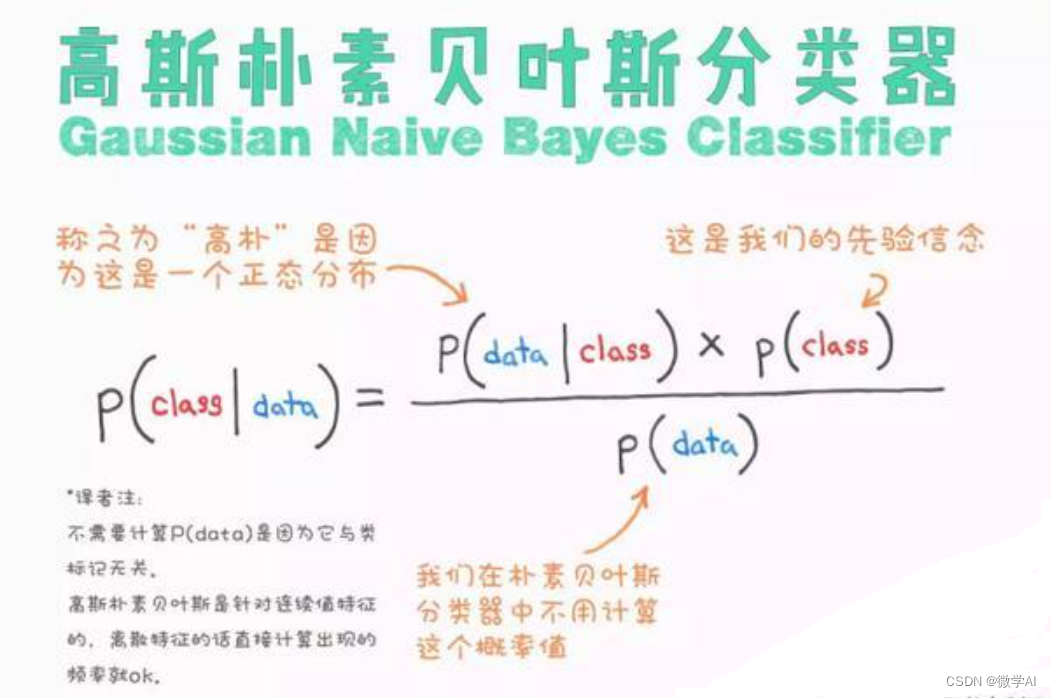
大家好,我是微学AI,今天给大家介绍一下机器学习实战17-高斯朴素贝叶斯(GaussianNB)模型的实际应用,结合生活中的生动例子帮助大家理解。GaussianNB,即高斯朴素贝叶斯模型,是一种基于概率论的分类算法,广泛应用于机器学习领域。该模型假设特征之间相互独立,并且每个特征服从高斯分布(正态分布),通过学习训练数据集中的先验概率和条件概率来实现对未知数据的预测。
在模型结构上,GaussianNB主要由两部分构成:一是各类别的先验概率,通过统计训练集中各类样本的数量得到;二是给定类别条件下各特征的概率分布参数,包括均值和方差,用于描述特征符合高斯分布的情况。在实际应用中,由于其算法简单、易于理解和实现,且对于大规模数据集有较高的处理效率,GaussianNB常被用于文本分类、情感分析、疾病诊断等多个场景。然而,该模型对输入数据的独立性假设较为严格,对于非线性或者相关性强的数据拟合效果可能不佳。
文章目录
- 一、GaussianNB模型概述
- 高斯朴素贝叶斯模型基本原理
- 应用场景举例
- 二、GaussianNB模型结构特点
- 参数估计
- 分类决策过程
- 三、GaussianNB模型实际应用案例
- 新闻分类任务
- 信用评分系统
- 四、GaussianNB模型的数学原理
- 五、GaussianNB模型的代码实现
- 六、总结
一、GaussianNB模型概述
高斯朴素贝叶斯模型基本原理
GaussianNB模型,即高斯朴素贝叶斯分类器,是一种基于概率论的分类方法,其核心思想是假设特征之间相互独立,并且每个特征都服从高斯分布(正态分布)。在训练阶段,该模型会为每个类别学习一个类条件概率分布,包括每个特征均值和方差。在预测阶段,它通过计算待测样本属于各个类别的概率并选择最高概率的类别作为预测结果。
具体来说,对于给定的数据集,GaussianNB首先计算每个特征在各类别下的均值和方差,然后利用贝叶斯公式计算待分类样本属于各个类别的后验概率,即P(类别|特征),并通过比较这些概率大小来决定样本的类别归属。
假设我们正在建立一个系统用于预测明天是否会下雨。我们收集了过去几天的三个特征数据:早晨的平均温度、湿度和云层厚度。我们可以使用GaussianNB模型,假设这三个特征彼此独立,并且各自在“下雨”和“不下雨”两种情况下的分布都是高斯分布。模型会分别计算出“下雨”和“不下雨”时这三个特征的平均值和方差。当需要预测明天是否下雨时,我们就将明天早晨的温度、湿度和云层厚度输入模型,模型会根据这些特征值计算出明天“下雨”和“不下雨”的概率,如果“下雨”的概率更高,则预测明天可能会下雨。这就是高斯朴素贝叶斯模型在实际生活中的应用。
应用场景举例
GaussianNB模型,全称为高斯朴素贝叶斯分类器,是一种基于概率论的分类算法,其核心思想是假设特征之间相互独立,并且每个特征服从高斯分布(正态分布)。在训练阶段,它会计算每个类别下各个特征的均值和方差,然后在预测阶段,利用贝叶斯定理计算待测样本属于各个类别的概率,并将其分到概率最高的类别中。
应用场景举例:
- 文本分类:如垃圾邮件识别,通过分析邮件中的关键词出现频率等特征,利用GaussianNB模型预测邮件是否为垃圾邮件。
- 医疗诊断:通过对病人的各种生理指标数据进行分析,如体温、血压、心率等,利用GaussianNB模型预测患者可能患有的疾病类型。
- 信用评分:在金融领域,通过分析用户的收入、年龄、职业、贷款历史等信息,使用GaussianNB模型预测用户违约的可能性。
假设你是一位水果摊主,需要快速判断顾客手中的水果是苹果还是橙子,但只能观察重量和颜色这两个特征。经过长期观察,你知道苹果和橙子的重量分别服从某个平均值和标准差的正态分布,颜色也有特定的概率分布。这时,GaussianNB模型就像你的智能助手,当你给它提供一个水果的重量和颜色时,它就会根据之前学习到的分布规律,计算这个水果更可能是苹果还是橙子,从而帮助你快速分类。例如,如果水果重量较轻且颜色偏红,那么模型可能会告诉你这更有可能是苹果。
二、GaussianNB模型结构特点
参数估计
GaussianNB,即高斯朴素贝叶斯分类器,是一种基于概率论的分类算法,其核心思想是假设特征之间相互独立,并且每个特征都服从高斯分布(正态分布)。在模型结构上,对于每一个类别,GaussianNB都会为每个特征估计一个均值和方差,形成该类别的高斯分布参数。
在参数估计阶段,GaussianNB会计算每个类别下各个特征的均值和方差。均值代表了该特征在该类别下的典型取值,而方差则反映了数据点围绕均值分散的程度。训练过程中,模型通过遍历所有样本,对各类别下的各特征分别进行统计分析,从而得到这些参数。
假设我们正在建立一个模型来预测明天是否会下雨。我们的特征包括早晨的平均温度(Temp)、湿度(Humidity)和风速(WindSpeed)。GaussianNB模型会分别计算出晴天和雨天时这三个特征各自的均值和方差。例如,如果历史数据显示雨天时早晨的平均温度通常较低,湿度较高,风速适中,那么模型就会为“雨天”这一类别下的“温度”、“湿度”和“风速”特征估计出对应的均值和方差。当新的观测数据到来时,模型将利用这些预估的高斯分布参数,计算出明天是晴天还是雨天的概率,并以此作为预测结果。
分类决策过程
GaussianNB模型,即高斯朴素贝叶斯分类器,是一种基于概率论的分类方法。其主要特点是假设特征之间相互独立,并且每个特征都服从高斯分布(正态分布)。在决策过程中,它首先计算各个类别的先验概率,然后对每一个特征,分别计算该特征在各类别下的条件概率。对于待分类样本,通过将各个特征的条件概率相乘得到该样本属于各类别的后验概率,最后将其归到后验概率最高的类别中。
假设我们正在帮助一家水果店根据水果的颜色、大小和重量来区分苹果和橙子。GaussianNB模型就像一个聪明的助手,它首先观察大量已知种类的水果,统计出苹果和橙子各自出现的比例(先验概率)。然后,它发现苹果的颜色、大小和重量各自都有一个大致的正态分布范围。当有新的未知水果到来时,助手会分别测量其颜色、大小和重量,看这三个特征分别更接近苹果还是橙子的概率分布,然后将这三个概率相乘得到该水果是苹果或橙子的总概率(后验概率),并最终判断它是苹果还是橙子。这就是GaussianNB模型的决策过程。
三、GaussianNB模型实际应用案例
新闻分类任务
在新闻分类任务中,GaussianNB(高斯朴素贝叶斯)模型是一种常用的机器学习算法。该模型基于朴素贝叶斯理论,假设特征之间相互独立,并且每个特征服从高斯分布(正态分布)。具体应用时,首先对训练集中的新闻数据进行预处理,包括文本清洗、分词、提取关键词等步骤,将文本信息转化为数值型特征向量。然后利用GaussianNB模型对这些特征向量进行学习,得到各类新闻的特征分布参数。
例如,在一个在线新闻平台中,我们想要自动分类新闻为体育、科技或娱乐类别。每篇新闻都可以看作是一个“包裹”,其中包含多个“物品”(如关键词、作者、发布时间等特征)。GaussianNB模型就像一位快递员,他通过学习过往“包裹”的内容和对应标签,了解了各类新闻的特征规律。比如,如果“篮球”、“足球”等关键词常出现在体育类新闻中,而“AI”、“5G”等词更常见于科技类新闻,那么当收到新的“包裹”时,模型就能根据其中“物品”的组合情况,快速判断这篇新闻最可能属于哪个类别,从而实现自动化分类。
信用评分系统
在信用评分系统中,GaussianNB(高斯朴素贝叶斯)模型是一种广泛应用的机器学习算法。该模型基于朴素贝叶斯理论,假设特征之间相互独立,并且每个特征都服从高斯分布(正态分布)。在信用评估场景下,我们可能拥有一系列用户数据,如年龄、收入、贷款历史、信用卡欠款额度等。
例如,某银行正在构建一个自动化的信用评分系统以决定是否给申请人发放贷款以及确定贷款额度。通过收集大量用户的信用数据,并利用GaussianNB模型进行训练,模型会学习到各个特征与信用好坏之间的关系及其概率分布。
具体来说,模型会计算“年龄为30岁、年收入10万、无贷款历史、信用卡欠款5000元”的用户违约的概率是多少。在预测阶段,新申请人的信息输入模型后,模型将依据学习到的概率分布和其他申请人违约的历史情况,给出该申请人信用风险的评分。
假设你是一位水果摊主,你在过去的经验中发现,购买苹果的人群中,年轻人更倾向于选择红苹果,而年纪稍大的人更喜欢青苹果。此外,收入较高的人群购买大苹果的可能性更大。于是,当你面对一位新的顾客时,你会根据他的年龄和外表判断其可能的购买喜好(红苹果或青苹果),这就是朴素贝叶斯分类器在现实生活中的应用。而在信用评分系统中,GaussianNB模型就是那位“水果摊主”,它通过学习各种特征与信用表现的关系,来预测新申请人的信用风险。
四、GaussianNB模型的数学原理
在机器学习中,Gaussian Naive Bayes (GaussianNB) 模型是一种基于贝叶斯定理和高斯分布的概率分类器。其核心思想是假设特征之间相互独立,并且每个特征都服从高斯分布(正态分布)。以下是GaussianNB模型的数学原理:
对于给定的数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } D = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\} D={(x1,y1),(x2,y2),...,(xN,yN)},其中 x i ∈ R d x_i \in \mathbb{R}^d xi∈Rd 是一个d维特征向量, y i ∈ { C 1 , C 2 , . . . , C k } y_i \in \{C_1, C_2, ..., C_k\} yi∈{C1,C2,...,Ck} 是对应的类别标签。
对于每一个类别 C j C_j Cj,GaussianNB模型假设每个特征 x i j x_{ij} xij 都独立地服从高斯分布:
p ( x i j ∣ y = C j ) = 1 2 π σ j 2 exp ( − ( x i j − μ j ) 2 2 σ j 2 ) p(x_{ij}|y=C_j) = \frac{1}{\sqrt{2\pi\sigma_{j}^2}} \exp\left(-\frac{(x_{ij} - \mu_{j})^2}{2\sigma_{j}^2}\right) p(xij∣y=Cj)=2πσj21exp(−2σj2(xij−μj)2)
其中, μ j \mu_j μj 是类别 C j C_j Cj 对应的第i个特征的均值, σ j 2 \sigma_j^2 σj2 是类别 C j C_j Cj 对应的第i个特征的方差。
在预测阶段,利用贝叶斯定理计算后验概率:
P ( y = C j ∣ x ) = P ( y = C j ) ∏ i = 1 d P ( x i ∣ y = C j ) ∑ l = 1 k P ( y = C l ) ∏ i = 1 d P ( x i ∣ y = C l ) P(y=C_j|x) = \frac{P(y=C_j) \prod_{i=1}^{d} P(x_i|y=C_j)}{\sum_{l=1}^{k} P(y=C_l) \prod_{i=1}^{d} P(x_i|y=C_l)} P(y=Cj∣x)=∑l=1kP(y=Cl)∏i=1dP(xi∣y=Cl)P(y=Cj)∏i=1dP(xi∣y=Cj)
其中, P ( y = C j ) P(y=C_j) P(y=Cj) 是先验概率,可以通过训练数据集中各类别的频率估计得到。 模型将预测使得后验概率最大的类别作为新的观测样本的类别。
五、GaussianNB模型的代码实现
在PyTorch中,Gaussian Naive Bayes (GaussianNB) 模型并不是一个内置模型,因为PyTorch主要关注神经网络和深度学习。然而,你可以基于sklearn的GaussianNB实现自行构建一个简单的版本。以下是一个使用numpy和sklearn GaussianNB的示例,然后我们将数据转换为PyTorch tensors进行处理:
import numpy as np
from sklearn.naive_bayes import GaussianNB
import torch# 假设我们有如下数据
X_train = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y_train = np.array([0, 0, 1, 1])# 使用sklearn的GaussianNB训练模型
gnb = GaussianNB()
gnb.fit(X_train, y_train)# 定义一个函数将预测过程封装起来,以便于处理PyTorch Tensors
def predict_gnb(x):x = x.numpy() # 将Tensor转化为numpy数组return gnb.predict(x)# 创建一个PyTorch Tensor作为测试数据
X_test_torch = torch.tensor([[9, 10], [11, 12]])# 使用封装好的predict函数进行预测
predictions = predict_gnb(X_test_torch)
print(predictions)
请注意,上述代码并没有直接在PyTorch中实现GaussianNB,而是利用了sklearn的实现,并通过适配使得其能处理PyTorch的Tensors。如果你想在纯PyTorch环境中实现GaussianNB,你需要自己编写相关的概率密度估计、似然计算以及分类逻辑等代码,这通常比直接使用sklearn要复杂得多。
六、总结
GaussianNB,即高斯朴素贝叶斯模型,是一种基于概率论的高效分类算法,在机器学习领域应用广泛。该模型的核心在于其对特征独立性和高斯分布的假设,通过计算训练集中各类别的先验概率以及在给定类别下各特征的高斯分布参数(如均值和方差),从而实现对未知数据的预测。尽管模型结构简洁,但其在处理大规模数据集时表现出高效能,尤其适用于文本分类、情感分析及疾病诊断等场景。然而,由于其对输入数据独立性的严格要求,当面对非线性或强相关性数据时,GaussianNB模型的拟合效果可能会受限。尽管如此,因其算法理解与实现相对简单,GaussianNB仍不失为一种实用且有价值的机器学习工具。
相关文章:

机器学习实战17-高斯朴素贝叶斯(GaussianNB)模型的实际应用,结合生活中的生动例子帮助大家理解
大家好,我是微学AI,今天给大家介绍一下机器学习实战17-高斯朴素贝叶斯(GaussianNB)模型的实际应用,结合生活中的生动例子帮助大家理解。GaussianNB,即高斯朴素贝叶斯模型,是一种基于概率论的分类算法,广泛应…...

数据处理库Pandas数据结构DataFrame
Dataframe是一种二维数据结构,数据以表格形式(与Excel类似)存储,有对应的行和列,如图3-3所示。它的每列可以是不同的值类型(不像 ndarray 只能有一个 dtype)。基本上可以把 DataFrame 看成是共享…...

中国发展新能源的核心驱动力是什么?其原理是如何运作的?
中国发展新能源的核心驱动力是推进能源消费方式变革、构建多元清洁能源供应体系、实施创新驱动发展战略、深化能源体制改革和持续推进国际合作。 新能源的发展背后有多重经济、政策及环境因素的推动: 经济发展需求:随着中国经济的快速发展,…...
skywalking
部署: docker部署方式 docker-compose.yaml version: 3 services:elasticsearch:build:context: elasticsearchrestart: alwaysnetworks:- skywalking_netcontainer_name: elasticsearchimage: elasticsearch:7.17.6environment:- "discovery.typesingle-no…...
 060108》第二次过程性考核作业参考答案)
江苏开放大学2024年春《大学英语(D) 060108》第二次过程性考核作业参考答案
答案:更多答案,请关注【电大搜题】微信公众号 答案:更多答案,请关注【电大搜题】微信公众号 答案:更多答案,请关注【电大搜题】微信公众号 单选题 1从选项中选出翻译最为准确的一项。 We cannot help …...

dockerfile制作-pytoch+深度学习环境版
你好你好! 以下内容仅为当前认识,可能有不足之处,欢迎讨论! 文章目录 文档内容docker相关术语docker常用命令容器常用命令根据dockerfile创建容器dokerfile文件内容 docker问题:可能的原因和解决方法示例修改修改后的D…...

YOLOv8结合SCI低光照图像增强算法!让夜晚目标无处遁形!【含端到端推理脚本】
这里的"SCI"代表的并不是论文等级,而是论文采用的方法 — “自校准光照学习” ~ 左侧为SCI模型增强后图片的检测效果,右侧为原始v8n检测效果 这篇文章的主要内容是通过使用SCI模型和YOLOv8进行算法联调,最终实现了如上所示的效果:在增强图像可见度的同时,对图像…...
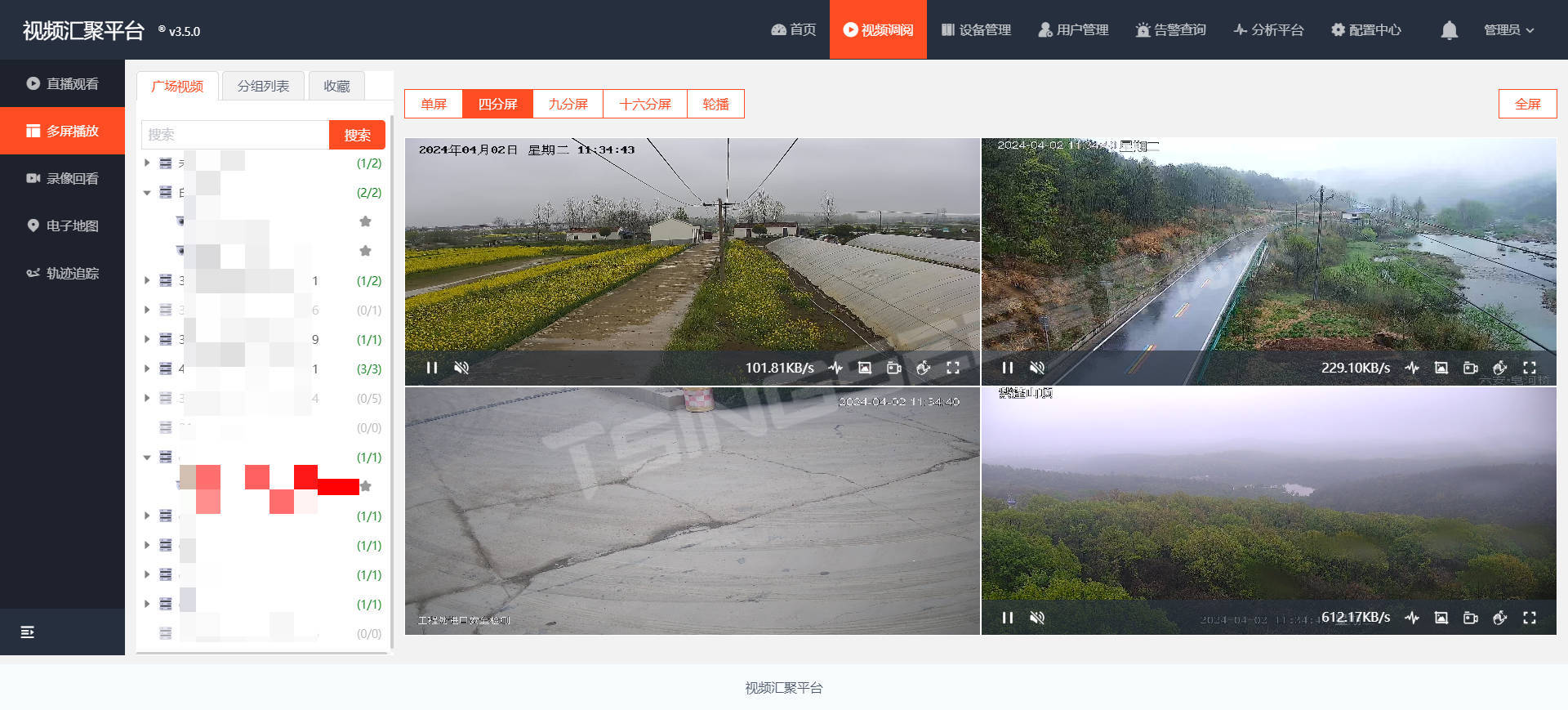
视频监控/云存储/AI智能分析平台EasyCVR集成时调用接口报跨域错误的原因
EasyCVR视频融合平台基于云边端架构,可支持海量视频汇聚管理,能提供视频监控直播、云端录像、云存储、录像检索与回看、智能告警、平台级联、智能分析等视频服务。平台兼容性强,支持多协议、多类型设备接入,包括:国标G…...

VuePress基于 Vite 和 Vue 构建优秀框架
VitePress 是一个静态站点生成器 (SSG),专为构建快速、以内容为中心的站点而设计。简而言之,VitePress 获取用 Markdown 编写的内容,对其应用主题,并生成可以轻松部署到任何地方的静态 HTML 页面。 VitePress 附带一个用于技术文档…...
)
冒泡排序,选择排序,插入排序,希尔排序,基数排序,堆排序代码分析(归并排序和快速排序后续更新)
所有的算法都是这样,算法思想最重要,其次是实现过程,最后才是实现的代码 上战伐谋,我们只要明确了其算法思想和实现过程,所有算法都是纸老虎,所有算法题都是纸老虎 笔者才疏学浅,也算是刚刚接…...

从入门到精通:NTP卫星时钟服务器技术指南
从入门到精通:NTP卫星时钟服务器技术指南 从入门到精通:NTP卫星时钟服务器技术指南 一、 产品功能 卫星时钟服务器是一款采用GPS或北斗卫星提供高精度网络时间服务的产品。卫星天线安装简便(根据天线所放位置提示实时卫星颗数)&a…...

OpenResty基于来源IP和QPS来限流
Nginx 经典限流法 ngx_http_limit_req_module 和 ngx_http_limit_conn_module,可以在代理层面对服务进行限流和熔断。 http {# 请求限流定义1:# - $binary_remote_addr:限制对象(客户端)# - zone:定义限制(策略)名称# - 10m:用十…...

面对AI技术创业的挑战以及提供给潜在创业者的一些建议
面对AI创业的挑战 AI技术创业虽然机遇众多,但也面临不少挑战,理解这些挑战并寻找应对策略是创业成功的关键。 技术挑战 AI技术的快速发展意味着创业者需要持续学习和更新知识库,以保持技术竞争力。同时,AI项目往往需要处理大量数…...

`require`与`import`的区别
require与import的区别主要体现在以下几个方面: 1.加载时间不同。require是在运行时加载模块,这意味着模块的加载和执行可以在代码的任何地方进行,也可以在运行时根据条件动态地加载不同的模块;import是在编译时加载模块…...

中介者模式:优雅解耦的利器
在软件设计中,随着系统功能的不断扩展,对象之间的依赖关系往往会变得错综复杂,导致系统难以维护和扩展。为了降低对象之间的耦合度,提高系统的可维护性和可扩展性,设计模式应运而生。中介者模式(Mediator P…...

Ubuntu20.04安装MatlabR2018a
一、安装包 安装包下载链接 提取码:kve2 网上相关教程很多,此处仅作为安装软件记录,方便后续软件重装,大家按需取用。 二、安装 1. 相关文件一览 下载并解压文件后,如下图所示: 2. 挂载镜像并安装 2…...
基于SpringBoot的图书馆管理系统设计与实现
介绍 基于:java8 SpringBoot thymeleaf MySQL8.0.17 mybatis-plus maven Xadmin 实现图书馆管理系统 系统要实现如下的基本管理功能: (1)用户分为两类:管理员,一般用户。 (2)…...

网易云首页单页面html+css
网页设计与网站建设作业htmlcss 预览 源码查看https://hpc.baicaitang.cn/2083.html...

acwing算法提高之图论--最小生成树的典型应用
目录 1 介绍2 训练 1 介绍 本专题用来记录使用prim算法或kruskal算法求解的题目。 2 训练 题目1:1140最短网络 C代码如下, #include <iostream> #include <cstring>using namespace std;const int N 110, INF 0x3f3f3f3f; int g[N][N…...
springcloud基本使用二(远程调用)
创建两个springboot maven子项目 子项目名称分别为order-server和user-server 配置user-server子项目: 所需依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId> </dependenc…...

Yi-Coder-1.5B实战:VSCode配置C/C++环境一键部署指南
Yi-Coder-1.5B实战:VSCode配置C/C环境一键部署指南 1. 引言 你是不是也遇到过这样的情况:刚装好VSCode准备写C代码,却发现编译运行都报错,配置环境变量、安装插件、设置路径...一堆麻烦事让人头疼。传统的C/C开发环境配置确实复…...

Beyond Compare 5本地授权与密钥配置完全指南
Beyond Compare 5本地授权与密钥配置完全指南 【免费下载链接】BCompare_Keygen Keygen for BCompare 5 项目地址: https://gitcode.com/gh_mirrors/bc/BCompare_Keygen 在软件开发与数据管理过程中,文件对比工具是不可或缺的效率工具。Beyond Compare作为行…...

CHORD-X创意写作模式展示:生成科幻背景下的“未来科技趋势研究报告”
CHORD-X创意写作模式展示:生成科幻背景下的“未来科技趋势研究报告” 最近在试用各种大模型时,我一直在想,除了写文案、做翻译这些常规操作,它们能不能干点更有想象力的事?比如,让AI基于一套逻辑ÿ…...

OFA-SNLI-VE模型效果展示:‘there are’与‘there is’语法敏感性
OFA-SNLI-VE模型效果展示:‘there are’与‘there is’语法敏感性 1. 模型效果惊艳展示 OFA-SNLI-VE模型在视觉蕴含任务中展现出了令人印象深刻的语言理解能力,特别是在英语语法细节的敏感性方面。这个基于阿里巴巴达摩院OFA架构的模型,不仅…...

Ubuntu22系统下ROS2的完整安装与彻底卸载指南
1. 为什么选择在Ubuntu 22.04上手动安装ROS2? 如果你正在踏入机器人开发的世界,或者正准备从ROS1迁移到ROS2,那么Ubuntu 22.04 LTS(Jammy Jellyfish)搭配ROS2 Humble Hawksbill绝对是一个黄金组合。我刚开始接触ROS2的…...
 安全性测试:防止“守门人”沦陷)
数据安全治理平台 (DSGP) 安全性测试:防止“守门人”沦陷
前言 技术背景:在现代网络攻防体系中,数据是攻防双方争夺的核心。数据安全治理平台 (DSGP),作为集中管理企业数据分类、权限、脱敏和审计的关键基础设施,是数据防线的指挥中心。传统攻击往往绕过它窃取数据,但更高级的…...

Maxwell Optislang的谐响应与多物理场计算在永磁电机多目标优化参数化建模及电磁振...
maxwell ,optislang 谐响应,,多物理场计算永磁电机多目标优化参数化建模电磁振动噪声仿真永磁电机的多物理场优化就像在玩一场精密的多维拼图游戏。当电磁性能、振动噪声和热特性这几个看似矛盾的指标需要同时满足时,传统单学科优…...

IonicSelect组件使用指南
ionic select 基础用法ionic select 组件允许用户从一组选项中选择一个或多个值。基本用法需要在 ion-select 标签内嵌套 ion-select-option 标签。<ion-select placeholder"选择水果"><ion-select-option value"apple">苹果</ion-select-o…...

Flutter 三方库 icc_parser 的鸿蒙化适配指南 - 高效解析 ICC 颜色配置文件,精准还原跨平台色彩表现
欢迎加入开源鸿蒙跨平台社区:https://openharmonycrossplatform.csdn.net Flutter 三方库 icc_parser 的鸿蒙化适配指南 - 高效解析 ICC 颜色配置文件,精准还原跨平台色彩表现 前言 在现代移动应用开发中,色彩的准确性对于提升 UI 质感和用…...

anime4kCPP在windows上部署记录
文章目录 前言 在windows编译 如何使用 结果 python脚本批量调用 前言 Anime4KCPP 是由开发者 TianZerL 基于著名的 Anime4K 算法,使用 C++ 重新实现并优化的高性能动漫超分辨率工具。 简单来说,它的核心任务是:把模糊、低分辨率的动漫图片或视频,变得清晰且高分辨率(例如…...
