DDD 的四层领域模型是怎样的?包含哪些基础概念?

DDD的四层领域模型如下所示:
- 展现层:这一层负责向用户显示信息和解释用户命令,完成前端界面逻辑。并将用户请求传递给应用层。
- 应用层:这一层是很薄的一层,负责协调领域层中的领域对象,组成具体应用场景。应用层要尽量简单,不包含业务规则或者知识,不保留业务对象的状态,只保留有应用任务的进度状态,更注重流程性的东西。应用层直接依赖于领域层,由领域层提供具体的业务能力。
- 领域层:这是业务软件的核心所在,包含了业务所涉及的领域对象(实体、值对象)、领域服务以及它们之间的关系,负责表达业务概念、业务状态信息以及业务规则,具体表现形式就是领域模型。DDD 强调领域层不需要任何外部依赖,只是反应软件核心的业务能力。
- 基础设施层:这一层向其他层提供通用的技术能力,为应用层传递消息(API 网关等),为领域层提供持久化机制(如数据库资源)等。
在四层领域模型中,展现层与应用层组成了前端应用,领域层与基础设施层组成了后端应用。前后端应用通过API进行通信。
在DDD中,还有一些基础概念需要了解。其中,聚合根是一个很重要的概念,它代表了一个业务对象群在领域模型中的根节点,可以包含其他多个实体和值对象。聚合根负责管理其包含的对象的状态,以保证其整体的一致性。另外,DDD还提倡使用限界上下文来构建子域,每个限界上下文代表了一个独立的业务能力或主题,可以包含特定的业务逻辑和数据。这些基础概念可以帮助开发人员更好地理解和构建领域模型。
相关文章:

DDD 的四层领域模型是怎样的?包含哪些基础概念?
DDD的四层领域模型如下所示: 展现层:这一层负责向用户显示信息和解释用户命令,完成前端界面逻辑。并将用户请求传递给应用层。应用层:这一层是很薄的一层,负责协调领域层中的领域对象,组成具体应用场景。应…...

AI 在医疗保健领域的应用:技术、趋势和前景
人工智能(AI)在医疗保健领域的应用已经成为引人瞩目的发展方向,其在医学影像分析、疾病诊断和个性化治疗等方面展现出了巨大潜力。本文将深入探讨这些技术应用和未来的发展趋势。 医学影像分析 医学影像分析是AI在医疗领域中应用最广泛的领…...

SVG XML 格式定义图形入门介绍
SVG SVG means Scalable Vector Graphics. SVG 使用 XML 格式定义图形SVG 图像在放大或改变尺寸的情况下其图形质量不会有所损失SVG 是万维网联盟的标准 Hello World Use SVG in html and you can see: Link to the SVG file You can use <a> tag to link to the svg…...

MYSQL数据库的故障排除与优化
目录 一.MySQL单实例故障排查 故障现象1 故障现象 2 故障现象 3 故障现象 4 故障现象 5 故障现象 6 故障现象 7 故障现象 8 二.主从环境常见故障 1.故障一 2. 故障二 3. 故障三 三. 优化 1.SQL优化 2. 架构优化 3.硬件方面 1.1 关于CPU 1.2 关于内存 1.3 关…...

C++从入门到精通——入门知识
1. C关键字(C98) C总计63个关键字,C语言32个关键字 2. 命名空间 在C/C中,变量、函数和后面要学到的类都是大量存在的,这些变量、函数和类的名称都将存在于全局作用域中,可能会导致很多冲突。使用命名空间的目的就是对标识符的名…...
一些题目学习
1.打开文件添加helloworld public class Saier {public static void main(String[] args){String path"C:\\Users\\sjg\\Desktop\\abc.txt";String text"hello world";try {File file new File(path);FileWriter fileWriter new FileWriter(file,true);…...
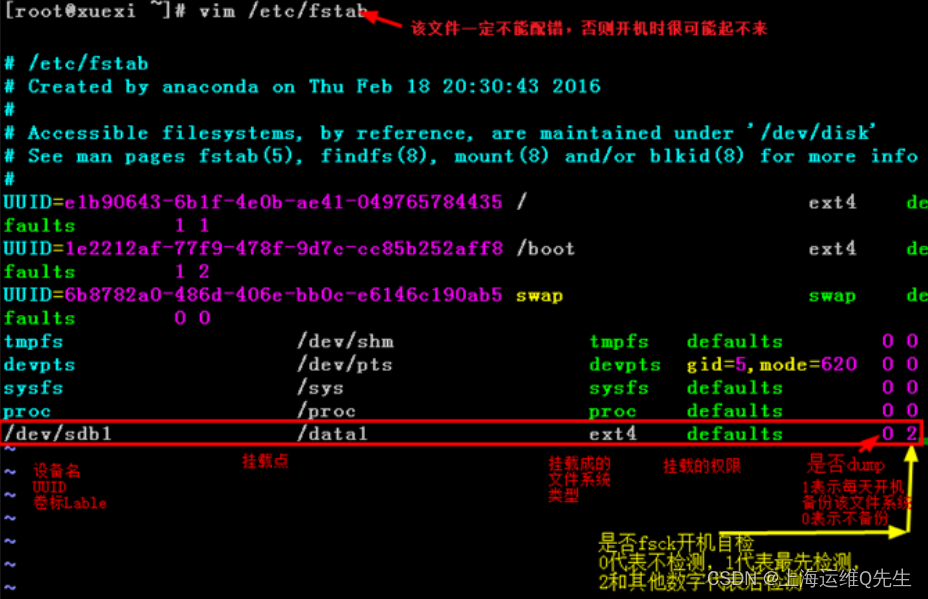
Linux上管理文件系统
Linux上管理文件系统 机械硬盘 机械硬盘由多块盘片组成,它们都绕着主轴旋转。每块盘片上下方都有读写磁头悬浮在盘片上下方,它们与盘片的距离极小。在每次读写数据时盘片旋转,读写磁头被磁臂控制着不断的移动来读取其中的数据。 所有的盘片…...

【Linux】寿司线程池{单例模式之懒汉模式下的线程池}
文章目录 回顾单例模式0.多线程下的单例模式的意义1.什么是单例模式1.0设计模式1.1C单例模式的介绍及原理1.2拷贝构造和赋值重载的处理1.3if (nullptr ptr),nullptr放在比较运算符的前面?1.4实现单例模式的方式 2.实现懒汉方式的单例模式2.1单线程的单例模式2.2多…...

Docker资源管理和分配指南
什么是cgroup? cgroups其名称源自控制组群(control groups)的简写,是Linux内核的一个功能,用来限制、控制与分离一个进程组(如CPU、内存、磁盘输入输出等)。 什么是Docker资源限制?…...

为什么索引的底层结构是B+树
B树 1.数据库与数据交互的单位是page,而B树的每个节点都是一个page,访问一个节点,就相当于进行了一次I/O操作。所以访问的节点越少,查找效率越大。而B树是矮胖的,查找深度也不会太大。 2.B树中的节点是有序存储的,对于范围查询、排…...

NLP学习路线指南总结
当然可以,以下是一份较为详细的NLP学习路线指南,帮助你逐步掌握自然语言处理的核心技术和应用。 一、基础知识与技能 语言学基础: 语言学基本概念:语音、语法、语义等。语言的层次与分类:语音学、音系学、句法学、语…...
试过了,ChatGPT确实不用注册就可以使用了!
看到官网说不用登录也可以直接使用ChatGPT 我们来试一下 直接打开官网 默认是直接进入了chatgpt3.5的聊天界面 之前是默认进的登录页面 聊一下试试 直接回复了,目前属于未登录状态,挺好! 来试下ChatGPT4 跳转到了登录页面 目前来看gpt4还…...

CANoe自带的TCP/IP协议栈中TCP的keep alive机制是如何工作的
TCP keep alive机制我们已经讲过太多次,车内很多控制器的TCP keep alive机制相信很多开发和测试的人也配置或者测试过。我们今天想知道CANoe软件自带的TCP/IP协议栈中TCP keep alive机制是如何工作的。 首先大家需要知道TCP keep alive的参数有哪些?其实就三个参数:CP_KEEP…...

【C++练级之路】【Lv.18】哈希表(哈希映射,光速查找的魔法)
快乐的流畅:个人主页 个人专栏:《算法神殿》《数据结构世界》《进击的C》 远方有一堆篝火,在为久候之人燃烧! 文章目录 引言一、哈希1.1 哈希概念1.2 哈希函数1.3 哈希冲突 二、闭散列2.1 数据类型2.2 成员变量2.3 默认成员函数2.…...

「PHP系列」If...Else语句/switch语句
文章目录 一、If...Else语句1. 基本语法2. 带有 elseif 的语法3. 示例示例 1:基本 if...else 结构示例 2:使用 elseif示例 3:嵌套 if...else 结构 4. 注意事项 二、switch语句1. 基本语法2. 示例示例 1:基本 switch 结构示例 2&am…...
Ubuntu部署BOA服务器
BOA服务器概述 BOA是一款非常小巧的Web服务器,源代码开放、性能优秀、支持CGI通用网关接口技术,特别适合用在嵌入式系统中。 BOA服务器主要功能是在互联嵌入式设备之间进行信息交互,达到通用网络对嵌入式设备进行监控,并将反馈信…...

安卓Glide加载失败时点击按钮重新加载图片
需求 假设此时已经用load指定一个url: String,又用into指定了一个img: ImageView开始加载,但是网络突然中断,导致图片加载失败。在这种情况下,想要通过点击一个Button重新加载。 Glide.with(context).load(url).placeholder(loa…...
启动)
linux下python服务定时(自)启动
AI应用开发相关目录 本专栏包括AI应用开发相关内容分享,包括不限于AI算法部署实施细节、AI应用后端分析服务相关概念及开发技巧、AI应用后端应用服务相关概念及开发技巧、AI应用前端实现路径及开发技巧 适用于具备一定算法及Python使用基础的人群 AI应用开发流程概…...
)
awk命令进阶操作(二)
awk模块 awk模块awk的BEGIN模块和END模块BEGIN模块BEGIN 常见错误END模块END模块 常见错误 案例计算1~100的累加和统计系统中有多少用户的shell类型是/bin/bash awk模块 awk的BEGIN模块和END模块 格式 awk BEGIN{}{}END{} 文件名BEGIN模块 用于定义一个动作,用{…...

【洛谷 P8695】[蓝桥杯 2019 国 AC] 轨道炮 题解(映射+模拟+暴力枚举+桶排序)
[蓝桥杯 2019 国 AC] 轨道炮 题目描述 小明在玩一款战争游戏。地图上一共有 N N N 个敌方单位,可以看作 2D 平面上的点。其中第 i i i 个单位在 0 0 0 时刻的位置是 ( X i , Y i ) (X_i, Y_i) (Xi,Yi),方向是 D i D_i Di (上下左右之一, 用…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
