力扣经典150题第二题:移除元素
移除元素问题详解与解决方法
1. 介绍
移除元素问题是 LeetCode 经典题目之一,要求原地修改输入数组,移除所有数值等于给定值的元素,并返回新数组的长度。
问题描述
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,3,0,4]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
2. 解题思路
方法一:双指针法
利用双指针技巧,一个指针 slow 在前,一个指针 fast 在后,当 fast 指向的元素等于给定值时,将 fast 指针后移;当 fast 指向的元素不等于给定值时,将 fast 指向的元素复制到 slow 指向的位置,并同时移动 slow 和 fast 指针。
方法二:快慢指针法
维护一个下标 index,初始值为 0,遍历数组,如果当前元素不等于给定值,则将其复制到 index 位置,并将 index 后移。
方法三:交换移除法
维护两个指针 left 和 right,分别指向数组的首尾,当 nums[left] 等于给定值时,将 nums[left] 和 nums[right] 交换,并将 right 指针左移;否则,将 left 指针右移。
3. 算法实现
方法一实现代码
public int removeElement(int[] nums, int val) {int slow = 0;for (int fast = 0; fast < nums.length; fast++) {if (nums[fast] != val) {nums[slow++] = nums[fast];}}return slow;
}
方法二实现代码
public int removeElement(int[] nums, int val) {int index = 0;for (int num : nums) {if (num != val) {nums[index++] = num;}}return index;
}
方法三实现代码
public int removeElement(int[] nums, int val) {int left = 0;int right = nums.length - 1;while (left <= right) {if (nums[left] == val) {nums[left] = nums[right];right--;} else {left++;}}return left;
}
4. 复杂度分析
时间复杂度分析
三种方法的时间复杂度均为 O(n),其中 n 为数组的长度,因为需要遍历整个数组。
空间复杂度分析
三种方法的空间复杂度均为 O(1),因为只使用了常数个额外变量。
5. 测试与验证
测试用例设计
- 输入数组为空
- 输入数组中不存在给定值
- 输入数组中所有元素均为给定值
- 输入数组中部分元素为给定值
测试结果分析
根据不同的测试用例,分析三种方法的输出结果,验证算法的正确性。
6. 扩展
如何处理特殊情况和边界条件?
- 考虑输入数组为空的情况,直接返回 0。
- 考虑输入数组中不存在给定值的情况,直接返回原数组的长度。
- 考虑输入数组中所有元素均为给定值的情况,直接返回 0。
如何优化算法以提高执行效率?
- 方法一和方法二的效率相似,但方法一更加简洁易懂,方法二可以省略下标遍历。
- 方法三在交换时可以减少元素移动次数,提高效率。
如何处理数组中可能存在的重复元素?
- 可以根据需要选择保留或跳过重复元素。
7. 总结
移除元素问题是一个经典的数组操作问题,通过三种不同的解题思路和算法实现,可以有效地移除数组中指定的元素,并返回新数组的长度。通过本文的详细讲解,读者可以更好地理解这个问题,掌握解题的关键思路和技巧。
8. 参考文献
- LeetCode 官方网站
- 《算法导论》
- 《程序员面试金典》
感谢阅读
期待下一篇…
相关文章:

力扣经典150题第二题:移除元素
移除元素问题详解与解决方法 1. 介绍 移除元素问题是 LeetCode 经典题目之一,要求原地修改输入数组,移除所有数值等于给定值的元素,并返回新数组的长度。 问题描述 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等…...

55555555555555
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和…...
:图像形态学处理(上))
用Skimage学习数字图像处理(018):图像形态学处理(上)
本节开始讨论图像形态学处理,这是上篇,将介绍与二值形态学相关的内容,重点介绍两种基本的二值形态学操作:腐蚀和膨胀,以及三种复合二值形态学操作:开、闭和击中击不中变换。 目录 9.1 基础 9.2 基本操作…...

MySQL中 in 和 exists 区别
在MySQL中,IN和EXISTS都是用于在子查询中测试条件的操作符,但它们在处理和效率上有一些重要的区别。MySQL中的in语句是把外表和内表作hash连接,⽽exists语句是对外表作loop循环,每次loop循环再对内表进⾏查询。⼤家⼀直认为exists…...

Java基础 - 代码练习
第一题:集合的运用(幸存者) public class demo1 {public static void main(String[] args) {ArrayList<Integer> array new ArrayList<>(); //一百个囚犯存放在array集合中Random r new Random();for (int i 0; i < 100; …...
【Redis】redis集群模式
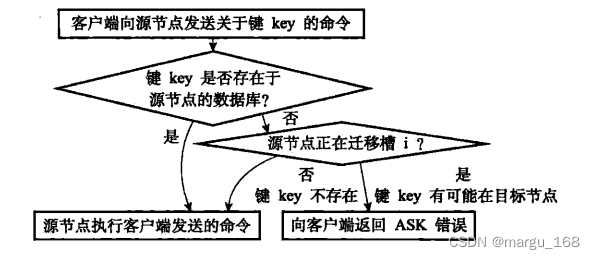
概述 Redis集群,即Redis Cluster,是Redis 3.0开始引入的分布式存储方案。实际使用中集群一般由多个节点(Node)组成,Redis的数据分布在这些节点中。集群中的节点分为主节点和从节点:只有主节点负责读写请求和集群信息的维护&#…...

基于opencv的猫脸识别模型
opencv介绍 OpenCV的全称是Open Source Computer Vision Library,是一个跨平台的计算机视觉库。OpenCV是由英特尔公司发起并参与开发,以BSD许可证授权发行,可以在商业和研究领域中免费使用。OpenCV可用于开发实时的图像处理、计算机视觉以及…...

基于注意力整合的超声图像分割信息在乳腺肿瘤分类中的应用
基于注意力整合的超声图像分割信息在乳腺肿瘤分类中的应用 摘要引言方法 Segmentation information with attention integration for classification of breast tumor in ultrasound image 摘要 乳腺癌是世界范围内女性最常见的癌症之一。基于超声成像的计算机辅助诊断&#x…...
数据库重点知识(个人整理笔记)
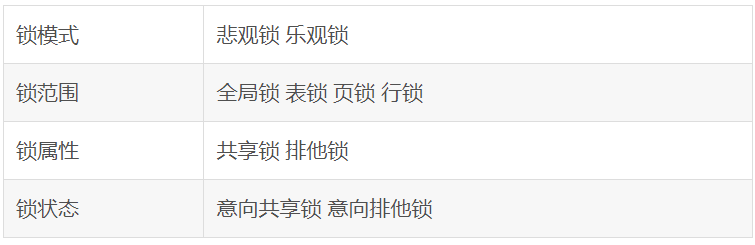
目录 1. 索引是什么? 1.1. 索引的基本原理 2. 索引有哪些优缺点? 3. MySQL有哪几种索引类型? 4. mysql聚簇和非聚簇索引的区别 5. 非聚簇索引一定会回表查询吗? 6. 讲一讲前缀索引? 7. 为什么索引结构默认使用B…...

[技术闲聊]checklist
电路设计完成后,需要确认功能完整性,明确是否符合设计规格需求;需要确认电路设计是否功能符合但是系列项不符合设计规则,如果都没有问题,那么就可以发给layout工程师。 今天主要讲讲电路设计规则,涉及到一…...
力扣刷题 二叉树的迭代遍历
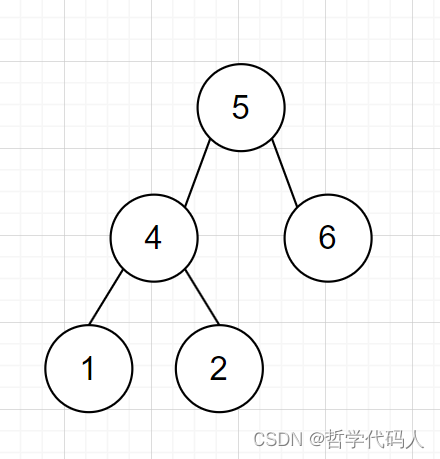
题干 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root [1,null,2,3] 输出:[1,2,3]示例 2: 输入:root [] 输出:[]示例 3: 输入:root [1] 输…...
【二】Django小白三板斧
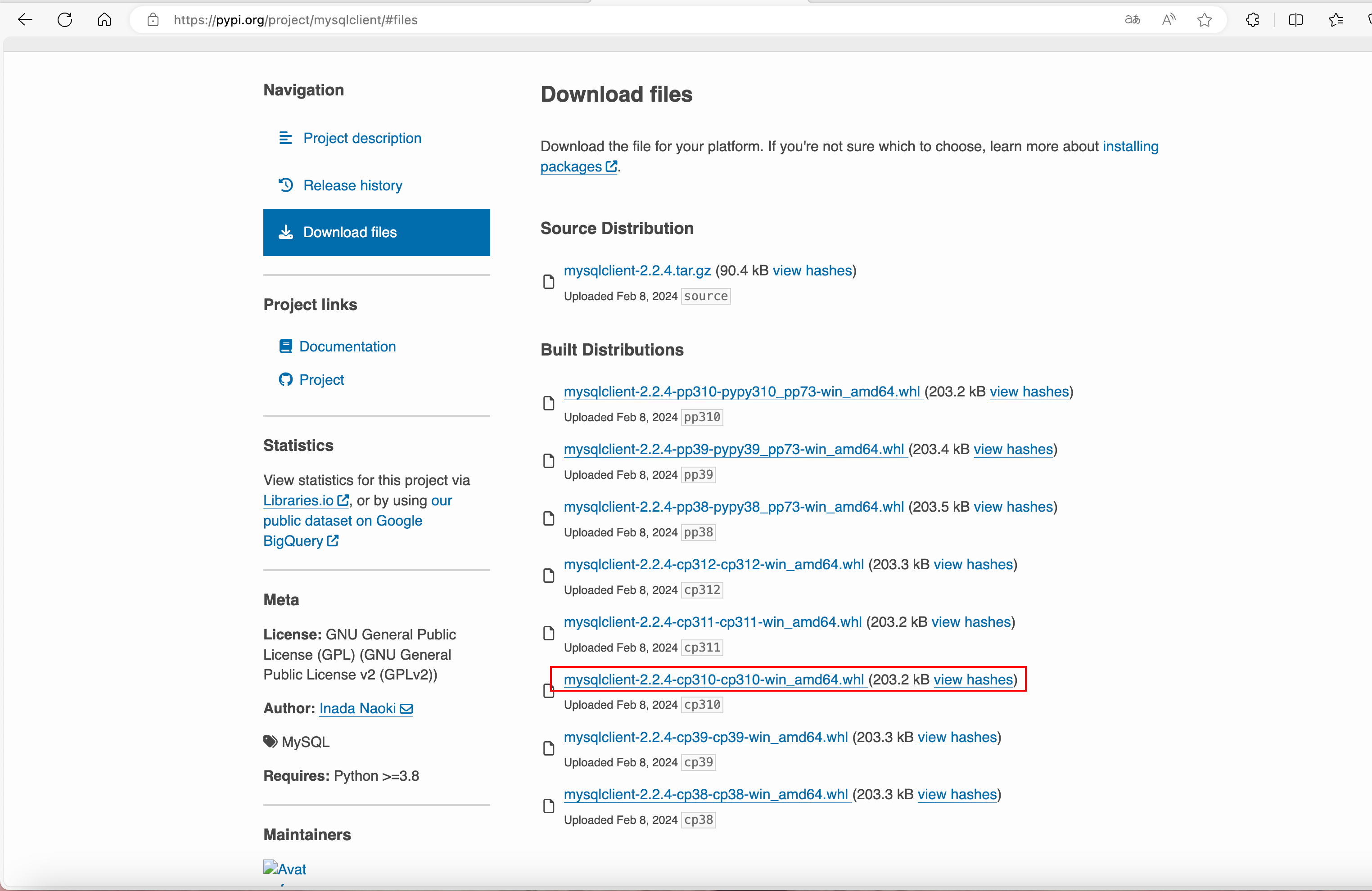
今日内容 静态文件配置 request对象方法初识 pycharm链接数据库(MySQL) django链接数据库(MySQL) Django ORM简介 利用ORM实现数据的增删查改 【一】Django小白三板斧 HttpResponse 返回字符串类型的数据 render 返回HTML文…...
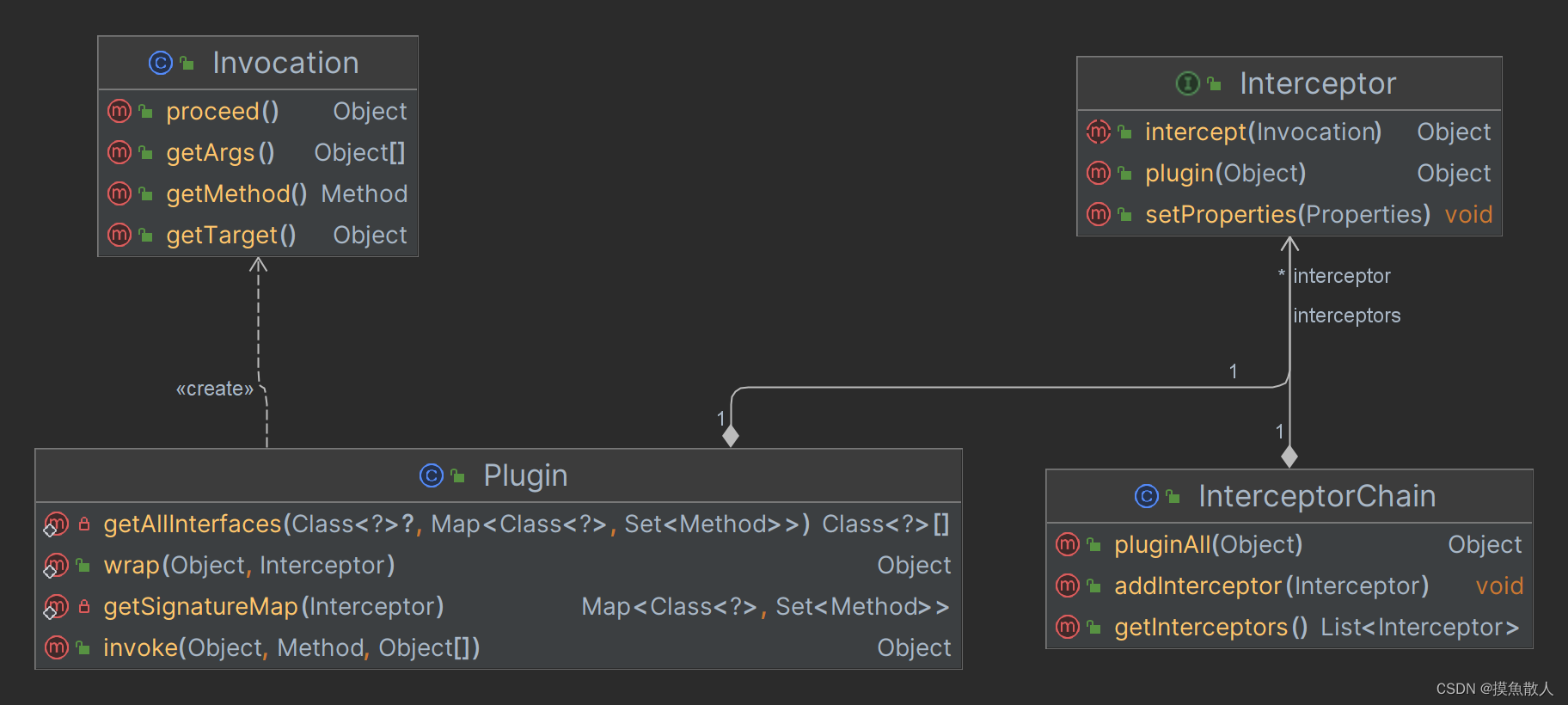
MyBatis的基本应用
源码地址 01.MyBatis环境搭建 添加MyBatis的坐标 <!--mybatis坐标--><dependency><groupId>org.mybatis</groupId><artifactId>mybatis</artifactId><version>3.5.9</version></dependency><!--mysql驱动坐…...
Day80:服务攻防-中间件安全HW2023-WPS分析WeblogicJettyJenkinsCVE
目录 中间件-Jetty-CVE&信息泄漏 CVE-2021-34429(信息泄露) CVE-2021-28169(信息泄露) 中间件-Jenkins-CVE&RCE执行 cve_2017_1000353 CVE-2018-1000861 cve_2019_1003000 中间件-Weblogic-CVE&反序列化&RCE 应用金山WPS-HW2023-RCE&复现&上线…...

使用generator实现async函数
我们先来看一下async函数是怎么使用的 const getData (sec) > new Promise((resolve) > {setTimeout(() > resolve(sec * 2), sec * 1000);})// aim to get this asycnFun by generator async function asyncFun() {const data1 await getData(1);const data2 awa…...

go并发请求url
sync.WaitGroup写法 package mainimport ("database/sql""fmt""net/http""sync""time"_ "github.com/go-sql-driver/mysql" )func main() {//开始计时start : time.Now()//链接数据库,用户名…...
刷题之Leetcode704题(超级详细)
704. 二分查找 力扣题目链接(opens new window)https://leetcode.cn/problems/binary-search/ 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标&am…...

leetcode热题100.前k个高频元素
作者:晓宜 🌈🌈🌈 个人简介:互联网大厂Java准入职,阿里云专家博主,csdn后端优质创作者,算法爱好者 ❤️❤️❤️ 你的关注是我前进的动力😊 Problem: 347. 前 K 个高频元…...

LangChain Demo | Agent X ReAct X wikipedia 询问《三体》的主要内容
背景 LangChain学习中,尝试改了一下哈里森和吴恩达课程当中的问题,看看gpt-3.5-turbo在集成了ReAct和wikipedia后,如何回答《三体》的主要内容是什么这个问题,当然,主要是为了回答这问题时LangChain内部发生了什么。所…...
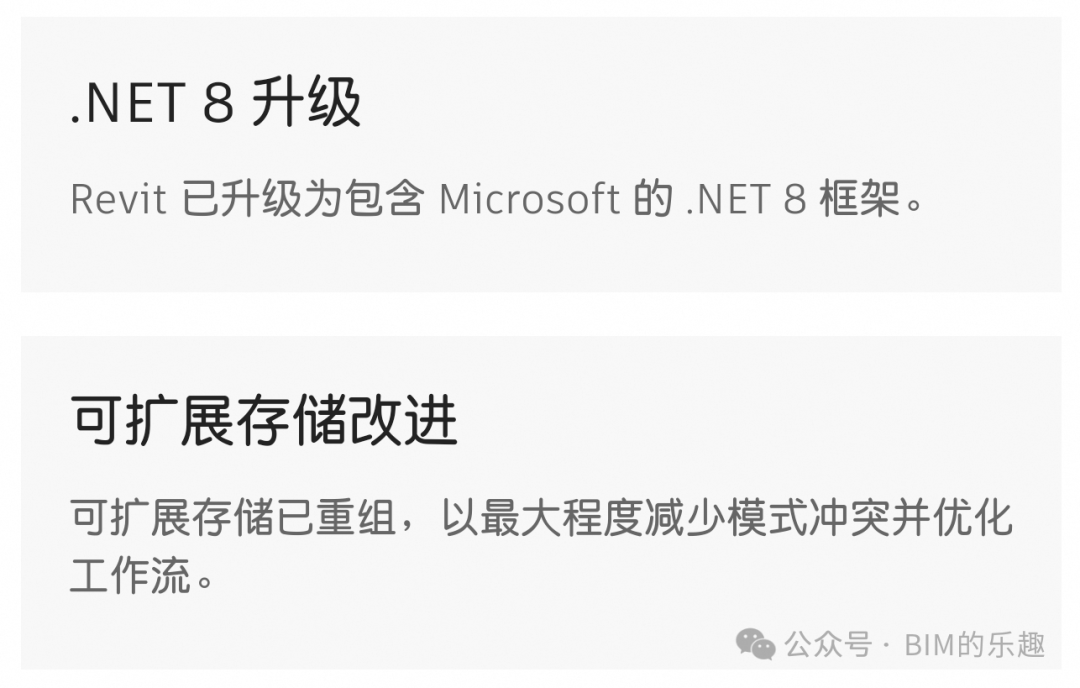
Revit 2025新功能一览~
Hello大家好!我是九哥~ Revit2025已经更新,安装后,简单试了下,还是挺不错的,流畅度啊,新功能啊,看来还是有听取用户意见的,接下来就简单看看都有哪些新功能。 好了,今天的…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
