【NC50937】货仓选址
题目
货仓选址
二分,前缀和,数学推导
思路
由题意可知货仓的位置是可以和商店的位置重合的。首先应该将商店的坐标从小到大排序,然后假设商店的坐标为 a i a_i ai,货仓的坐标为 x x x,货仓左侧第一家商店(可能和货仓重合)的坐标为 a k a_k ak,则由题意计算出的距离应该为:
d i s t = ∑ i = 0 k ( x − a i ) + ∑ i = k + 1 n − 1 ( a i − x ) = ( k + 1 ) x − ∑ i = 0 k a i + ∑ i = k + 1 n − 1 a i − ( n − 1 − k ) x dist=\sum_{i=0}^k(x-a_i)+\sum_{i=k+1}^{n-1}(a_i-x)=(k+1)x-\sum_{i=0}^ka_i+\sum_{i=k+1}^{n-1}a_i-(n-1-k)x dist=i=0∑k(x−ai)+i=k+1∑n−1(ai−x)=(k+1)x−i=0∑kai+i=k+1∑n−1ai−(n−1−k)x
根据上面的推导最直观的思路就是枚举从 a 0 → a i a_0\to a_i a0→ai 的所有坐标,然后老老实实地计算每个 d i s t dist dist 取最小值,这种思路需要用到二分,具体见代码。
这里要记录的并不是像上面那样简单模拟的思路,而是更为巧妙一些的:
假设给出的商店坐标(排好序之后)为 1 , 2 , 6 , 9 1,2,6,9 1,2,6,9
则按上面模拟的思路计算可得:
| 货仓位置 | 距离 |
|---|---|
| 1 | 14 |
| 2 | 12 |
| 3 | 12 |
| 4 | 12 |
| 5 | 12 |
| 6 | 12 |
| 7 | 14 |
| 8 | 16 |
| 9 | 18 |
为什么不枚举小于 a 0 a_0 a0 和大于 a n a_n an 的位置呢?这个问题留给读者。
由上面的表格可以得出,似乎越往商店的中部位置靠近,距离就越短。
不妨直接研究中部的商店,这里的商店数是偶数个,则研究中间的两个商店,我们会得到一个有趣的结论:
在中部的两个商店之间建立货仓的话,各商店到货仓的距离是不变的,并且距离为两两对称的商店之间的距离之和,比如例子里面的距离就是 6 − 2 + 9 − 1 = 12 6-2+9-1=12 6−2+9−1=12。
所以这题可以直接求两两对称商店的距离之差的和即可,奇数个商店数就将货仓建立在最中间的商店处即可。具体的证明这里不做记录,但是是很容易想通的。
代码
代码一:二分模拟
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
typedef long long LL;int cmp(const void* a, const void* b) { return *(int*)a - *(int*)b; }// 寻找第一个小于等于 target 的元素的下标,没有则返回 -1
int first_le(int* arr, int n, int target) {int l = 0, r = n - 1, mid = 0;while (l <= r) {mid = l + ((r - l) >> 1);if (arr[mid] <= target) {if (mid == n - 1 || arr[mid + 1] > target) {return mid;}l = mid + 1;} else {r = mid - 1;}}return -1;
}int main(void) {int n = 0;scanf("%d", &n);int a[n], i = 0;for (i = 0; i < n; i++) {scanf("%d", a + i);}qsort(a, n, sizeof(int), cmp);LL sum[n], ans = LLONG_MAX, t = 0;sum[0] = a[0];for (i = 1; i < n; i++) {sum[i] = sum[i - 1] + a[i];}for (LL x = a[0]; x <= a[n - 1]; x++) {i = first_le(a, n, x);t = (i + 1) * x - sum[i] + sum[n - 1] - sum[i] - (n - 1 - i) * x;if (t < ans) ans = t;}printf("%lld\n", ans);return 0;
}
代码二:数学推导
#include <stdio.h>
#include <stdlib.h>#define N 1000005typedef long long LL;int cmp(const void* a, const void* b) { return *(int*)a - *(int*)b; }int main(void) {int n = 0;scanf("%d", &n);int a[n], i = 0;LL ans = 0;for (i = 0; i < n; i++) {scanf("%d", a + i);}qsort(a, n, sizeof(int), cmp);for (i = n >> 1; i < n; i++) {ans += a[i] - a[n - i - 1];}printf("%lld\n", ans);return 0;
}
相关文章:

【NC50937】货仓选址
题目 货仓选址 二分,前缀和,数学推导 思路 由题意可知货仓的位置是可以和商店的位置重合的。首先应该将商店的坐标从小到大排序,然后假设商店的坐标为 a i a_i ai,货仓的坐标为 x x x,货仓左侧第一家商店&#x…...

Nginx配置使用笔记
Nginx配置使用笔记 前言 官网下载压缩包https://nginx.org/ 解压完成后当前目录cmd输入nginx指令启动 访问http://localhost:80确认启动成功 1.部署前端项目 部署前端项目到路径E:\Workspaces\Vscode\app-web 2.0配置nginx.conf文件 在nginx安装的conf目录下新建一个文件夹l…...
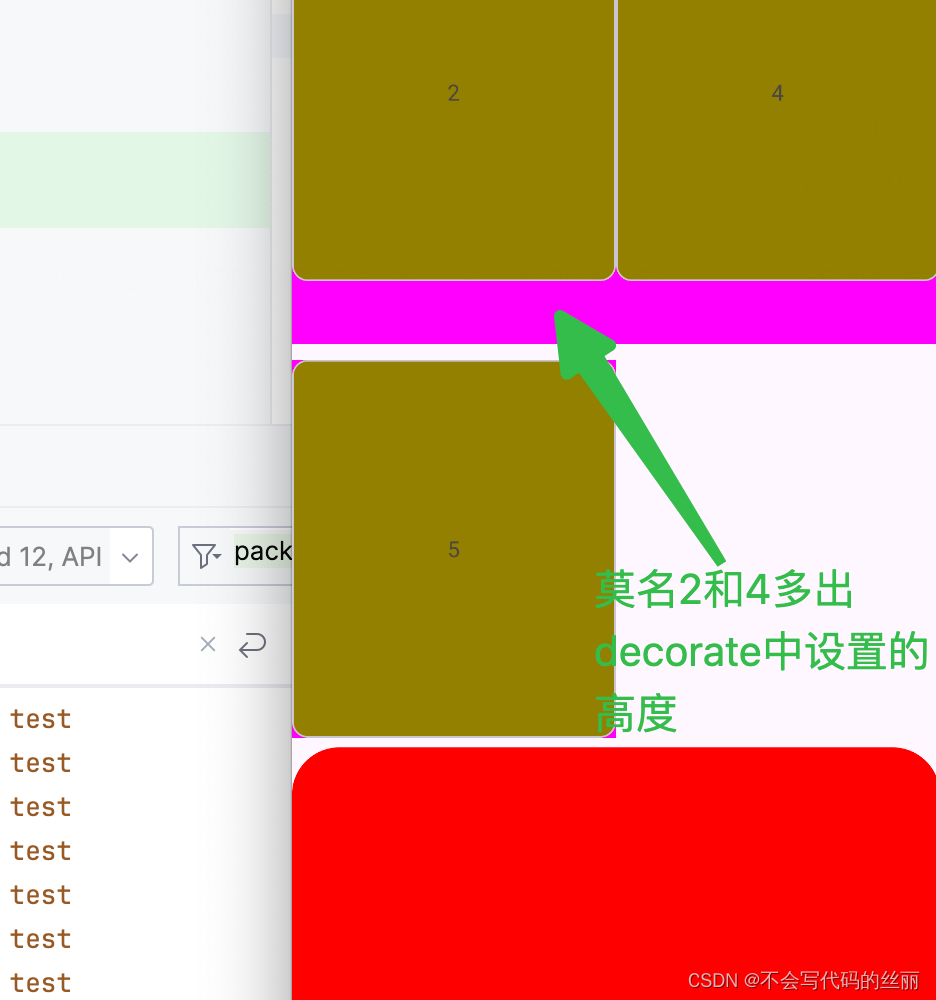
GridLayoutManager 中的一些坑
前言 如果GridLayoutManager使用item的布局都是wrap_cotent 那么会在布局更改时会出现一些出人意料的情况。(本文完全不具备可读性和说教性,仅为博主方便查找问题) 布局item: <!--layout_item.xml--> <?xml version"1.0&qu…...

算法实验二 矩阵最小路径和 LIS
算法实验课二 矩阵最小路径和 leetcode裸题 最小路径和 给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。 示例 1: 输入&…...
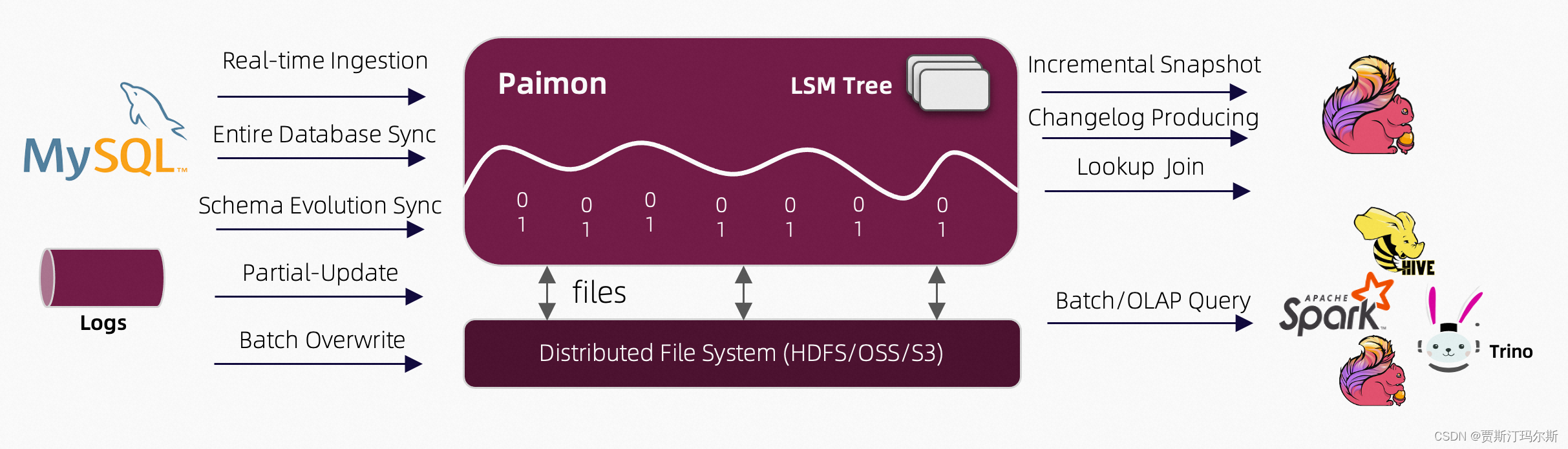
Apache Paimon实时数据糊介绍
Apache Paimon 是一种湖格式,可以使用 Flink 和 Spark 构建实时 数据糊 架构,用于流式和批处理操作。Paimon 创新地将湖格式和 LSM(日志结构合并树)结构相结合,将实时流式更新引入湖架构中。 Paimon 提供以下核心功能: 实时更新: 主键表支持大规模更新的写入,具有非常…...
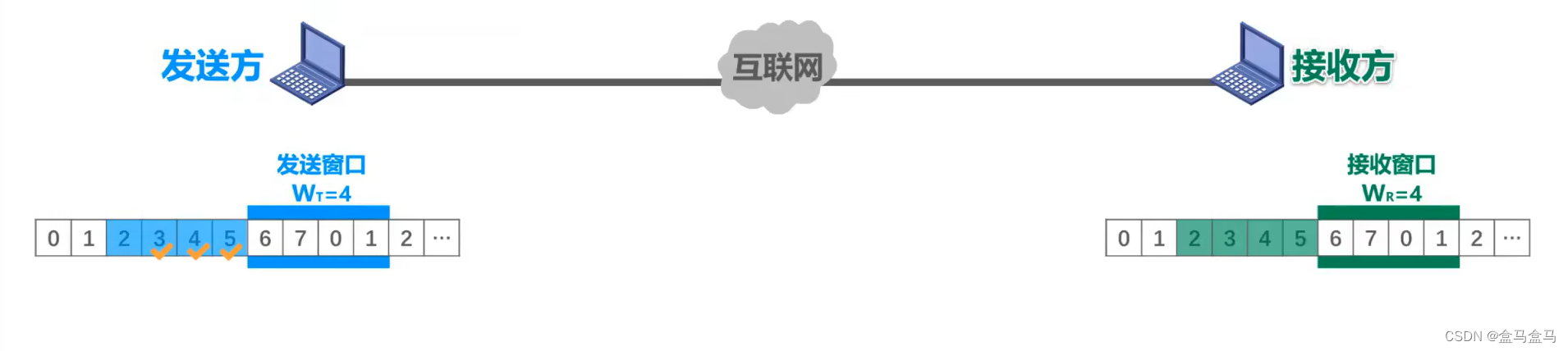
计算机网络:数据链路层 - 可靠传输协议
计算机网络:数据链路层 - 可靠传输协议 可靠传输概念停止-等待协议 SW回退N帧协议 GBN选择重传协议 SR 可靠传输概念 如下所示,帧在传输过程中受到干扰,产生了误码。接收方的数据链路层,通过真伪中的真检验序列 FCS 字段的值&…...

苍穹外卖07(缓存菜品,SpringCache,缓存套餐,添加购物车菜品和套餐多下单,查看购物车,清除购物车,删除购物车中一个商品)
目录 一、缓存菜品 1 问题说明 2 实现思路 3 代码开发:修改DishServiceImpl 4 功能测试 二、SpringCache 1. 介绍 2. 使用语法 1 起步依赖 2 使用要求 3 常用注解 4 SpEL表达式(了解备用) 5 步骤小结 3.入门案例 1 准备环境 2 使用入门 1 引导类上加…...

C语言第三十八弹---编译和链接
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 编译和链接 1、翻译环境和运行环境 2、翻译环境 2.1、预处理(预编译) 2.2、编译 2.2.1、词法分析 2.2.2、语法分析 2.2.3、语义分…...

无人售货奶柜:开启便捷生活的新篇章
无人售货奶柜:开启便捷生活的新篇章 在这个快节奏的现代生活中,科技的革新不仅为我们带来了前所未有的便利,更在不经意间改变着我们的日常。其中,无人售货技术的出现,尤其是无人售货奶柜,已经成为我们生活…...

STM32为什么不能跑Linux?
STM32是一系列基于ARM Cortex-M微控制器的产品,它们主要用于嵌入式系统中。而Linux则是一个开源的类Unix操作系统,主要面向的是桌面电脑、服务器等资源丰富的计算机。虽然理论上可以将Linux移植到STM32上运行,但是由于两者之间存在着很多技术…...
—Dubbo服务引用源码(1))
Dubbo 3.x源码(18)—Dubbo服务引用源码(1)
基于Dubbo 3.1,详细介绍了Dubbo服务的发布与引用的源码。 此前我们学习了Dubbo的服务导出的源码,在DubboBootstrapApplicationListener#startSync方法中,在调用了exportServices方法进行服务导出之后,立即调用了referServices方法…...

设计模式:工厂模式和抽象工厂模式的区别
定义 工厂模式(Factory Pattern)通常指的是工厂方法模式(Factory Method Pattern),它定义了一个创建对象的方法,由子类决定要实例化的类。工厂方法让类的实例化推迟到子类。 抽象工厂模式(Abstract Factory Pattern)提供了一个接口,用于创建相关或依赖对象的家族,而…...
)
python面试题(36~50)
36、如何取一个整数的绝对值? 这可以通过abs函数来实现。 abs(2) #> 2 abs(-2) #> 2 37、如何将两个列表组合成一个元组列表? 可以使用zip函数将列表组合成一个元组列表。这不仅仅限于使用两个列表。也适合3个或更多列表的情况。 a [a,b,c] b [1,2,3] [(k,v) fo…...
Vue 样式技巧总结与整理[中级局]
SFC(单文件组件)由 3 个不同的实体组成:模板、脚本和样式。三者都很重要,但后者往往被忽视,即使它可能变得复杂,且经常导致挫折和 bug。 更好的理解可以改善代码审查并减少调试时间。 这里有 7 个奇技淫巧…...
cesium加载.tif格式文件
最近项目中有需要直接加载三方给的后缀名tif格式的文件 <script src"https://cdn.jsdelivr.net/npm/geotiff"></script> 或者 yarn add geotiff npm install geotiff 新建tifs.js import GeoTIFF, { fromBlob, fromUrl, fromArrayBuffer } from geotif…...
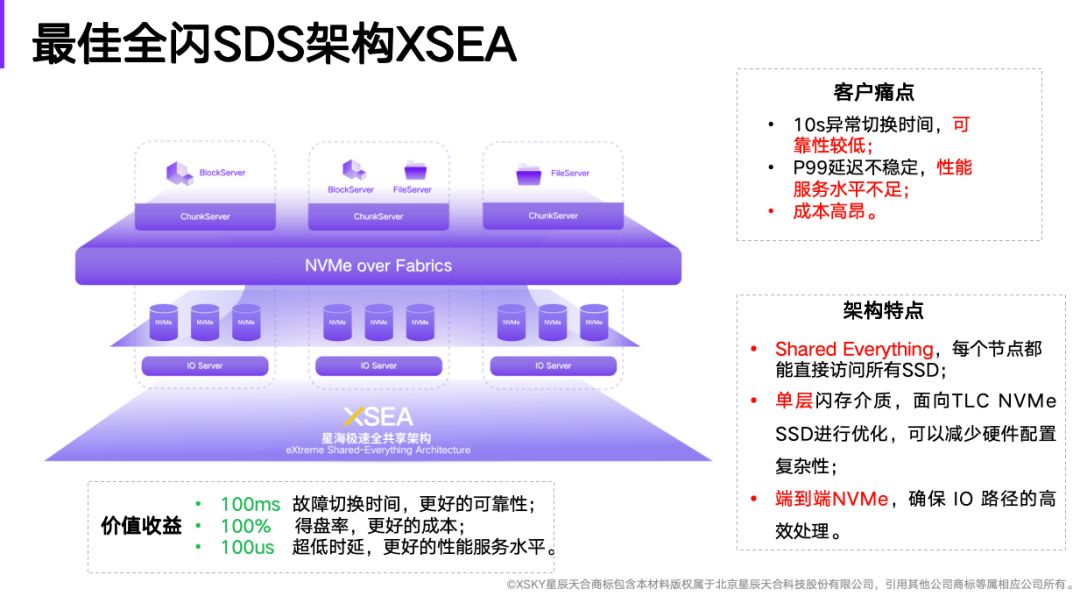
分布式全闪占比剧增 152%,2023 年企业存储市场报告发布
近日,IDC 发布了 2023 年度的中国存储市场报告。根据该报告,在 2023 年软件定义存储的市场占比进一步扩大,分布式全闪的增长尤其亮眼,其市场份额从 2022 年的 7% 剧增到 2023 年的 17.7%,增长了 152%。 01 中国企业存…...
双链表 模板))
LeetCode 707. 设计链表(单链表、(非循环)双链表 模板)
你可以选择使用单链表或者双链表,设计并实现自己的链表。 单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。 如果是双向链表,则还需要属性 prev 以指示链表中的上一个节点…...

深入了解Flutter中Overlay的介绍以及使用
Flutter Overlay 介绍 在 Flutter 中,Overlay 是一种特殊的 Widget,它可以用来在应用程序的其他部分之上显示内容。Overlay 非常适合用于显示模态对话框、弹出菜单、工具提示等。 Overlay 的工作原理 Overlay 位于 Flutter 的渲染树之外,这…...

文本直接生成2分钟视频,即将开源模型StreamingT2V
Picsart人工智能研究所、德克萨斯大学和SHI实验室的研究人员联合推出了StreamingT2V视频模型。通过文本就能直接生成2分钟、1分钟等不同时间,动作一致、连贯、没有卡顿的高质量视频。 虽然StreamingT2V在视频质量、多元化等还无法与Sora媲美,但在高速运…...

时序预测 | Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测
时序预测 | Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测 目录 时序预测 | Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测(完整源码…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
