马尔可夫决策过程
1. 马尔可夫决策过程
马尔可夫决策过程不过是引入"决策"的马氏过程.
Pij(a)=P{Xn+1=j∣X0,a0,X1,a1,...,Xn=i,an=1}=P{Xnn+1=j∣Xn=i,an=a}\begin{split} P_{ij}(a) &= P\{X_{n+1} = j|X_0, a_0, X_1, a_1, ..., X_n = i, a_n = 1\} \\ &=P\{X_n{n+1} = j|X_n = i, a_n = a\} \end{split} Pij(a)=P{Xn+1=j∣X0,a0,X1,a1,...,Xn=i,an=1}=P{Xnn+1=j∣Xn=i,an=a}
状态转移家族很取决于XnX_nXn和ana_nan.
引入"随机化"的策略(policy)----------β⃗\vec{\beta}β, 就是所谓的"因时制宜".
β⃗={βi(a),a∈A,i=1,2,...M}\vec{\beta} = \{\beta_i(a),\ a\in A, i = 1,2,...M \} β={βi(a), a∈A,i=1,2,...M}
AAA表示行动集, "智能体"从行动集中选取其中一个元素/行动.
对于某个特定的βi(a)\beta_i(a)βi(a), 其意义为: 在状态iii下, 选取行动aaa的概率.
易知
{0≤βi(a)≤1∀i,a∑aβi(a)=1∀i\begin{cases} 0 \leq\beta_i(a) \leq 1 \ \ \ \ \ &\forall i,a \\ \sum \limits_a \beta_i(a) = 1 &\forall i \end{cases} ⎩⎨⎧0≤βi(a)≤1 a∑βi(a)=1∀i,a∀i
所以对于某个策略β⃗\vec{\beta}β下的MDP, 相应的状态转移概率可以表示如下:
Pij(β⃗)=Pβ⃗{Xn+1=j∣Xn=i}=∑aPij(a)βi(a)\begin{split} P_{ij}(\vec{\beta}) &= P_{\vec{\beta}}\{X_{n+1} = j|X_n = i\} \\ &=\sum \limits_a P_{ij}(a)\beta_i(a) \end{split} Pij(β)=Pβ{Xn+1=j∣Xn=i}=a∑Pij(a)βi(a)
从这一状态转移概率的表达式, 可以很清楚地看到MDP和MP的不同:
马氏链的状态转移概率是一个单纯的数, 而MDP的状态转移概率不仅有一个"策略"的前提, 而且是一个加权和, 一个不同行动下, i到j的状态转移概率的加权和, 权重就是( 给定策略β⃗\vec{\beta}β下 )选取行动aaa的概率βi(a)\beta_i(a)βi(a).
假设对于任意的策略β⃗\vec{\beta}β, 所导致的马氏链{Xn,n=0,1,...}\{X_n, n=0,1,...\}{Xn,n=0,1,...}都是各态历经的(ergodic).
下面我们来证明MDP中最重要的一个命题.
对于任意策略β⃗\vec{\beta}β, 记πia\pi_{ia}πia为, “给定策略β⃗\vec{\beta}β下, 稳态情形时(n→∞)(n\rightarrow \infin)(n→∞)MDP既处于状态iii又采取了行动aaa的概率”, 即
πia=limn→∞Pβ⃗{Xn=i,an=a}\pi_{ia} = \lim _{n\rightarrow \infin} P_{\vec{\beta}}\{X_n = i, a_n = a\} πia=n→∞limPβ{Xn=i,an=a}
易知π⃗=(πia)\vec{\pi} = (\pi_{ia})π=(πia)是一个类似表示概率分布的东西(分布向量或者分布矩阵), 而且对于π⃗\vec{\pi}π, 必须满足:
{πia≥0,∀i,a∑i∑aπia=1∑aπja=∑i∑a′πia′Pij(a′)∀j\begin{cases} \pi_{ia} \geq 0, \ \forall i, a \\ \sum \limits_i \sum \limits_a \pi_{ia} = 1 \\ \sum \limits_a \pi_{ja} = \sum \limits_i \sum \limits_{a'} \pi_{ia'}P_{ij}(a') \ \forall j \end{cases} ⎩⎨⎧πia≥0, ∀i,ai∑a∑πia=1a∑πja=i∑a′∑πia′Pij(a′) ∀j
三个条件对应的方程, 其物理含义都是显然的, 其中, 第三个条件方程的左边代表稳态时MDP处于状态jjj的概率, 而等式右边则是状态jjj对应的"切面包定理".
因此, 我们我们可以说, 在MDP中, 对于任意一个策略β⃗\vec{\beta}β, 都会存在某个满足上述三个条件的概率分布向量π⃗\vec{\pi}π.
但是, 反过来也是成立的:
对于任意一个(二维)概率分布向量π⃗,如果该向量满足上述三个条件,则必然存在一个策略为β⃗的马尔科夫决策过程,使得稳态时,其既处于状态i又采取了行动a的概率恰好等于πia\begin{split} &对于任意一个(二维)概率分布向量\vec{\pi}, 如果该向量满足上述三个条件, 则必然存在\\ &一个策略为\vec{\beta}的马尔科夫决策过程, 使得稳态时, 其既处于状态i又采取了行动a的\\ &概率恰好等于\pi_{ia} \end{split} 对于任意一个(二维)概率分布向量π,如果该向量满足上述三个条件,则必然存在一个策略为β的马尔科夫决策过程,使得稳态时,其既处于状态i又采取了行动a的概率恰好等于πia
证明这一反命题的思路, 是要构造那个策略β⃗\vec{\beta}β, 这个策略肯定不是凭空产生的, 而是要根据上述三个条件, 和从马氏链的性本身入手.
我们先形式地写出一个MDP, 和一个策略β⃗\vec{\beta}β.
我们将该MDP使用策略β⃗\vec{\beta}β的稳态情形时, 既处于状态iii又采取了行动aaa的概率记为PiaP_{ia}Pia.
如果策略β⃗\vec{\beta}β真的存在, Pia=πiaP_{ia} = \pi_{ia}Pia=πia就会成立.
我们先看看PiaP_{ia}Pia满足什么样的性质.
易知
{Pia≥0,∀i,a∑i∑aPia=1Pja=∑i∑a′Pia′Pij(a′)βj(a)\begin{cases} P_{ia} \geq 0 , \ \forall i, a \\ \sum \limits_i \sum \limits_a P_{ia} = 1 \\ P_{ja} = \sum \limits_i \sum \limits_{a'} P_{ia'}P_{ij}(a')\beta_j(a) \end{cases} ⎩⎨⎧Pia≥0, ∀i,ai∑a∑Pia=1Pja=i∑a′∑Pia′Pij(a′)βj(a)
第三个式子的推导过程如下
Pja=limn→∞Pβ⃗{Xn+1=j,an+1=a}=limn→∞∑i,a′Pβ⃗{Xn+1=j,an+1=a∣Xn=i,an=a′}Pβ⃗{Xn=i,an=a′}=limn→∞∑i,a′Pβ⃗{Xn+1=j,an+1=a∣Xn=i,an=a′}Pia′=limn→∞∑i,a′Pβ⃗{an+1=a∣Xn+1=j,Xn=i,an=a′}Pβ⃗{Xn+1=j∣Xn=i,an=a′}Pia′=limn→∞∑i,a′Pβ⃗{an+1=a∣Xn+1=j}Pβ⃗{Xn+1=j∣Xn=i,an=a′}Pia′=∑i,a′βj(a)Pij(a′)Pia′=∑i∑a′Pia′Pij(a′)βj(a)\begin{split} P_{ja} &= \lim _{n\rightarrow \infin} P_{\vec{\beta}}\{X_{n+1} = j, a_{n+1} = a\} \\ &=\lim _{n\rightarrow \infin} \sum \limits_{i,a'}P_{\vec{\beta}}\{X_{n+1} = j, a_{n+1} = a|X_n = i, a_n = a'\}P_{\vec{\beta}}\{X_{n} = i, a_{n} = a'\} \\ &=\lim _{n\rightarrow \infin} \sum \limits_{i,a'}P_{\vec{\beta}}\{X_{n+1} = j, a_{n+1} = a|X_n = i, a_n = a'\}P_{ia'} \\ &=\lim _{n\rightarrow \infin} \sum \limits_{i,a'}P_{\vec{\beta}}\{ a_{n+1} = a|X_{n+1} = j,X_n = i, a_n = a'\}P_{\vec{\beta}}\{X_{n+1} = j|X_n = i, a_n = a'\}P_{ia'} \\ &=\lim _{n\rightarrow \infin} \sum \limits_{i,a'}P_{\vec{\beta}}\{ a_{n+1} = a|X_{n+1} = j\}P_{\vec{\beta}}\{X_{n+1} = j|X_n = i, a_n = a'\}P_{ia'} \\ &= \sum \limits_{i,a'}\beta_j(a) P_{ij}(a') P_{ia'} \\ &=\sum \limits_i \sum \limits_{a'} P_{ia'}P_{ij}(a')\beta_j(a) \end{split} Pja=n→∞limPβ{Xn+1=j,an+1=a}=n→∞limi,a′∑Pβ{Xn+1=j,an+1=a∣Xn=i,an=a′}Pβ{Xn=i,an=a′}=n→∞limi,a′∑Pβ{Xn+1=j,an+1=a∣Xn=i,an=a′}Pia′=n→∞limi,a′∑Pβ{an+1=a∣Xn+1=j,Xn=i,an=a′}Pβ{Xn+1=j∣Xn=i,an=a′}Pia′=n→∞limi,a′∑Pβ{an+1=a∣Xn+1=j}Pβ{Xn+1=j∣Xn=i,an=a′}Pia′=i,a′∑βj(a)Pij(a′)Pia′=i∑a′∑Pia′Pij(a′)βj(a)
对比上下的三条件方程组:
{πia≥0,∀i,a∑i∑aπia=1∑aπja=∑i∑a′πia′Pij(a′)∀j\begin{cases} \pi_{ia} \geq 0, \ \forall i, a \\ \sum \limits_i \sum \limits_a \pi_{ia} = 1 \\ \sum \limits_a \pi_{ja} = \sum \limits_i \sum \limits_{a'} \pi_{ia'}P_{ij}(a') \ \forall j \end{cases} ⎩⎨⎧πia≥0, ∀i,ai∑a∑πia=1a∑πja=i∑a′∑πia′Pij(a′) ∀j
和
{Pia≥0,∀i,a∑i∑aPia=1Pja=∑i∑a′Pia′Pij(a′)βj(a)\begin{cases} P_{ia} \geq 0 , \ \forall i, a \\ \sum \limits_i \sum \limits_a P_{ia} = 1 \\ P_{ja} = \sum \limits_i \sum \limits_{a'} P_{ia'}P_{ij}(a')\beta_j(a) \end{cases} ⎩⎨⎧Pia≥0, ∀i,ai∑a∑Pia=1Pja=i∑a′∑Pia′Pij(a′)βj(a)
易知, 求出策略β⃗\vec{\beta}β要在最后一个方程做文章.
将下面的方程组中的最后一个方程改为:
∑aPja=∑a∑i∑a′Pia′Pij(a′)βj(a)\sum \limits_aP_{ja} = \sum \limits_a \sum \limits_i \sum \limits_{a'} P_{ia'}P_{ij}(a')\beta_j(a) a∑Pja=a∑i∑a′∑Pia′Pij(a′)βj(a)
如果Pia=πiaP_{ia} = \pi_{ia}Pia=πia成立, 则应该有
∑aβj(a)=1\sum \limits_a \beta_j(a) = 1 a∑βj(a)=1
由βi(a)=P{β⃗选择a∣状态为i}\beta_i(a) = P\{\vec{\beta} 选择 a|状态为i\}βi(a)=P{β选择a∣状态为i}的物理意义, 且根据条件概率
P{β⃗选择a∣状态为i}=P{β⃗选择a且 状态为i}P{状态为i}=PiaP{状态为i}=Pia∑aP{状态为i∣(状态为i时)选择行动a}=Pia∑aPia\begin{split} P\{\vec{\beta} 选择 a|状态为i\} &= \frac{P\{\vec{\beta} 选择 a \ 且 \ 状态为i\}}{P\{状态为i\}} \\ &=\frac{P_{ia}}{P\{状态为i\}} \\ &=\frac{P_{ia}}{\sum \limits_{a} P\{状态为i|(状态为i时)选择行动a\}} \\ &=\frac{P_{ia}}{\sum \limits_{a}P_{ia}} \end{split} P{β选择a∣状态为i}=P{状态为i}P{β选择a 且 状态为i}=P{状态为i}Pia=a∑P{状态为i∣(状态为i时)选择行动a}Pia=a∑PiaPia
不难看出, 只要让策略β⃗\vec{\beta}β满足
βi(a)=πia∑aπia\beta_i(a) = \frac{\pi_{ia}}{\sum \limits_{a}\pi_{ia}} βi(a)=a∑πiaπia
即可. 这就证明了策略的存在性. 则就证明了命题.
这个命题的重要性, 在于去确定某种条件下最优的策略. 假定我们有一个MDP, 而且我们知道, 在处于状态iii时, 采取行动aaa能获得回报R(i,a)R(i, a)R(i,a), 则R(Xn,an)R(X_n, a_n)R(Xn,an)就是我们在nnn时刻所得到的收益.
则统计意义下, 给定策略β⃗\vec{\beta}β, MDP所进行的每一步的平均收益就是
Eβ⃗=limn→∞[∑i=1nR(Xi,ai)n]E_{\vec{\beta}} = \lim_{n\rightarrow \infin} \left[\frac{\sum \limits_{i=1}^{n}R(X_i ,a_i)}{n}\right] Eβ=n→∞limni=1∑nR(Xi,ai)
假设πia\pi_{ia}πia表示"给定策略β⃗\vec{\beta}β下, 稳态情形时(n→∞)(n\rightarrow \infin)(n→∞)MDP既处于状态iii又采取了行动aaa的概率", 则概率意义下, 稳态时MDP的平均收益为:
Eβ⃗=∑i∑aπiaR(i,a)E_{\vec{\beta}} = \sum \limits_i \sum \limits_{a} \pi_{ia}R(i, a) Eβ=i∑a∑πiaR(i,a)
我们上面的命题, 说明了策略和分布的等价性. 因此, 为了最大化每一步的平均收益而去选择一个最优策略β⃗∗\vec{\beta}^*β∗, 实际上等价于去寻找一个所谓的最优分布π⃗∗=(πia)∗\vec{\pi}^* = (\pi_{ia})^*π∗=(πia)∗.
该过程可以用一个优化问题表述:
maxπ⃗∑i∑aπiaR(i,a)s.t.πia≥0∑i∑aπia=1∑aπja=∑i∑a′πia′Pij(a′)∀j\begin{split} \max \limits_{\vec{\pi}} &\sum \limits_i \sum \limits_{a} \pi_{ia}R(i, a) \\ s. t.\ \ \ \ &\pi_{ia} \geq 0 \\ & \sum \limits_i \sum \limits_a \pi_{ia} = 1 \\ & \sum \limits_a \pi_{ja} = \sum \limits_i \sum \limits_{a'} \pi_{ia'}P_{ij}(a') \ \forall j \end{split} πmaxs.t. i∑a∑πiaR(i,a)πia≥0i∑a∑πia=1a∑πja=i∑a′∑πia′Pij(a′) ∀j
这是一个线性规划问题!
如果找到π⃗∗=(πia)∗\vec{\pi}^* = (\pi_{ia})^*π∗=(πia)∗, 则让
βi(a)∗=πia∗∑aπia∗\beta_i(a)^* = \frac{\pi_{ia}^*}{\sum \limits_{a}\pi_{ia}^*} βi(a)∗=a∑πia∗πia∗
即可.
相关文章:

马尔可夫决策过程
1. 马尔可夫决策过程 马尔可夫决策过程不过是引入"决策"的马氏过程. Pij(a)P{Xn1j∣X0,a0,X1,a1,...,Xni,an1}P{Xnn1j∣Xni,ana}\begin{split} P_{ij}(a) & P\{X_{n1} j|X_0, a_0, X_1, a_1, ..., X_n i, a_n 1\} \\ &P\{X_n{n1} j|X_n i, a_n a\} \e…...
win11下载配置CIC Flowmeter环境并提取流量特征
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、下载CIC Flowmeter二、安装java、maven、gradle和IDEA1.java 1.82.maven3.gradle4.IDEA三、CICFlowMeter-master使用四、流量特征1.含义2.获取前言 配了一整…...
JDK如何判断自己是什么公司的
0x00 前言 因为一些事情,遇到了这样一个问题,JDK如何判断自己是什么公司编译的。因为不同的公司编译出来,涉及到是否商用收费的问题。 平时自己使用的时候,是不会考虑到JDK的编译公司是哪一个,都是直接拿起来用&#…...
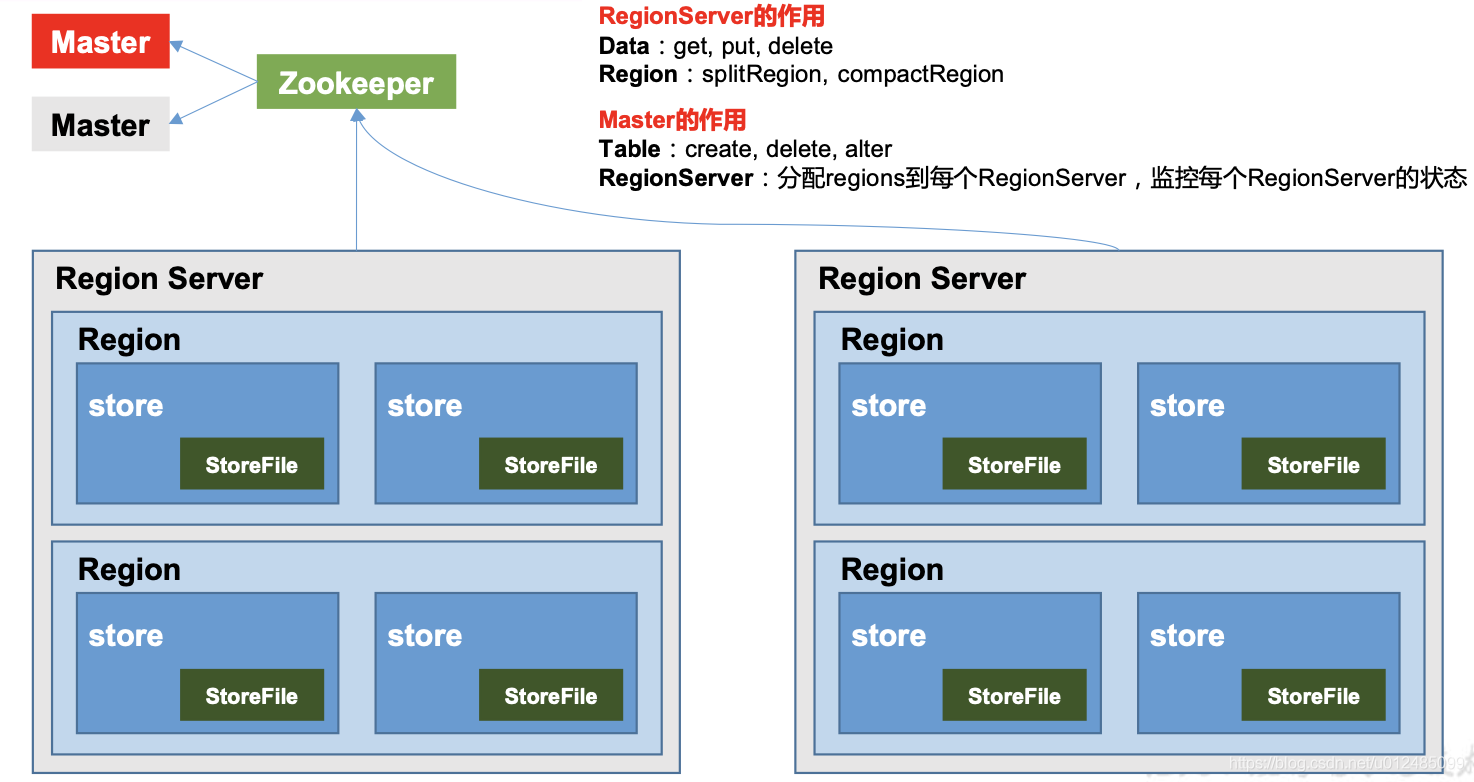
大数据技术之HBase(二)HBase原理简介
一、HBase定义1.1 HBase定义HBase 是一种分布式、可扩展、支持海量数据存储的 NoSQL 数据库非结构化数据存储的数据库,基于列的模式存储。利用Hadoop HDFS作为其文件存储系统,写入性能很强,读取性能较差。利用Hadoop MapReduce来处理HBase中的…...
垒骰子(爆搜/DP)
动态规划方格取数垒骰子方格取数 题目描述 设有 NNN \times NNN 的方格图 (N≤9)(N \le 9)(N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 000。如下图所示(见样例): A0 0 0 0 0 0 0 00 0 13 0 …...

Telink之标准SDK的介绍_1
前提:常见的项目架构:应用层----》驱动层----》硬件层 1、软件组织架构 顶层⽂件夹( 8 个): algorithm,application,boot,common,drivers,proj_lib,stack,v…...

JNI内两种方式从C/C++中传递一维、二维、三维数组数据至Java层详细梳理
目录 0 前言 1 准备工作介绍 2 一维数组 2.1 return形式 2.2 参数形式 3 二维数组 3.1 return形式 3.2 参数形式 4 三维数组 4.1 return形式 4.2 参数形式 5 测试代码 6 结果说明 0 前言 就如之前我写过的一篇文章【JNI内形参从C代码中获取返回值并返回到Java层使…...
)
快递计费系统--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例5:快递计费系统 快递行业高速发展,我们邮寄物品变得方便快捷。某快递点提供华东地区、华南地区、华北地区的寄件服务,其中华东地区编号为01、华南地区编号为02、华北地区编号为03,该快递点寄件价目表具体如表1所示。 表1 寄…...

JS - 自定义一周的开始和结束,计算日期所在月的周数、所在月第几周、所在周的日期范围
自定义一周的开始和结束,计算日期所在月的周数、所在月第几周、所在周的日期范围一. 方法使用二. 实现案例一. 方法使用 根据月开始日期星期几、月结束日期星期几,计算始周、末周占月的天数(每周周期段:上周六 —— 本周五&#x…...

Linux :理解编译的四个阶段
目录一、了解编译二、认识编译的四个阶段(一)预处理(二)编译(三)汇编(四)链接1.静态链接2.动态链接三、分步编译(一)创建.c文件(二)预…...

197.Spark(四):Spark 案例实操,MVC方式代码编程
一、Spark 案例实操 1.数据准备 电商网站的用户行为数据,主要包含用户的 4 种行为:搜索,点击,下单,支付 样例类: 2. Top10 热门品类 先按照点击数排名,靠前的就排名高;如果点击数相同,再比较下单数;下单数再相同,就比较支付数。 我们有多种写法,越往后性能越…...
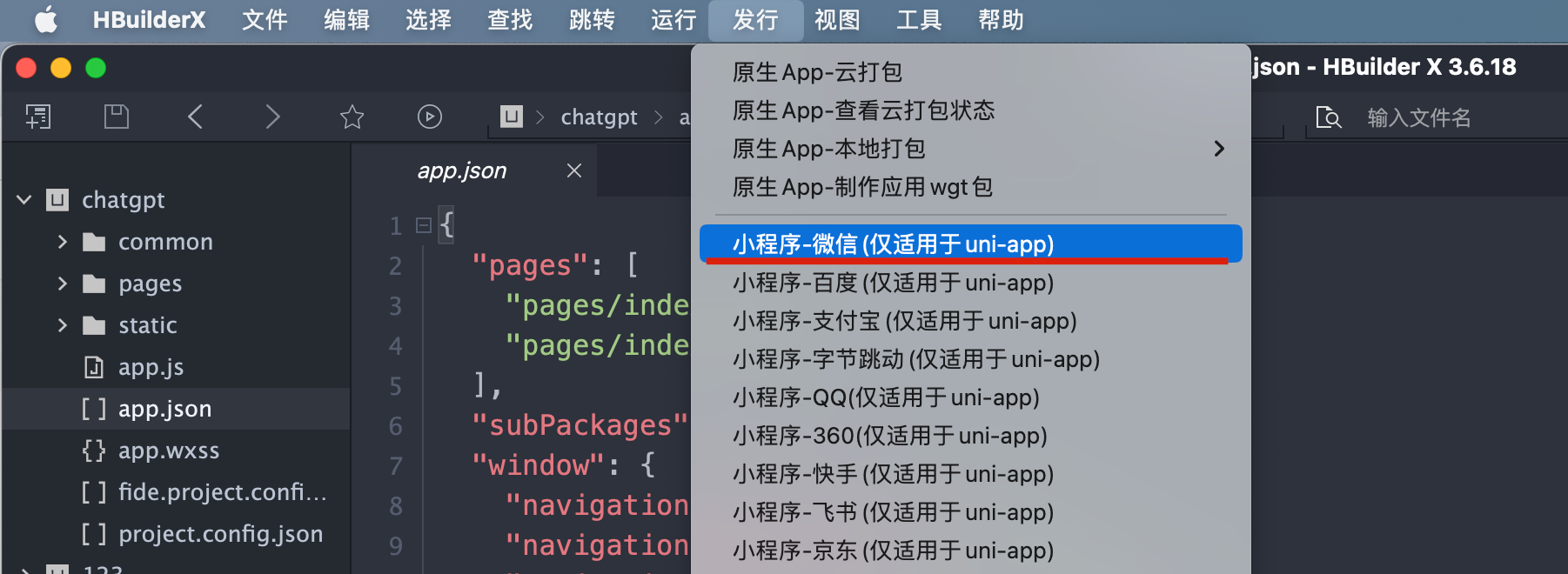
Vue 项目如何迁移小程序
最近我们看到有开发者在社群里提出新的疑惑「我手头已经有一个成熟的 HTML5 项目了,这种项目可以转为小程序在 FinClip 环境中运行吗?」。 经过工作人员的沟通了解,开发者其实是想将已有的 Vue 项目转为小程序,在集成了 FinClip …...

unit1-问候以及介绍
unit1-问候以及介绍 重点表达 1、问好 使用hello 和 hi 来打招呼。hello可以使用在正式和非正式的场合。hi是非正式的。但是hello 和 hi 都可以在一天的任何时段使用。 Hello. 你好。 Hi! 嗨! 介绍你的姓名 使用 I’m 和 My name is 告诉别人你的名字。 I’m Pau…...
杂记——19.git上传时出现the remote end hung up unexpectedly错误
git是大家常用的项目版本控制工具,熟练地使用git可以提高开发效率,但是有时在使用git推送代码时,会提示“the remote end hung up unexpectedly”的问题,那么git推送代码提示“the remote end hung up unexpectedly”怎么解决呢&a…...

python123平台题目
作业二 1. 2的n次方描述输入格式输出格式输入输出实例代码解析2. 输出最大值描述输入格式输出格式输入输出示例代码解析3. 字符串输出描述输入格式输出格式输入输出示例代码解析4. 字符串长度描述输入格式输出格式输入输出示例代码解析...
:TF坐标变换)
ROS学习笔记(六):TF坐标变换
ROS学习笔记(六):TF坐标变换TF的基本知识TF工具tf_monitortf_echostatic_transform_publisherview_frames创建TF广播器创建TF监听器TF的基本知识 TF是一个让用户随时间跟踪多个坐标系的功能包,它使用树形数据结构,根据…...

【python】为你绘制玫瑰一束,爱意永存
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 若是有真情,爱意如溪水, 若是有真爱,爱意如阳光, 若是两情相悦,又岂在朝朝暮暮, 女子淡淡的情愫,深深地想念, 浓浓的爱意&a…...
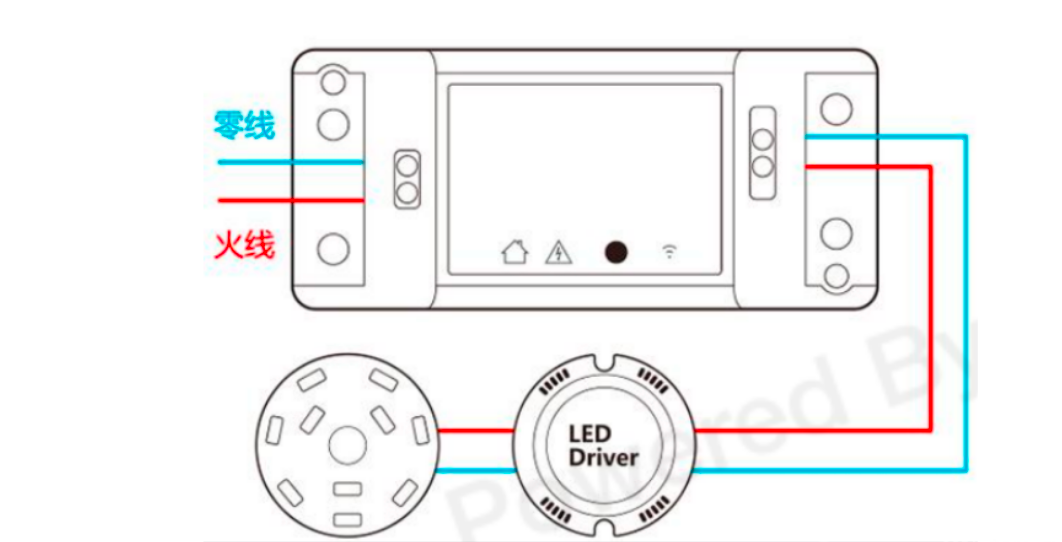
智能家居创意产品一Homkit智能通断器
智能通断器,也叫开关模块,可以非常方便地接入家中原有开关、插座、灯具、电器的线路中,通过手机App或者语音即可控制电路通断,轻松实现原有家居设备的智能化改造。 随着智能家居概念的普及,越来越多的人想将自己的家改…...
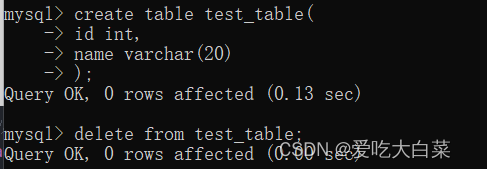
【数据库】MySQL表的增删改查(基础命令详解)
写在前面 : 语法中大写字母是关键字,用[]括这的是可以省略的内容。文中截图是相对应命令执行完得到的结果截图。1.CRUD 注释:在SQL中可以使用“--空格描述”来表示注释说明.CRUD:即增加(Create)、查询(Retrieve)、更新(Update)、删除(Delete)四个单词的首…...

2023年全国最新保安员精选真题及答案15
百分百题库提供保安员考试试题、保安职业资格考试预测题、保安员考试真题、保安职业资格证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 151.该图所要表达的是()消防器材。 A:地上消防栓 B:灭火器 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
