牛客小白月赛90
title: 牛客小白月赛90
date: 2024-04-05 21:37:01
tags: 赛后思考与总结
categories: 比赛
A
思路
按题意直接累加就行
代码
int n; cin >> n;int m; cin >> m;ll ans = 0;vector<int> a(n + 1);for(int i =1; i <= n ; i ++) cin >> a[i];for(int i = 1; i <= m; i ++){int x; cin >> x;ans += a[x];}cout << ans << endl;
B
思路
对双方取余3,如果取余后不相等,则不合法。
代码
int a,b;cin >> a >> b;if(a < b) swap(a,b);a %= 3,b %= 3;if(a == b) cout << "Yes" << endl;else cout << "No" << endl;
C
思路
特判长度为1的数。当个长度大于等于2时,寻找最靠左的非前导0,该位为1,其后面的位置,填1或者0即是最优解,当没有出现0的时候,答案要么是1要么是2。
代码
void solve()
{string s; cin >> s;if(s.size() == 1) cout << 1 << endl;else{int ans = 1;int x = s.size() ;for(int i = 0; i < s.size() ; i ++){if(s[i] == '0') {x = i;break;}}//cout << x << endl;for(int i = x + 1; i < s.size(); i ++){if(s[i] == '0') ans = ans * 10 + 1;else ans *= 10;}if(x == s.size()){if(s[x - 1] == '1') ans = 2;}cout << ans <<endl;}
}
D
思路
因为 m 小于 10,那么情况最多为 2 10 − 1 2 ^ {10} - 1 210−1次,因此二进制枚举每一种情况,当前选还是不选
代码
PII a[N];
void solve()
{int n,m;cin >> n >> m;int ans = 0;vector<int> st(n + 4);for(int i = 0; i < m ; i++){cin >> a[i].x >> a[i].y;}for(int i = 0; i < (1 << m); i ++){for(int j = 0 ; j < m ; j++){if((1 << j) & i){st[a[j].x] ++;st[a[j].y + 1] --;}}int flag = 1;for(int i = 1; i <= n; i ++){st[i] += st[i - 1];if(st[i] < 2) flag = 0;st[i - 1] = 0;}if(flag) ans ++;st[n] = 0;}cout << ans << endl;
}
E
思路
优先队列维护 k 个最小的值。
代码
int a[N],b[N];void solve()
{int n,m;cin >> n >> m;for(int i = 1; i <= n ; i ++) cin >> a[i];for(int i = 1; i <= n ; i ++) cin >> b[i];while(m --){int k ; cin >> k;priority_queue<int> q;ll now = 0;for(int i = 1; i <= k ; i++){q.push(b[i]);now += a[i];now += b[i];}ll res = now;//cout << res <<endl;for(int i = k + 1; i <= n ; i ++){now += a[i];if(b[i] < q.top()){now -= q.top();q.pop();q.push(b[i]);now += b[i];}res = min(res,now);}cout << res << endl;}}
相关文章:

牛客小白月赛90
title: 牛客小白月赛90 date: 2024-04-05 21:37:01 tags: 赛后思考与总结 categories: 比赛 A 思路 按题意直接累加就行 代码 int n; cin >> n;int m; cin >> m;ll ans 0;vector<int> a(n 1);for(int i 1; i < n ; i ) cin >> a[i];for(int i …...
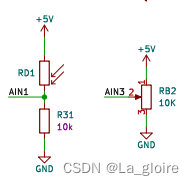
【51单片机入门记录】A/D、D/A转换器PCF859应用
目录 一、IIC初始化代码 二、开发板电路图 三、PCF8591读/写字节操作流程及相关函数 (1)PCF8591(AD)读操作流程及代码 (2)PCF8591(AD)写操作流程及代码 四、应用示例-显示电压…...
:模板方法模式)
设计模式(13):模板方法模式
场景: 实现一个功能时,整体步骤很固定,但是,某些部分易变。易变部分可以抽象出来,供子类实现。 开发中常见的场景 非常繁琐,各个框架,类库中都有它的影子,比如常见的有࿱…...
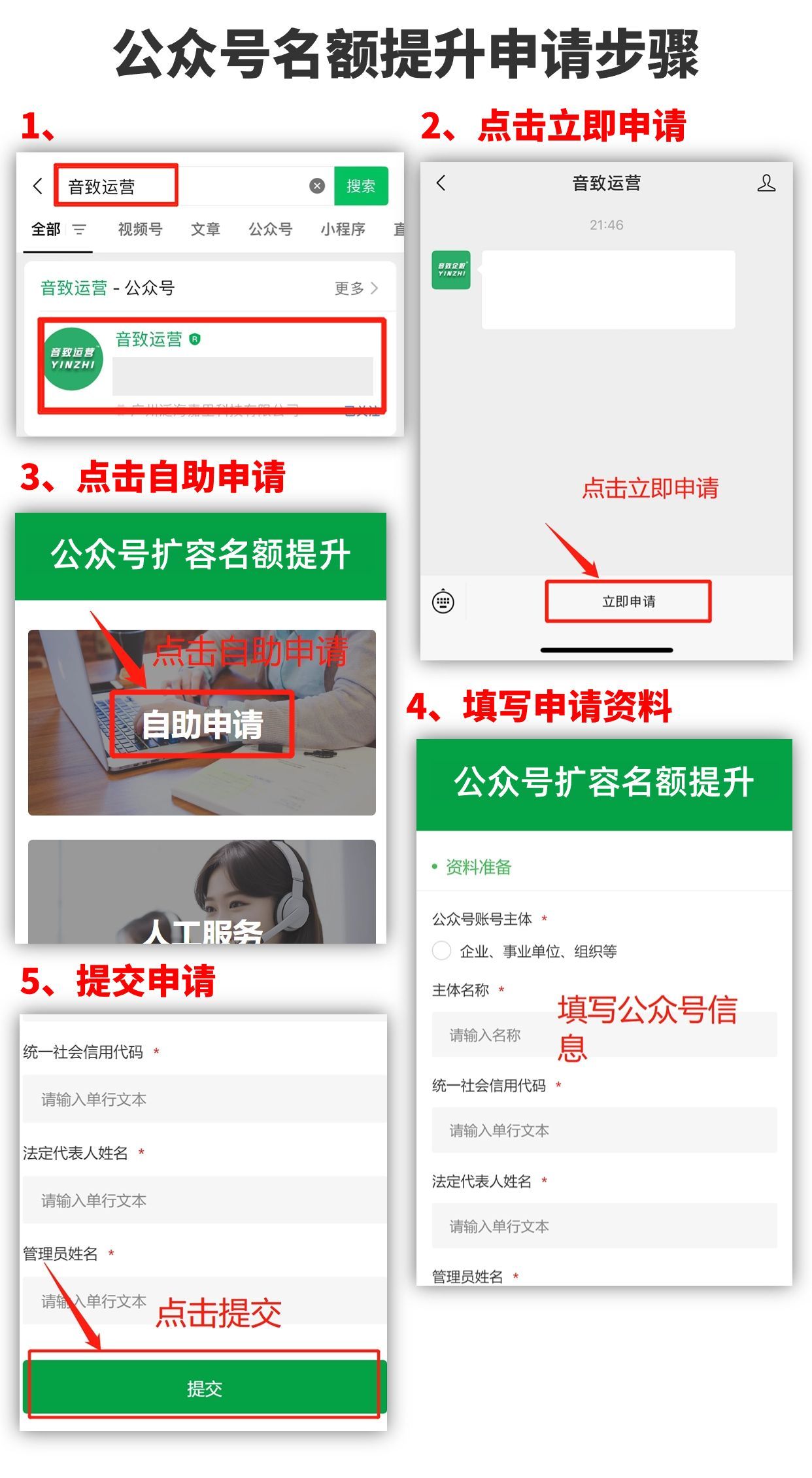
公众号申请上限怎么提升
一般可以申请多少个公众号?众所周知,在2013年前后,公众号申请是不限制数量的,后来企业开始限制申请50个,直到2018年的11月tx又发布,其中个人主体可申请公众号由2个调整为1个,企业主体由50个调整…...

【算法刷题day16】Leetcode:104.二叉树的最大深度 559.n叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数
104.二叉树的最大深度 (优先掌握递归) 文档链接:[代码随想录] 题目链接:104.二叉树的最大深度 (优先掌握递归) 状态:ok 题目: 给定一个二叉树 root ,返回其最大深度。 二…...

电商技术揭秘一:电商架构设计与核心技术
文章目录 引言一、电商平台架构概述1.1 架构设计原则与架构类型选择1.2 传统电商平台架构与现代化架构趋势分析 二、高并发处理与负载均衡2.1 高并发访问特点分析与挑战2.2 负载均衡原理与算法选择 三、分布式数据库与缓存技术3.1 分布式数据库设计与一致性考量3.2 缓存策略与缓…...

Ubuntu 自启动应用程序的方法
1、自启动的方法 自启动应用程序可以在/etc/rc.local文件中调用脚本来启动应用程序,另外也可以自行编写一个服务来启动应用程序。这两种方法其实都是一种方法即使用服务来启动一个应用程序。rc.local脚本本身也是被一个rc.local的服务来调用的。如下图,可…...
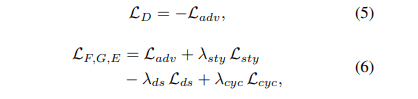
Star GAN论文解析
论文地址:https://arxiv.org/pdf/1912.01865v1.pdf https://openaccess.thecvf.com/content_cvpr_2018/papers/Choi_StarGAN_Unified_Generative_CVPR_2018_paper.pdf 源码:stargan项目实战及源码解读-CSDN博客 1. 概述 在传统方法中&#x…...

全网最强JavaWeb笔记 | 万字长文爆肝JavaWeb开发——day06_数据库-MySQL-02
万字长文爆肝黑马程序员2023最新版JavaWeb教程。这套教程打破常规,不再局限于过时的老套JavaWeb技术,而是与时俱进,运用的都是企业中流行的前沿技术。笔者认真跟着这个教程,再一次认真学习一遍JavaWeb教程,温故而知新&…...
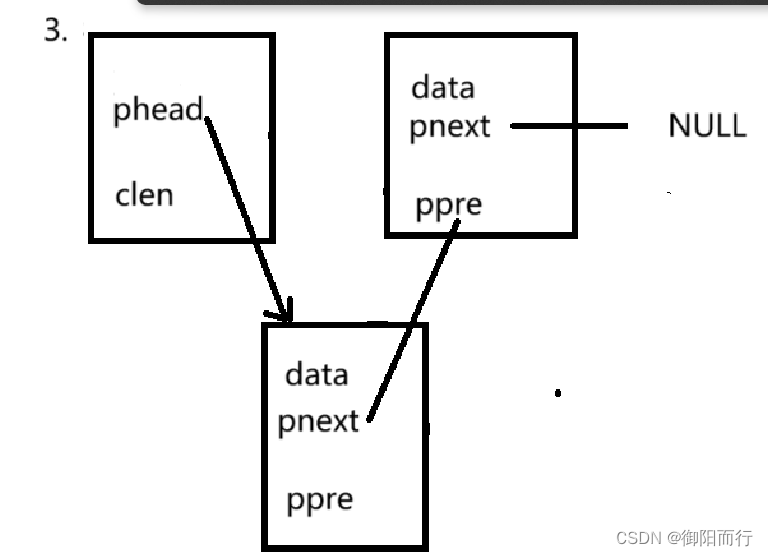
数据结构day2--双向链表
双向链表: 即可以从头遍历到尾部和从尾部遍历到头部的链表,每个结点包括两个链域:前驱指针域和后继指针域,所以比起单向链表,其可以在任意一个结点访问前后两个结点 关于双向链表的一个完整步骤为: 创建一个表头结构…...
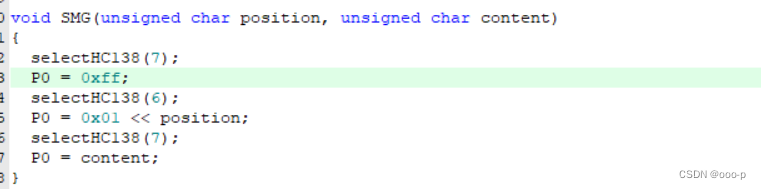
蓝桥杯单片机真题实践篇
这里就不完全写思路过程代码什么的,这一篇文章就写我在训练真题中遇到的过程。 (呜呜呜,时间不够辣,能做多少算多少吧....) 十三届省赛题 问题1:数码管的数字消影不明显 (参考:蓝…...

前端pdf.js将pdf转为图片,尤其适合电子发票打印
写这个的原因就是打电子发票不方便,这个代码是纯js不需要后端服务直接将两张电子发票的pdf转为两张图片渲染到一张A4纸上面(完全不浪费,发票也不会变大),自动完成打印分页,点击打印即可。亲测可用所有电子发…...

第四百四十三回
文章目录 1. 概念介绍2. 思路与方法2.1 整体思路2.2 使用方法 3. 示例代码4. 内容总结 我们在上一章回中介绍了"自定义Action菜单"相关的内容,本章回中将介绍如何获取屏幕相关参数.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本…...

一分钟快速用上号称“音乐版ChatGPT”的suno AI,适合普通人的超简单教程!
随着AI的应用变广,各类AI程序已逐渐普及。AI已逐渐深入到人们的工作生活方方面面。而AI涉及的行业也越来越多,从最初的写作,到医疗教育,再到现在的音乐。 Suno是一个专业高质量的AI歌曲和音乐创作平台,用户只需输入简…...
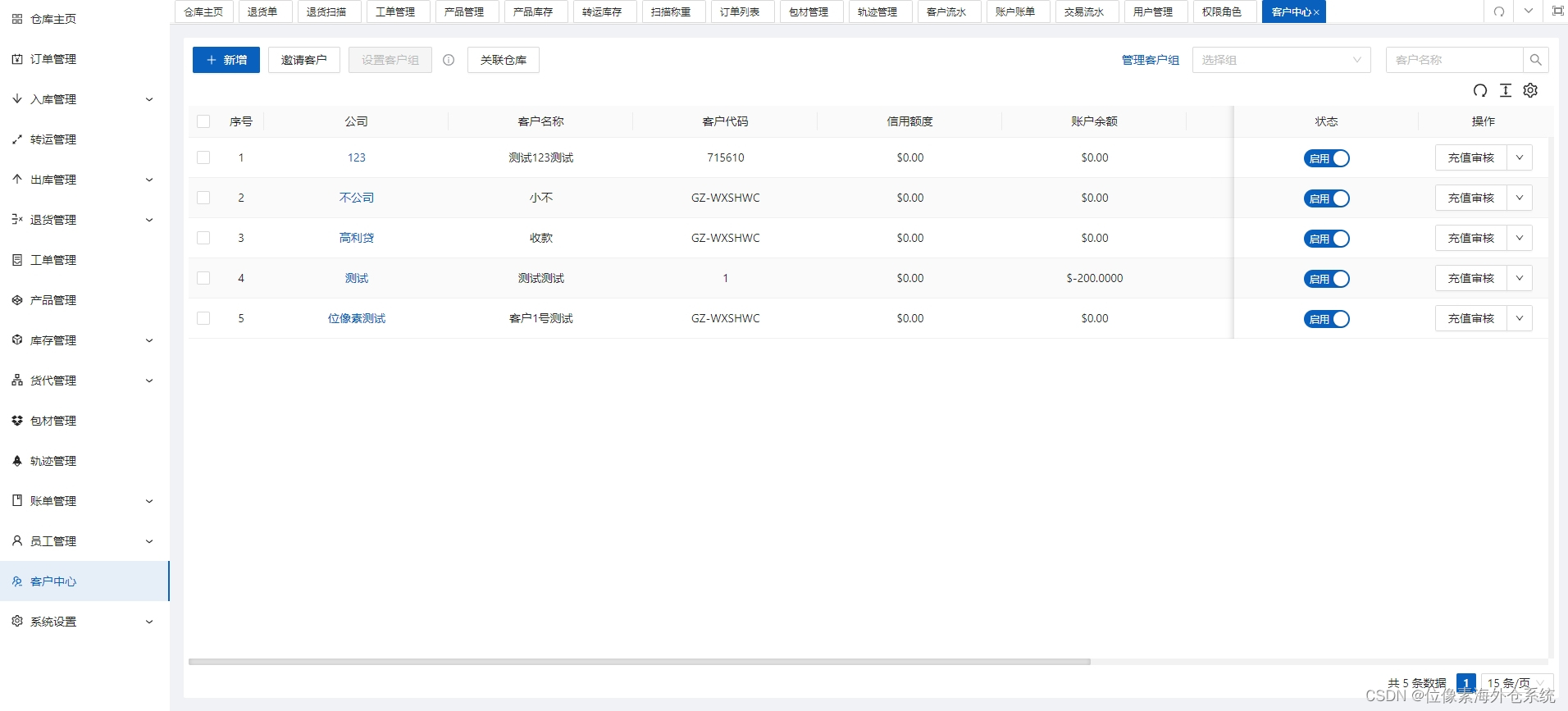
干货!一文读懂:位像素海外仓系统的分销功能
随着跨境电商的蓬勃发展,海外仓系统的重要性日益凸显,成为企业在激烈市场竞争中脱颖而出的关键。当谈及海外仓系统的拓展功能,特别是其中的分销功能,正逐渐成为卖家们不可或缺的工具。 那么,这个神奇的分销功能究竟是…...

【洛谷】P1449 后缀表达式
题目描述 所谓后缀表达式是指这样的一个表达式:式中不再引用括号,运算符号放在两个运算对象之后,所有计算按运算符号出现的顺序,严格地由左而右新进行(不用考虑运算符的优先级)。 本题中运算符仅包含 -*…...

【MySQL】聚合函数和分组聚合
👦个人主页:Weraphael ✍🏻作者简介:目前学习计网、mysql和算法 ✈️专栏:MySQL学习 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬…...
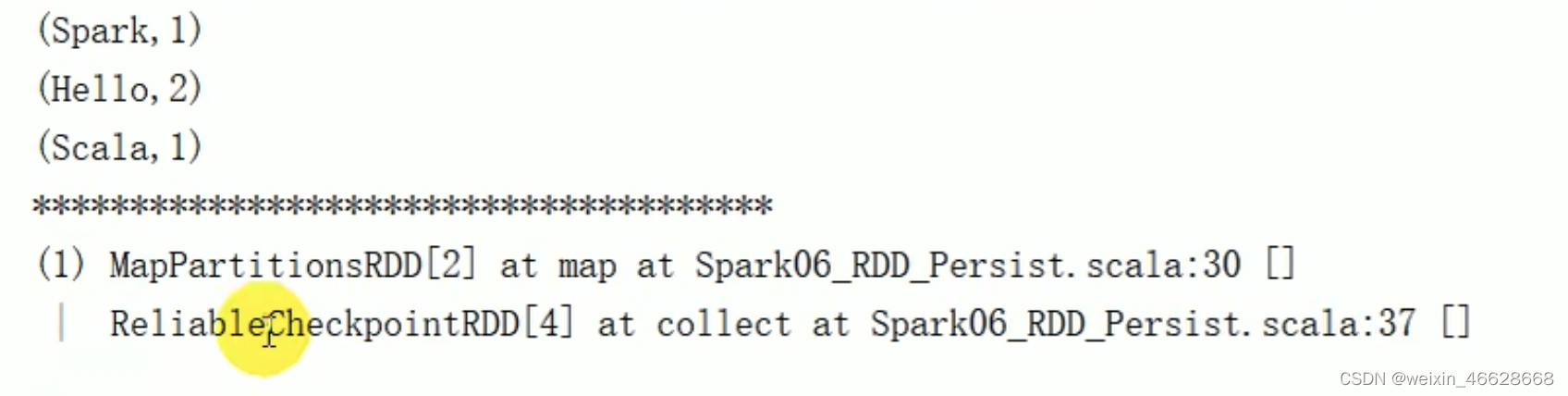
RDD算子(四)、血缘关系、持久化
1. foreach 分布式遍历每一个元素,调用指定函数 val rdd sc.makeRDD(List(1, 2, 3, 4)) rdd.foreach(println) 结果是随机的,因为foreach是在每一个Executor端并发执行,所以顺序是不确定的。如果采集collect之后再调用foreach打印…...
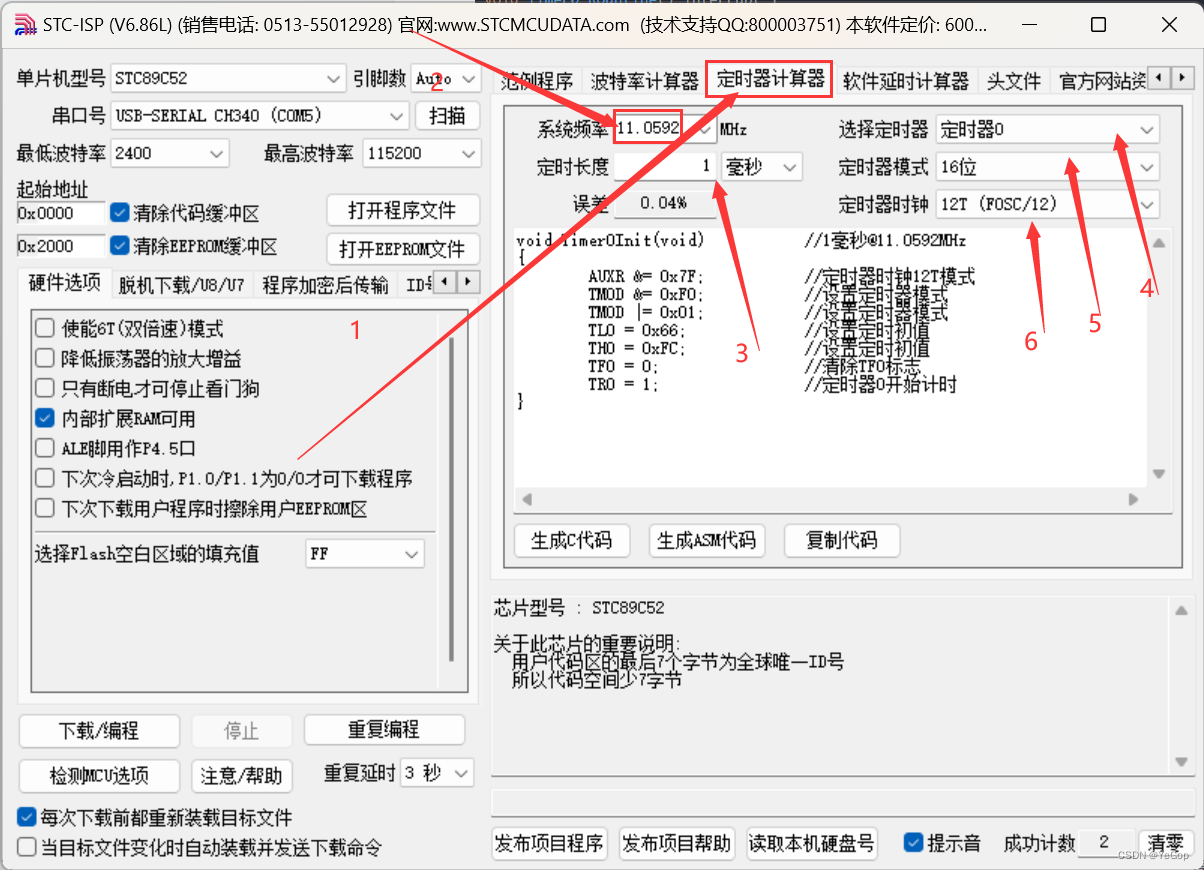
51之定时器与中断系统
目录 1.定时器与中断系统简介 1.1中断系统 1.2定时器 1.2.1定时器简介 1.2.2定时器大致原理及其配置 1.2.3定时器所需的所有配置总介 2.定时器0实现LED闪烁 3.使用软件生成定时器初始化程序 1.定时器与中断系统简介 1.1中断系统 首先,我们需要来了解一下什么…...

C语言中的内存函数
相比于内存函数,字符串函数和字符函数是对字符串和字符进行操作,内存函数是对内存进行操的。下面跟大家分享我学到的几个内存函数。 memcpy函数 void* memcpy(void* dest, const void* sour, size_t num); dest是目标地址,sour要拷贝的源地…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
