蓝桥杯第十四届C++A组(未完)
【规律题】平方差
题目描述
给定 L, R,问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 。
输入格式
输入一行包含两个整数 L, R,用一个空格分隔。
输出格式
输出一行包含一个整数满足题目给定条件的 x 的数量。
样例输入
1 5
样例输出
4
提示
对于 40% 的评测用例,LR ≤ 5000 ;
对于所有评测用例,1 ≤ L ≤ R ≤ 10^9 。
由得
,
令 ,则
,解得:
要使y和z有整数解,那么 为偶数,
(1)偶数+偶数=偶数,偶数-偶数=偶数;
(2)奇数+奇数=偶数,奇数-奇数=偶数;
则m和n奇偶性相同,即如果x有一对因子奇偶性相同,那么一定可以找到y,z满足。
(1)若m,n都为偶数,那么m是2的倍数,n是2的倍数,那么m*n一定是4的倍数。
(2)若m,n都为奇数,那么由性质 奇数*奇数=奇数 得,m*n也一定为奇数。
综上 x 是四的倍数或者奇数。
#include<iostream>
#include<cstring>
#include<map>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
const int N=10010;
int main(){LL L,R;cin>>L>>R;int cnt=0;for(LL i=L;i<=R;i++){if(i%4==0||i%2){cnt++;}}cout<<cnt<<endl;return 0;
}更小的数
题目描述
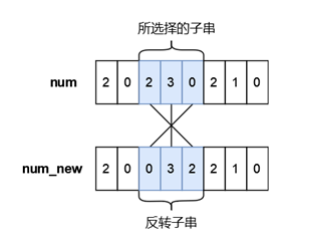
小蓝有一个长度均为 n 且仅由数字字符 0 ∼ 9 组成的字符串,下标从 0 到 n − 1,你可以将其视作是一个具有 n 位的十进制数字 num,小蓝可以从 num 中选出一段连续的子串并将子串进行反转,最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 numnew 满足条件 numnew < num,请你帮他计算下一共有多少种不同的子串选择方案,只要两个子串在 num 中的位置不完全相同我们就视作是不同的方案。
注意,我们允许前导零的存在,即数字的最高位可以是 0 ,这是合法的。
输入格式
输入一行包含一个长度为 n 的字符串表示 num(仅包含数字字符 0 ∼ 9),
从左至右下标依次为 0 ∼ n − 1。
输出格式
输出一行包含一个整数表示答案。
样例输入
210102
样例输出
8
提示
一共有 8 种不同的方案:
1)所选择的子串下标为 0 ∼ 1 ,反转后的 numnew = 120102 < 210102 ;
2)所选择的子串下标为 0 ∼ 2 ,反转后的 numnew = 012102 < 210102 ;
3)所选择的子串下标为 0 ∼ 3 ,反转后的 numnew = 101202 < 210102 ;
4)所选择的子串下标为 0 ∼ 4 ,反转后的 numnew = 010122 < 210102 ;
5)所选择的子串下标为 0 ∼ 5 ,反转后的 numnew = 201012 < 210102 ;
6)所选择的子串下标为 1 ∼ 2 ,反转后的 numnew = 201102 < 210102 ;
7)所选择的子串下标为 1 ∼ 4 ,反转后的 numnew = 201012 < 210102 ;
8)所选择的子串下标为 3 ∼ 4 ,反转后的 numnew = 210012 < 210102 ;
对于 20% 的评测用例,1 ≤ n ≤ 100 ;
对于 40% 的评测用例,1 ≤ n ≤ 1000 ;
对于所有评测用例,1 ≤ n ≤ 5000 。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
int main(){string s;cin>>s;int n=s.size();int cnt=0;for(int i=0;i<n-1;i++){for(int j=n-1;j>i;j--){if(s[i]>s[j]) cnt++;else if(s[i]==s[j]){for(int x=i,y=j;x<y;x++,y--){if(s[x]>s[y]){cnt++;break;}else if(s[x]<s[y]) break;}}}}cout<<cnt<<endl;return 0;
}【DFS】颜色平衡树
题目描述
给定一棵树,结点由 1 至 n 编号,其中结点 1 是树根。树的每个点有一个颜色 Ci。
如果一棵树中存在的每种颜色的结点个数都相同,则我们称它是一棵颜色平衡树。
求出这棵树中有多少个子树是颜色平衡树。
输入格式
输入的第一行包含一个整数 n ,表示树的结点数。
接下来 n 行,每行包含两个整数 Ci , Fi,用一个空格分隔,表示第 i 个结点的颜色和父亲结点编号。
特别地,输入数据保证 F1 为 0 ,也即 1 号点没有父亲结点。保证输入数据是一棵树。
输出格式
输出一行包含一个整数表示答案。
样例输入
6 2 0 2 1 1 2 3 3 3 4 1 4
样例输出
4
提示
编号为 1, 3, 5, 6 的 4 个结点对应的子树为颜色平衡树。
对于 30% 的评测用例,n ≤ 200,Ci ≤ 200 ;
对于 60% 的评测用例,n ≤ 5000,Ci ≤ 5000 ;
对于所有评测用例,1 ≤ n ≤ 200000,1 ≤ Ci ≤ 200000,0 ≤ Fi < i 。
#include<iostream>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
const int N=2e5+10;
int c[N];
int ans=0;
int n;
vector<int> g[N];
void add(map<int,int> &cnt,map<int,int> &cnt_nb){for(auto mp:cnt_nb){int x=mp.first;int y=mp.second;cnt[x]+=y;}
}
map<int,int> dfs(vector<int> *g,int *c,int i){int sz=g[i].size();map<int,int> cnt;if(sz==0){cnt[c[i]]=1;ans++;return cnt;}cnt[c[i]]=1;for(int j=0;j<sz;j++){int nb=g[i][j];map<int,int> cnt_nb=dfs(g,c,nb);add(cnt,cnt_nb);}int num=cnt[c[i]];for(auto mp:cnt){int count=mp.second;if(count!=num) return cnt;}ans++;return cnt;
}
int main(){cin>>n;for(int i=0;i<n;i++){int f;cin>>c[i]>>f;if(f>=1) g[f-1].push_back(i);}dfs(g,c,0);cout<<ans<<endl;return 0;
}【DFS】(选不选)买瓜
题目描述
小蓝正在一个瓜摊上买瓜。瓜摊上共有 n 个瓜,每个瓜的重量为 Ai 。
小蓝刀功了得,他可以把任何瓜劈成完全等重的两份,不过每个瓜只能劈一刀。
小蓝希望买到的瓜的重量的和恰好为 m 。
请问小蓝至少要劈多少个瓜才能买到重量恰好为 m 的瓜。如果无论怎样小蓝都无法得到总重恰好为 m 的瓜,请输出 −1 。
输入格式
输入的第一行包含两个整数 n, m,用一个空格分隔,分别表示瓜的个数和小蓝想买到的瓜的总重量。
第二行包含 n 个整数 Ai,相邻整数之间使用一个空格分隔,分别表示每个瓜的重量。
输出格式
输出一行包含一个整数表示答案。
样例输入
3 10 1 3 13
样例输出
2
提示
对于 20% 的评测用例,∑n≤10;
对于 60% 的评测用例,∑n≤20;
对于所有评测用例,1 ≤n≤30,1≤ Ai ≤ 10^9 ,1 ≤ m ≤ 10^9
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N=35,INF=0x3f3f3f3f;
LL p[N];
LL a[N];
int n;
LL m;
int ans=INF;
void dfs(int u,LL sum,int cnt){if(sum==m){ans=min(ans,cnt);return ;}if(cnt>=ans||u>n||sum+p[u]<m||sum>m) return ;dfs(u+1,sum+a[u],cnt);dfs(u+1,sum+a[u]/2,cnt+1);dfs(u+1,sum,cnt);
}
int main(){cin>>n>>m;m*=2;for(int i=1;i<=n;i++){cin>>a[i];a[i]*=2;}sort(a+1,a+1+n,greater<int>());for(int i=n;i>=1;i--) p[i]=p[i+1]+a[i];dfs(1,0,0);if(ans==INF) cout<<"-1"<<endl;else cout<<ans<<endl;return 0;
}网络稳定性(X)
异或和之和
题目描述
给定一个数组 Ai,分别求其每个子段的异或和,并求出它们的和。或者说,对于每组满足 1 ≤ L ≤ R ≤ n 的 L, R ,求出数组中第 L 至第 R 个元素的异或和。然后输出每组 L, R 得到的结果加起来的值。
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数 Ai ,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
5 1 2 3 4 5
样例输出
39
提示
对于 30% 的评测用例,n ≤ 300 ;
对于 60% 的评测用例,n ≤ 5000 ;
对于所有评测用例,1 ≤ n ≤ 105,0 ≤ Ai ≤ 2^20 。
区间[l,r]的异或和可以表示为,这样原问题就变成了:求n+1个数两两异或之和,如果
的二进制第 j 位为1(0),我们只需知道 [0,i-1] 这个区间内的数二进制第 j 位为0(1)的个数x,这样s[i]的第 j 位的贡献值为x*2^j;
#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N][30];
signed main(){int n;cin>>n;int x;for(int i=1;i<=n;i++){cin>>x;for(int j=0;j<=20;j++){a[i][j]=(x>>j)&1;a[i][j]^=a[i-1][j];}}int ans=0;for(int j=0;j<=20;j++){map<int,int> mp;mp[0]++;for(int i=1;i<=n;i++){int x=mp[a[i][j]^1];//与第i个数第j位不同的个数ans+=(1<<j)*x;mp[a[i][j]]++;}}cout<<ans<<endl;return 0;
}#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
int s[N];
int cnt[N][30];
signed main(){int n;cin>>n;int x;for(int i=1;i<=n;i++){cin>>a[i];s[i]=s[i-1]^a[i];}
//求n+1个数第j位0和1的个数for(int j=0;j<=20;j++){for(int i=0;i<=n;i++){if(s[i]>>j&1) cnt[j][1]++;else cnt[j][0]++;}}int ans=0;for(int i=0;i<=20;i++){
//每个1都可以和每个0异或等于1,总数为cnt[i][0]*cnt[i][1],每个1的贡献值为2^ians+=cnt[i][0]*cnt[i][1]*(1<<i);}cout<<ans<<endl;return 0;
}像素放置(X)
翻转硬币(X)
相关文章:
蓝桥杯第十四届C++A组(未完)
【规律题】平方差 题目描述 给定 L, R,问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 。 输入格式 输入一行包含两个整数 L, R,用一个空格分隔。 输出格式 输出一行包含一个整数满足题目给定条件的 x 的数量。 样例输入 1 5 样例输出 …...

职场口才提升之道
职场口才提升之道 在职场中,口才的重要性不言而喻。无论是与同事沟通协作,还是向上级汇报工作,亦或是与客户洽谈业务,都需要具备良好的口才能力。一个出色的职场人,除了拥有扎实的专业技能外,还应具备出色…...
【算法练习】28:选择排序学习笔记
一、选择排序的算法思想 弄懂选择排序算法,先得知道两个概念:未排序序列,已排序序列。 原理:以升序为例,选择排序算法的思想是,先将整个序列当做未排序的序列,以序列的第一个元素开始。然后从左…...
【关于窗口移动求和的两种计算方法】
窗口移动计算方法 例子方法1方法2运行结果: 例子 在很多算法中都会涉及到窗口滑动,比如基于新息序列更新的自适应卡尔曼滤波器算法中便会使用到。 已知一个数列:OCV [1;2;3;4;5;6;7;8;9;10;11;12;13;14;15],定义窗口长度为5,每次…...

Win10文件夹共享(有密码的安全共享)(SMB协议共享)
前言 局域网内(无安全问题,比如自己家里wifi)无密码访问,参考之前的操作视频 【电脑文件全平台共享、播放器推荐】手机、电视、平板播放硬盘中的音、视频资源 下面讲解公共网络如办公室网络、咖啡厅网络等等环境下带密码的安全…...

Client sent an HTTP request to an HTTPS server
背景 最近踩坑了 我发现域名:8000可以访问我的服务 但是域名:443却不行,这很反常 结果发现是nginx配置的问题,需要把http改成https! 原因 如果你的后端服务(运行在8000端口上)已经配置了SS…...

Springboot传参要求
Web.java(这里定义了一个实体类交Web) public class Web{ private int Page; public int getPage() {return Page;}public void setPage(int page) {Page page;} } 1、通过编译器自带的getter、Setter传参 。只是要注意参数的名字是固定的,不能灵活改变。 传参的…...

数字乡村创新实践探索:科技赋能农业现代化与乡村治理体系现代化同步推进
随着信息技术的飞速发展,数字乡村作为乡村振兴的重要战略方向,正日益成为推动农业现代化和乡村治理体系现代化的关键力量。科技赋能下的数字乡村,不仅提高了农业生产的效率和品质,也为乡村治理带来了新的机遇和挑战。本文旨在探讨…...

C语言——找单身狗1
题目描述: 在一个整形数组中,只有一个数字出现一次,其他数组都是成对出现的,找出那个只出现一次的数字。 例如: 数组中:1,2,3,4,5,4,3…...

Day82:服务攻防-开发组件安全Solr搜索Shiro身份Log4j日志本地CVE环境复现
目录 J2EE-组件Solr-本地demo&CVE 命令执行(CVE-2019-17558) 远程命令执行漏洞(CVE-2019-0193) Apache Solr 文件读取&SSRF (CVE-2021-27905) J2EE-组件Shiro-本地demo&CVE CVE_2016_4437 Shiro-550Shiro-721(RCE) CVE-2020-11989(身…...
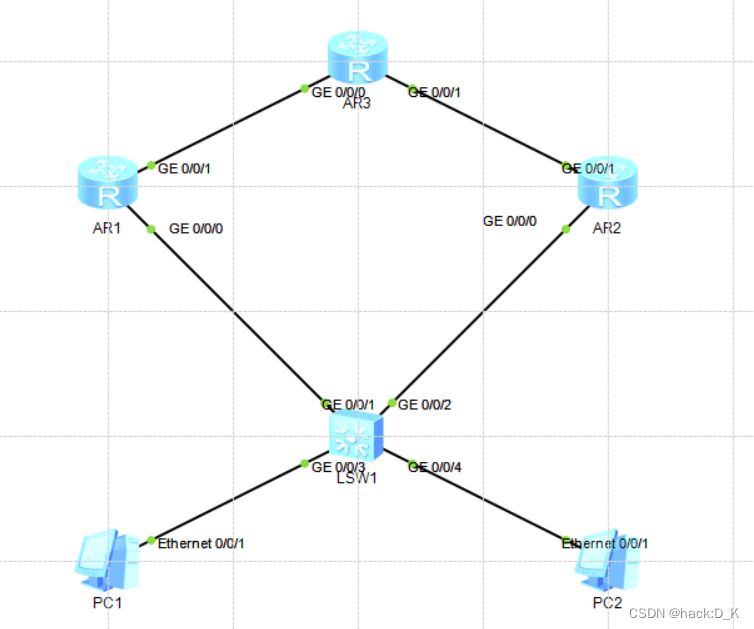
网络协议——VRRP(虚拟路由冗余协议)原理与配置
1. VRRP概述 单网关出现故障后下联业务中断,配置两个及以上的网关时由于IP地址冲突,导致通讯时断时续甚至通信中断。VRRP组播类的网络层协议 2. 协议版本 VRRP v2: 支持认证,仅适用于IPv4网络 VRRP v3: 不支持认证, 适用于IPv4和IPv6两种网…...
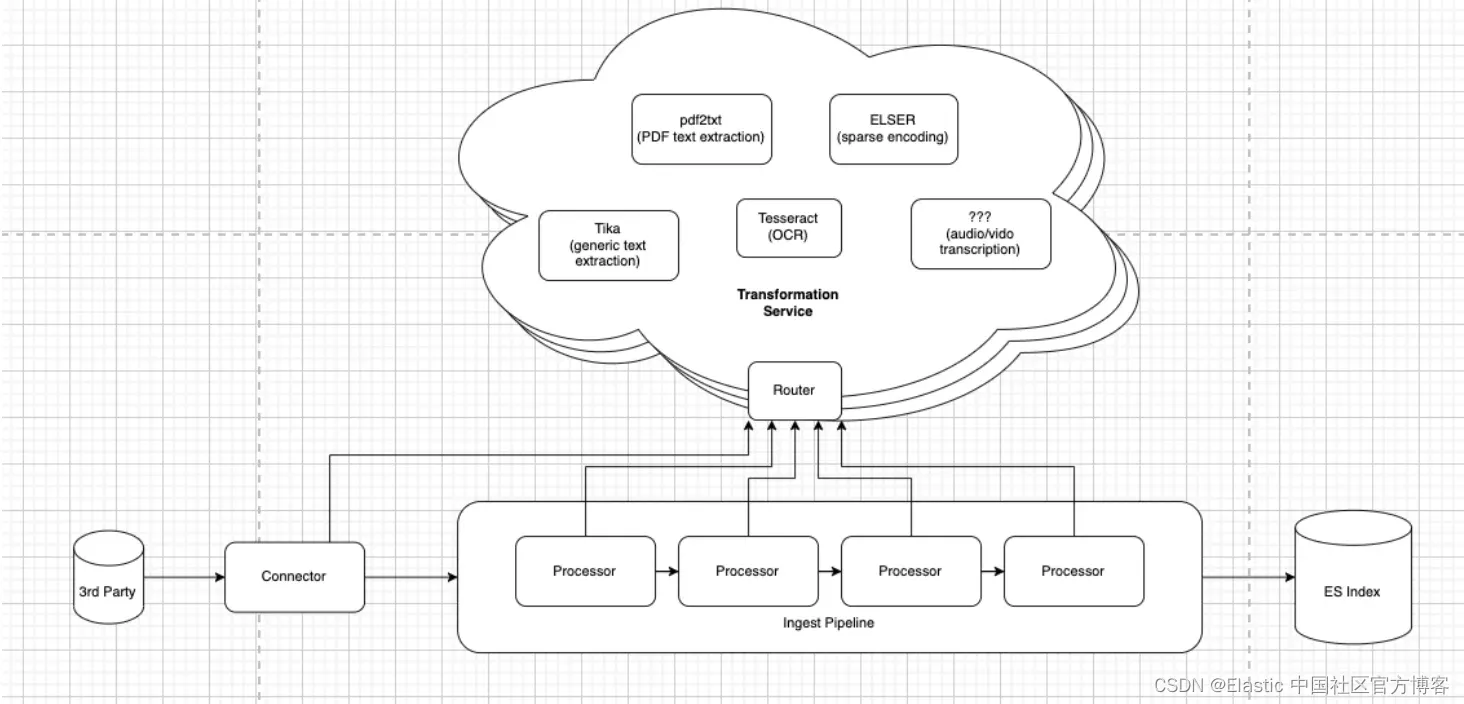
Elasticsearch:我们如何演化处理二进制文档格式
作者:来自 Elastic Sean Story 从二进制文件中提取内容是一个常见的用例。一些 PDF 文件可能非常庞大 — 考虑到几 GB 甚至更多。Elastic 在处理此类文档方面已经取得了长足的进步,今天,我们很高兴地介绍我们的新工具 —— 数据提取服务&…...
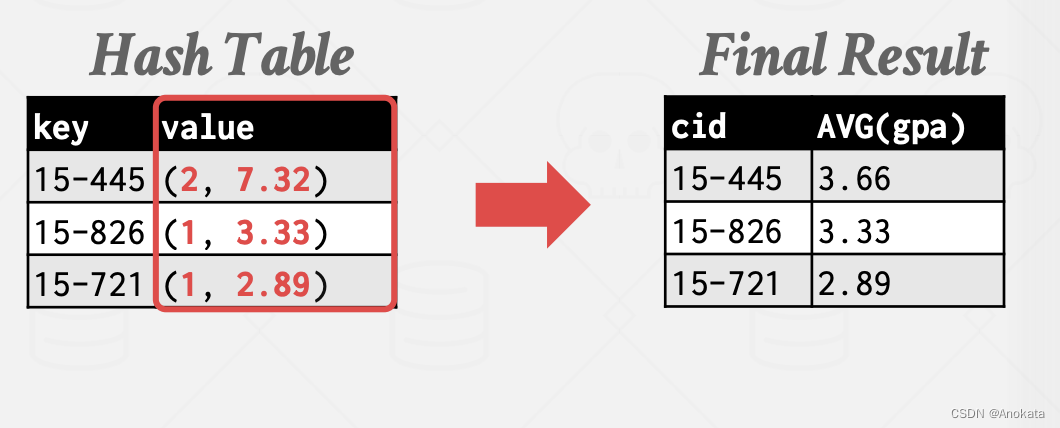
第八讲 Sort Aggregate 算法
我们现在将讨论如何使用迄今为止讨论过的 DBMS 组件来执行查询。 1 查询计划【Query Plan】 我们首先来看当一个查询【Query】被解析【Parsed】后会发生什么? 当 SQL 查询被提供给数据库执行引擎,它将通过语法解析器进行检查,然后它会被转换…...
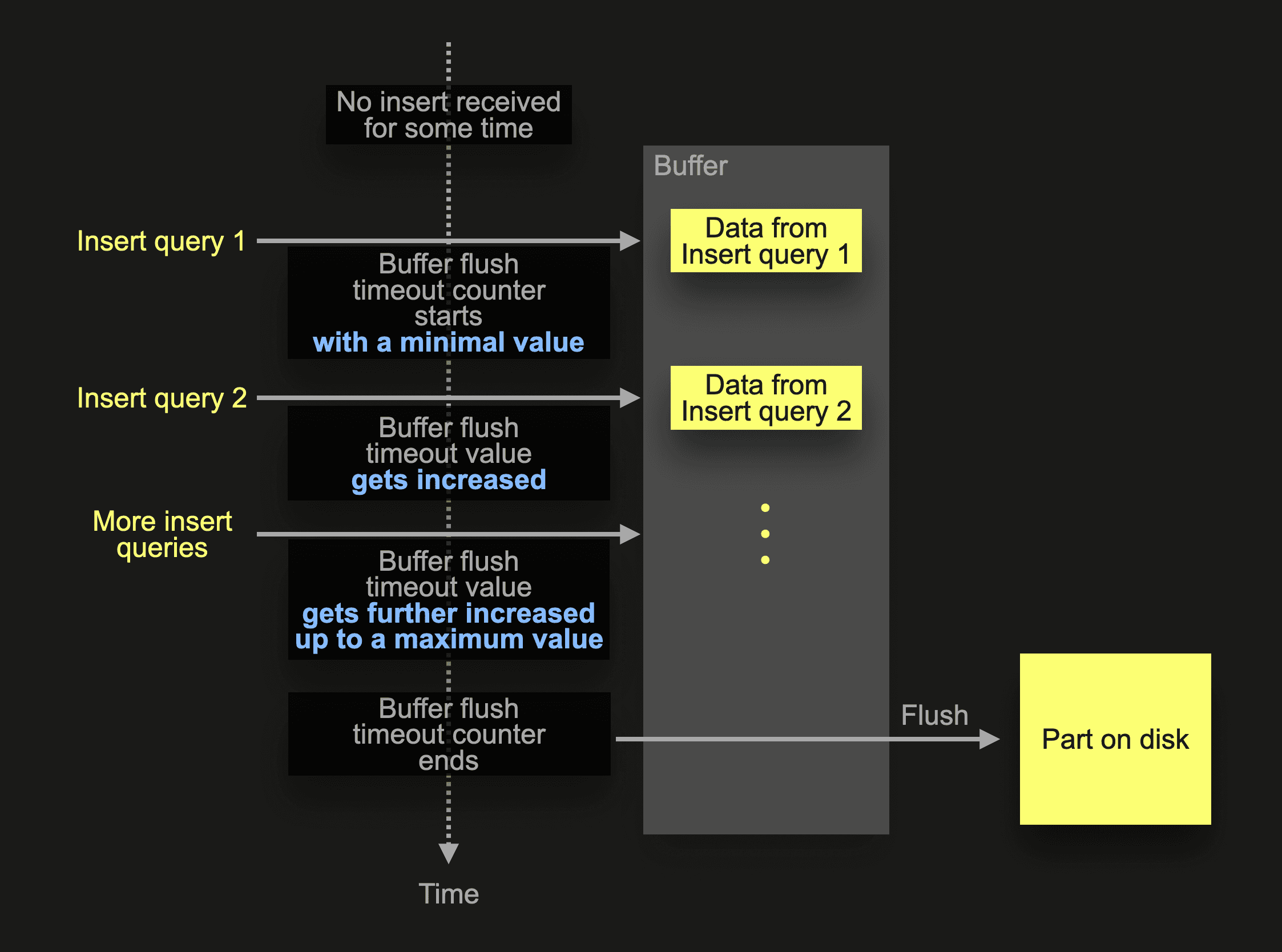
clickhouse MPPDB数据库--新特性使用示例
clickhouse 新特性: 从clickhouse 22.3至最新的版本24.3.2.23,clickhouse在快速发展中,每个版本都增加了一些新的特性,在数据写入、查询方面都有性能加速。 本文根据clickhouse blog中的clickhouse release blog中,学…...
MATLAB多级分组绘图及图例等细节处理 ; MATLAB画图横轴时间纵轴数值按照不同sensorCode分组画不同sensorCode的曲线
平时研究需要大量的绘图Excel有时候又臃肿且麻烦 尤其是当处理大量数据时可能会拖死Windows 示例代码及数据量展示 因为数据量是万级别的折线图也变成"柱状图"了, 不过还能看出大致趋势! 横轴是时间纵轴是传感器数值图例是传感器所在深度 % data readtable(C:\U…...

20240405,数据类型,运算符,程序流程结构
是我深夜爆炸,不能再去补救C了,真的来不及了,不能再三天打鱼两天晒网了,真的来不及了呜呜呜呜 我实在是不知道看什么课,那黑马吧……MOOC的北邮的C正在进行呜呜 #include <iostream> using namespace std; int…...
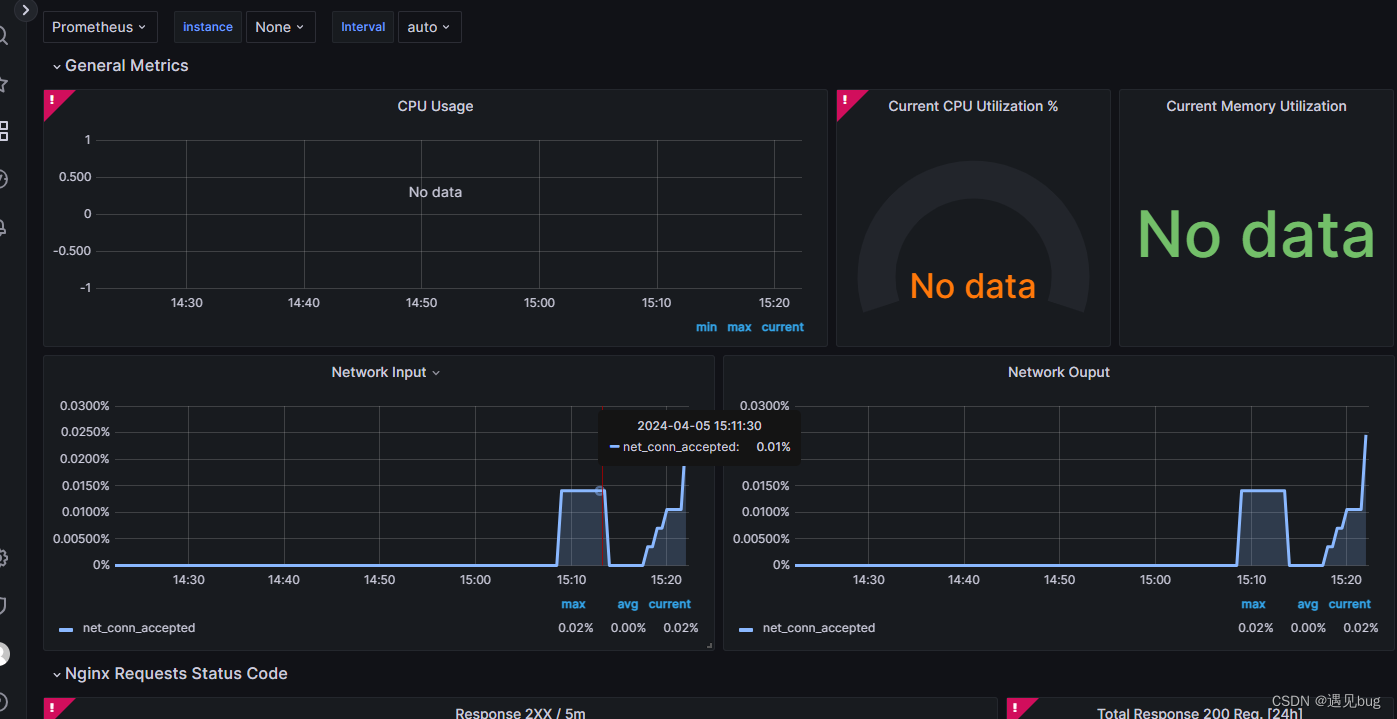
Prometheus+grafana环境搭建Nginx(docker+二进制两种方式安装)(六)
由于所有组件写一篇幅过长,所以每个组件分一篇方便查看,前五篇链接如下 Prometheusgrafana环境搭建方法及流程两种方式(docker和源码包)(一)-CSDN博客 Prometheusgrafana环境搭建rabbitmq(docker二进制两种方式安装)(二)-CSDN博客 Prometheusgrafana环…...

贝叶斯逻辑回归
贝叶斯逻辑回归(Bayesian Logistic Regression)是一种机器学习算法,用于解决分类问题。它基于贝叶斯定理,通过建立一个逻辑回归模型,结合先验概率和后验概率,对数据进行分类。 贝叶斯逻辑回归的基本原理是…...

Win10 下 Vision Mamba(Vim-main)的环境配置(libcuda.so文件无法找到,windows系统运行失败)
目录 1、下载NVIDIA 驱动程序、cuda11.8、cudnn8.6.0 2、在Anaconda中创建环境并激活 3、下载gpu版本的torch 4、配置环境所需要的包 5、安装causal_conv1d和mamba-1p1p1 安装causal_conv1d 安装mamba-1p1p1 6、运行main.py失败 请直接拉到最后查看运行失败的原因&am…...

4 万字全面掌握数据库、数据仓库、数据集市、数据湖、数据中台
如今,随着诸如互联网以及物联网等技术的不断发展,越来越多的数据被生产出来-据统计,每天大约有超过2.5亿亿字节的各种各样数据产生。这些数据需要被存储起来并且能够被方便的分析和利用。 随着大数据技术的不断更新和迭代,数据管…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
