java数据结构与算法刷题-----LeetCode172. 阶乘后的零
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
文章目录
- 数学:阶乘的10因子个数
- 数学优化:思路转变为求5的倍数的个数
数学:阶乘的10因子个数
| 解题思路:时间复杂度O( n n n),n为5的个数,空间复杂度O( 1 1 1) |
|---|
- 如果想要求出阶乘,一定会超时。所以我们要找到破题点。就是什么条件下阶乘末尾会出现0。
- 我们发现阶乘结果求出来后,不断的提出因子10,能提出多少次,就有几个0. 例如5!=120. 此时进行因式分解为: 10 ∗ ( 12 ) . 10*(12). 10∗(12).一共提出1个10,因此一共一个0.
- 10是由2和5构成的。而且5的个数绝对更少。例如120 = 5 ∗ ( 24 ) 5*(24) 5∗(24) = 2 ∗ 2 ∗ 2 ∗ ( 15 ) 2*2*2*(15) 2∗2∗2∗(15).我们发现5的个数决定了阶乘结果中可以和2组成几个10.
- 因此我们可以先尝试统计n的阶乘中,5的个数。试一下效果
我们不需要每个阶乘数字都统计,例如5!中只有5这个数会出现5.因为5!=1*2*3*4*5.明眼人都知道,1,2,3,4不会有5的出现。
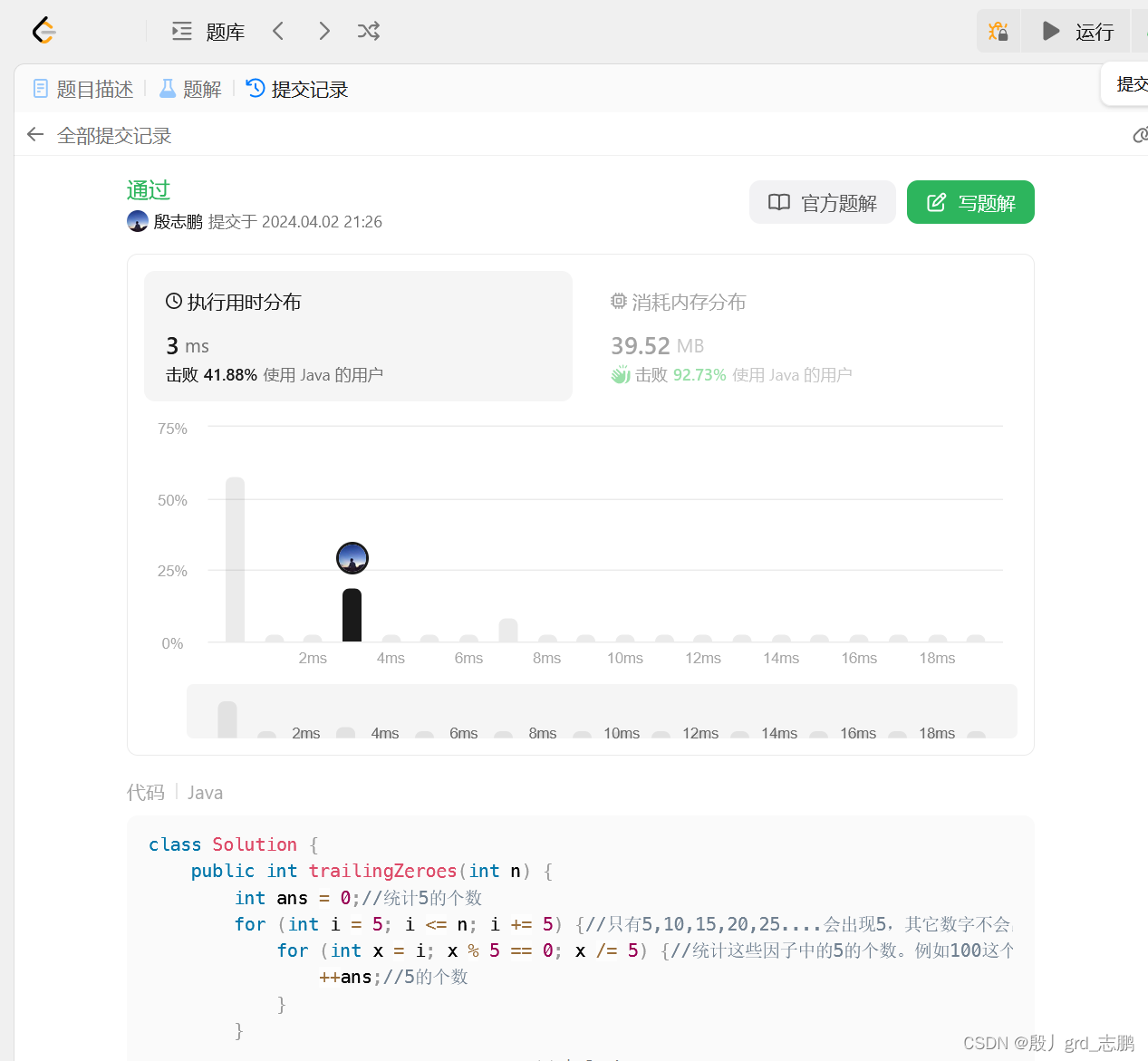
| 代码:最起码通过了对吗,说明想法没错,接下来法二会继续优化 |
|---|
class Solution {public int trailingZeroes(int n) {int ans = 0;//统计5的个数for (int i = 5; i <= n; i += 5) {//只有5,10,15,20,25....会出现5,其它数字不会出现5for (int x = i; x % 5 == 0; x /= 5) {//统计这些因子中的5的个数。例如100这个因子,可以拆解为5*5*4.有两个5++ans;//5的个数}}return ans;}
}
数学优化:思路转变为求5的倍数的个数
| 解题思路:时间复杂度O( l o g 2 n log_2n log2n),空间复杂度O( 1 1 1) |
|---|
- 以1000为例:1000 = 5 ∗ 200 5*200 5∗200 = 5 ∗ 5 ∗ 40 5*5*40 5∗5∗40 = 5 ∗ 5 ∗ 5 ∗ 8 5*5*5*8 5∗5∗5∗8 = 5 ∗ 5 ∗ 5 ∗ 5 ∗ 8 5 5*5*5*5*\dfrac{8}{5} 5∗5∗5∗5∗58.则1000的阶乘的5的个数为200+40+8+1 = 249个
- 为什么对单个数字1000不断除5,可以求出1000的阶乘中5的个数呢?
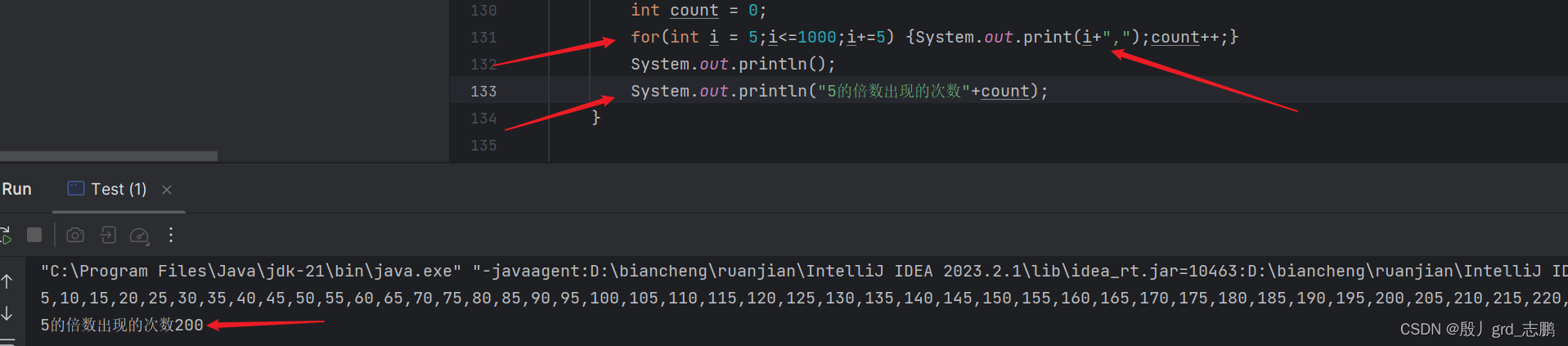
- 因为我们需要转变思路,从现在开始,我们要统计从1到1000中,5的倍数出现的次数。
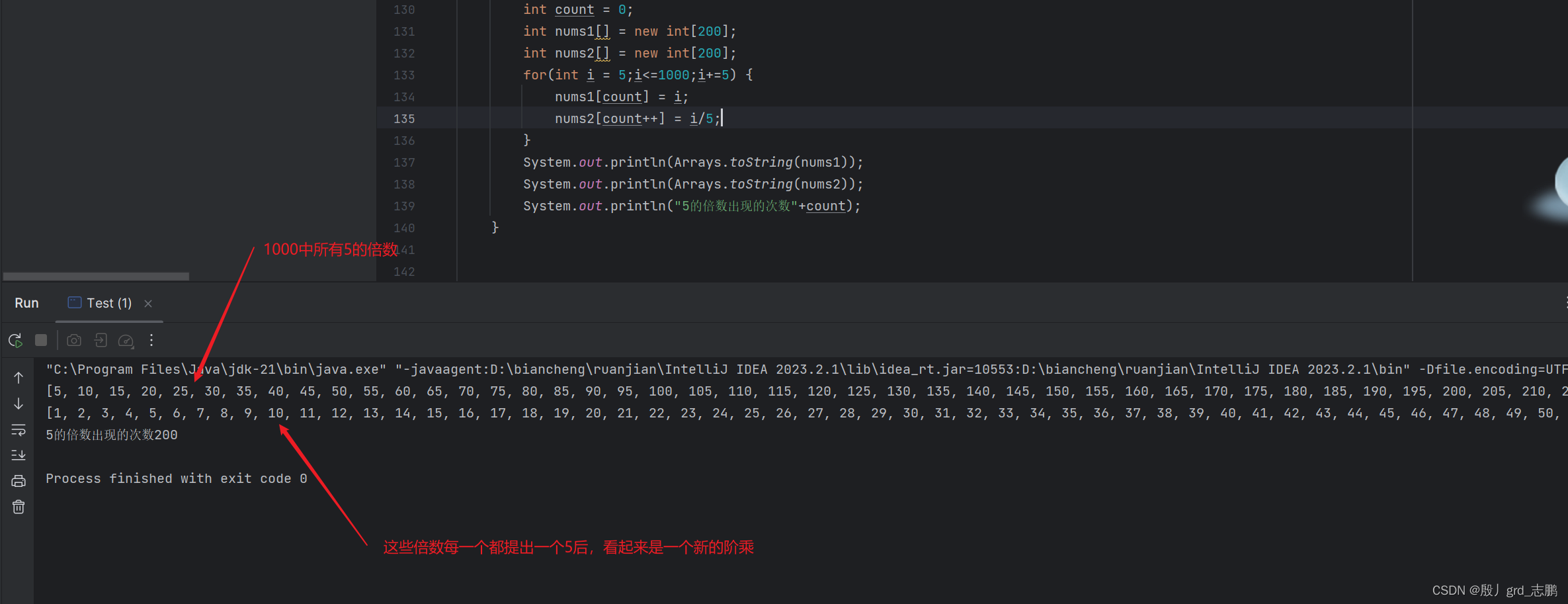
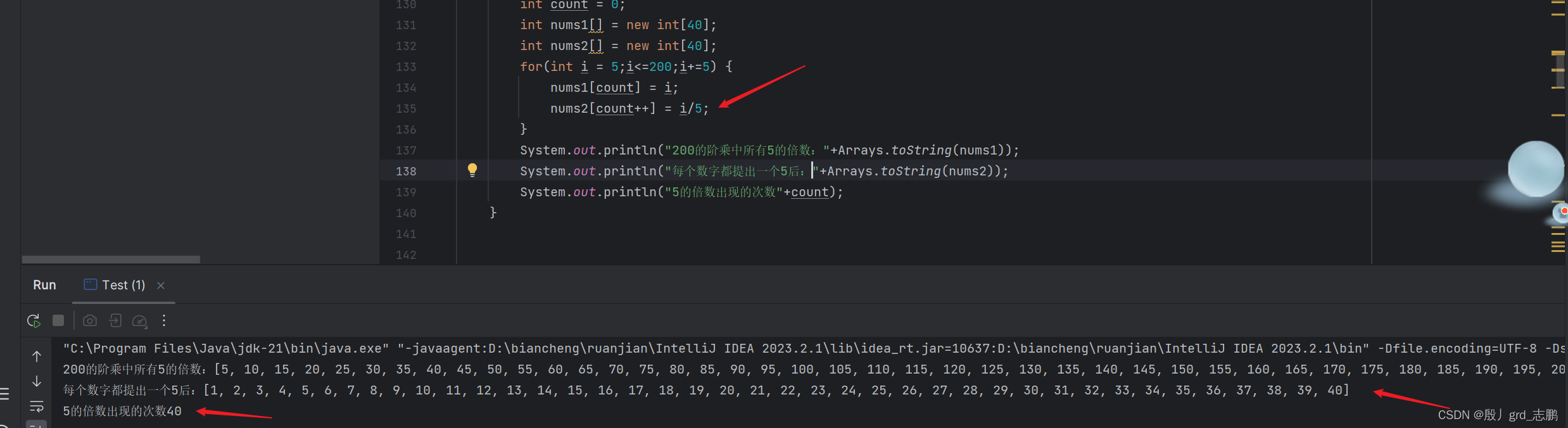
- 1到1000中,5的倍数出现200次, 200个5的倍数分别是 5 , 10 , 15 , 20 , . . . . . , 1000 5,10,15,20,.....,1000 5,10,15,20,.....,1000
- 此时如果我们将这200个5的倍数,全部提出一个5,就会获得200个5. 并且因式分解后剩下的值看起来如下: 1 ∗ 2 ∗ 3 ∗ 4 ∗ 5 ∗ . . . . ∗ 200 1*2*3*4*5*....*200 1∗2∗3∗4∗5∗....∗200,你会发现它们这些数正好组成了200的阶乘所有的数,
- 此时,我们只需要从1到200这些数中,找当中5的倍数的个数。也就是 5 , 10 , 15 , 20 , . . . , 200 5,10,15,20,...,200 5,10,15,20,...,200
- 而200这个阶乘中,5的倍数共出现40次,我们将40次进行统计,然后继续对这40个5的倍数提出一个5的因子。你会发现它们又变成了40的阶乘。
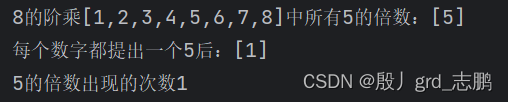
- 此时继续求40这个阶乘中,5的倍数出现的次数。结果如下:共8个5的倍数,我们将8个5提出后,剩下的数字组成了8的阶乘
- 继续对8求:共1个5的倍数5,提出1个5后,剩下数字只有1了,也就不用继续遍历了
- 最终,就可以将所有我们提出的5统计起来,200+40+8+1 = 249个。
| 代码 |
|---|
class Solution {public int trailingZeroes(int n) {int count = 0;//统计个数while (n != 0){//只要n的阶乘中还可以有5就继续n /= 5;//获取n这个阶乘中所有5的倍数的个数count += n;//统计个数}return count;}
}
相关文章:

java数据结构与算法刷题-----LeetCode172. 阶乘后的零
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 数学:阶乘的10因子个数数学优化:思路转变为求5的倍数…...
掌握数据相关性新利器:基于R、Python的Copula变量相关性分析及AI大模型应用探索
在工程、水文和金融等各学科的研究中,总是会遇到很多变量,研究这些相互纠缠的变量间的相关关系是各学科的研究的重点。虽然皮尔逊相关、秩相关等相关系数提供了变量间相关关系的粗略结果,但这些系数都存在着无法克服的困难。例如,…...
Centos7环境下安装MySQL8详细教程
1、下载mysql安装包 下载哪个版本,首先需要确定一下系统的glibc版本,使用如下命令: rpm -qa | grep glibc 2、检查是否安装过mysql ps:因为以前用yum安装过,所以先用yum卸载。如果不是此方式或者没安装过则跳过…...

趣学前端 | 综合一波CSS选择器的用法
背景 最近睡前习惯翻会书,重温了《HTML5与CSS 3权威指南》。这本书,分上下两册,之前读完了上册,下册基本没翻过。为了对得起花过的每一分钱,决定拾起来近期读一读。 CSS 选择器 在CSS3中,提倡使用选择器…...

数据库 06-04 恢复
01 一.事务故障 二.系统 三.磁盘 02. 重点是稳定存储器 组成...

基于MPPT的风力机发电系统simulink建模与仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 4.1风能与风力发电机模型 4.2风力机功率特性与最大功率点 4.3 MPPT 5.完整工程文件 1.课题概述 基于MPPT的风力机发电系统simulink建模与仿真。MPPT使用S函数编写实现。基于最大功率点跟踪(…...

GD32F30x IO 复用问题
1.PE9 复用PWM 引脚 需要使能 gpio_pin_remap_config(GPIO_TIMER0_FULL_REMAP,ENABLE);...
BPMNJS 在原生HTML中的引入与使用
BPMNJS 在HTML中的引入与使用 在网上看到的大多是基于vue使用BPMN的示例或者教程,竟然没有在HTML使用的示例,有也是很简单的介绍核心库的引入和使用,并没有涉及到扩展库。于是简单看了下,真的是一波三折,坎坎坷坷。不…...

HarmonyOS 应用开发之通过数据管理服务实现数据共享静默访问
场景介绍 典型跨应用访问数据的用户场景下,数据提供方会存在多次被拉起的情况。 为了降低数据提供方拉起次数,提高访问速度,OpenHarmony提供了一种不拉起数据提供方直接访问数据库的方式,即静默数据访问。 静默数据访问通过数据…...

ubuntu强密码支持
接到新需求,欧盟需要ubuntu使用强密码,网络上找到一个包可以增加ubuntu密码增强机制,以下是调试过程。 sudo apt-get install libpam-pwquality 然后,编辑位于/etc/pam.d/目录中的common-password文件: sudo vim /et…...

C语言中文分词 Friso的使用教程
Friso是使用C语言开发的一款高性能中文分词器,使用流行的mmseg算法实现。完全基于模块化设计和实现,可以很方便的植入到其他程序中,例如:MySQL,PHP等。同时支持对UTF-8/GBK编码的切分。 官方地址:https://…...

MySQL中drop、truncate和delete的区别
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏:每天一个知识点 ✨特色专栏:…...
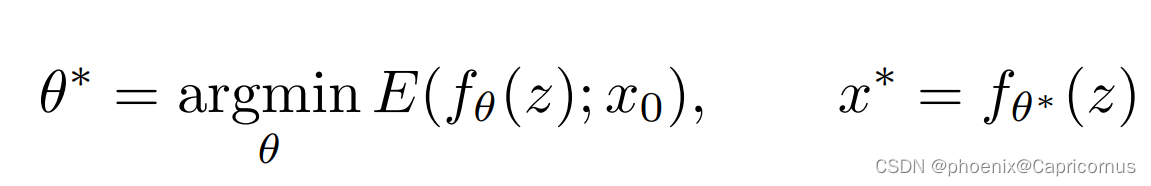
Deep Image Prior
自监督的开创性工作 从简单分布到复杂分布的映射,本质上是将重建限制到某一流形,在流形上通过观测图像的数据保真项作为监督。 称之为先验也是很准确,流形就是先验。 这个扰动也很关键,本质上一个平滑正则项。直观理解是各种扰动…...

leetcode148. 排序链表
方法1:插入方法进行改进 class Solution {public ListNode sortList(ListNode head) {/*想法:设置两个指针first,last分别指向当前有序子链表的头和尾节点;并遍历链表,当遍历到的节点值大于last的值时,就将该节点插入到有序子链表…...
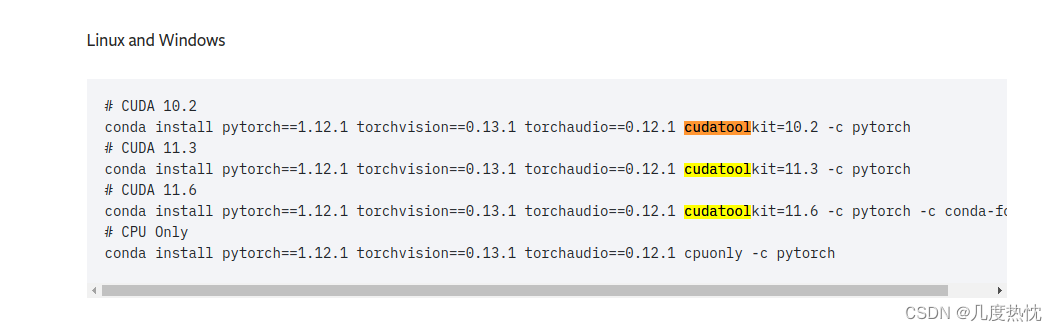
【深度学习环境配置】一文弄懂cuda,cudnn,NVIDIA Driver version,cudatoolkit的关系
【深度学习环境配置】一文弄懂cuda,cuDNN,NVIDIA Driver version,cudatoolkit的关系 NVIDIA Driver version(NVIDIA驱动程序)CUDAcuDNNcudatoolkit深度学习环境配置顺序 今天突然发现配置的环境有些问题,意…...

C语言中的字符与字符串:魔法般的函数探险
前言 在C语言的世界里,字符和字符串是两个不可或缺的元素,它们像是魔法般的存在,让文字与代码交织出无限可能。而在这个世界里,有一批特殊的函数,它们如同探险家,引领我们深入字符与字符串的秘境࿰…...
【JAVASE】带你了解面向对象三大特性之一(继承)
✅作者简介:大家好,我是橘橙黄又青,一个想要与大家共同进步的男人😉😉 🍎个人主页:再无B~U~G-CSDN博客 1.继承 1.1 为什么需要继承 Java 中使用类对现实世界中实体来…...
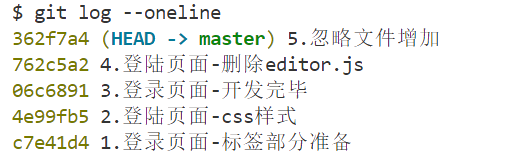
Git 如何去使用
目录 1. Git暂存区的使用 1.1. 暂存区的作用 1.2. 暂存区覆盖工作区(注意:完全确认覆盖时使用) 1.3. 暂存区移除文件 1.4. 练习 2. Git回退版本 2.1. 概念 2.2. 查看提交历史 2.3. 回退命令 2.4. 注意 3. Git删除文件 3.1. 需求 …...

C语言 | Leetcode C语言题解之第12题整数转罗马数字
题目: 题解: const char* thousands[] {"", "M", "MM", "MMM"}; const char* hundreds[] {"", "C", "CC", "CCC", "CD", "D", "DC"…...

【软件工程】测试规格
1. 引言 1.1简介 本次的测试用例是基于核心代码基本开发完毕,在第一代系统基本正常运行后编写的,主要目的是为了后续开发与维护的便利性。 该文档主要受众为该系统后续开发人员,并且在阅读此文档前最后先阅读本系统的需求文档、概要设计文…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...