政安晨:【深度学习神经网络基础】(三)—— 激活函数
目录
线性激活函数
阶跃激活函数
S型激活函数
双曲正切激活函数
修正线性单元
Softmax激活函数
偏置扮演什么角色?
政安晨的个人主页:政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: 政安晨的机器学习笔记
希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正!
本文目标:介绍激活函数。
在神经网络编程中,激活函数或传递函数为神经元的输出建立界限。神经网络可以使用许多不同的激活函数。我们将在本文中讨论最常见的激活函数。为神经网络选择激活函数是一个重要的考虑,因为它会影响输入数据格式化的方式。在本文中,我们将指导你选择激活函数。
线性激活函数
最基本的激活函数是线性函数,因为它根本不改变神经元输出。下面公式展示了程序通常如何实现线性激活函数:
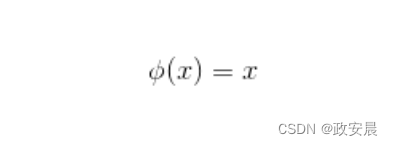
如你所见,这个激活函数只是返回神经元输入传递给它的值。下图展示了线性激活函数的图像。

为学习提供数值的回归神经网络,通常会在其输出层使用线性激活函数。分类神经网络,即为其输入确定合适类别的神经网络,通常在其输出层使用Softmax激活函数。
阶跃激活函数
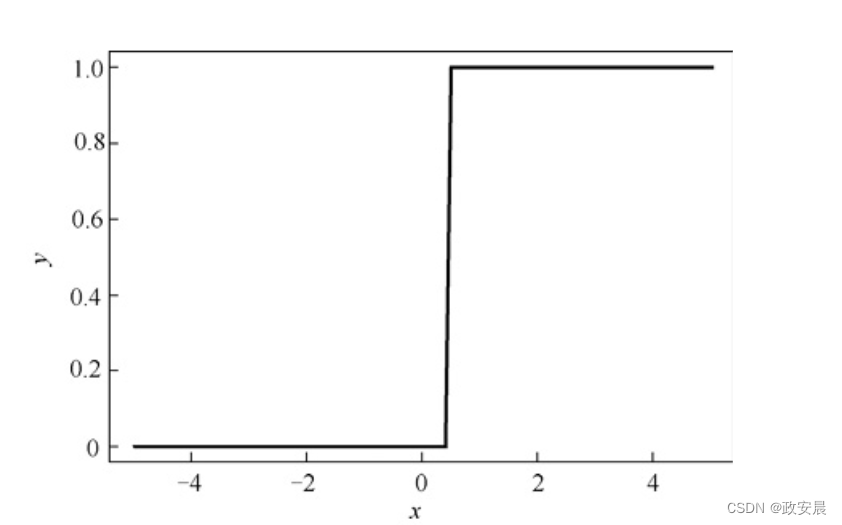
阶跃或阈值激活函数是另一种简单的激活函数。神经网络最初称为“感知机”(perceptron)。McCulloch和Pitts(1943)引入了最初的感知机,并使用了如下公式一样的阶跃激活函数:

上面公式为0.5或更高的输入值输出1,为所有其他输入值输出0。阶跃激活函数通常被称为阈值激活函数,因为它们仅对大于指定阈值的值返回1(真),如下图所示。
S型激活函数
对于仅需要输出正数的前馈神经网络,S型(Sigmoid)激活函数或逻辑激活函数是非常常见的选择。虽然它使用广泛,但双曲正切激活函数或ReLU激活函数通常是更合适的选择。我们将在后面介绍ReLU激活函数。下面公式展示了S型激活函数:
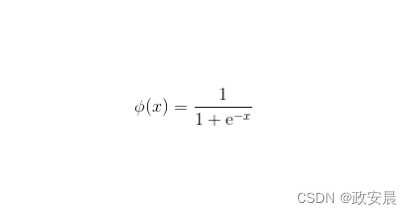
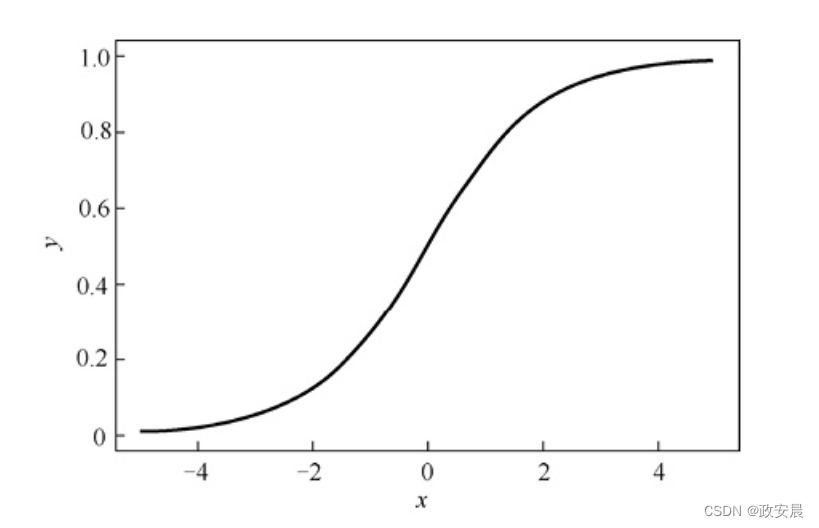
使用S型激活函数以确保值保持在相对较小的范围内,如下图所示,从图中可以看出,大于或小于0的值都会被压缩到0~1的范围内。
双曲正切激活函数
对于必须输出−1~1的值的神经网络,双曲正切(tanh)激活函数也是非常常见的激活函数,如下公式所示:

双曲正切激活函数图像的形状类似S型激活函数,图像的形状如下图所示:
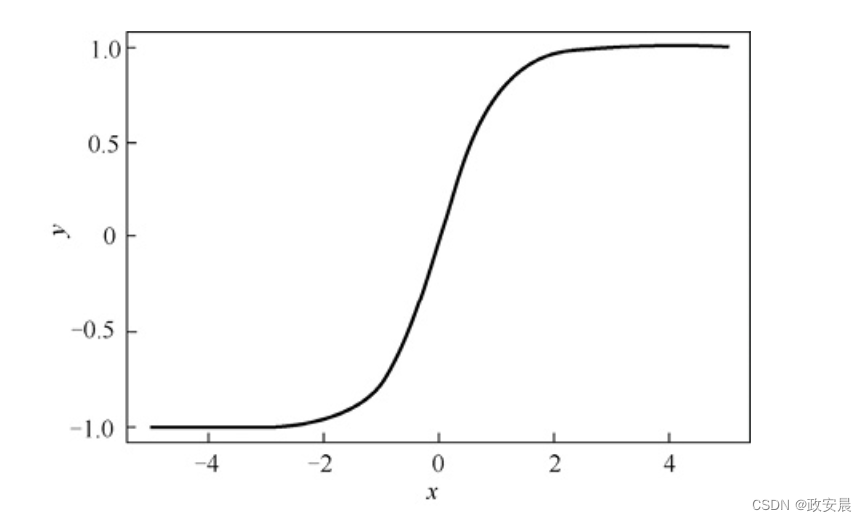
双曲正切激活函数相对S型激活函数具有诸多优点。这些优点涉及神经网络训练中使用的导数,我们以后在“反向传播训练”中介绍。
修正线性单元
修正线性单元(ReLU)由Teh和Hinton在2000年引入,在过去几年中得到了迅速的应用。在ReLU激活函数之前,双曲正切激活函数通常被视为优先选择的激活函数。由于出色的训练结果,目前大多数最新研究都推荐ReLU激活函数。因此,大多数神经网络应该在隐藏层上使用ReLU激活函数,在输出层上使用Softmax或线性激活函数。
下面公式展示了非常简单的ReLU激活函数:
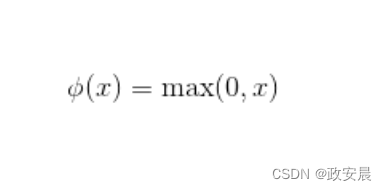
现在,我们将研究为什么ReLU激活函数通常比隐藏层的其他激活函数要好。性能提高的部分原因在于ReLU激活函数是线性的非饱和激活函数。与S型激活函数/逻辑激活函数或双曲正切激活函数不同,ReLU不会饱和到−1、0或1。饱和激活函数总是朝向并最终获得一个值。如双曲正切激活函数在x减小时饱和到−1,在x增大时饱和到1。
下图展示了ReLU激活函数的图像:
 最新研究表明,神经网络的隐藏层应使用ReLU激活函数。
最新研究表明,神经网络的隐藏层应使用ReLU激活函数。
Softmax激活函数
与线性激活函数一样,通常会在神经网络的输出层中找到Softmax激活函数。Softmax激活函数用于分类神经网络。分类神经网络中,具有最高值的神经元可以宣称神经网络的输入属于它的分类。因为它是一种更好的方法,所以Softmax激活函数会强制神经网络的输出表示输入落入每个类的概率。如果没有Softmax激活函数,则神经元的输出就是数值,值最高的数表示获胜的类。
为了了解如何使用Softmax激活函数,我们来研究一个常见的神经网络分类问题。
鸢尾花数据集包含针对150种不同鸢尾花的4个测量值。这些花中的每一种都属于3个鸢尾花物种之一。当你提供花朵的测量值时,Softmax激活函数允许神经网络为你提供这些测量值属于这3个物种的概率。如神经网络可能会告诉你,该鸢尾花有80%的概率是setosa,有15%的概率是virginica,只有5%的概率是versicolour。因为这些是概率,所以它们的总和必须是100%。不可能同时有80%的概率是setosa、75%的概率是virginica、20%的概率是versicolour——这种结果是毫无意义的。
要将输入数据分为3个鸢尾花物种之一,则对于这3个物种中的每一个,你都需要一个输出神经元。输出神经元并不指定这3个物种各自的概率。因此,我们期望提供的这些概率总和为100%。而神经网络将告诉你,花朵属于这3个物种中每一个的概率。
要获得概率,请使用下面公式中的Softmax函数:
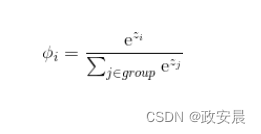
Softmax激活函数的计算方法与咱们前面介绍的其他激活函数不同。在使用Softmax作为激活函数时,单个神经元的输出取决于其他输出神经元。
下面是用伪代码实现了Softmax激活函数:
def softmax(neuron_output):sum = 0for v in neuron_output:sum = sum + vsum = math.exp(sum)proba = [ ]for i in range(len(neuron_output)):proba[i] = math.exp(neuron_output[i])/sum return proba请考虑一个训练好的神经网络,它将数据分为三类,如3个鸢尾花物种。在这种情况下,你将为每个目标分类使用一个输出神经元。请考虑神经网络要输出以下内容:
Neuron 1: setosa: 0.9
Neuron 2: versicolour: 0.2
Neuron 3: virginica: 0.4
从上面的输出中我们可以清楚地看到,神经网络认为数据代表了setosa鸢尾花。但是,这些值不是概率。值0.9不表示数据有90%的概率代表setosa。这些值的总和为1.5。要将它们视为概率,它们的总和必须为1。
该神经网络的输出向量如下:
[0.9, 0.2, 0.4]
如果将此向量提供给Softmax激活函数,则返回以下向量:
[0.47548495534876745, 0.2361188410001125, 0.28839620365112]
以上3个值的总和为1,可以视为概率。由于向量中的第一个值四舍五入为0.48(48%),因此数据表示setosa的概率为48%。你可以通过以下方式计算该值:
sum=exp(0.9)+exp(0.2)+exp(0.4)=5.17283056695839 j0=exp(0.9)/sum=0.47548495534876745 j1=exp(0.2)/sum=0.2361188410001125 j2=exp(0.4)/sum=0.28839620365112
偏置扮演什么角色?
在上文中看到的激活函数指定了单个神经元的输出。神经元的权重和偏置(bias)共同决定了激活的输出,以产生期望的输出。要查看这个过程如何发生,请考虑下面公式。它表示了单输入的S型激活神经网络:

变量x表示神经网络的单个输入。w和b变量指定了神经网络的权重和偏置。上面公式是一种组合,包含了指定神经网络的公式和指定S型激活函数的公式。
通过调整神经元的权重可以调整激活函数的斜率或形状。下图展示了权重变化对S型激活函数输出的影响:
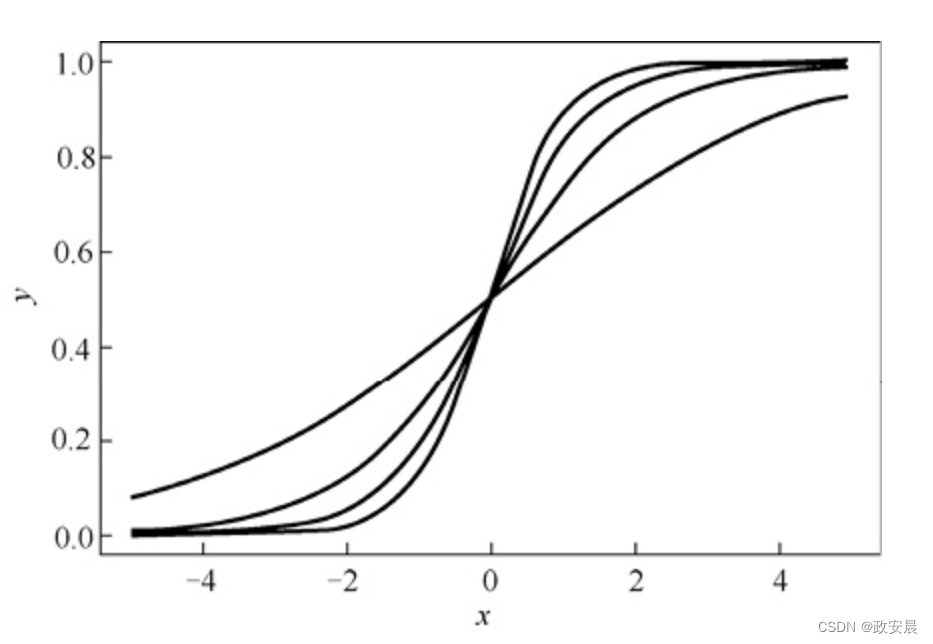
下图展示了使用以下参数的多个S型曲线:
f(x, 0.5, 0.0)
f(x, 1.0, 0.0)
f(x, 1.5, 0.0)
f(x, 2.0, 0.0)
为了生成这些曲线,我们没有使用偏置,这很显然,因为每种情况下第3个参数都是0。使用4个权重值会在上图中产生4条不同的S型曲线。无论权重如何,当x为0时我们总是得到相同的值0.5,因为当x为0时所有曲线都到达同一点。当输入接近0.5时,我们可能需要神经网络产生其他值。
调整偏置会使S型曲线发生移动,这使得当x接近0时,该函数取值不为0.5。下图展示了权重为1.0时,偏置变化对S型激活函数输出的影响。
下图展示了具有以下参数的多条S型曲线:
f(x, 1.0, 1.0)
f(x, 1.0, 0.5)
f(x, 1.0, 1.5)
f(x, 1.0, 2.0)
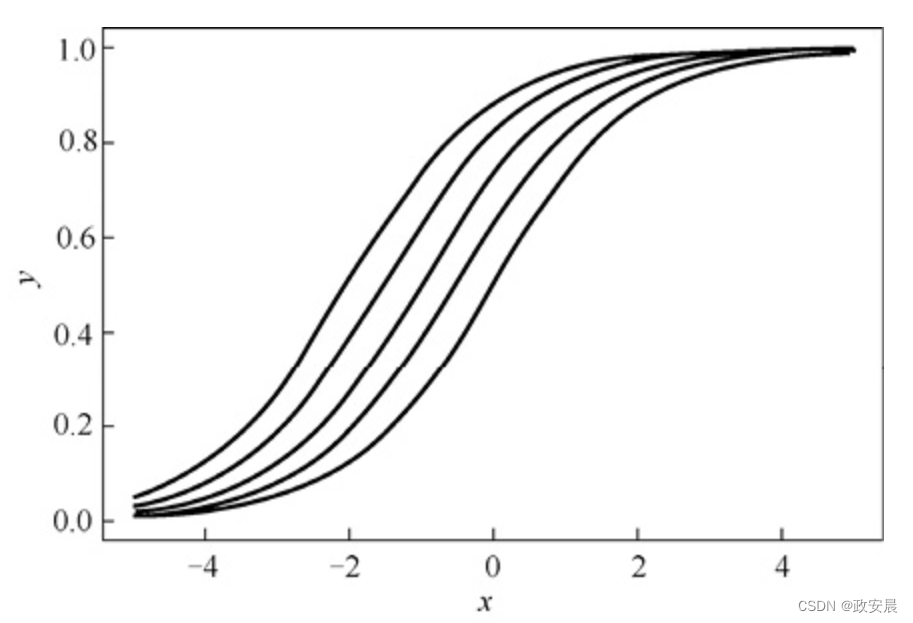
这些函数的权重均为1.0。当我们调整不同的偏置时,S型曲线向左或向右移动。由于所有曲线在右上角或左下角发生合并,因此并不是完全的移位。当我们将偏置和权重放在一起时,它们生成了一条曲线,该曲线创建了神经元所需的输出。
以上曲线仅是一个神经元的输出。在一个完整的神经网络中,许多不同神经元的输出将合并,以产生复杂的输出模式。
相关文章:

政安晨:【深度学习神经网络基础】(三)—— 激活函数
目录 线性激活函数 阶跃激活函数 S型激活函数 双曲正切激活函数 修正线性单元 Softmax激活函数 偏置扮演什么角色? 政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: 政安晨的机器学习笔记 希望政安晨的博客能够对您有所裨…...
使用tomcat里的API - servlet 写动态网页
一、创建一个新的Maven空项目 首次创建maven项目的时候,会自动从maven网站上下载一些依赖组件(这个过程需要保证网络稳定,否则后续打包一些操作会出现一些问题) ps:校园网可能会屏蔽一些网站,可能会导致maven的依赖…...
从0到1搭建文档库——sphinx + git + read the docs
sphinx git read the docs 目录 一、sphinx 1 sphinx的安装 2 本地构建文件框架 1)创建基本框架(生成index.rst ;conf.py) conf.py默认内容 index.rst默认内容 2)生成页面(Windows系统下…...

EasyExcel 校验后导入
引入pom <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.3.3</version></dependency>触发校验类 import com.baomidou.mybatisplus.extension.api.R; import lombok.experimental…...

【星计划★C语言】c语言初相识:探索编程之路
🌈个人主页:聆风吟_ 🔥系列专栏:星计划★C语言、Linux实践室 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️第一个c语言程序二. ⛳️数据类型2.1 🔔数据单位2.2 &…...

搜维尔科技:借助 ARVR 的力量缩小现代制造业的技能差距
借助ARVR的力量缩小现代制造业的技能差距 搜维尔科技:Senseglove案例-扩展机器人技术及其VR应用...
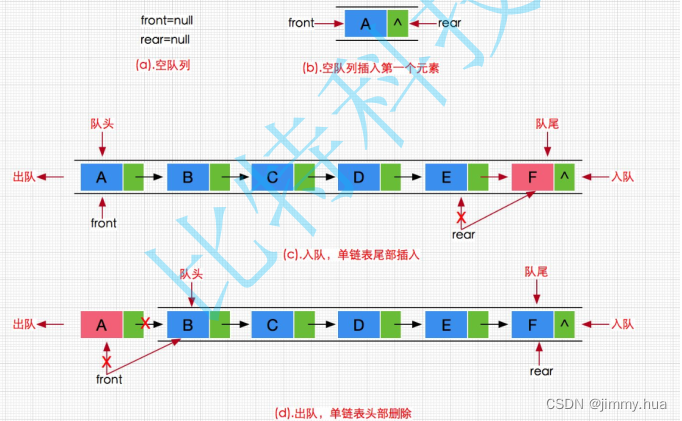
数据结构之栈和队列
1.前言 大家好久不见,这段时间由于忙去了。就没有即使维护我的博客,先给大家赔个不是。 我们还是规矩不乱,先赞后看~ 今天讲的内容是数据结构中非常重要的一个部分:栈和队列。它在今后的学习中也会再次出现(c&#…...
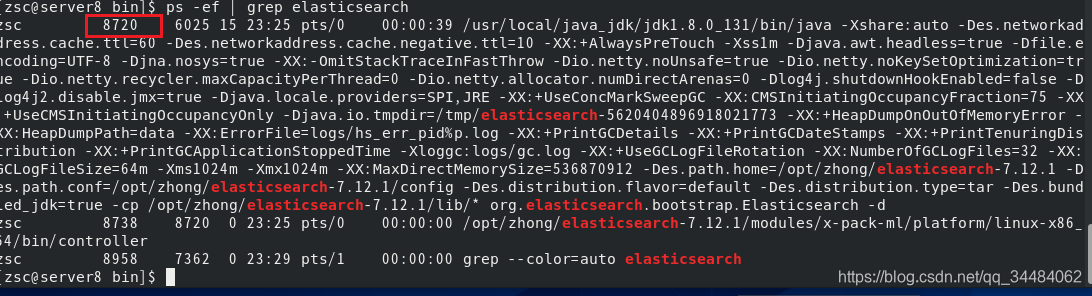
centos安装使用elasticsearch
1.首先可以在 Elasticsearch 官网 Download Elasticsearch | Elastic 下载安装包 2. 在指定的位置(我的是/opt/zhong/)解压安装包 tar -zxvf elasticsearch-7.12.1-linux-x86_64.tar.gz 3.启动es-这种方式启动会将日志全部打印在当前页面,一旦使用 ctrlc退出就会导…...
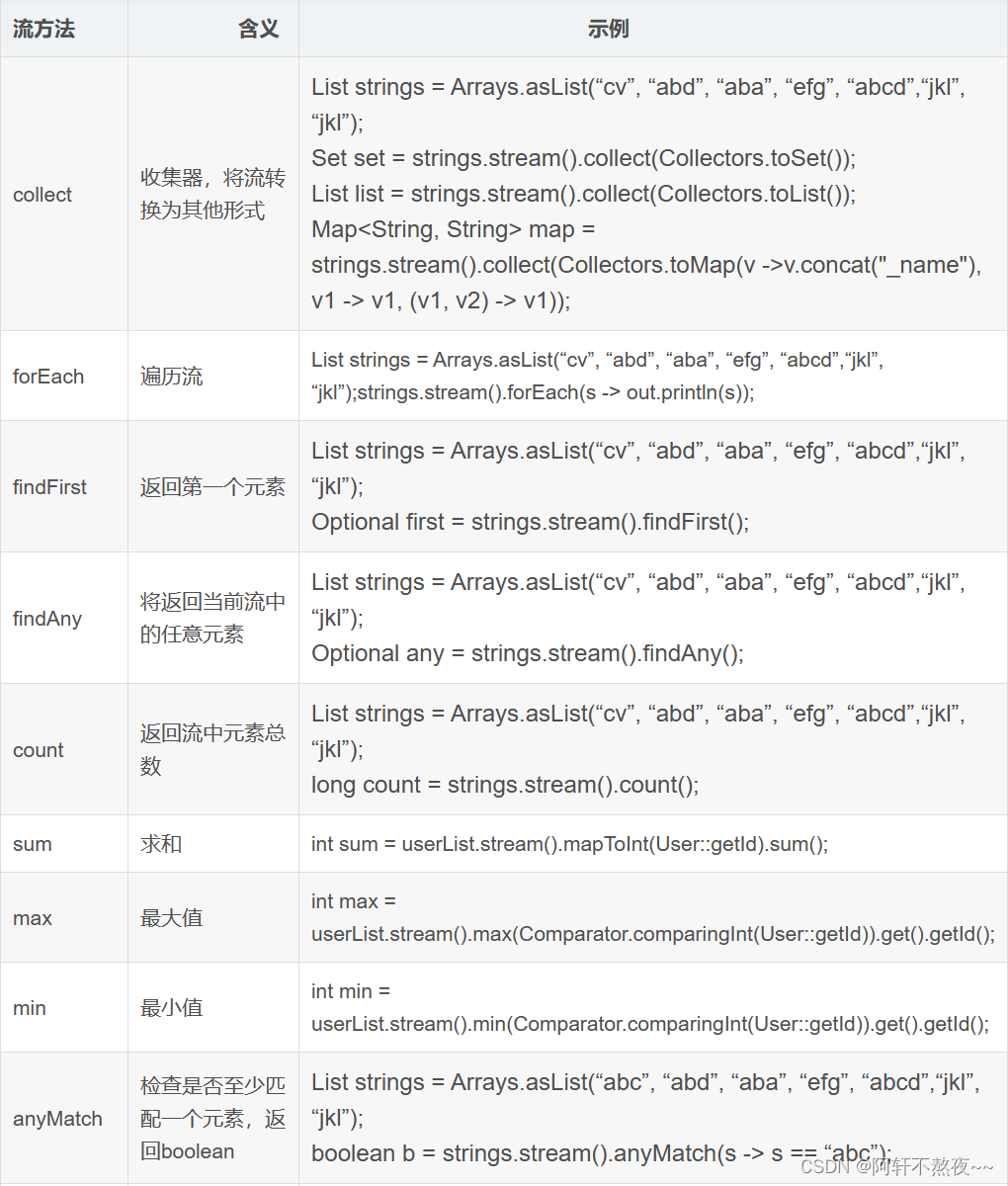
4.7学习总结
java学习 一.Stream流 (一.)概念: Stream将要处理的元素集合看作一种流,在流的过程中,借助Stream API对流中的元素进行操作,比如:筛选、排序、聚合等。Stream流是对集合(Collection)对象功能的增强&…...
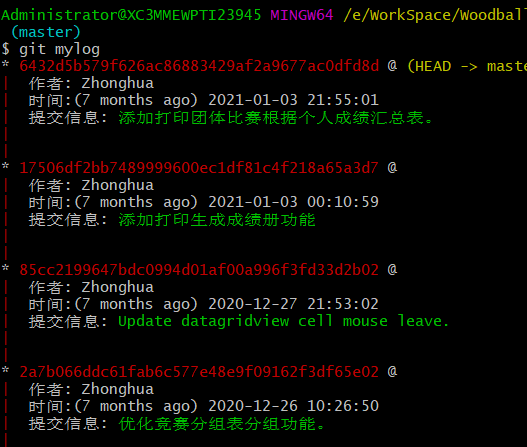
自定义gitlog格式
git log命令非常强大而好用,在复杂系统的版本管理中扮演着重要的角色,但默认的git log命令显示出的东西实在太丑,不好好打扮一下根本没法见人,打扮好了用alias命令拍个照片,就正式出道了! 在使用git查看lo…...

Redission--分布式锁
Redission的锁的好处 Redission分布式锁的底层是setnx和lua脚本(保证原子性) 1.是可重入锁。 2.Redisson 锁支持自动续期功能,这可以帮助我们合理控制分布式锁的有效时长,当业务逻辑执行时间超出了锁的过期时间,锁会自动续期,避免…...

非关系型数据库(缓存数据库)redis的集群
目录 一.群集模式——Cluster 1.原理 2.作用 3.特点 4.工作机制 哈希槽 哈希槽的分配 哈希槽可按照集群主机数平均分配(默认分配) 根据主机的性能以及功能自定义分配 redis集群的分片 分片 如何找到给定key的分片 优势 二. 搭建Redis群集…...
)
MySQL:表的约束(上)
文章目录 空属性默认值列描述zerofill主键 本篇总结的是MySQL中关于表的约束部分的内容 空属性 在进行表的创建时,会有两个值,null和not null,而数据库默认的字段基本都是空,但是在实际的开发过程中要保证字段不能为空ÿ…...
树莓派5使用体验
原文地址:树莓派5使用体验 - Pleasure的博客 下面是正文内容: 前言 好久没有关于教程方面的博文了,由于最近打算入门嵌入式系统,所以就去购入了树莓派5开发板 树莓派5是2023年10月23日正式发售的,过去的时间不算太远吧…...

代码随想录算法训练营第42天| 背包问题、416. 分割等和子集
01 背包 题目描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 二维dp数组01背包: 确定dp数组以及下标的含义 …...

Node.js安装及环境配置指南
Node.js安装及环境配置指南 一、Node.js的安装 安装Node.js之前,首先需要确保你的电脑已经安装了合适的编译器和开发环境。Node.js是一个开源的、跨平台的JavaScript运行环境,它使得JavaScript可以在服务器端运行。 下载Node.js安装包 访问Node.js的…...
【Java基础】面试题汇总
Java基础面试题1. JVM vs JDK vs JRE 2. 什么是字节码?采用字节码的好处是什么?3. 为什么说 Java 语言“编译与解释并存”?4. AOT 有什么优点?为什么不全部使用 AOT 呢?5. Java 和 C 的区别?6. Java 中的基本数据类型࿱…...
)
数据库事务的超级详细讲解,包括事务特性、事务隔离级别、MVCC(多版本并发控制)
数据库事务: 主要有事务特性,事务的隔离级别,MVCC。 事务特性: 事务(Transaction)是指作为单个逻辑工作单元执行的一系列操作,这些操作要么全部成功执行,要么全部不执行ÿ…...

鸿蒙Lottie动画-实现控制动画的播放、暂停、倍速播放、播放顺序
介绍 本示例展示了lottie对动画的操作功能。引入Lottie模块,实现控制动画的播放、暂停、倍速播放、播放顺序、播放到指定帧停止或从指定帧开始播放、侦听事件等功能,动画资源路径必须是json格式。 效果预览 使用说明: 进入页面默认开始201…...

C++面试100问与自动驾驶100问
C的学习和面试其实是非常的不友好的,首先C的学习内容非常的多,其次C的面试不单单面试C的知识点,还有它的“七大姑八大姨”(计算机网络、数据结构、算法、计算机组成原理、操作系统、编译、xxx的底层实现 and so on)。 …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
