当前位置： 首页 > news >正文

鸿蒙原生应用已超4000个！

news 2026/2/8 9:23:09

鸿蒙原生应用已超4000个！

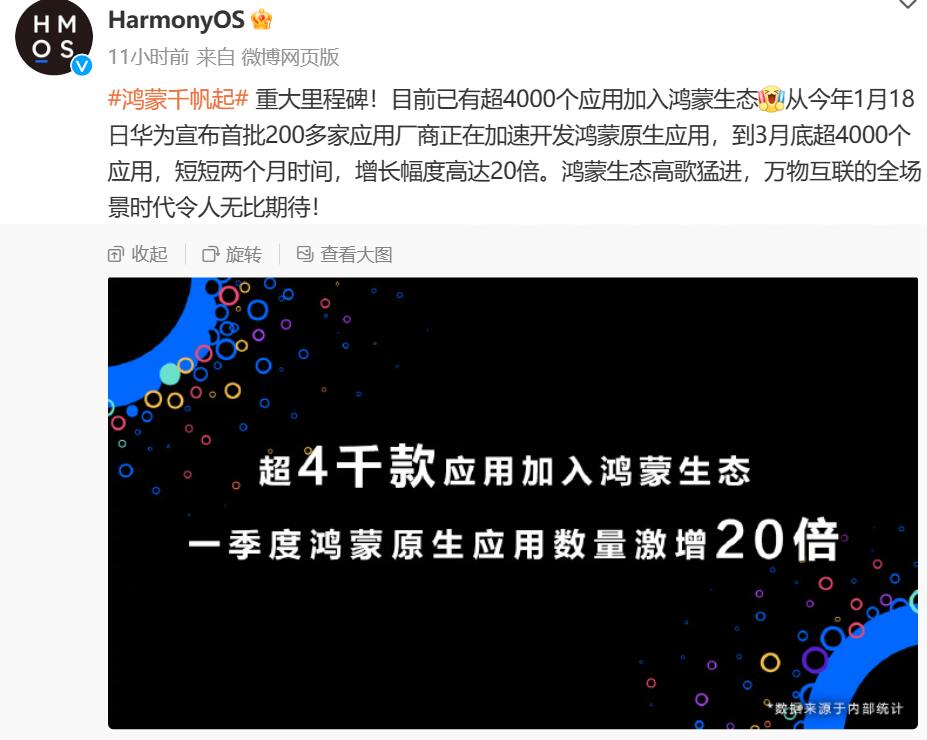
来自 HarmonyOS  微博近期消息，#鸿蒙千帆起# 重大里程碑！目前已有超4000个应用加入鸿蒙生态。从今年1月18日华为宣布首批200多家应用厂商正在加速开发鸿蒙原生应用，到3月底超4000个应用，短短两个月时间，增长幅度高达20倍。鸿蒙生态高歌猛进，万物互联的全场景时代令人无比期待！

https://img1.sycdn.imooc.com/66129b100001269e09270740.jpg

#HarmonyOS NEXT#

#HarmonyOS#市场或迎来爆发式增长！  https://www.imooc.com/article/344180

#世界读书日#，学习鸿蒙正当时！

  • 《跟老卫学 HarmonyOS 开发》 开源免费教程：https://github.com/waylau/harmonyos-tutorial

  • 《鸿蒙 HarmonyOS 手机应用开发实战》（清华大学出版社）：https://waylau.com/about-harmonyos-mobile-application-development-book/

  • 《鸿蒙 HarmonyOS 应用开发从入门到精通战》（北京大学出版社）：https://github.com/waylau/harmonyos-tutorial

  • “鸿蒙系统实战短视频 App 从 0 到 1 掌握 HarmonyOS” ：https://coding.imooc.com/class/674.html

  • 《鸿蒙HarmonyOS应用开发入门》（清华大学出版社）：https://waylau.com/about-harmonyos-3-tutorial-book/

​

相关文章：

鸿蒙原生应用已超4000个！

鸿蒙原生应用已超4000个！ 来自 HarmonyOS 微博近期消息，#鸿蒙千帆起# 重大里程碑！目前已有超4000个应用加入鸿蒙生态。从今年1月18日华为宣布首批200多家应用厂商正在加速开发鸿蒙原生应用，到3月底超4000个应用，短短…...

编程日记 2024/4/8 13:38:37

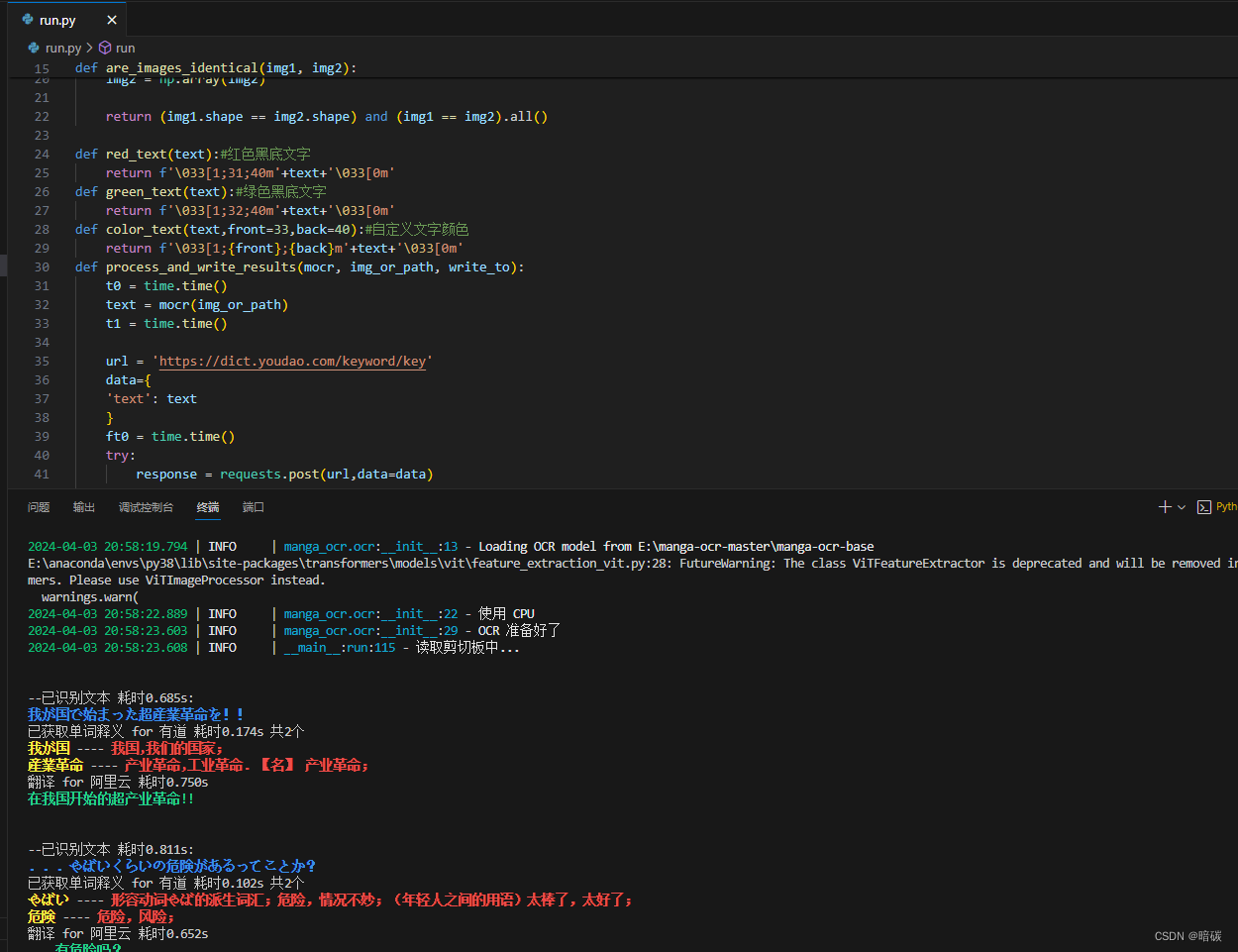
manga-ocr漫画日文ocr

github 下载 解压 anaconda新建环境 conda create -n manga_ocr python3.8 激活环境 conda activate manga_ocr cd到解压目录 cd /d manga-ocr-master 安装依赖包 pip install -r requirements.txt pip3 install manga-ocr 下载离线model huggingface 123云盘 解压到一个目录…...

编程日记 2024/4/8 13:36:35

STL、Vector和Set的讲解和例题分析

STL STL（Standard Template Library，标准模板库）是C标准库的一部分，它提供了一系列通用的编程组件，包括容器、迭代器、算法和函数对象等。STL是C中实现泛型编程的核心，它允许程序员使用模板编写与数…...

编程日记 2024/4/8 13:34:33

Android 13 aosp hiddenapi config

Android 11 hiddenapi路径 frameworks/base/config/hiddenapi-greylist-packages.txtAndroid 13 hiddenapi路径 frameworks/base/boot/hiddenapi/hiddenapi-unsupported-packages.txt...

编程日记 2024/4/8 13:33:31

数据仓库面试总结

文章目录 1.什么是数据仓库？2.ETL是什么？3.数据仓库和数据库的区别（OLTP和OLAP的区别）4.数据仓库和数据集市的区别5.维度分析5.1 什么是维度？5.2什么是指标？ 6.什么是数仓建模？7.事实表7.维度表…...

编程日记 2024/4/8 13:31:30

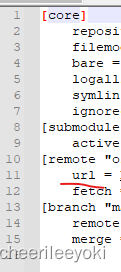
git Failed to connect to 你的网址 port 8282: Timed out

git Failed to connect to 你的网址 port 8282: Timed out 出现这个问题的原因是：原来的仓库换了网址，原版网址不可用了。 解决方法如下： 方法一：查看git用户配置是否有如下配置 http.proxyhttp://xxx https.proxyhttp://xxx如果…...

编程日记 2024/4/8 13:30:28

[C++][算法基础]堆排序(堆)

输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。 输入格式 第一行包含整数 n 和 m。 第二行包含 n 个整数，表示整数数列。 输出格式 共一行，包含 m 个整数，表示整数数列中前 m 小的数。 数据范围 1≤m≤n≤&#x…...

编程日记 2024/4/8 13:29:27

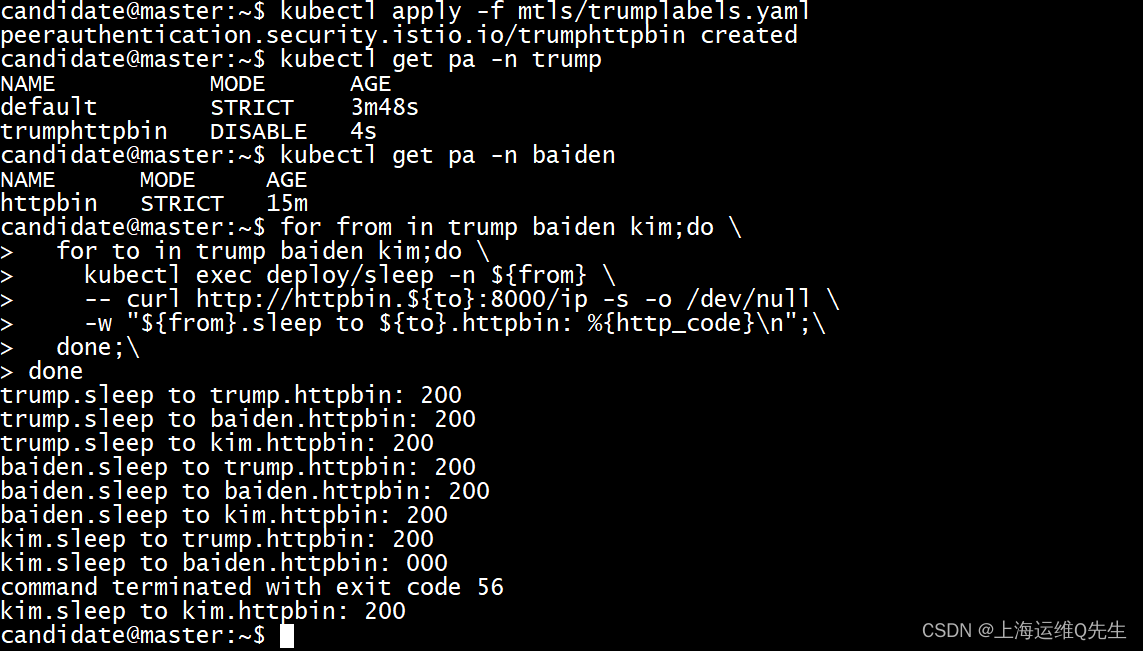
备考ICA----Istio实验15---开启 mTLS 自动双向认证实验

备考ICA----Istio实验15—开启mTLS自动双向认证实验 在某些生成环境下,我们希望微服务和微服务之间使用加密通讯方式来确保不被中间人代理. 默认情况下Istio 使用 PERMISSIVE模式配置目标工作负载,PERMISSIVE模式时,服务可以使用明文通讯.为了只允许双向 TLS 流量，…...

编程日记 2024/4/8 13:28:26

Hive SchemaTool 命令详解

Hive schematool 是 hive 自带的管理 schema 的相关工具。 列出详细说明 schematool -help直接输入 schematool 或者schematool -help 输出结果如下&#xff1a; usage: schemaTool-alterCatalog <arg> Alter a catalog, requires--catalogLocation an…...

编程日记 2024/4/8 13:27:24

51单片机入门_江协科技_17~18_OB记录的笔记

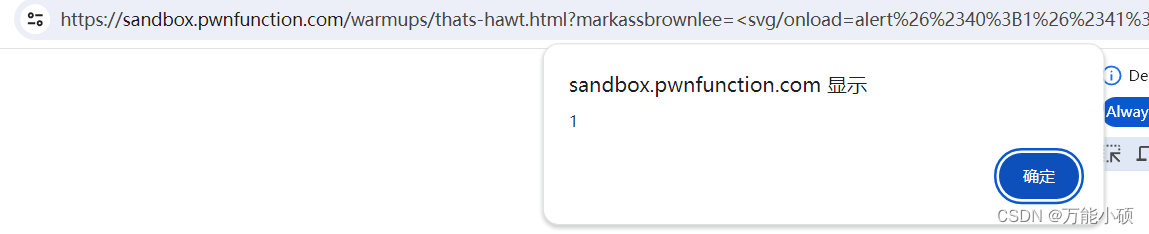
17. 定时器 17.1. 定时器介绍&#xff1a;51单片机的定时器属于单片机的内部资源&#xff0c;其电路的连接和运转均在单片机内部完成&#xff0c;无需占用CPU外围IO接口&#xff1b; 定时器作用&#xff1a; &#xff08;1&#xff09;用于计时系统&#xff0c;可实现软件计时&…...

编程日记 2024/4/8 13:26:23

xss.pwnfunction-Ah That‘s Hawt

<svg/onloadalert%26%2340%3B1%26%2341%3B> <svg/>是一个自闭合形式 &#xff0c;当页面或元素加载完成时&#xff0c;onload 事件会被触发&#xff0c;从而可以执行相应的 JavaScript 函数...

编程日记 2024/4/8 13:24:22

Python学习从0开始——005数据结构

Python学习从0开始——005数据结构 一、列表list二、元组和序列三、集合四、字典五、循环技巧六、条件控制七、序列和其它类型的比较 一、列表list 不是所有数据都可以排序或比较。例如&#xff0c;[None, ‘hello’, 10] 就不可排序&#xff0c;因为整数不能与字符串对比&…...

编程日记 2024/4/8 13:22:19

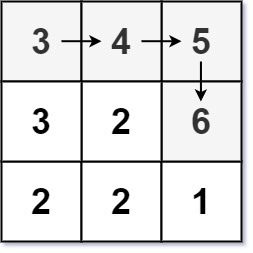
力扣每日一题：LCR112--矩阵中的最长递增路径

题目 给定一个 m x n 整数矩阵 matrix &#xff0c;找出其中 最长递增路径 的长度。 对于每个单元格&#xff0c;你可以往上&#xff0c;下&#xff0c;左&#xff0c;右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外&#xff08;即不允许环绕&#xff09;。 示例…...

编程日记 2024/4/8 13:21:18

树莓派部署yolov5实现目标检测（ubuntu22.04.3）

最近两天搞了一下树莓派部署yolov5&#xff0c;有点难搞&#xff08;这个东西有点老&#xff0c;版本冲突有些包废弃了等等&#xff09; 最后换到ubuntu系统弄了&#xff0c;下面是我的整体步骤&#xff08;建议先使能一下ssh&#xff08;最下面有&#xff09;&#xff0c;结合…...

编程日记 2024/4/8 13:19:16

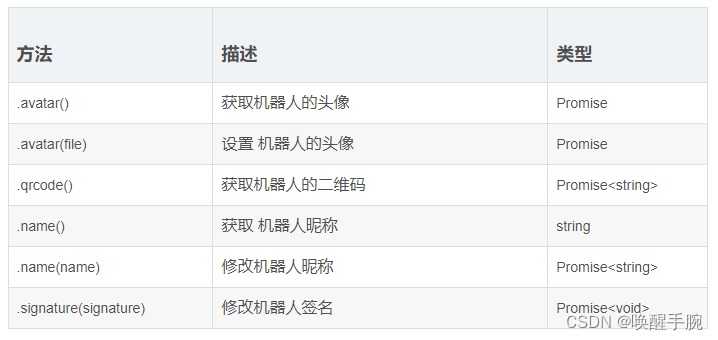
2024 年最新使用 Wechaty 开源框架搭建部署微信机器人（微信群智能客服案例）

读取联系人信息 获取当前机器人账号全部联系人信息 bot.on(ready, async () > {console.log("机器人准备完毕&#xff01;&#xff01;&#xff01;")let contactList await bot.Contact.findAll()for (let index 0; index < contactList.length; index) {…...

编程日记 2024/4/8 13:18:15

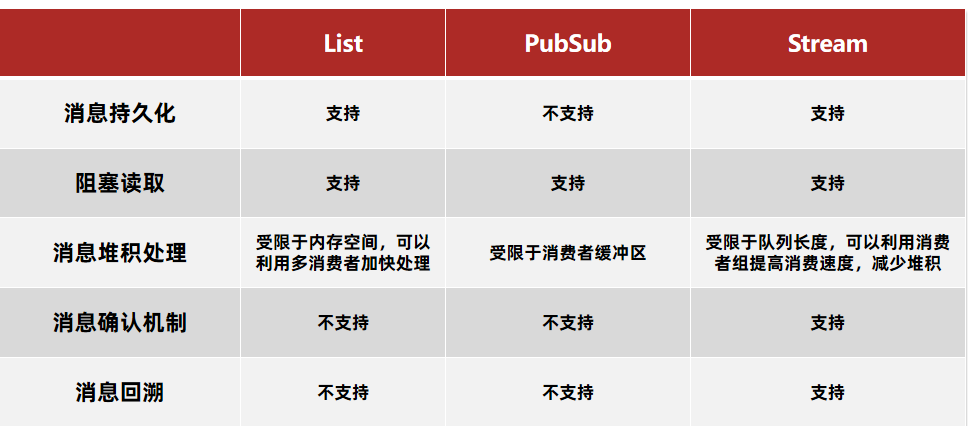
Redis从入门到精通(九)Redis实战(六)基于Redis队列实现异步秒杀下单

↑↑↑请在文章开头处下载测试项目源代码↑↑↑ 文章目录 前言4.5 分布式锁-Redisson4.5.4 Redission锁重试4.5.5 WatchDog机制4.5.5 MutiLock原理 4.6 秒杀优化4.6.1 优化方案4.6.2 完成秒杀优化 4.7 Redis消息队列4.7.1 基于List实现消息队列4.7.2 基于PubSub的消息队列4.7.…...

编程日记 2024/4/8 13:17:13

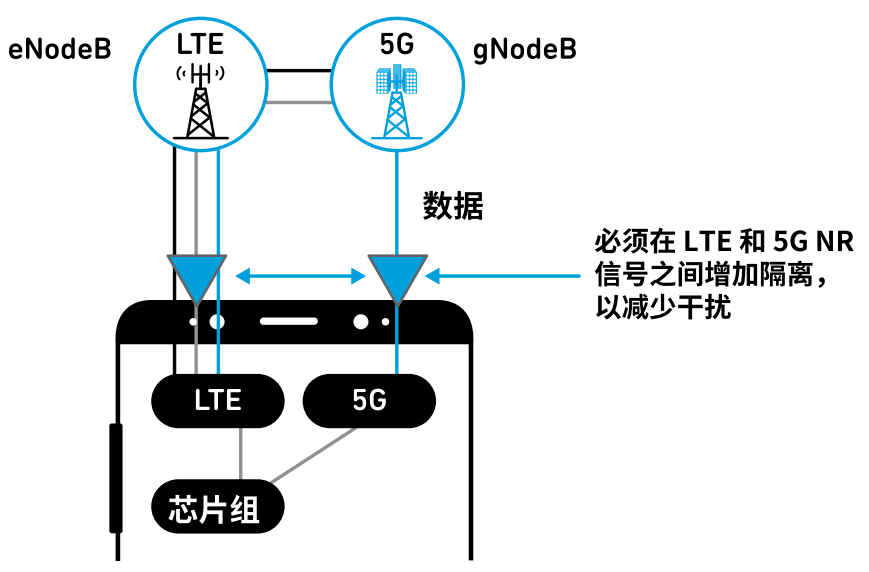
什么是多路复用器滤波器

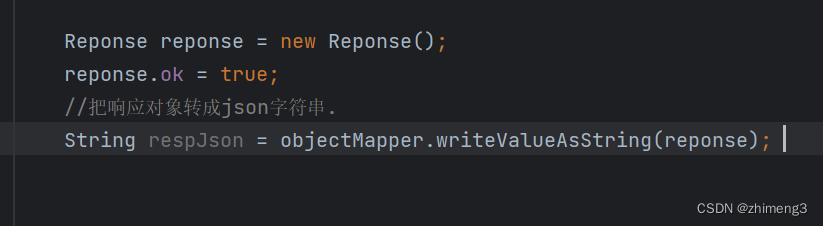
本章将更深入地介绍多路复用器滤波器&#xff0c;以及它们如何用于各种应用中。您将了解到多路复用器如何帮助设计人员创造出更复杂的无线产品。 了解多路复用器 多路复用器是一组射频(RF)滤波器&#xff0c;它们组合在一起&#xff0c;但不会彼此加载&#xff0c;可以在输出之…...

编程日记 2024/4/8 13:15:11

Severt和tomcat的使用(补充）

打包程序 在pom.xml中添加上述代码之后打包时会生成war包并且包的名称是test 默认情况打的是jar包.jar里量但是tomcat要求的是war包. war包Tomcat专属的压缩包. war里面不光有.class还有一些tomcat要求的配置文件(web.xml等)还有前端的一些代码(html, css, js) 点击其右边的m…...

编程日记 2024/4/8 13:14:10

JavaEE初阶——多线程(一)

T04BF &#x1f44b;专栏: 算法|JAVA|MySQL|C语言 &#x1faf5; 小比特 大梦想 此篇文章与大家分享多线程的第一部分:引入线程以及创建多线程的几种方式 此文章是建立在前一篇文章进程的基础上的 如果有不足的或者错误的请您指出! 1.认识线程 我们知道现代的cpu大多都是多核心…...

编程日记 2024/4/8 13:11:07

MongoDB主从复制模式基于银河麒麟V10系统

MongoDB主从复制模式基于银河麒麟V10系统 背景介绍 MongoDB自4.0版本开始已经不再建议使用传统的master/slave复制架构，而是全面采用了复制集（Replica Sets）作为标准的复制和高可用性解决方案。 复制集是MongoDB的一种数据复制和高可用性机制，通过异步同步数据至多个服务…...

编程日记 2024/4/8 13:10:05

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

超短脉冲激光自聚焦效应

前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应&#xff0c;这是一种非线性光学现象&#xff0c;主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场&#xff0c;对材料产生非线性响应&#xff0c;可能…...

编程新知 2026/2/4 16:43:14

Prompt Tuning、P-Tuning、Prefix Tuning的区别

一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning（提示调优） 核心思想：固定预训练模型参数，仅学习额外的连续提示向量（通常是嵌入层的一部分）。实现方式：在输入文本前添加可训练的连续向量（软提示），模型只更新这些提示参数。优势：参数量少（仅提…...

编程新知 2026/2/8 1:14:13

【网络安全产品大调研系列】2. 体验漏洞扫描

前言 2023 年漏洞扫描服务市场规模预计为 3.06&#xff08;十亿美元&#xff09;。漏洞扫描服务市场行业预计将从 2024 年的 3.48&#xff08;十亿美元&#xff09;增长到 2032 年的 9.54&#xff08;十亿美元&#xff09;。预测期内漏洞扫描服务市场 CAGR&#xff08;增长率&…...

编程新知 2026/2/4 12:43:08

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力

引言&#xff1a; 在人工智能快速发展的浪潮中&#xff0c;快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型&#xff08;LLM&#xff09;。该模型代表着该领域的重大突破&#xff0c;通过独特方式融合思考与非思考…...

编程新知 2026/2/6 19:29:20

【SQL学习笔记1】增删改查+多表连接全解析（内附SQL免费在线练习工具）

可以使用Sqliteviz这个网站免费编写sql语句&#xff0c;它能够让用户直接在浏览器内练习SQL的语法&#xff0c;不需要安装任何软件。 链接如下&#xff1a; sqliteviz 注意&#xff1a; 在转写SQL语法时&#xff0c;关键字之间有一个特定的顺序&#xff0c;这个顺序会影响到…...

编程新知 2026/2/5 4:36:53

React---day11

14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store&#xff1a; 我们在使用异步的时候理应是要使用中间件的&#xff0c;但是configureStore 已经自动集成了 redux-thunk&#xff0c;注意action里面要返回函数 import { configureS…...

编程新知 2026/1/19 2:13:24

JVM 内存结构 详解

内存结构 运行时数据区&#xff1a; Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器&#xff1a; ​ 线程私有&#xff0c;程序控制流的指示器&#xff0c;分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 ​ 每个线程都有一个程序计数…...

编程新知 2026/2/6 3:24:58

嵌入式学习笔记DAY33（网络编程——TCP）

一、网络架构 C/S &#xff08;client/server 客户端/服务器&#xff09;&#xff1a;由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序&#xff0c;负责提供用户界面和交互逻辑 &#xff0c;接收用户输入&#xff0c;向服务器发送请求&#xff0c;并展示服务…...

编程新知 2026/2/7 11:00:30

面向无人机海岸带生态系统监测的语义分割基准数据集

描述&#xff1a;海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而&#xff0c;目前该领域仍面临一个挑战&#xff0c;即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

编程新知 2026/1/25 14:15:52