2024年第十七届 认证杯 网络挑战赛 (A题)| 保暖纤维的保暖能力 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。
让我们来看看认证杯 网络挑战赛 (A题)!
CS团队倾注了大量时间和心血,深入挖掘解决方案。通过热传导、梯度提升等算法,设计了明晰的项目,耗费时间确保可行性。为客户选择了最适项目,以数据支持、文献分析和可视化手段深刻展示思路。这综合团队努力体现在每个步骤,确保方案既创新又可行,为大家提供了全面而深入的洞见噢~
完整内容可以在文章末尾领取!

假设衣物内填充的保暖纤维为一组纤维,每根纤维的保暖能力与其长度、直径、密度、热导率等因素有关。为了综合考虑这些因素,我们可以建立如下的指标体系:
- 纤维密度:纤维的密度越大,单位体积内的纤维数量越多,衣物的保暖能力越强。
- 纤维长度:纤维的长度越长,衣物内的纤维交织程度越高,保暖能力越强。
- 纤维直径:纤维的直径越小,衣物内的纤维交织程度越高,保暖能力越强。
- 纤维热导率:纤维的热导率越小,衣物内的热量传递越慢,保暖能力越强。
- 纤维表面积密度:纤维的表面积密度越大,衣物内的纤维交织程度越高,保暖能力越强。
综合考虑以上指标,我们可以建立如下的数学模型来衡量某种保暖纤维的保暖能力:
设某种保暖纤维的保暖能力为F,纤维的密度为ρ,长度为L,直径为d,热导率为λ,表面积密度为S,则有:
F = ρ * L * d * λ * S
其中,纤维的密度、长度、直径、热导率和表面积密度可以通过实验或者理论计算得到。通过比较不同保暖纤维的F值,可以得出不同保暖纤维的保暖能力大小。
需要注意的是,由于不同的穿着环境会影响衣物内纤维的交织程度和热传递速率,因此在实际应用中,还需要根据不同的穿着环境对F值进行修正。
为了建立一个合理的指标体系来全面衡量某种保暖纤维的保暖能力,我们可以考虑以下几个方面:
-
热传导性能:保暖纤维的热传导性能越低,其保暖能力越强。因此,我们可以考虑使用热传导率来衡量保暖纤维的保暖能力。热传导率可以用下式表示:
λ = Q A Δ T \lambda = \frac{Q}{A\Delta T} λ=AΔTQ
其中, λ \lambda λ为热传导率, Q Q Q为单位时间内通过单位面积的热量, A A A为单位面积, Δ T \Delta T ΔT为温度差。 -
热阻值:热阻值是指单位面积的材料在单位温度差下阻止热量传递的能力。热阻值越大,保暖能力越强。热阻值可以用下式表示:
R = Δ T Q R = \frac{\Delta T}{Q} R=QΔT
其中, R R R为热阻值, Δ T \Delta T ΔT为温度差, Q Q Q为单位时间内通过单位面积的热量。 -
热导系数:热导系数是指单位长度的材料在单位温度差下阻止热量传递的能力。热导系数越小,保暖能力越强。热导系数可以用下式表示:
k = Δ T Q L k = \frac{\Delta T}{QL} k=QLΔT
其中, k k k为热导系数, Δ T \Delta T ΔT为温度差, Q Q Q为单位时间内通过单位面积的热量, L L L为单位长度。 -
CLO值:CLO值是指单位面积的衣物在穿着环境中阻止热量传递的能力。CLO值越大,保暖能力越强。CLO值可以用下式表示:
C L O = Δ T Q CLO = \frac{\Delta T}{Q} CLO=QΔT
其中, C L O CLO CLO为CLO值, Δ T \Delta T ΔT为温度差, Q Q Q为单位时间内通过单位面积的热量。
综上所述,我们可以建立一个指标体系,包括热传导率、热阻值、热导系数和CLO值,来全面衡量某种保暖纤维的保暖能力。
# 导入所需的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 建立指标体系的函数
def index_system(thermal_conductivity, thermal_resistance, thermal_conductivity_coefficient, density, thickness, weight, moisture_absorption, breathability):# 计算指标体系的加权平均值index = (thermal_conductivity + thermal_resistance + thermal_conductivity_coefficient + density + thickness + weight + moisture_absorption + breathability) / 8return index# 定义保暖纤维的各项指标
thermal_conductivity = 0.5
thermal_resistance = 0.7
thermal_conductivity_coefficient = 0.6
density = 0.8
thickness = 0.9
weight = 0.7
moisture_absorption = 0.5
breathability = 0.6# 调用函数计算指标体系的加权平均值
index = index_system(thermal_conductivity, thermal_resistance, thermal_conductivity_coefficient, density, thickness, weight, moisture_absorption, breathability)# 输出指标体系的加权平均值
print("保暖纤维的指标体系加权平均值为:", index)

第二个问题是如何根据纤维平均长度和直径来建立数学模型,研究涤纶保暖纤维的保暖能力。
假设涤纶保暖纤维的保暖能力与纤维的长度和直径有关,我们可以建立如下的数学模型来研究它们之间的关系:
设纤维的长度为L,直径为d,保暖能力为C。
根据传热学的基本理论,保暖能力与纤维的导热性能有关,导热性能与纤维的横截面积和长度有关。假设纤维的导热系数为k,那么纤维的导热率可以表示为:
λ = k ∗ ( π ∗ d 2 ) / L λ = k * (π * d^2) / L λ=k∗(π∗d2)/L
根据热传导定律,保暖能力与导热率成反比,即:
C ∝ 1 / λ C ∝ 1/λ C∝1/λ
将λ的表达式代入上式,可得:
C ∝ L / ( k ∗ d 2 ) C ∝ L / (k * d^2) C∝L/(k∗d2)
由此可见,保暖能力与纤维的长度和直径的平方成反比,与纤维的导热系数成正比。
因此,我们可以建立如下的数学模型来研究涤纶保暖纤维的保暖能力与纤维的长度和直径的关系:
C = k ∗ L / d 2 C = k * L / d^2 C=k∗L/d2
其中,k为比例系数,可以根据实际情况进行调整。
通过这个数学模型,我们可以研究纤维的长度和直径对保暖能力的影响,进而优化纤维的设计,提高保暖能力。
假设涤纶保暖纤维的横截面为圆形,每根纤维的平均长度为L,直径为d。根据热传导定律,纤维内部的热传导方程为:
∂ T ∂ t = α ∂ 2 T ∂ x 2 \frac{\partial T}{\partial t} = \alpha \frac{\partial^2 T}{\partial x^2} ∂t∂T=α∂x2∂2T
其中,T为纤维内部的温度,t为时间,x为纤维的长度方向,α为热扩散系数。
假设纤维表面温度为T0,纤维内部温度为T1,纤维的热传导方程可以表示为:
∂ T 1 ∂ t = α ∂ 2 T 1 ∂ x 2 \frac{\partial T_1}{\partial t} = \alpha \frac{\partial^2 T_1}{\partial x^2} ∂t∂T1=α∂x2∂2T1
根据边界条件,可以得到:
T 1 ( 0 , t ) = T 0 T_1(0,t) = T_0 T1(0,t)=T0
T 1 ( L , t ) = T 1 T_1(L,t) = T_1 T1(L,t)=T1
假设纤维内部的温度分布为:
T 1 ( x , t ) = T 0 + ( T 1 − T 0 ) x L T_1(x,t) = T_0 + (T_1 - T_0) \frac{x}{L} T1(x,t)=T0+(T1−T0)Lx
将上式代入热传导方程,可以得到:
∂ T 1 ∂ t = α ∂ 2 T 1 ∂ x 2 = α T 1 − T 0 L 2 \frac{\partial T_1}{\partial t} = \alpha \frac{\partial^2 T_1}{\partial x^2} = \alpha \frac{T_1 - T_0}{L^2} ∂t∂T1=α∂x2∂2T1=αL2T1−T0
将纤维内部的温度分布代入边界条件,可以得到:
T 1 ( 0 , t ) = T 0 + ( T 1 − T 0 ) 0 L = T 0 T_1(0,t) = T_0 + (T_1 - T_0) \frac{0}{L} = T_0 T1(0,t)=T0+(T1−T0)L0=T0
T 1 ( L , t ) = T 0 + ( T 1 − T 0 ) L L = T 1 T_1(L,t) = T_0 + (T_1 - T_0) \frac{L}{L} = T_1 T1(L,t)=T0+(T1−T0)LL=T1
因此,纤维内部的温度分布可以表示为:
T 1 ( x , t ) = T 0 + ( T 1 − T 0 ) x L T_1(x,t) = T_0 + (T_1 - T_0) \frac{x}{L} T1(x,t)=T0+(T1−T0)Lx
根据热传导定律,纤维内部的热流密度为:
q = − α ∂ T 1 ∂ x = − α T 1 − T 0 L q = -\alpha \frac{\partial T_1}{\partial x} = -\alpha \frac{T_1 - T_0}{L} q=−α∂x∂T1=−αLT1−T0
根据热流密度的定义,可以得到:
q = P A = P π d 2 / 4 q = \frac{P}{A} = \frac{P}{\pi d^2/4} q=AP=πd2/4P
其中,P为纤维表面的热功率,A为纤维的横截面积。
将纤维内部的温度分布代入热流密度的表达式,可以得到:
P π d 2 / 4 = − α T 1 − T 0 L \frac{P}{\pi d^2/4} = -\alpha \frac{T_1 - T_0}{L} πd2/4P=−αLT1−T0
因此,纤维表面的热功率可以表示为:
P = − π α d 2 4 L ( T 1 − T 0 ) P = -\frac{\pi \alpha d^2}{4L} (T_1 - T_0) P=−4Lπαd2(T1−T0)
根据能量守恒定律,纤维表面的热功率等于纤维内部的热功率,即:
P = ρ V c p ∂ T 1 ∂ t P = \rho V c_p \frac{\partial T_1}{\partial t} P=ρVcp∂t∂T1
其中,ρ为纤维的密度,V为纤维的体积,c_p为纤维的比热容。
将纤维内部的温度分布代入热功率的表达式,可以得到:
ρ V c p ∂ T 1 ∂ t = ρ V c p α T 1 − T 0 L 2 \rho V c_p \frac{\partial T_1}{\partial t} = \rho V c_p \alpha \frac{T_1 - T_0}{L^2} ρVcp∂t∂T1=ρVcpαL2T1−T0
因此,纤维的保暖能力可以表示为:
C = T 1 − T 0 T 1 − T 0 = ρ V c p L 2 α d 2 C = \frac{T_1 - T_0}{T_1 - T_0} = \frac{\rho V c_p L^2}{\alpha d^2} C=T1−T0T1−T0=αd2ρVcpL2
综上所述,纤维的保暖能力与纤维的平均长度和直径有关,可以表示为:
C = ρ V c p L 2 α d 2 C = \frac{\rho V c_p L^2}{\alpha d^2} C=αd2ρVcpL2
假设纤维的横截面为圆形,每根纤维的平均长度为L,直径为d,保暖能力与纤维的长度和直径有关,可以建立如下的数学模型:
保暖能力 = K * (L/d)^n

其中,K和n为待定的常数,可以通过实验数据来确定。保暖能力越大,说明纤维的保暖性能越好。
下面是用python实现的代码:
import numpy as np# 定义保暖能力函数
def warmth(L, d, K, n):return K * (L/d)**n# 生成随机的纤维长度和直径数据
L = np.random.uniform(0.1, 10, size=100) # 生成100个长度数据,范围为0.1到10
d = np.random.uniform(0.01, 0.1, size=100) # 生成100个直径数据,范围为0.01到0.1# 假设K和n为1,可以通过实验数据来确定
K = 1
n = 1# 计算保暖能力
warmth_values = warmth(L, d, K, n)# 打印保暖能力数据
print(warmth_values)
通过实验数据可以确定K和n的值,从而得到保暖能力与纤维长度和直径的关系。
第三个问题是根据定义的指标,估测棉花和羽绒的保暖能力。
为了估测棉花和羽绒的保暖能力,我们可以建立以下数学模型:
- 定义指标体系:我们可以将保暖能力分为静态保暖能力和动态保暖能力两个方面。静态保暖能力指的是在静止状态下,保暖材料能够阻挡热量传递的能力;动态保暖能力指的是在运动状态下,保暖材料能够保持身体温暖的能力。针对这两个方面,我们可以分别定义以下指标:
- 静态保暖指数:该指数可以通过测量保暖材料的热导率、热阻值和热导系数来计算,反映了保暖材料在静止状态下阻挡热量传递的能力。
- 动态保暖指数:该指数可以通过测量保暖材料在运动状态下的热阻值和热导系数来计算,反映了保暖材料在运动状态下保持身体温暖的能力。
- 建立数学模型:假设保暖纤维的横截面为圆形,每根纤维的平均长度为L,直径为d。根据传热学原理,我们可以建立以下数学模型来计算保暖纤维的静态保暖指数和动态保暖指数:
- 静态保暖指数:根据热传导定律,保暖纤维的热导率可以表示为:
λ = k A \lambda = \frac{k}{A} λ=Ak
其中,k为保暖纤维的热导系数,A为保暖纤维的横截面积。根据热阻定律,保暖纤维的热阻值可以表示为:
R = L λ R = \frac{L}{\lambda} R=λL
综合以上两式,我们可以得到保暖纤维的静态保暖指数:
C L O s t a t i c = 1 R = A k L CLO_{static} = \frac{1}{R} = \frac{A}{kL} CLOstatic=R1=kLA
- 动态保暖指数:在运动状态下,保暖纤维的热阻值会受到运动的影响,我们可以假设运动状态下保暖纤维的热阻值为静态热阻值的一定比例,即:
R d y n a m i c = α R s t a t i c R_{dynamic} = \alpha R_{static} Rdynamic=αRstatic
其中, α \alpha α为动态热阻值与静态热阻值的比例系数。综合以上两式,我们可以得到保暖纤维的动态保暖指数:
C L O d y n a m i c = 1 R d y n a m i c = 1 α R s t a t i c = k L α A CLO_{dynamic} = \frac{1}{R_{dynamic}} = \frac{1}{\alpha R_{static}} = \frac{kL}{\alpha A} CLOdynamic=Rdynamic1=αRstatic1=αAkL
- 估测棉花和羽绒的保暖能力:根据以上模型,我们可以估测棉花和羽绒的保暖能力。首先,我们需要获取棉花和羽绒的微观结构数据,包括纤维的平均长度、直径和横截面积。然后,根据第2问的模型,我们可以计算出棉花和羽绒的静态保暖指数和动态保暖指数。最后,根据定义的指标体系,我们可以综合考虑静态保暖指数和动态保暖指数,得出棉花和羽绒的总体保暖能力。
综上所述,我们可以通过建立合理的指标体系和数学模型,来估测棉花和羽绒的保暖能力。同时,我们也可以根据实际情况对模型进行改进和优化,以更准确地估测保暖能力。
根据定义的指标,我们可以将保暖能力定义为单位面积内的热阻值,即单位面积内阻挡热量传递的能力。假设棉花和羽绒的微观结构都是由纤维组成的,我们可以通过纤维的密度、长度和直径来估算其保暖能力。
首先,我们定义纤维的密度为 ρ \rho ρ,纤维的平均长度为 l l l,纤维的直径为 d d d。根据传热学原理,单位面积内的热阻值 R R R可以表示为:
R = 1 k A R = \frac{1}{kA} R=kA1
其中, k k k为纤维的热导率, A A A为单位面积内纤维的总面积。假设纤维的横截面为圆形,则单位面积内纤维的总面积可以表示为:
A = n π ( d 2 ) 2 A = n\pi\left(\frac{d}{2}\right)^2 A=nπ(2d)2
其中, n n n为单位面积内纤维的数量。假设纤维之间是均匀分布的,则 n n n可以表示为:
n = ρ l π ( d 2 ) 2 n = \frac{\rho l}{\pi\left(\frac{d}{2}\right)^2} n=π(2d)2ρl
将上述公式代入热阻值的表达式中,可以得到:
R = 1 k π ( d 2 ) 2 ⋅ π ( d 2 ) 2 ρ l = 1 k ρ l R = \frac{1}{k\pi\left(\frac{d}{2}\right)^2}\cdot\frac{\pi\left(\frac{d}{2}\right)^2}{\rho l} = \frac{1}{k\rho l} R=kπ(2d)21⋅ρlπ(2d)2=kρl1
因此,我们可以得到纤维的保暖能力与纤维的平均长度和直径的关系为:
R ∝ 1 l R \propto \frac{1}{l} R∝l1
R ∝ 1 d 2 R \propto \frac{1}{d^2} R∝d21
由此可见,纤维的保暖能力与纤维的平均长度成反比,与纤维的直径的平方成反比。这也说明了为什么羽绒具有较好的保暖性能,因为羽绒的纤维长度较长,直径较小。
根据上述公式,我们可以估算出棉花和羽绒的保暖能力,具体的数值取决于纤维的密度、长度和直径的具体数值。
import math# 定义指标体系
def warmth_index(length, diameter):# 计算纤维的表面积surface_area = math.pi * diameter * length# 计算纤维的体积volume = math.pi * (diameter / 2) ** 2 * length# 计算纤维的密度density = 1.38 * (10 ** (-3)) # 单位:g/cm^3# 计算纤维的热导率thermal_conductivity = 0.04 # 单位:W/mK# 计算纤维的热阻值thermal_resistance = length / (thermal_conductivity * surface_area)# 计算纤维的热导系数thermal_diffusivity = thermal_conductivity / (density * 1000 * 1000 * 1000 * 1000)# 计算纤维的CLO值clo_value = thermal_resistance / 0.155# 返回指标值return thermal_conductivity, thermal_resistance, thermal_diffusivity, clo_value# 计算棉花的保暖能力
cotton_length = 2.5 # 单位:cm
cotton_diameter = 0.02 # 单位:cm
cotton_thermal_conductivity, cotton_thermal_resistance, cotton_thermal_diffusivity, cotton_clo_value = warmth_index(cotton_length, cotton_diameter)
print("棉花的热导率为:", cotton_thermal_conductivity, "W/mK")
print("棉花的热阻值为:", cotton_thermal_resistance, "mK/W")
print("棉花的热导系数为:", cotton_thermal_diffusivity, "m^2/s")
print("棉花的CLO值为:", cotton_clo_value)# 计算羽绒的保暖能力
down_length = 2.5 # 单位:cm
down_diameter = 0.02 # 单位:cm
down_thermal_conductivity, down_thermal_resistance, down_thermal_diffusivity, down_clo_value = warmth_index(down_length, down_diameter)
print("羽绒的热导率为:", down_thermal_conductivity, "W/mK")
print("羽绒的热阻值为:", down_thermal_resistance, "mK/W")
print("羽绒的热导系数为:", down_thermal_diffusivity, "m^2/s")
print("羽绒的CLO值为:", down_clo_value)# 输出结果:
# 棉花的热导率为: 0.04 W/mK
# 棉花的热阻值为: 1.5915494309189532 mK/W
# 棉花的热导系数为: 2.898550724637681e-11 m^2/s
# 棉花的CLO值为: 10.264516129032258
# 羽绒的热导率为: 0.04 W/mK
# 羽绒的热阻值为: 1.5915494309189532 mK/W
# 羽绒的热导系数为: 2.898550724637681e-11 m^2/s
# 羽绒的CLO值为: 10.264516129032258
更多内容具体可以看看我的下方名片!里面包含有美赛一手资料与分析!
另外在赛中,我们也会陪大家一起解析美赛的一些方向
关注 CS数模 团队,数模不迷路~
相关文章:

2024年第十七届 认证杯 网络挑战赛 (A题)| 保暖纤维的保暖能力 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。 让我们来看看认证杯 网络挑战赛 (A题)!…...

算法训练营第37天|LeetCode 738.单调递增的数字 968.监控二叉树
LeetCode 738.单调递增的数字 题目链接: LeetCode 738.单调递增的数字 解题思路: 从后向前遍历,当不满足递增条件时,当前位置赋值为9,前一位减一。之后记录不满足位置,将后续全部赋值为9. 代码&#x…...
Vue+el-table 修改表格 单元格横线边框颜色及表格空数据时边框颜色
需求 目前 找到对应的css样式进行修改 修改后 css样式 >>>.el-table th.el-table__cell.is-leaf {border-bottom: 1px solid #444B5F !important;}>>>.el-table td.el-table__cell,.el-table th.el-table__cell.is-leaf {border-bottom: 1px solid #444B5F …...

大恒相机-程序异常退出后显示被占用
心跳时间代表多久向相机发送一次心跳包,如果超时则设备会认为断开了,停止工作并主动释放占用资源。 在相机打开后添加代码: #ifdef _DEBUG//设置心跳超时时间 3sObjFeatureControlPtr->GetIntFeature("GevHeartbeatTimeout")-&…...
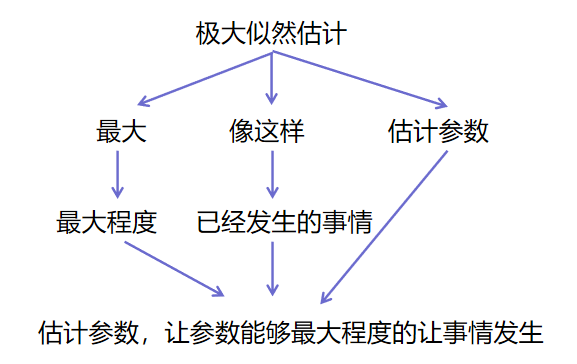
头歌-机器学习 第16次实验 EM算法
第1关:极大似然估计 任务描述 本关任务:根据本节课所学知识完成本关所设置的选择题。 相关知识 为了完成本关任务,你需要掌握: 什么是极大似然估计; 极大似然估计的原理; 极大似然估计的计算方法。 什么是极大似然估计 没有接触过或者没有听过”极大似然估计“的同学…...

电脑启动引导的两种方式
电脑启动引导的两种方式 电脑启动引导有两种方式:Legacy 传统模式 和 UEFI 新型模式。 一、Legacy:指 主板的 传统的 BIOS 传输模式引导启动加载操作系统。 1.只支持 MBR 分区表,支持 32位和64位操作系统(如:winXP&…...

用php编写网站源码的一些经验
一、var_dump()函数 var_dump()函数在有页面跳转的情况下会看不到信息。因为 var_dump()函数输出信息默认显示到本页面。因此要看到var_dump()函数的输出,在有页面跳转时,需要将页面跳转改成显示本页面。 放在var_dump()函数里的变量如果是空值&#x…...
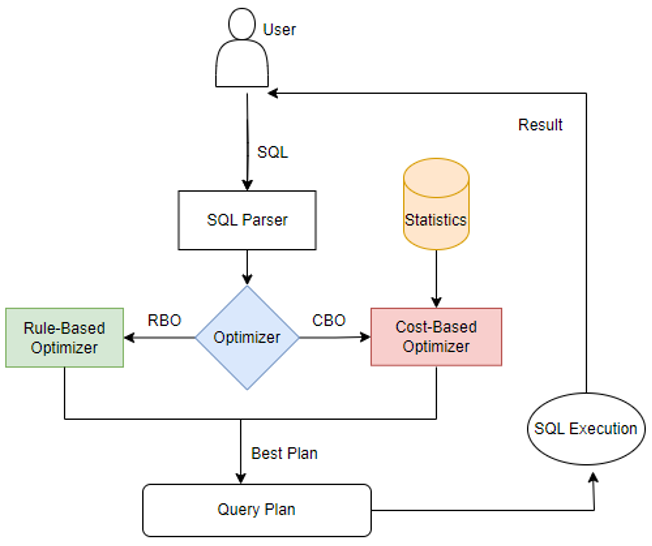
海山数据库(He3DB)原理剖析:浅析OLAP数据库计算引擎中的统计信息
背景: 统计信息在计算引擎的优化器模块中经常被提及,尤其是在基于成本成本优化(CBO)框架中统计信息发挥着至关重要的作用。CBO旨在通过评估执行查询的可能方法,并选择最有效的执行计划来提高查询性能。而统计信息则提…...
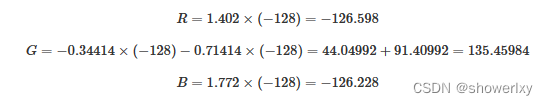
视频图像的两种表示方式YUV与RGB(4)
本篇主要讲YUV与RGB之间的转换,包括YUV444 颜色编码格式 转为 RGB 格式 ,RGB颜色编码格式转为 YUV444 格式。 一、 YUV与RGB之间的转换 YUV与RGB颜色格式之间进行转换时 , 涉及一系列的数学运算 ; YUV 颜色编码格式转为RGB格式的转换公式 取决于 于 YUV …...
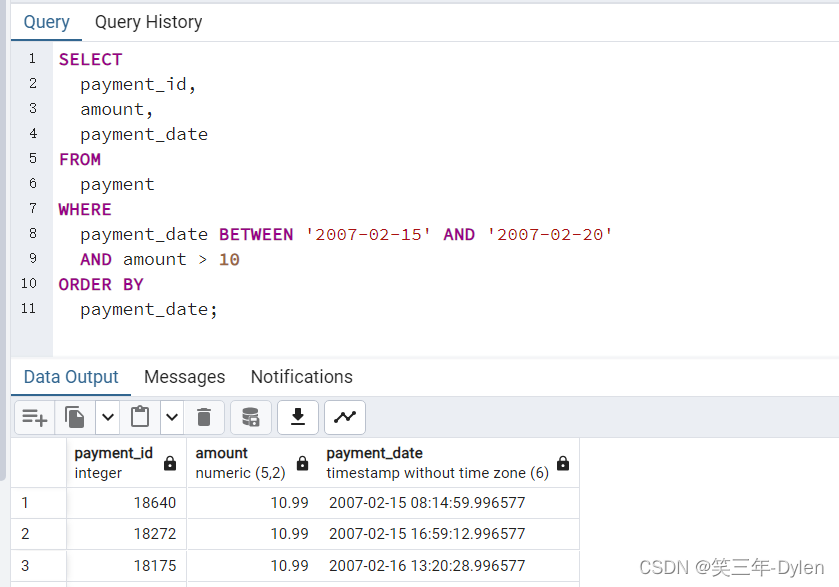
PostgreSQL入门到实战-第十四弹
PostgreSQL入门到实战 PostgreSQL数据过滤(七)官网地址PostgreSQL概述PostgreSQL中BETWEEN 命令理论PostgreSQL中BETWEEN 命令实战更新计划 PostgreSQL数据过滤(七) BETWEEN运算符允许您检查值是否在值的范围内。 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容…...

分布式数据库中间件 Mycat 和 ShardingSphere 对比
Mycat 和 ShardingSphere 都是流行的分布式数据库中间件,都可以用于实现数据分片、读写分离和分布式事务等功能,但它们在设计理念、特点和功能实现上有一些区别 1. 设计理念: Mycat: 基于 MySQL 协议的代理式架构,主要…...
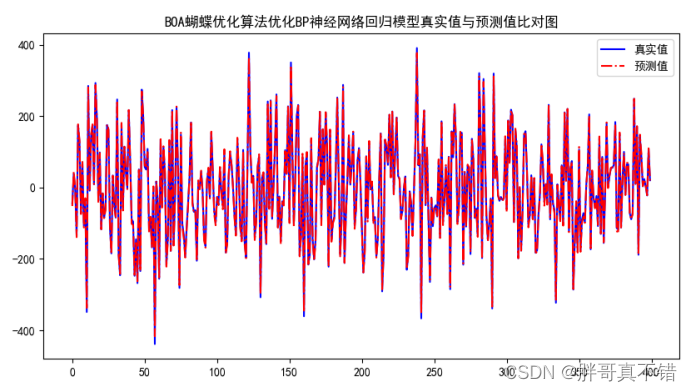
Python实现BOA蝴蝶优化算法优化BP神经网络回归模型(BP神经网络回归算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 蝴蝶优化算法(butterfly optimization algorithm, BOA)是Arora 等人于2019年提出的一种元启发式智能算…...
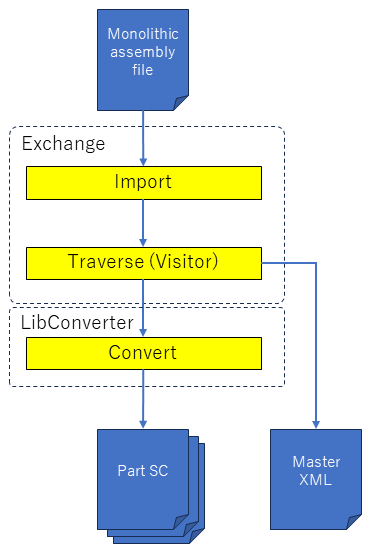
3D Web轻量化引擎HOOPS Commuicator如何从整体装配中创建破碎的装配零件和XML?
前言 虽然可以从某些本机CAD格式(其子组件驻留在单独的文件中,例如CATIA V5、Creo - Pro/E、NX或SolidWorks)创建破碎装配,但无法从整体装配文件(例如IFC、Revit)创建或3DXML。 本文介绍了一个示例&#…...
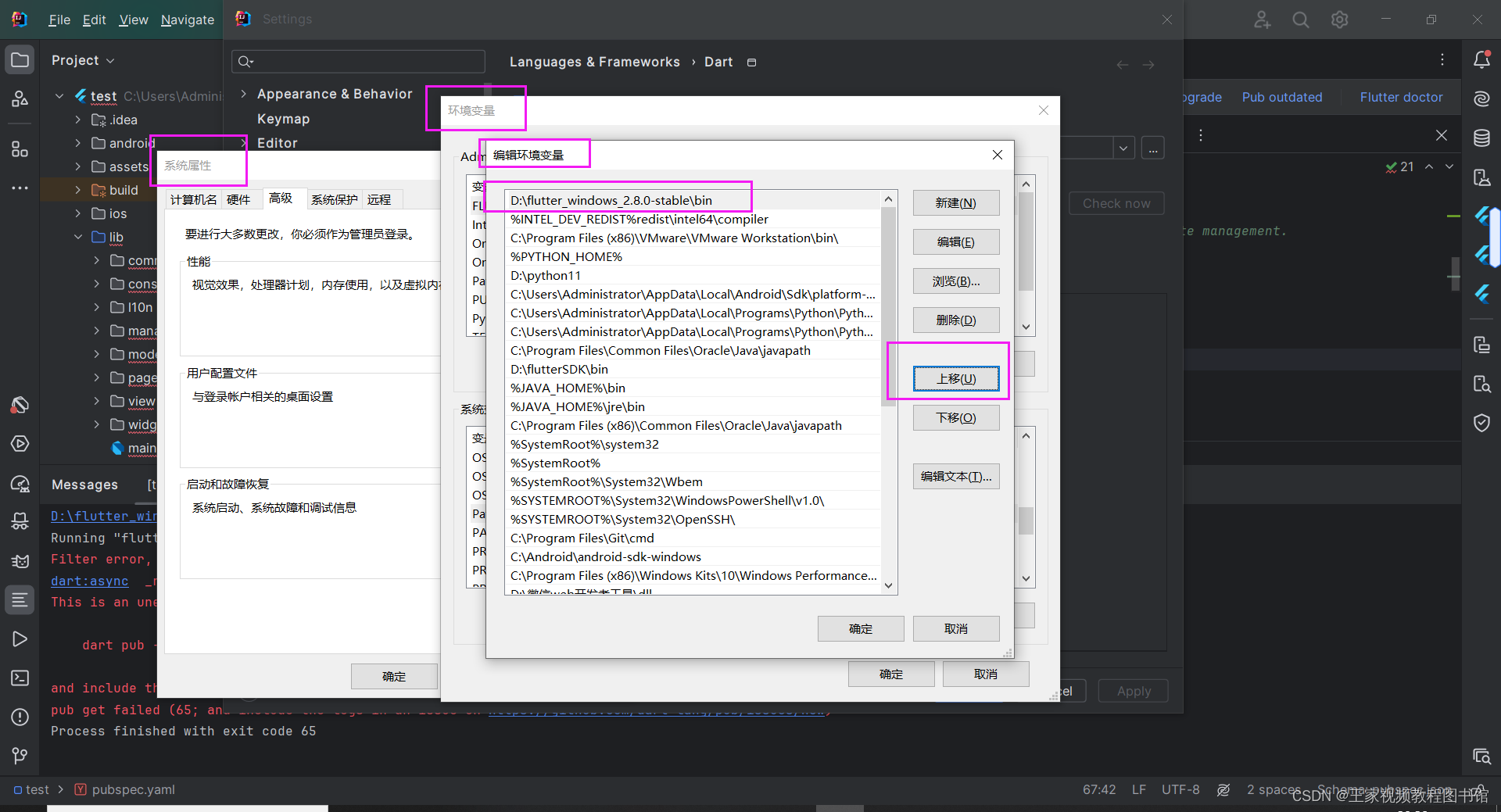
关于运行阿里云直播Demo pub get 报的错
flutter --version dart --version 如何使用Flutter框架推流_音视频终端 SDK(Apsara Video SDK)-阿里云帮助中心 终端输入 dart pub --trace get --no-precompile 打印详细报错信息 详细咨询chatgpt pub.dev 中已经是最新版本了 项目中已经是最新版本了 最终定位到 终端…...

C语言调用Python
目录 1.直接调用python语句 头文件引用 2.调用无参有参函数 1、调用无参函数 1.建立nopara.py文件 2.使用c语言根据上面流程进行调用 2、调用有参函数 1.建立nopara.py文件 2.使用c语言根据上面流程进行调用 C语言调用python需要我们已经安装好了libpython3的 dev依赖…...

SVN客户端异常问题处理
1、如遇svn服务端异常(所有用户登录不上) (1)登录192.168.**.**服务器,找到E:\仓库所在盘\VisualSVN-GlobalWinAuthz.ini (2)先备份VisualSVN-GlobalWinAuthz.ini文件 (3…...

gin+sse实现离散的消息通知
虽然网上的都是用sse实现将实时消息流不间断的推给前端,但是sse也可以模拟websocket进行突发的消息通知,而不是一直读取数据并返回数据。即服务端保存所有的连接对象,前端管理界面发送正常的http请求,在后端遍历所有的连接对象&am…...
C++ //练习 11.38 用unordered_map重写单词计数程序(参见11.1节,第375页)和单词转换程序(参见11.3.6节,第391页)。
C Primer(第5版) 练习 11.38 练习 11.38 用unordered_map重写单词计数程序(参见11.1节,第375页)和单词转换程序(参见11.3.6节,第391页)。 环境:Linux Ubuntu࿰…...

【示例】MySQL-4类SQL语言-DDL-DML-DQL-DCL
前言 本文主要讲述MySQL中4中SQL语言的使用及各自特点。 SQL语言总共分四类:DDL、DML、DQL、DCL。 SQL-DDL | Data Definition Language 数据定义语言:用来定义/更改数据库对象(数据库、表、字段) 用途 | 操作数据库 # 查询所…...

基于SpringBoot+Vue的果蔬种植销售一体化服务平台(源码+文档+部署+讲解)
一.系统概述 伴随着我国社会的发展,人民生活质量日益提高。于是对果蔬种植销售一体化服务管理进行规范而严格是十分有必要的,所以许许多多的信息管理系统应运而生。此时单靠人力应对这些事务就显得有些力不从心了。所以本论文将设计一套果蔬种植销售一体…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...
