【数据结构】考研真题攻克与重点知识点剖析 - 第 8 篇:排序
前言
- 本文基础知识部分来自于b站:分享笔记的好人儿的思维导图与王道考研课程,感谢大佬的开源精神,习题来自老师划的重点以及考研真题。
- 此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析,本人技术有限,最终数据清洗结果不够理想,相关CSDN文章便没有发出。
(考研真题待更新)
欢迎订阅专栏:408直通车
请注意,本文中的部分内容来自网络搜集和个人实践,如有任何错误,请随时向我们提出批评和指正。本文仅供学习和交流使用,不涉及任何商业目的。如果因本文内容引发版权或侵权问题,请通过私信告知我们,我们将立即予以删除。
文章目录
- 前言
- 第八章 排序
- 概述
- 排序
- 算法的稳定性
- 根据数据是否在内存中进行分类
- 小结
- 插入排序
- 直接插入排序
- 折半插入排序
- 小结
- 希尔排序
- 小结
- 交换排序
- 概述
- 冒泡排序
- 小结
- 快速排序
- 选择排序
- 概述
- 简单选择排序
- 小结
- 堆排序
- 小结
- 堆的插入删除
- 插入
- 删除
- 二路归并排序
- 实现过程
- 基数排序
- 基本概念
- 实现过程
- 性能分析
- 稳定性
- 应用
- 补充
- 排序算法的分析
- 结论
- 外部排序
- 外部排序基本概念
- 构造初始“归并段"
- 第一趟归并
- 第二趟归并
- 第三趟归并
- 外部排序的方法
- 优化(都减少归并趟数s,减少磁盘读写次数)
- 多路平衡归并与败者树
- 置换-选择排序(生成初始归并段)
- 最佳归并树(k叉哈夫曼树)
- 代码
- 快排
- 归并
- 二分查找(可用于折半)
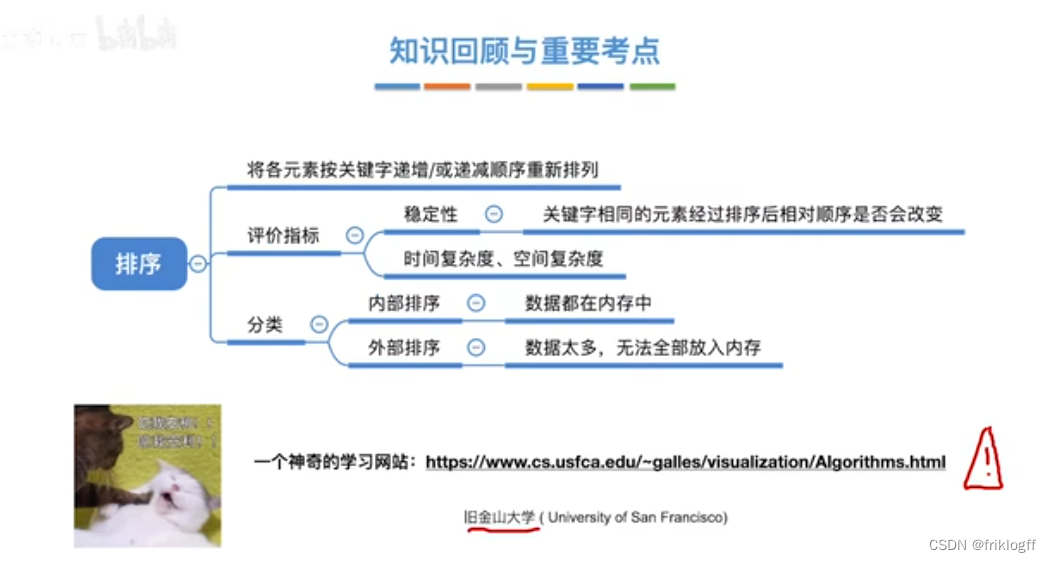
第八章 排序
概述
排序
- 将无序序列排成一个有序序列的运算(如果排序的数据结点包含多个数据域,排序针对一个域)

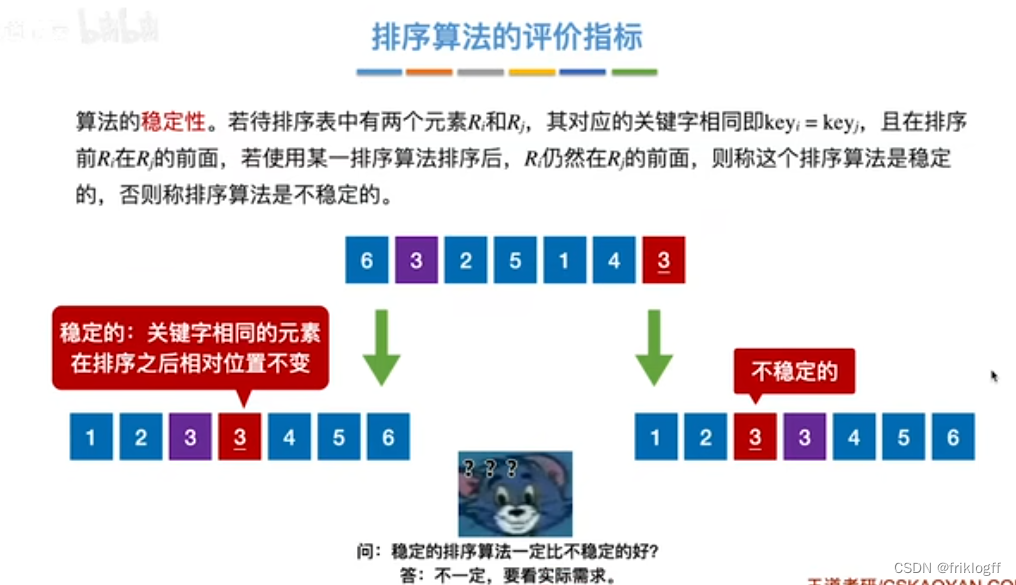
算法的稳定性
-
能够使任何数值相等的元素,排序以后相对次序不变
-
稳定性只对结构类型数据排序有意义,例:先按数学成绩排序,再按总分排序
根据数据是否在内存中进行分类
-
内部排序
- 在排序期间元素全部存放在内存中的排序
-
外部排序
- 在排序期间元素无法全部同时存放在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动的排序
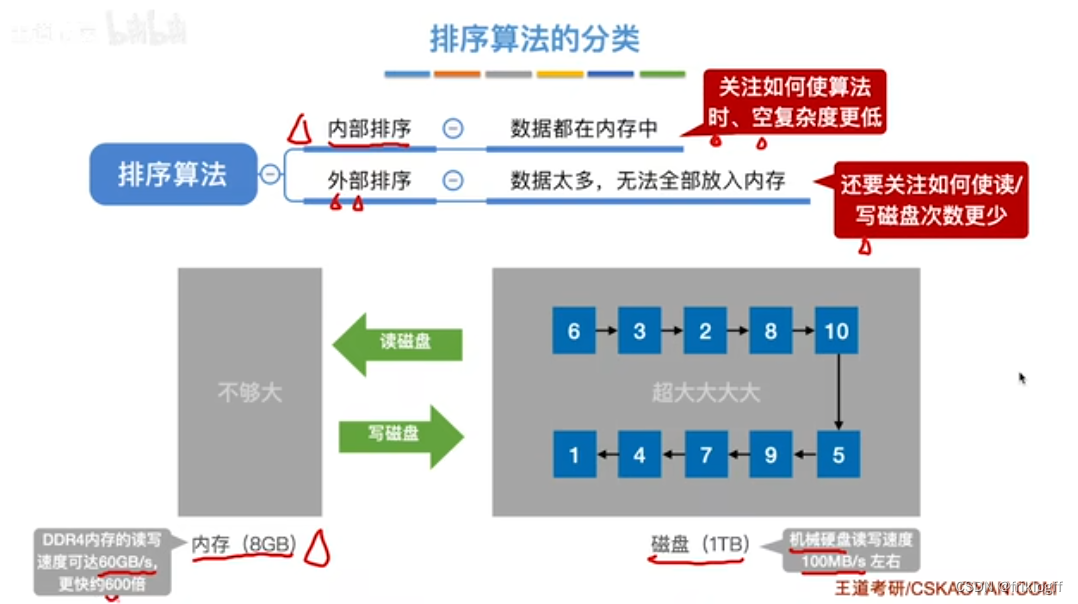
- 在排序期间元素无法全部同时存放在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动的排序
小结
插入排序
直接插入排序
-
概念
- 首先以一个元素为有序的序列,然后讲后面的元素依次插入到有序的序列中适合的位置直到所有元素都插入有序序列

- 首先以一个元素为有序的序列,然后讲后面的元素依次插入到有序的序列中适合的位置直到所有元素都插入有序序列
-
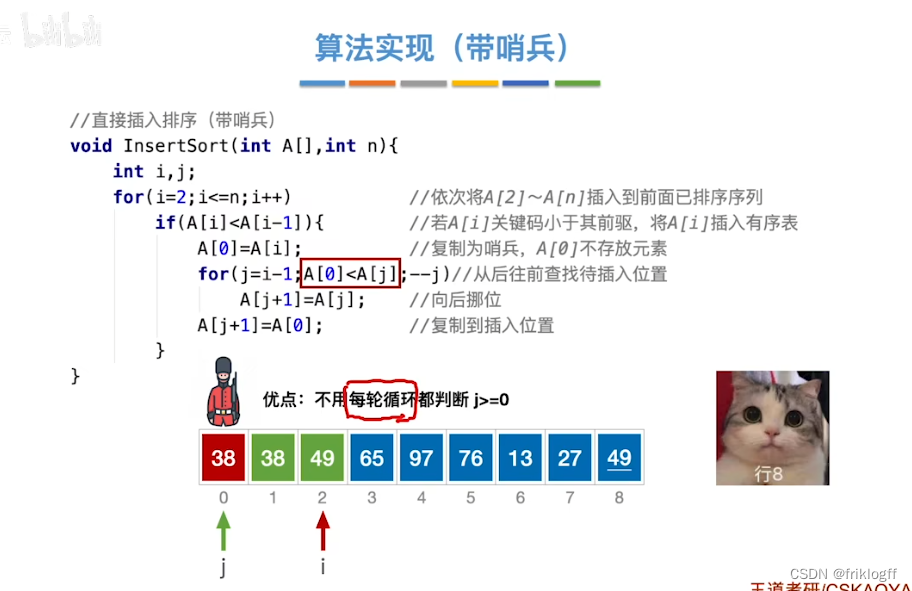
实现过程
-
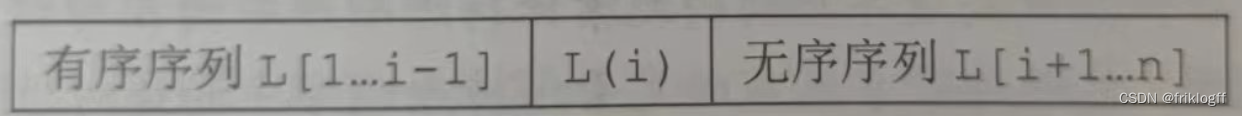
-
排序某时刻将待排序表分割为三部分,顺序查出L(i)在L[1…i-1]的插入位置k
-
将L[k…i-1]中的所有元素依次后移一个位置,将L(i)复制到L(k)
-
-
哨兵
-
-
性能分析
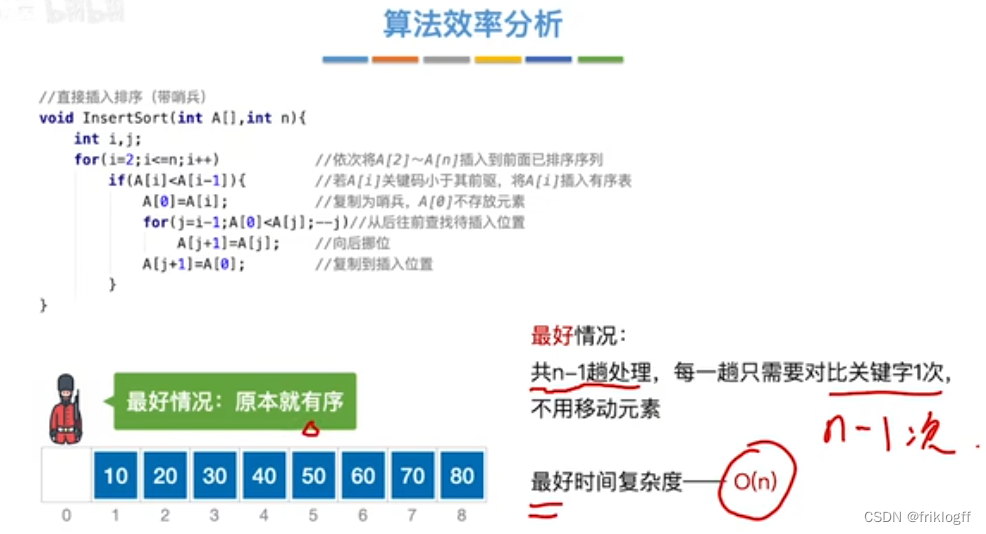


-
时间复杂度(平均):O(n^2)
-
最好(有序):O(n)
- 最坏(逆序):O(n^2)
-
-
空间复杂度:O(1)
-
-
稳定性
- 稳定
-
补充提高速度
-
减少元素比较次数,引入折半插入排序
-
减少元素的移动次数,引入希尔排序,每次移动步幅增大
-
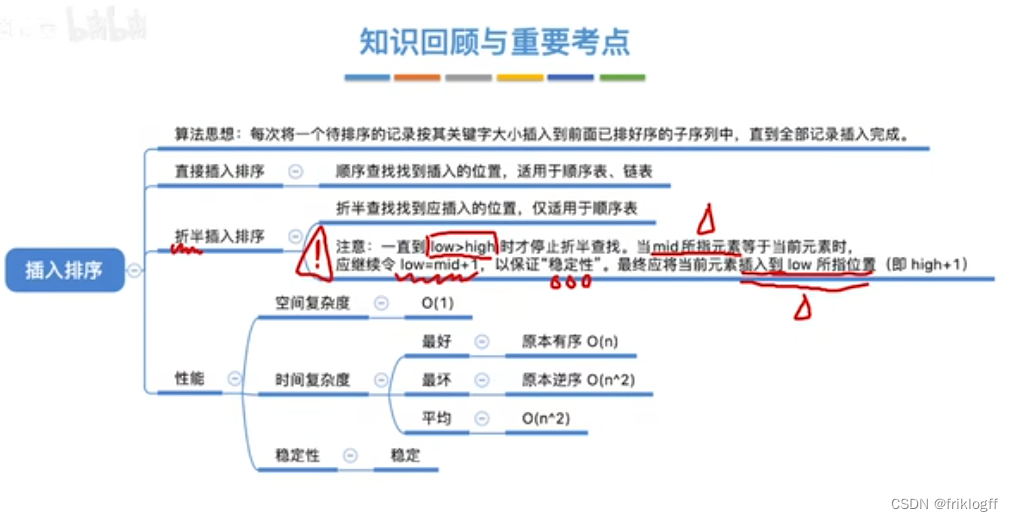
折半插入排序

-
实现过程
- 首先确定折半插入排序的范围,利用折半查找找到插入的位置,然后一次性对数据进行移动,最后插入该元素
-
性能分析
-
时间复杂度:比较次数减少O(nlogn),移动次数不变,整体O(n^2)
-
空间复杂度:O(1)
-
-
稳定性
- 稳定
小结
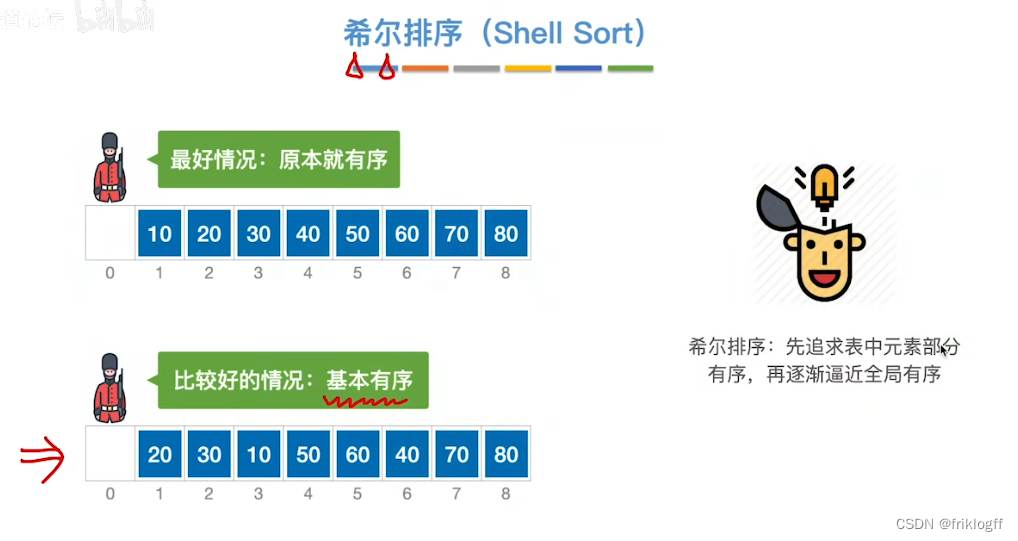
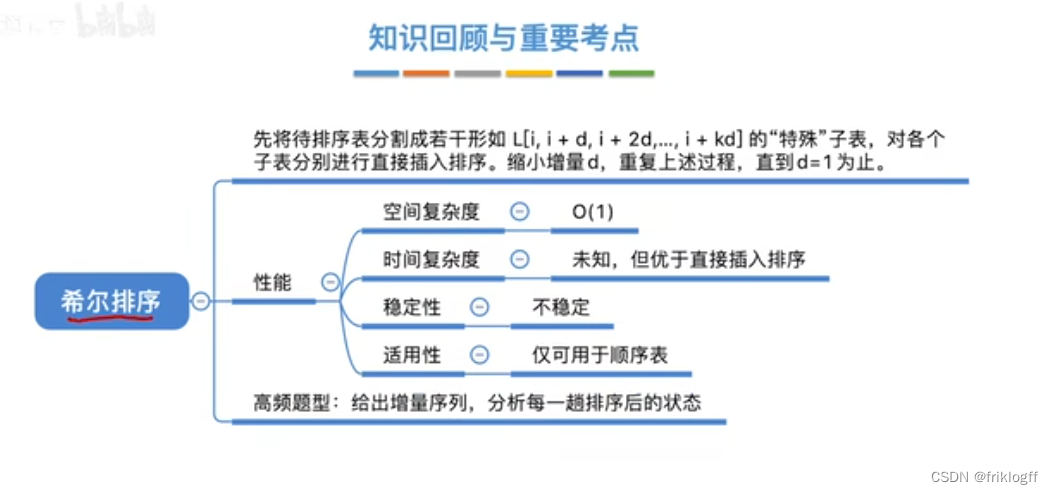
希尔排序
-
概念
- 本质上还是插入排序,只是把待排序列分成几个子序列,分别对子序列进行直接插入排序
-
实现过程
-
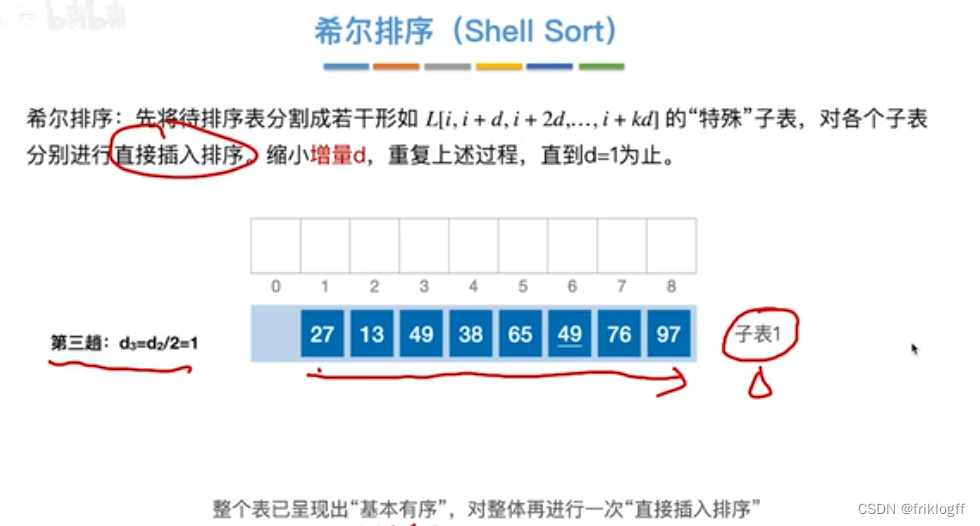
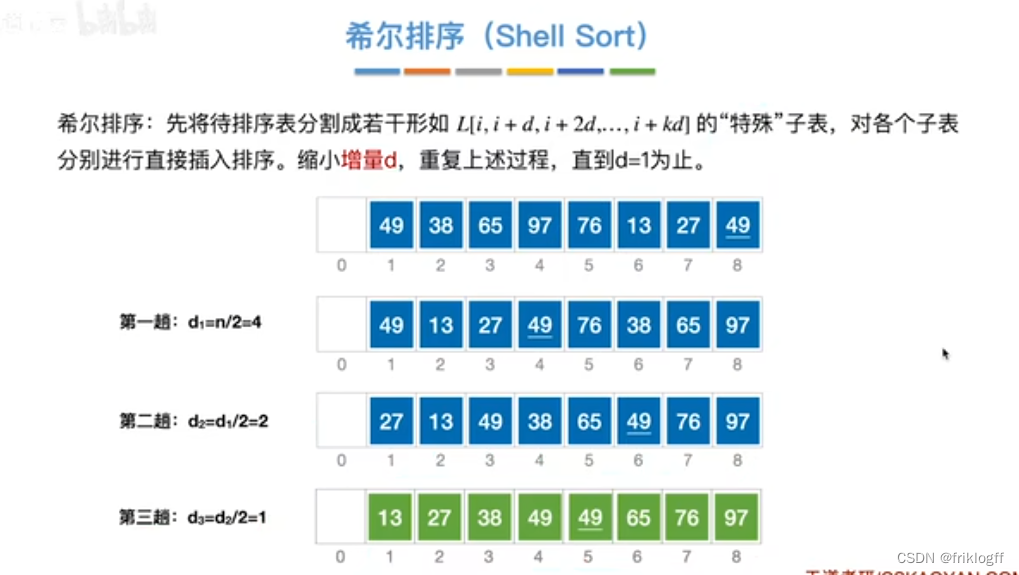
先取一个小于n的步长d,把表中数据分为d组,所有距离为d的倍数记录在同一组,组内进行直接插入排序
-
缩小步长d,不断重复直到d=1为止
-
若d=5,跨越6个数







-
-
性能分析
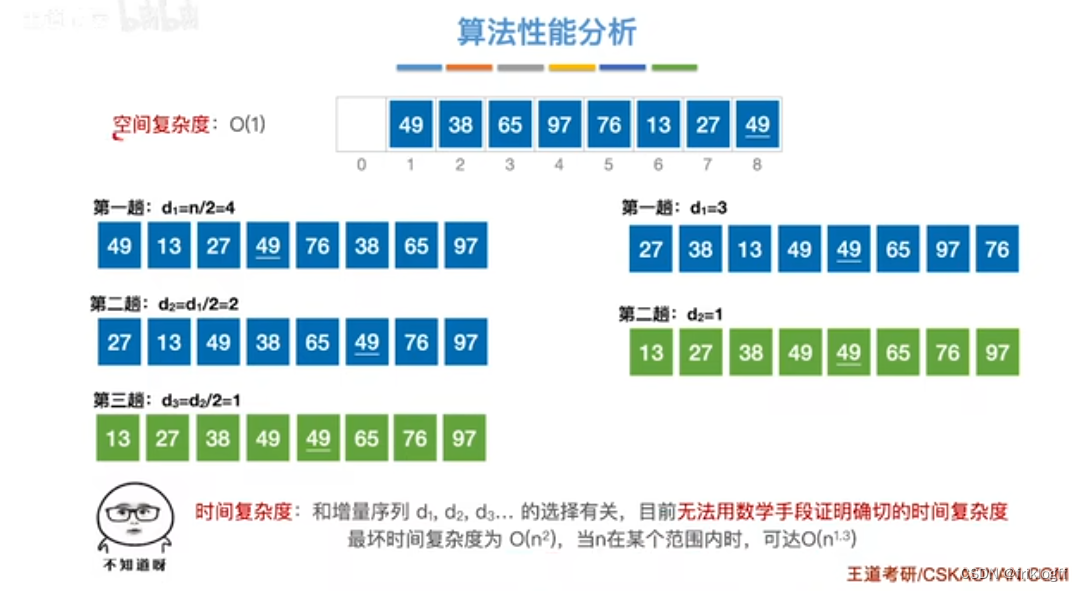
-
时间复杂度(平均):O(n^1.3)
- 最坏:O(n^2)
-
空间复杂度:O(1)
-
-
稳定性
- 不稳定
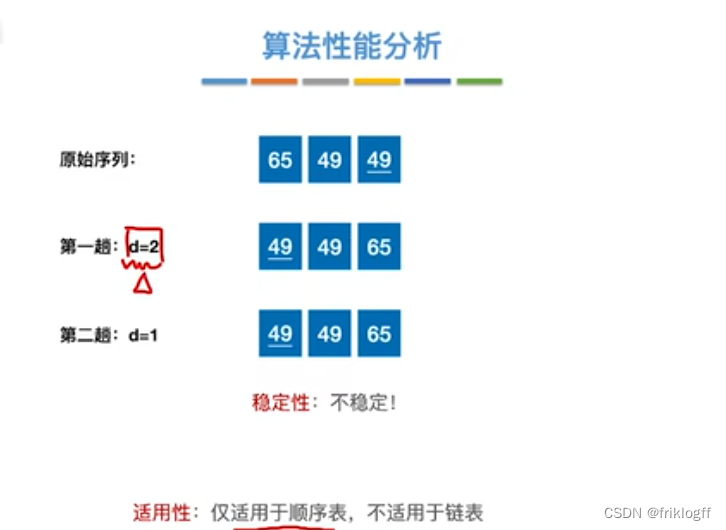
- 不稳定
小结
交换排序
概述
- 根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置
冒泡排序
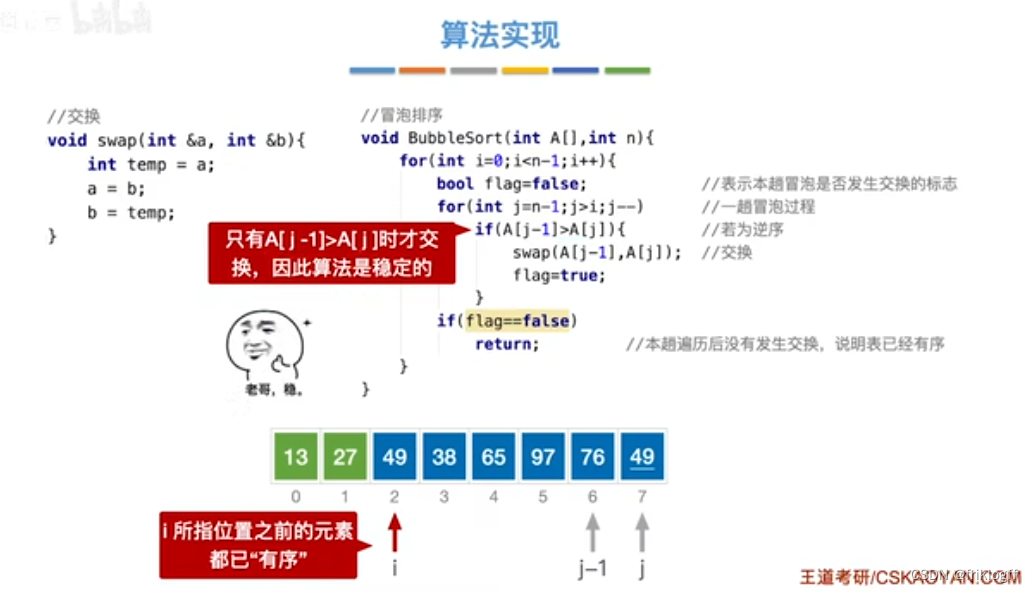
-
实现过程
-
从前往后(从后往前)两两比较相邻元素的值,若逆序则交换,直到序列比较完
-
每一趟会将最大的元素交换到待排序列最后一个位置(将较小的元素交换到待排序列第一个位置)
-
进行下一趟排序,前一趟确定元素不参与
-
如果某一趟排序过程中未发生交换,则可以提前结束
-
-
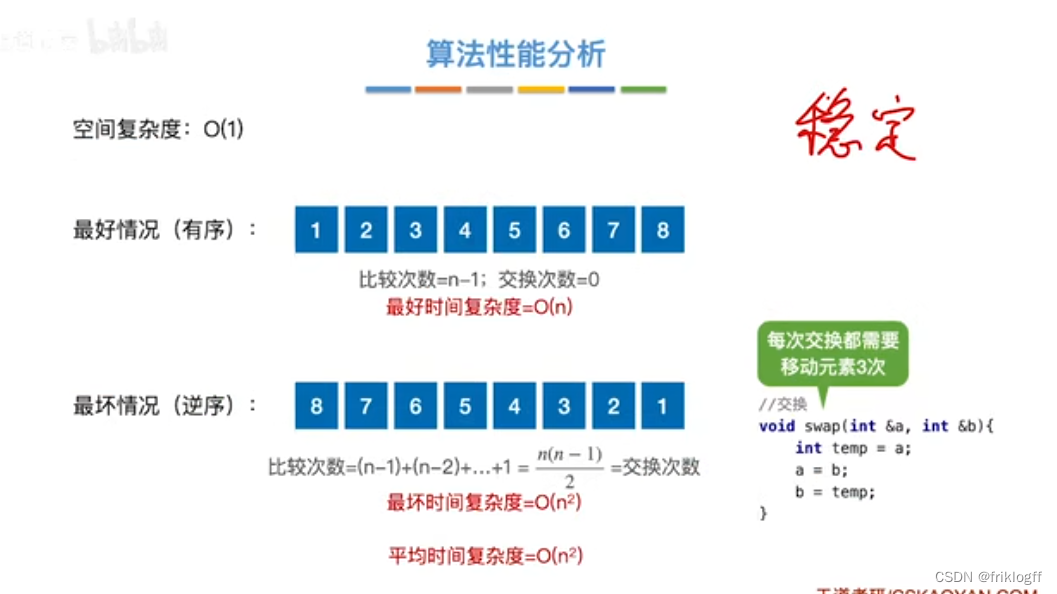
性能分析
-
时间复杂度(平均):O(n^2)
-
最好:O(n)
- 最坏:O(n^2)
-
-
空间复杂度:O(1)
-
-
稳定性
- 稳定
-
补充
- 冒泡排序产生的有序子序列一定全局有序,即每趟会将一个元素放到最终的位置上
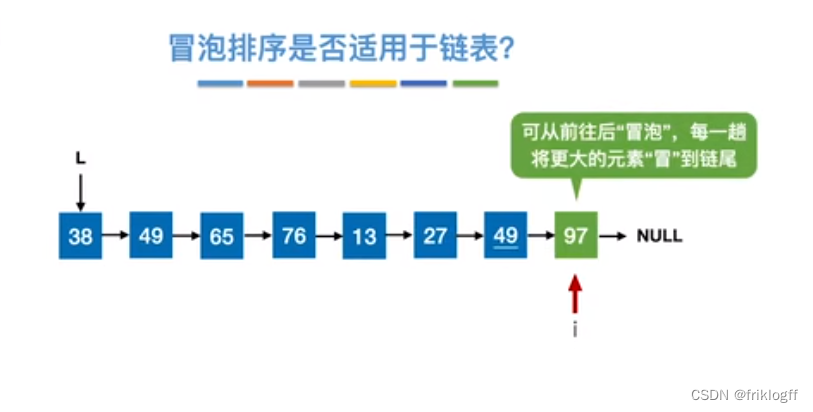
- 冒泡排序产生的有序子序列一定全局有序,即每趟会将一个元素放到最终的位置上
小结
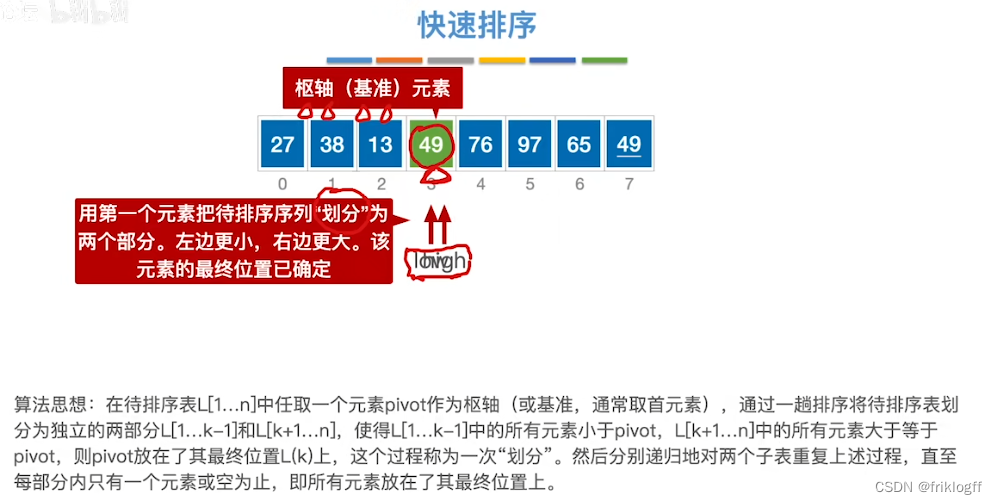
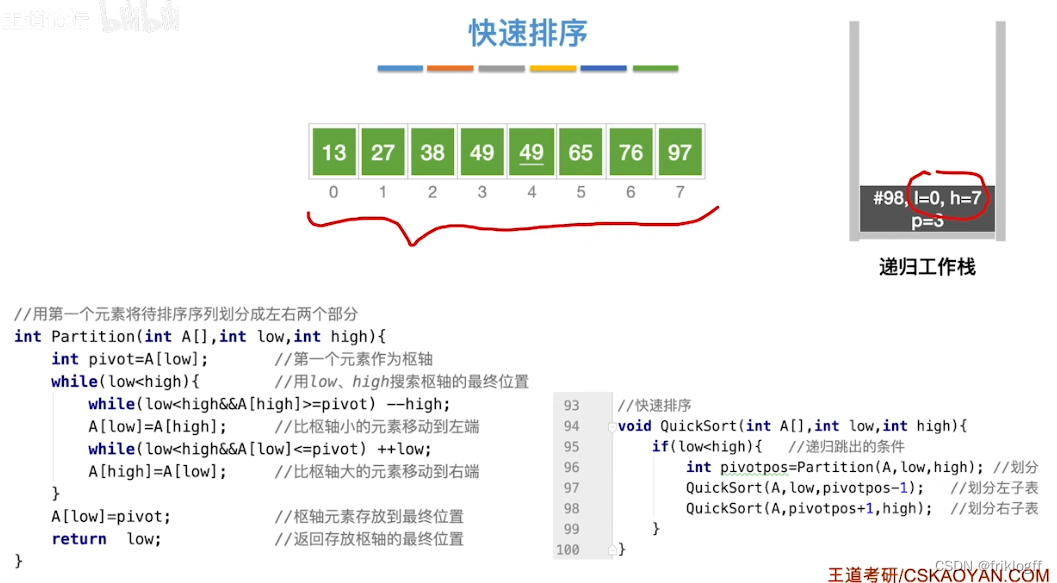
快速排序
-
实现过程
-
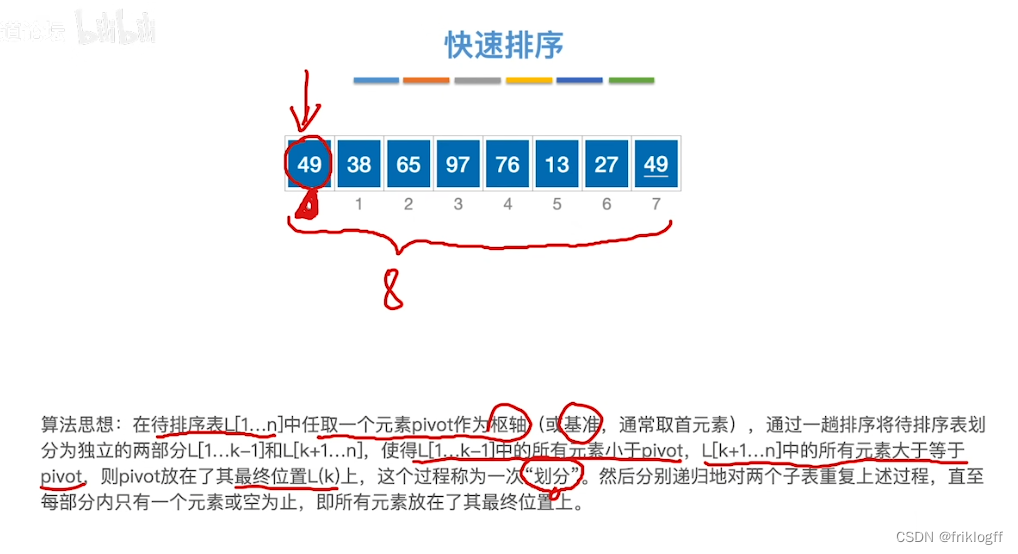
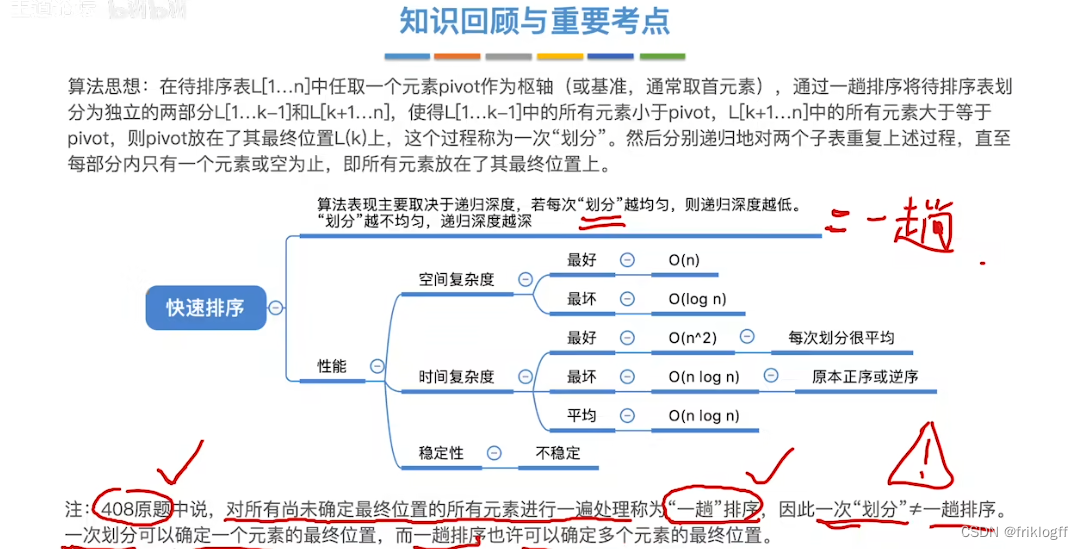
首先选取一个元素作为枢轴,以枢轴为界将排序表分为两个部分,左边小于枢轴,右边大于枢轴
-
然后对着两部分分别递归重复上述步骤,直到每个部分内只有一个元素或空为止
-
-
性能分析
-
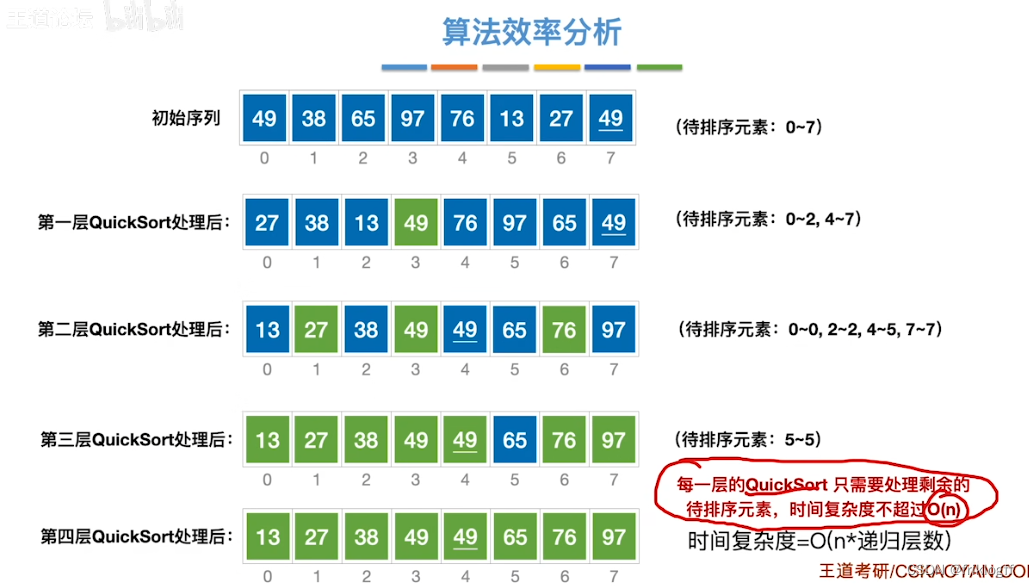
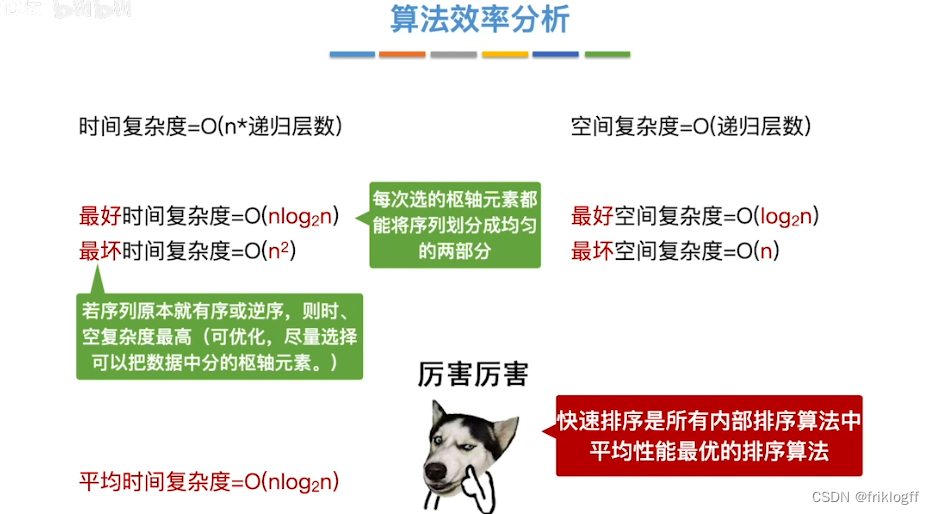
时间复杂度
-
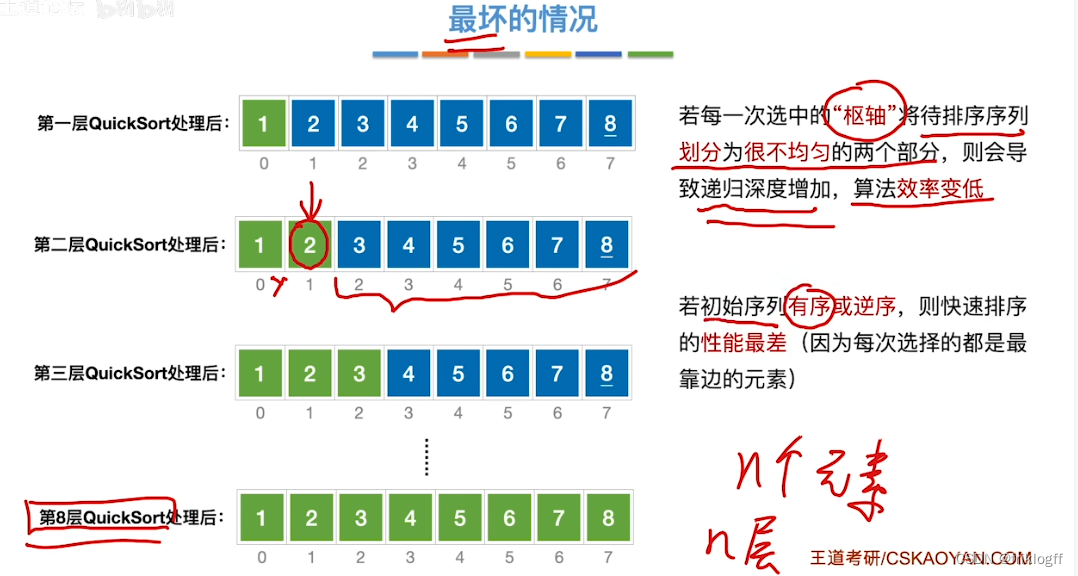
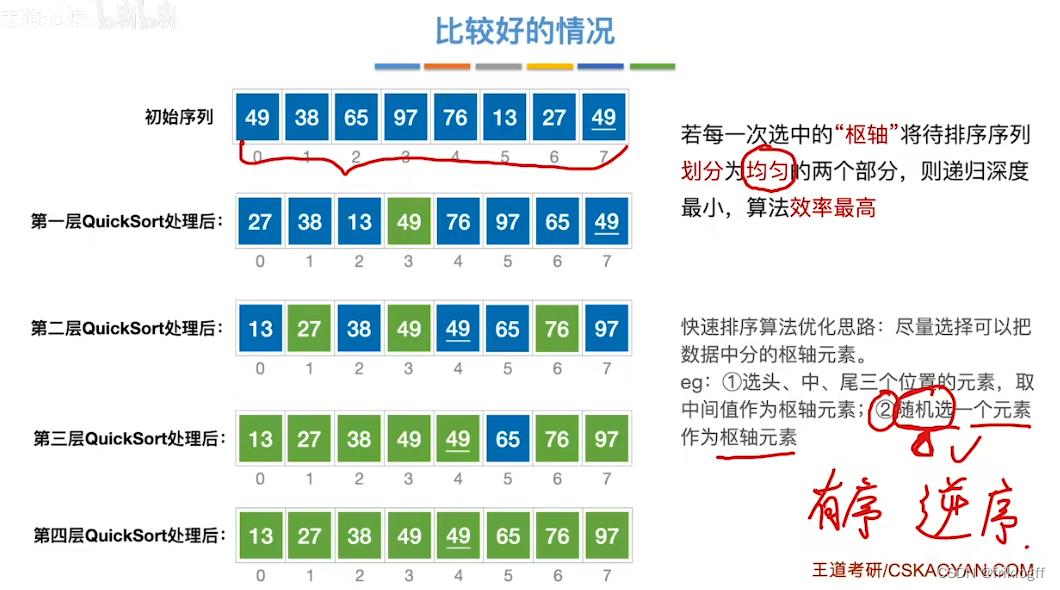
快速排序的运行时间与划分是否对称有关,应尽量选取可以将数据中分的枢轴元素(想象一颗二叉树)
-
最好情况:待排序列越无序,算法效率越高:O(nlog2n)
-
最坏情况:待排序列越有序,算法效率越高:O(n^2)
-
平均情况:快速排序平均情况下与最优情况下运行时间很接近,是所有内部排序算法中平均时间最优的排序算法
-
-
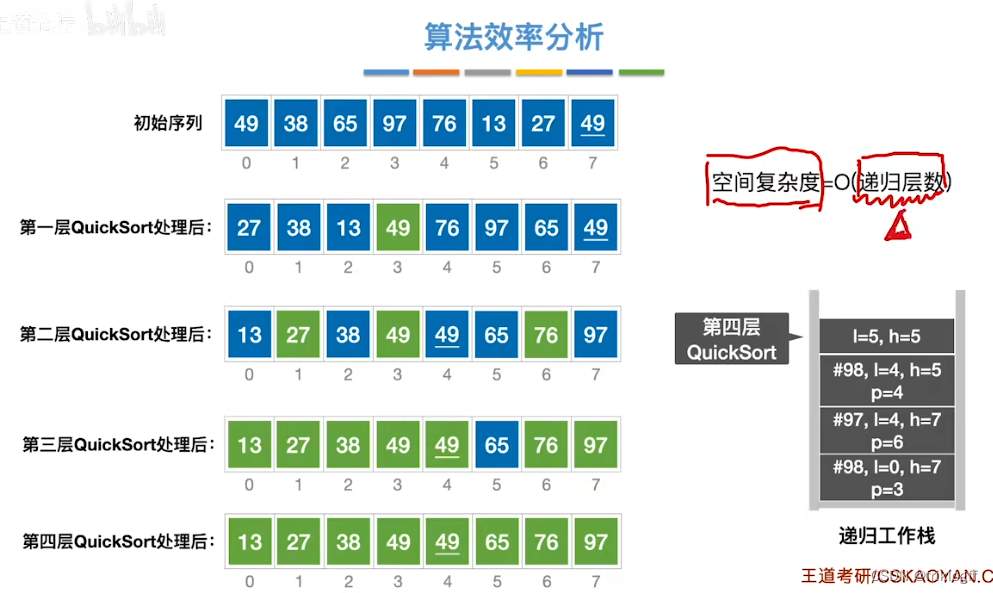
空间复杂度(平均):O(log2n)

-
最好:O(log2n)
- 最坏:O(n)
-
-
-
稳定性
- 不稳定
-
优化:划分均匀
-
选头中尾三个位置的元素,取中间值为枢轴元素
-
随机选一个元素作为枢轴元素
-


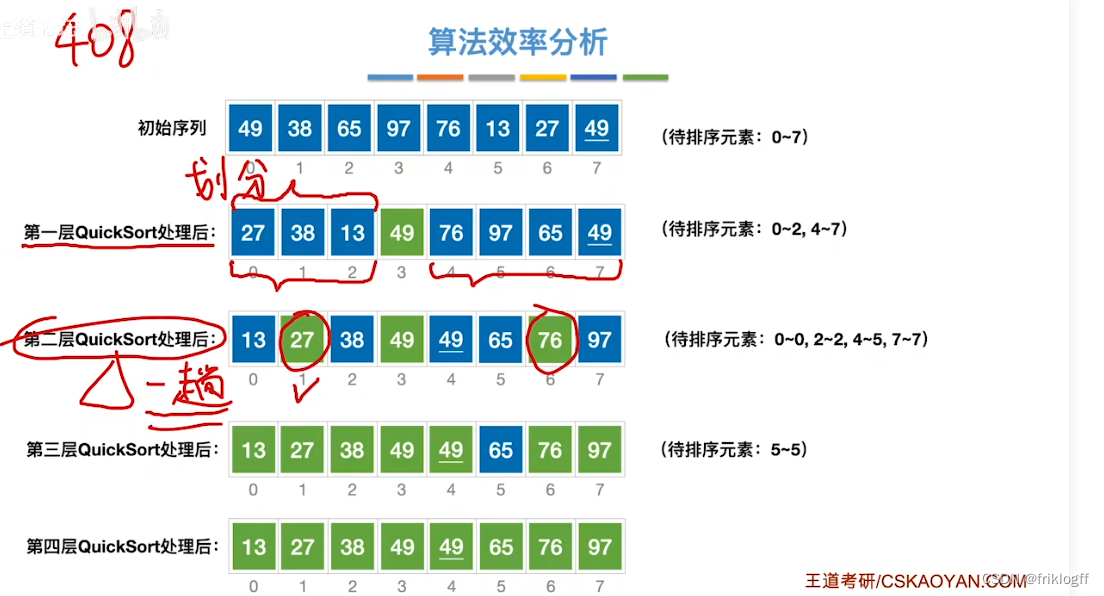
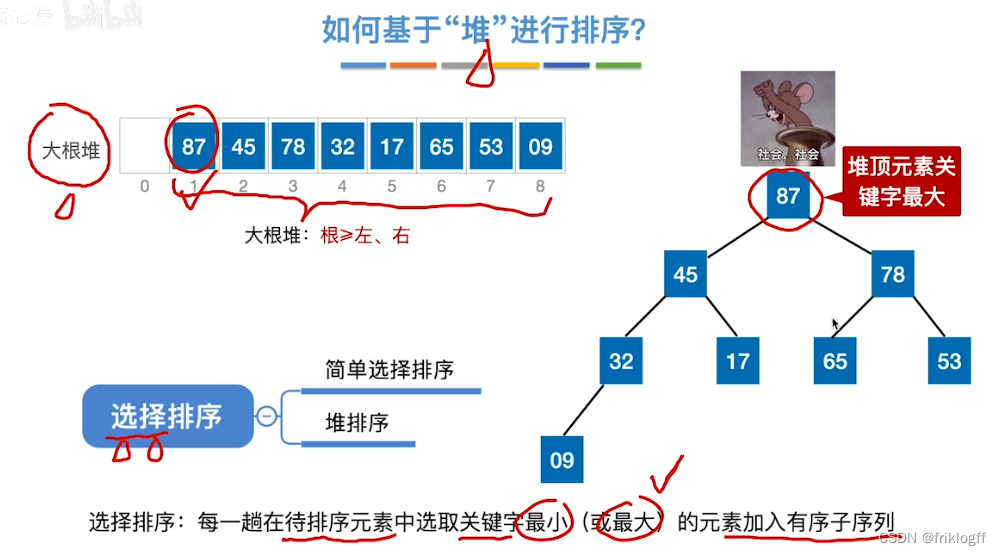
选择排序
概述
-
每一趟(如第i躺)在后面n-i+1(i=1,2,…,n-1)个待排序元素中选取关键字最小的元素,作为有序子序列的第i个元素,直到第n-1趟完成
-
选择排序的时间性能不随记录序列中关键字的分布而改变
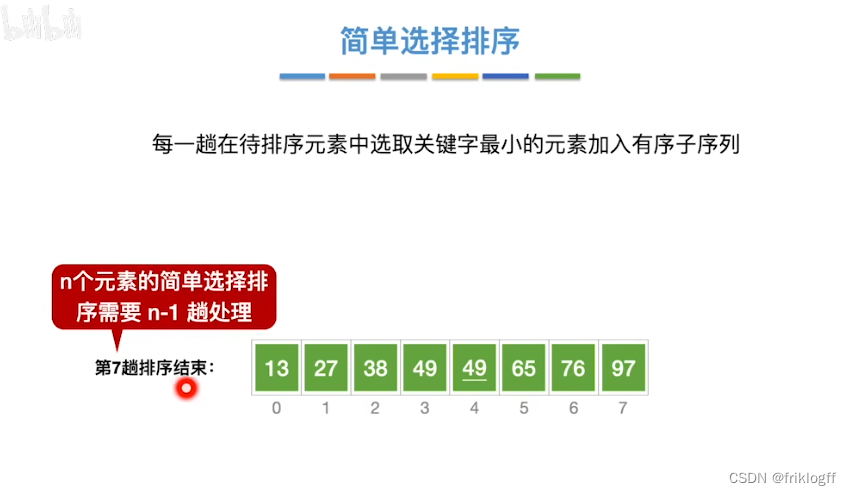
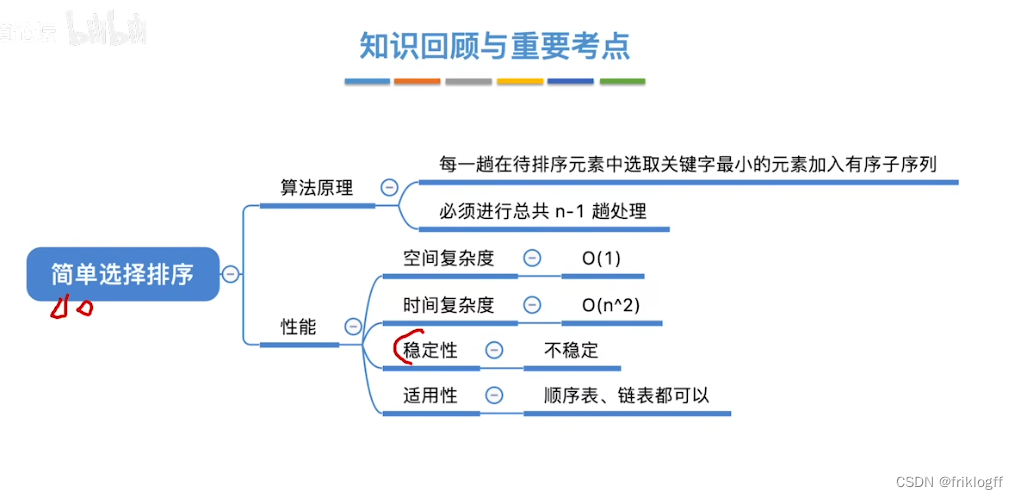
简单选择排序
-
实现过程
-
假设排序表为L[1…n],第i躺排序,即从L[1…n]中选择关键字最小的元素与L(i)交换
-
i每次增加,每趟排序可以确定一个元素的最终位置
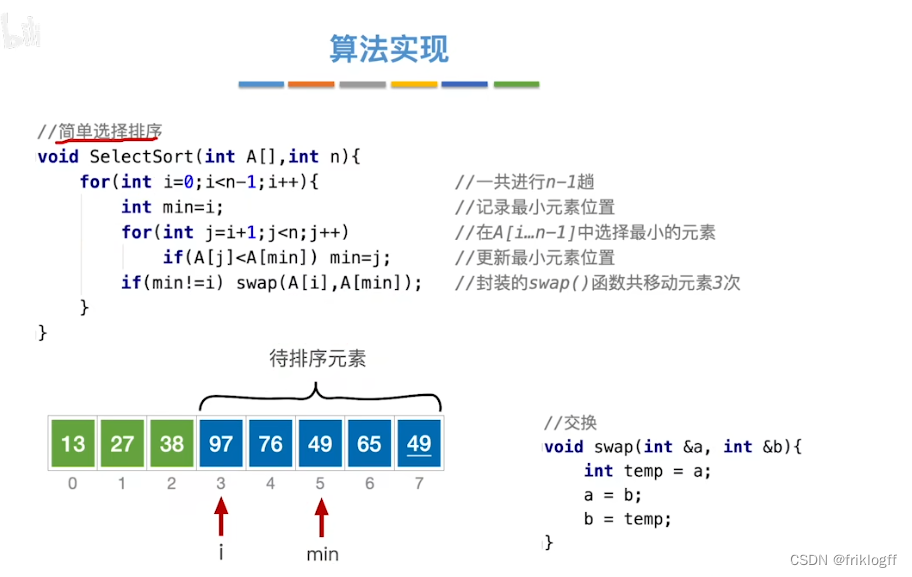
-
-
性能分析
-
时间复杂度:O(n^2)
-
空间复杂度:O(1)
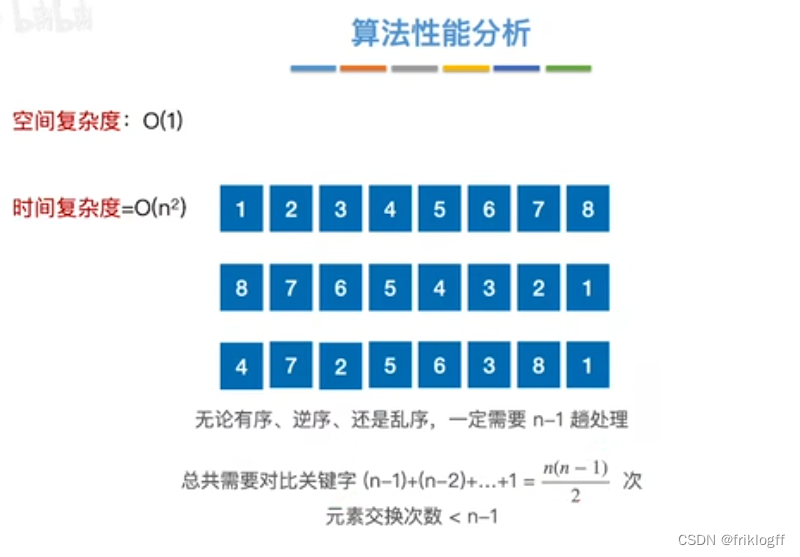
-
-
稳定性
- 不稳定
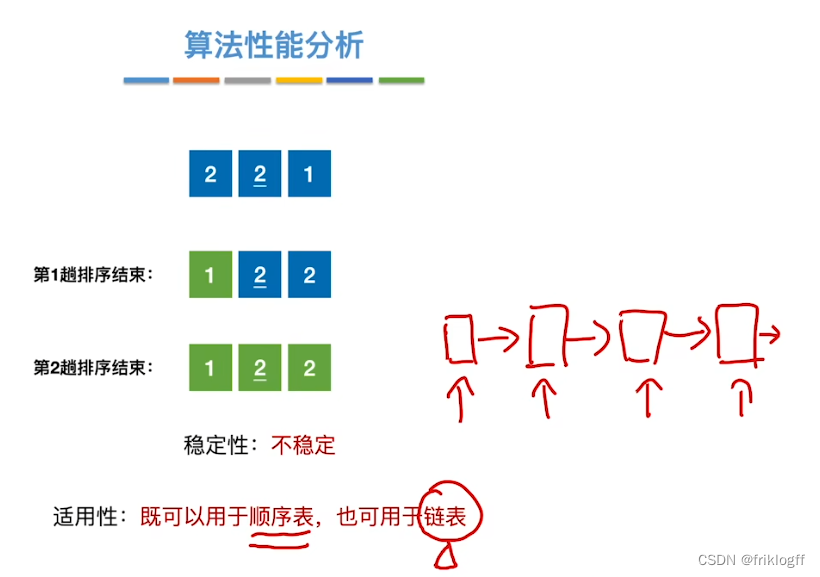
- 不稳定
小结
堆排序
-
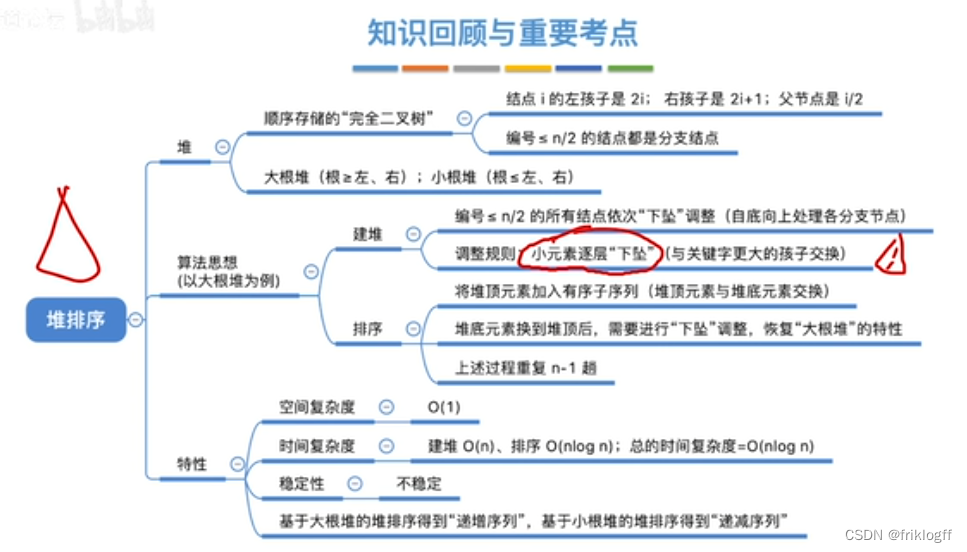
基本概念
-
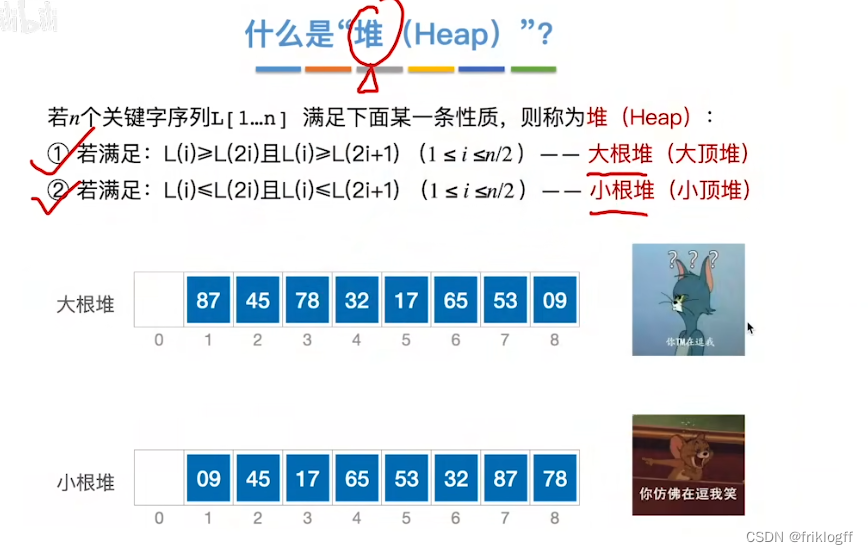
堆
- 堆是一棵完全二叉树,而且满足任何一个非叶结点的值都不大于(或不小于)其左右孩子结点的值
-
大根堆
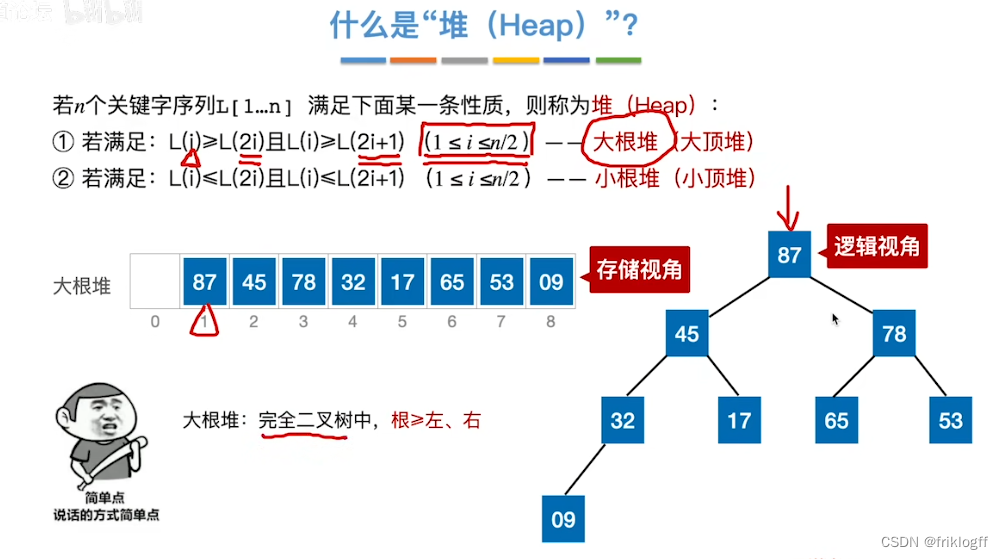
- 每个结点的值都不小于它的左右孩子结点的值
-
小根堆
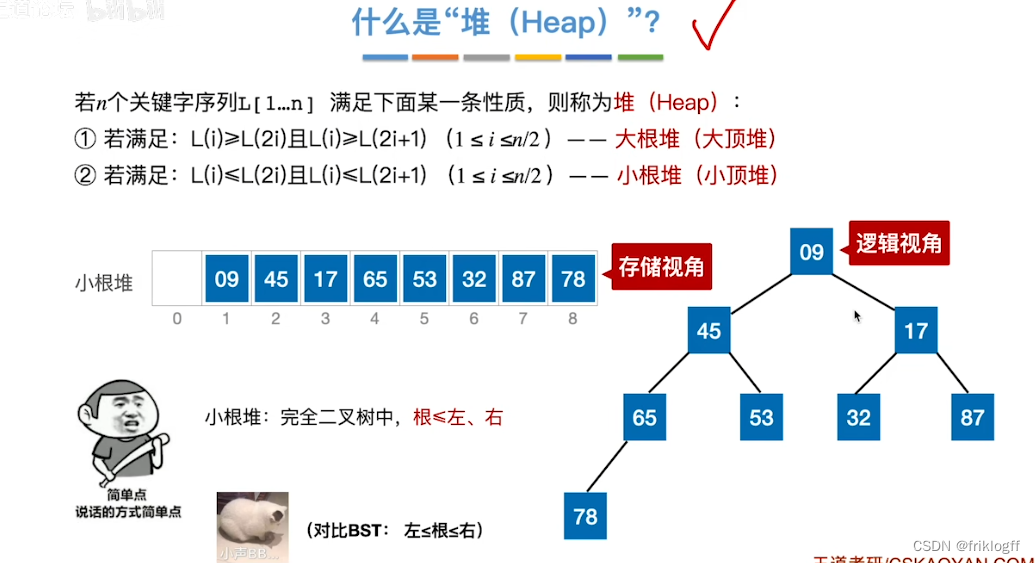
- 每个结点的值都不大于它的左右孩子结点的值
- 每个结点的值都不大于它的左右孩子结点的值
-
-
实现过程
-
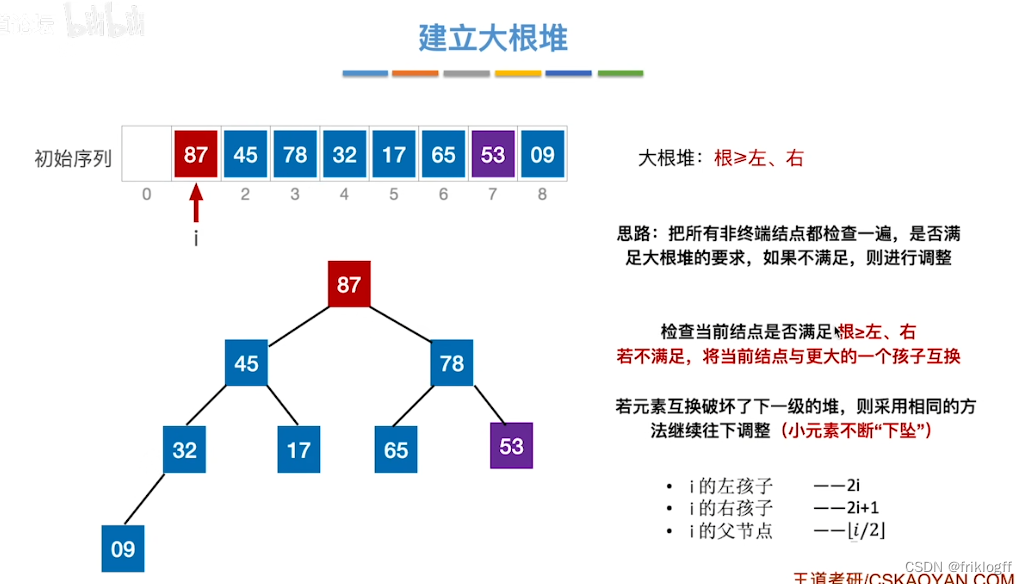
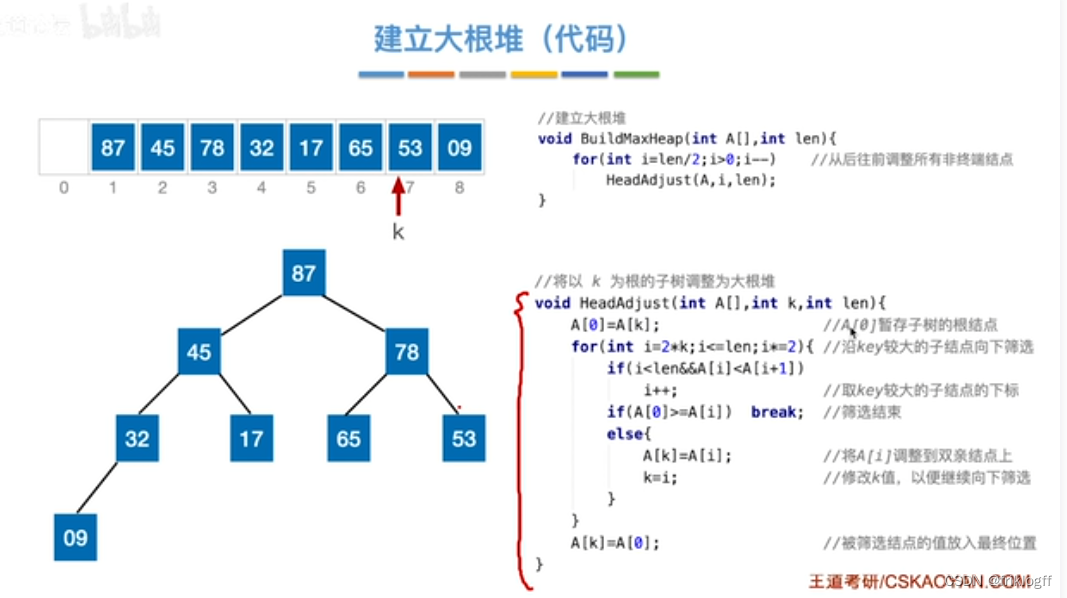
建大(小)根堆:O(n)
-
从后向前调整所有非终端结点,使其满足堆的性质[0, ⌊n/2⌋]
-
检查是否根大于(小于)等于左右孩子,小(大)元素不断下坠(下坠过程需不断检查与左右孩子的大小)
-
-
调整大(小)根堆:O(nlog2n)
-
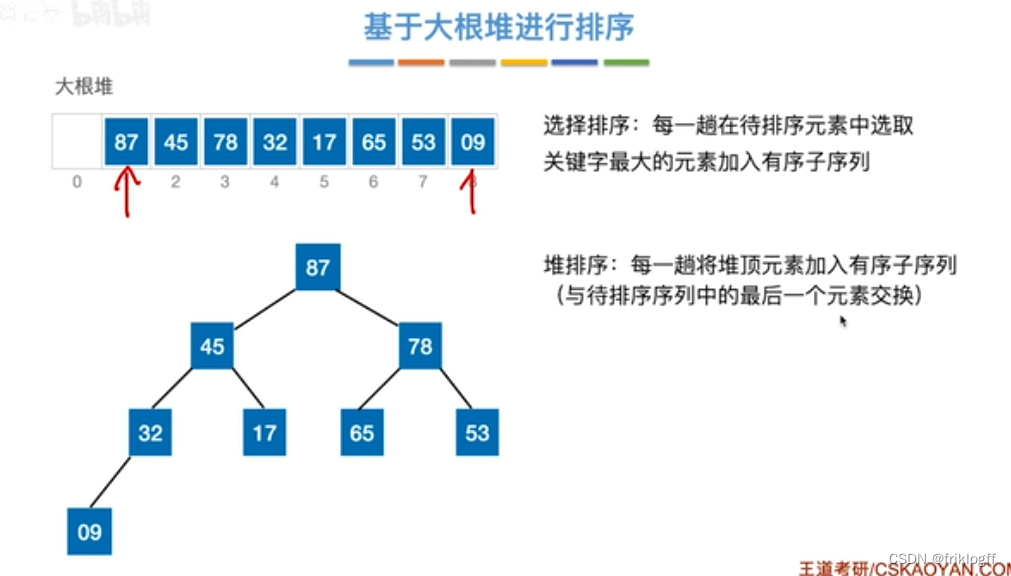
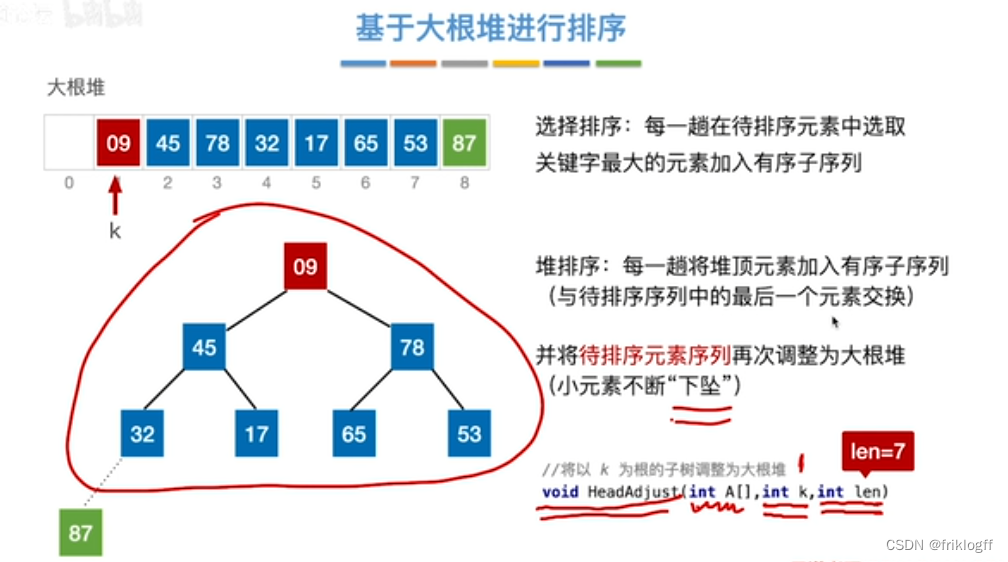
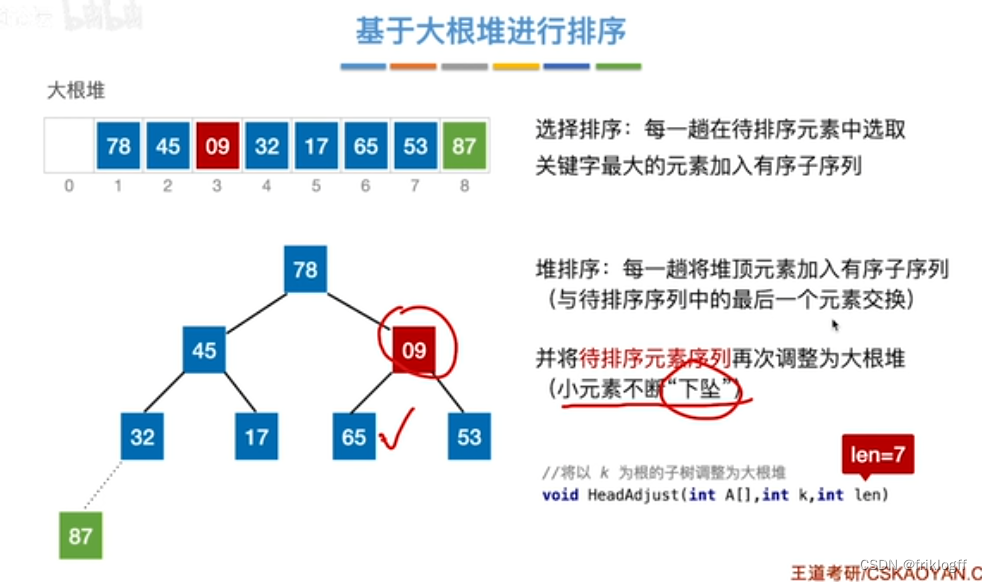
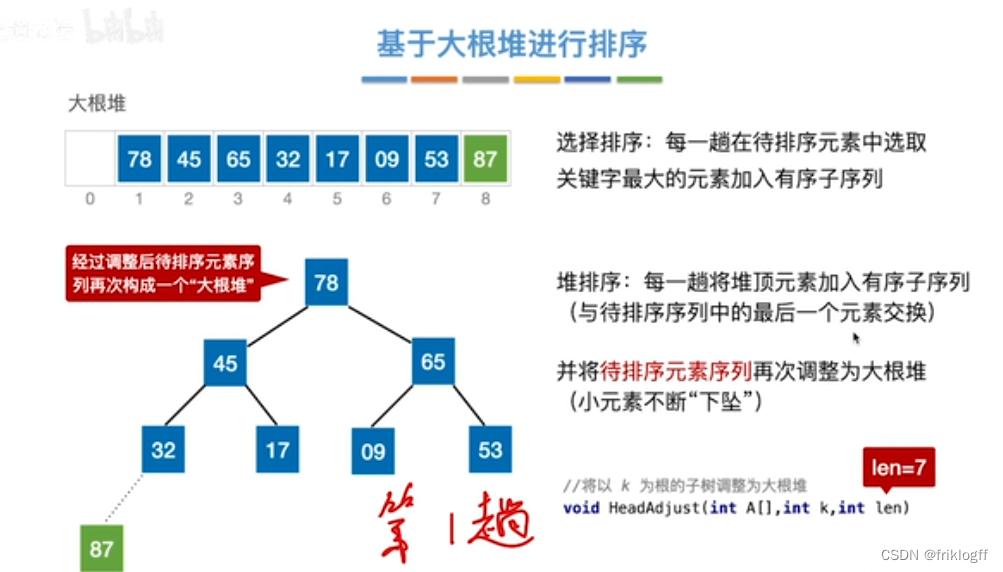
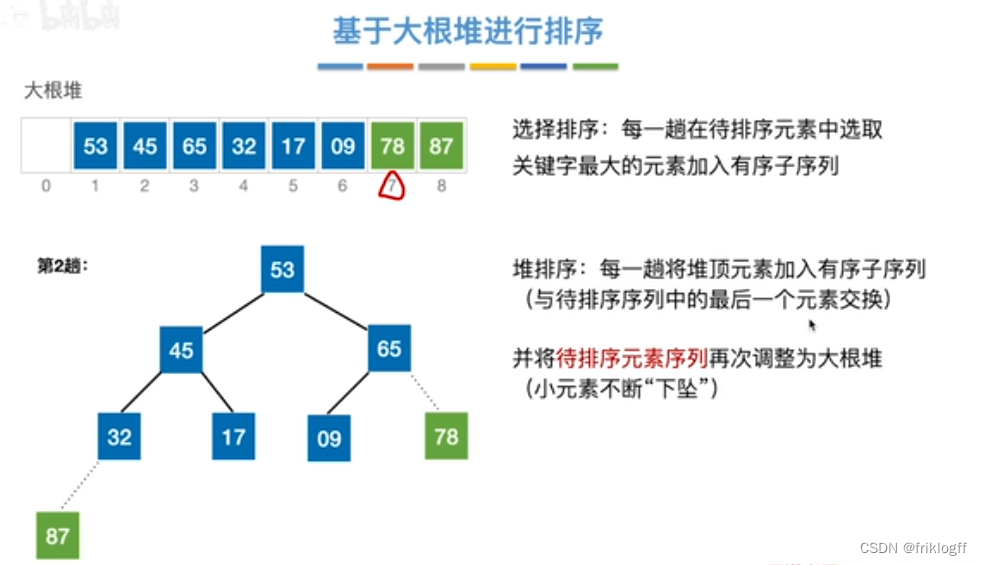
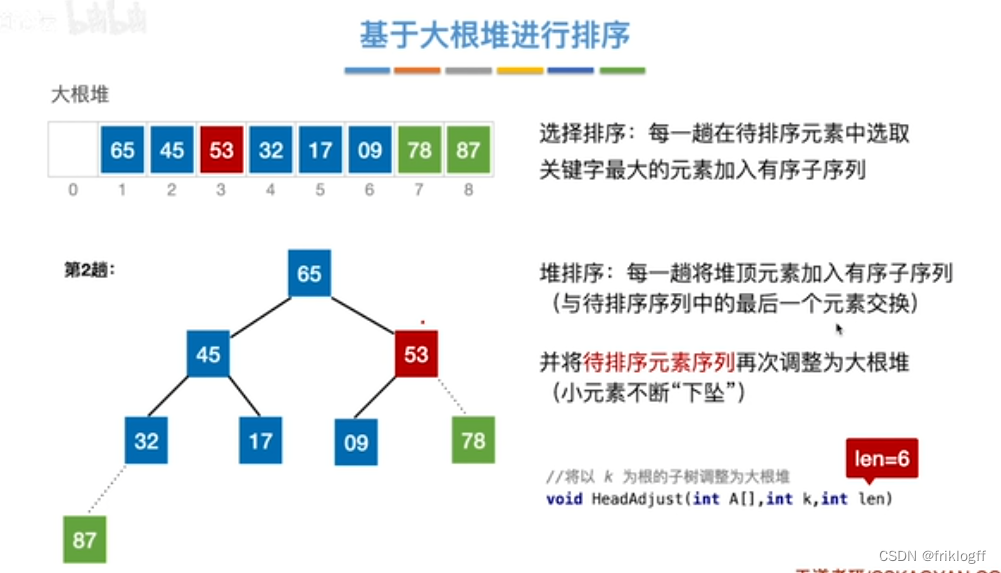
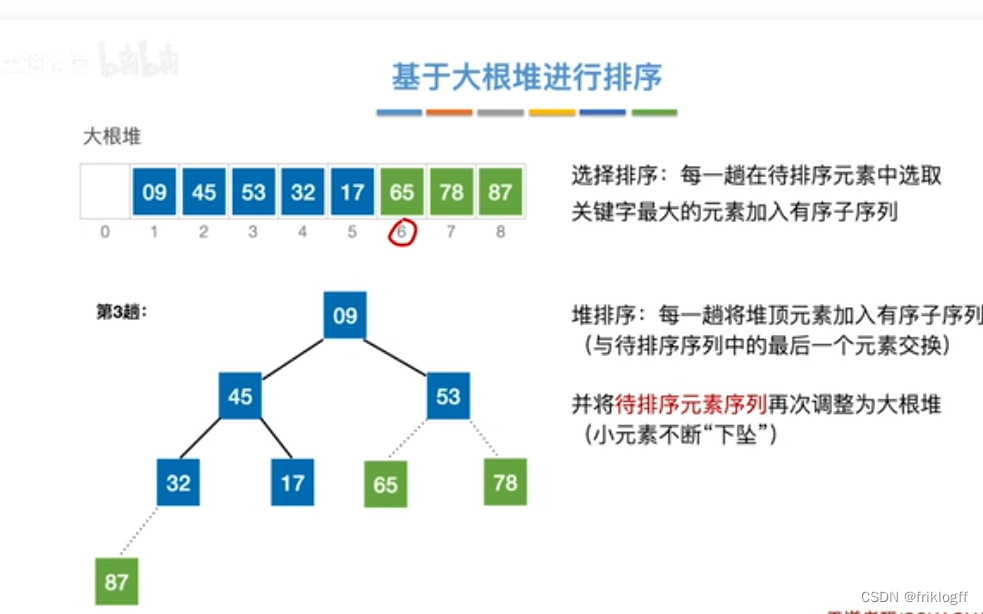
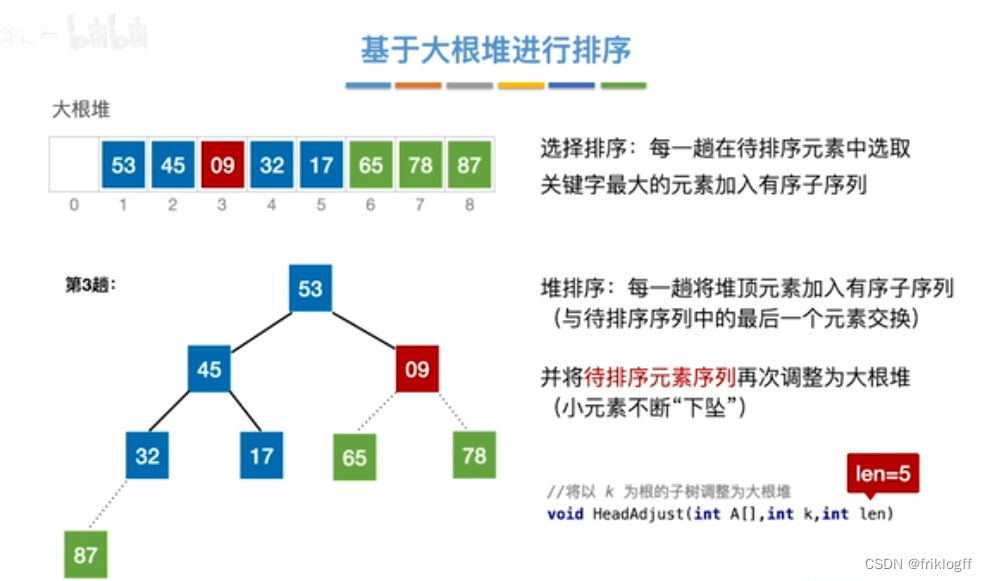
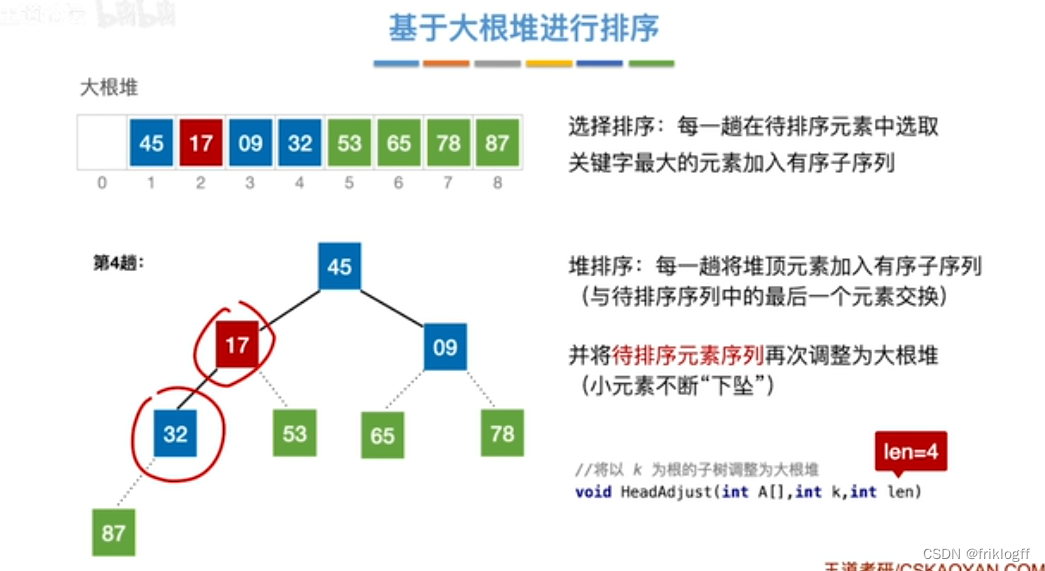
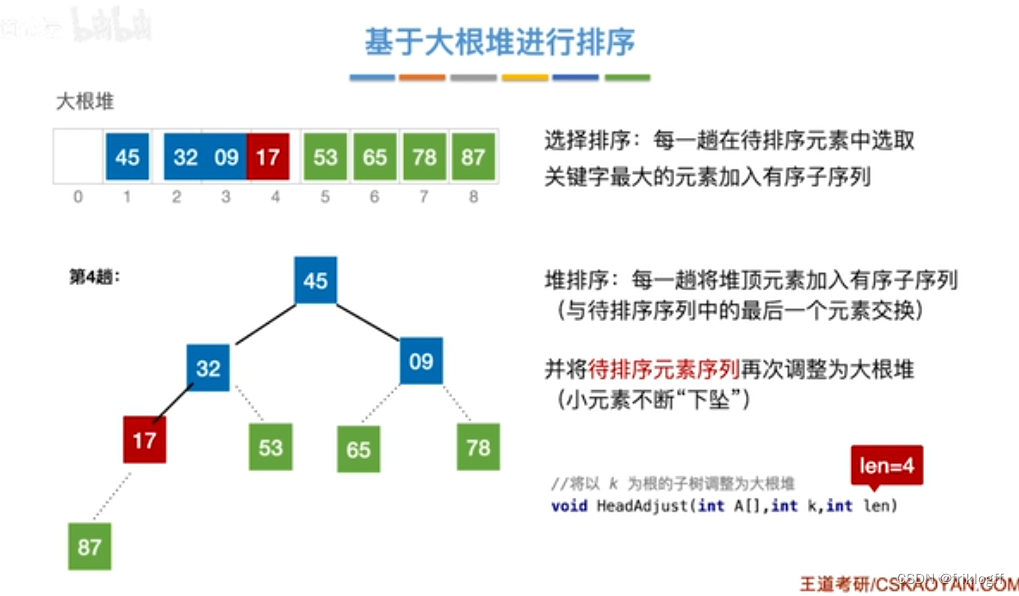
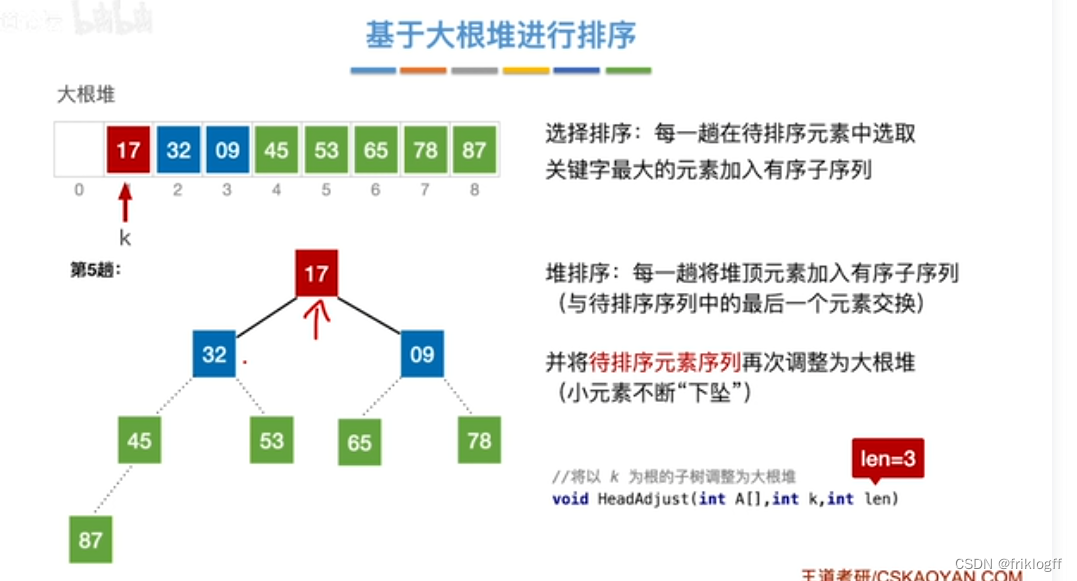
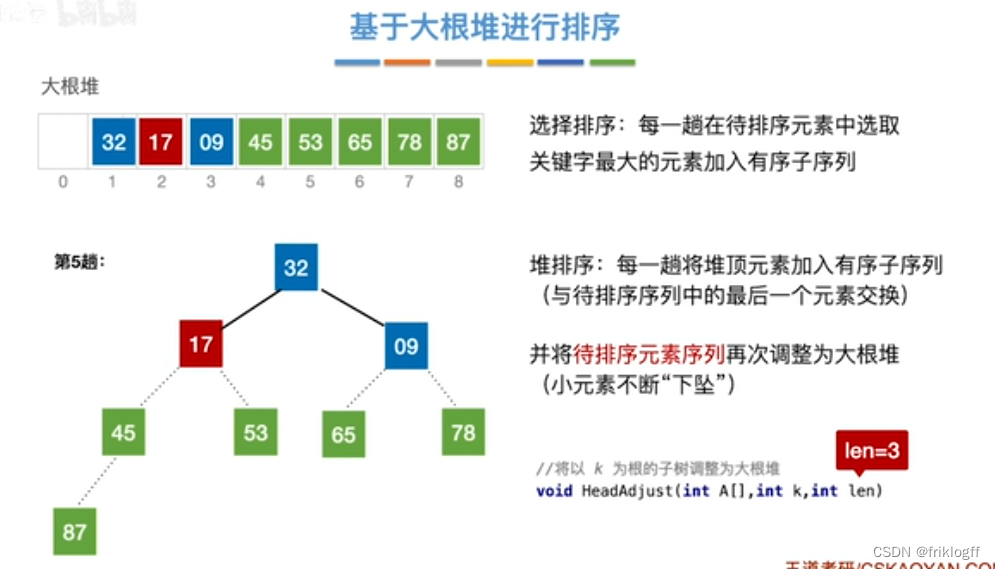
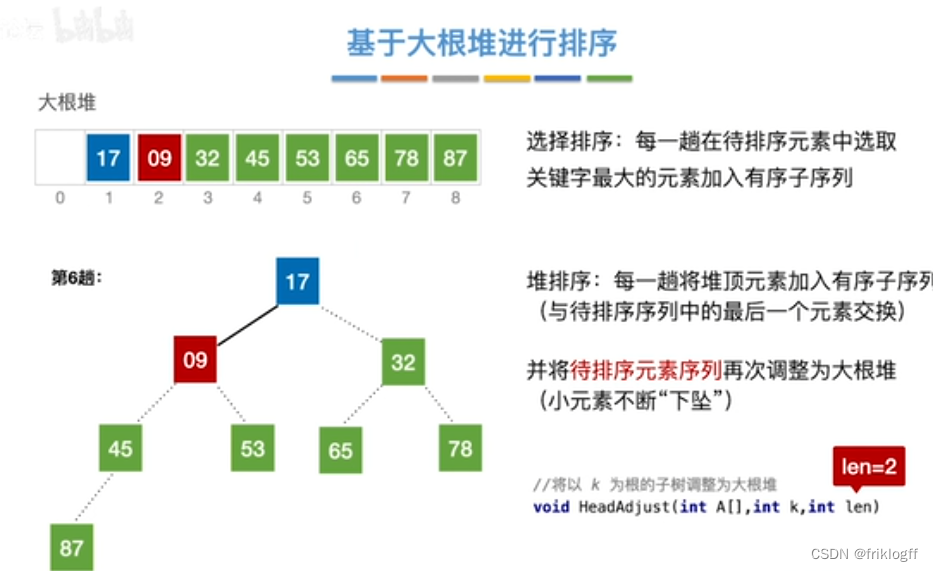
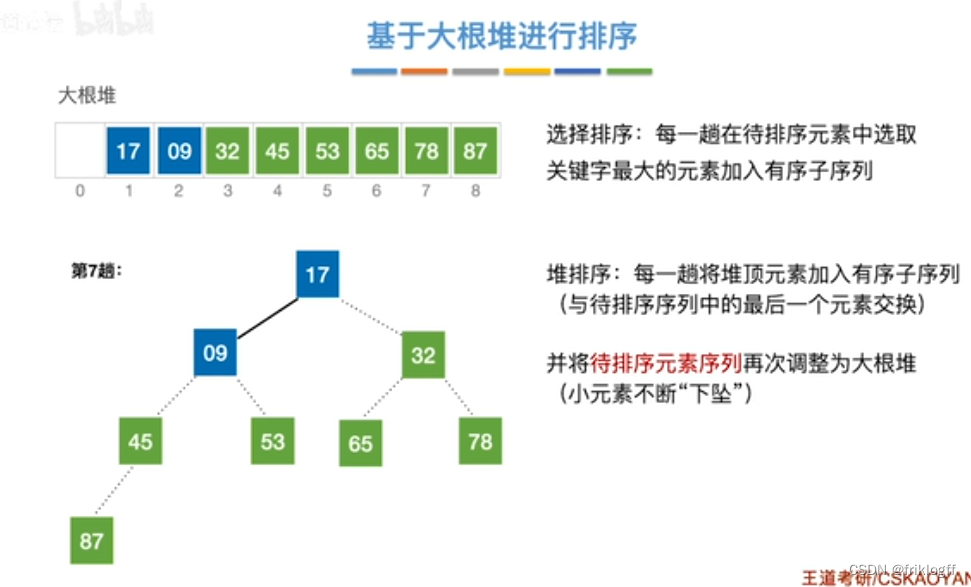
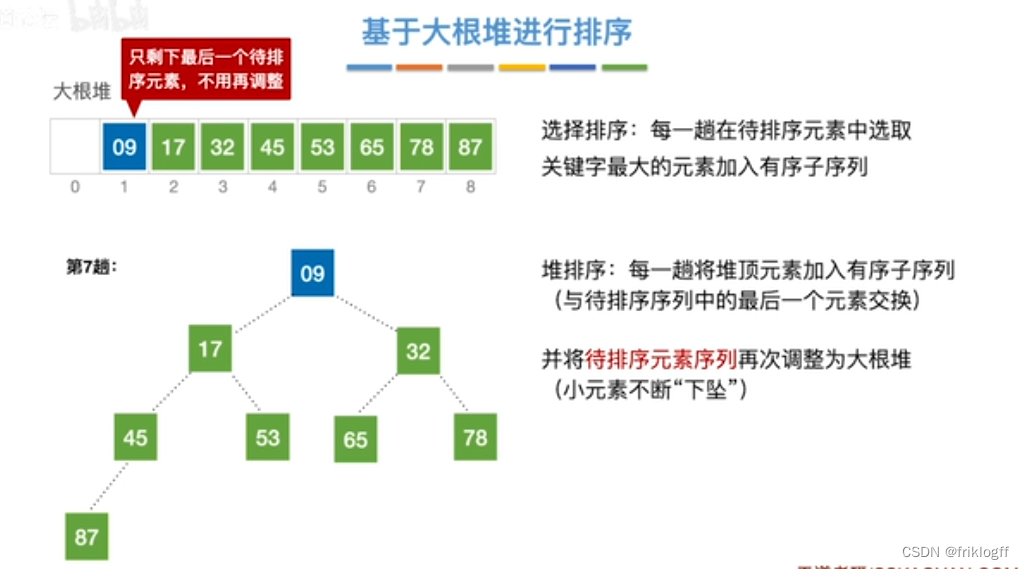
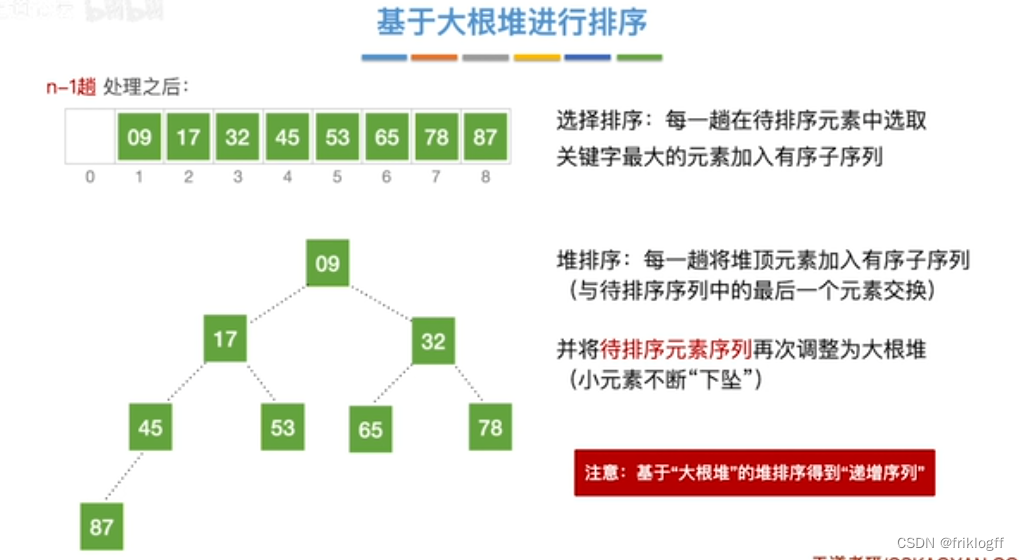
将最大(小)根结点与最后一个结点互换
-
按建堆过程调整结点

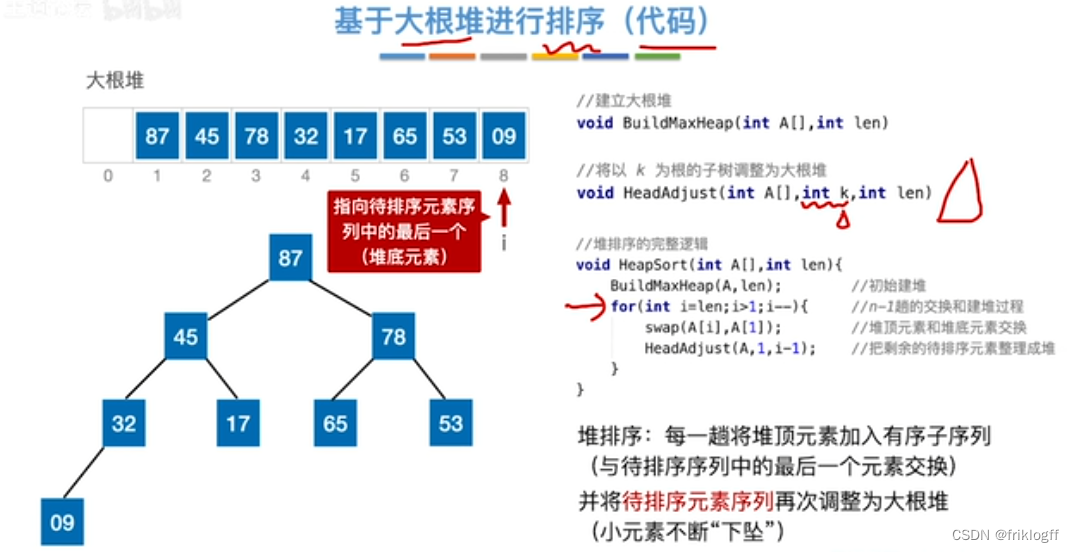

-
-
-
性能分析
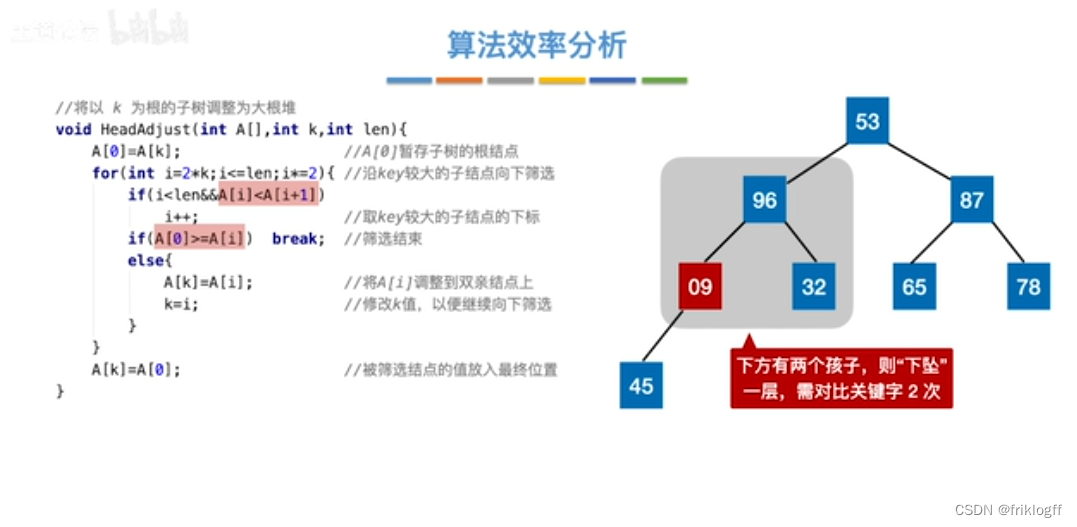
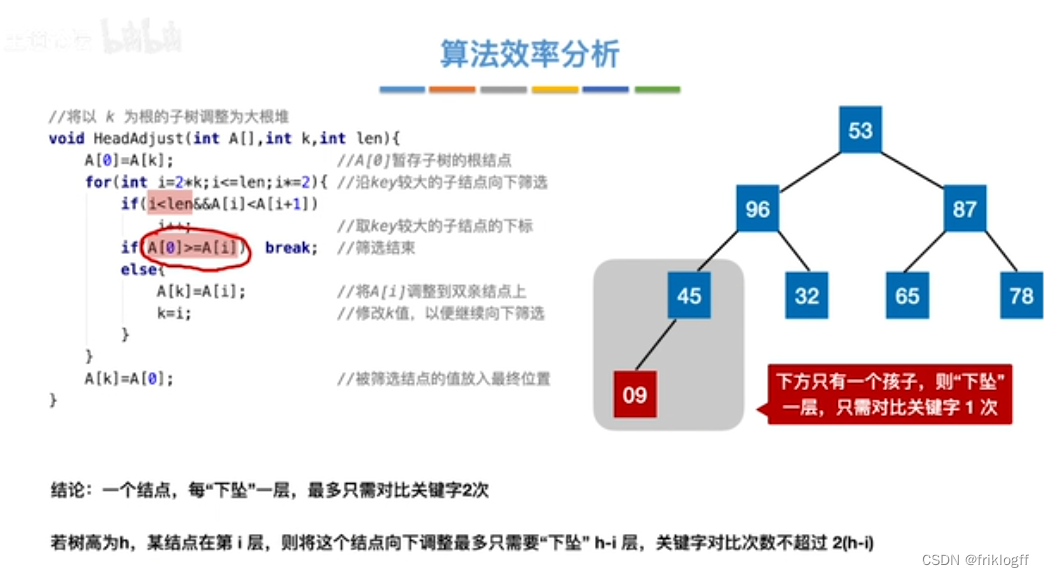
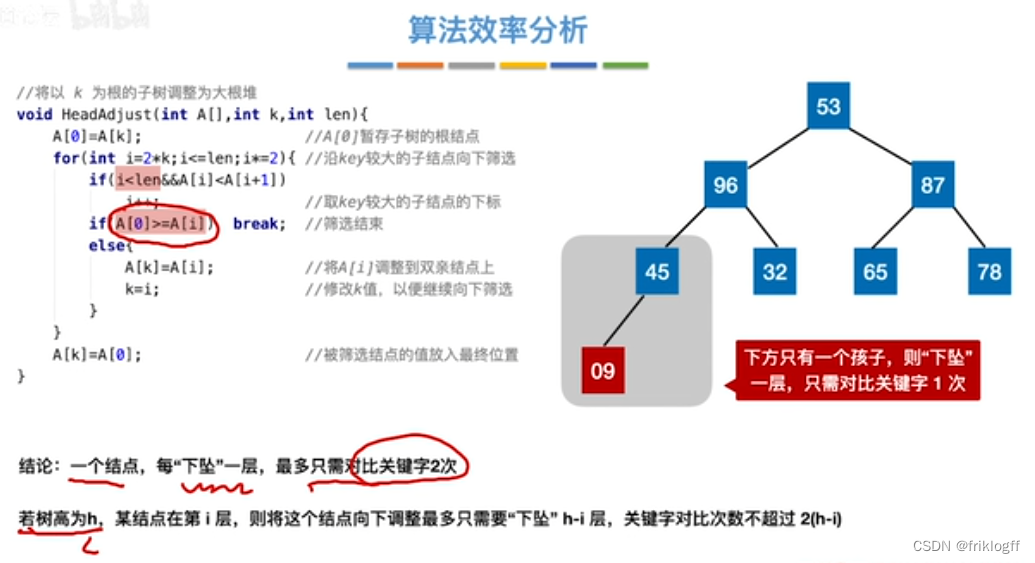

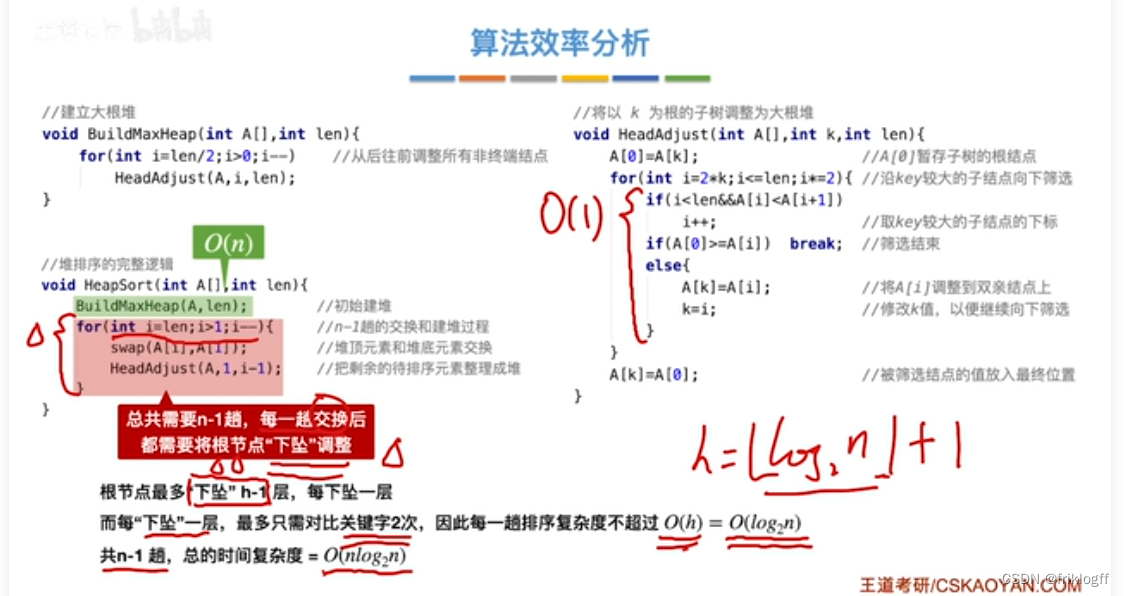

-
时间复杂度:O(nlog2n)
-
空间复杂度:O(1)
-
-
稳定性
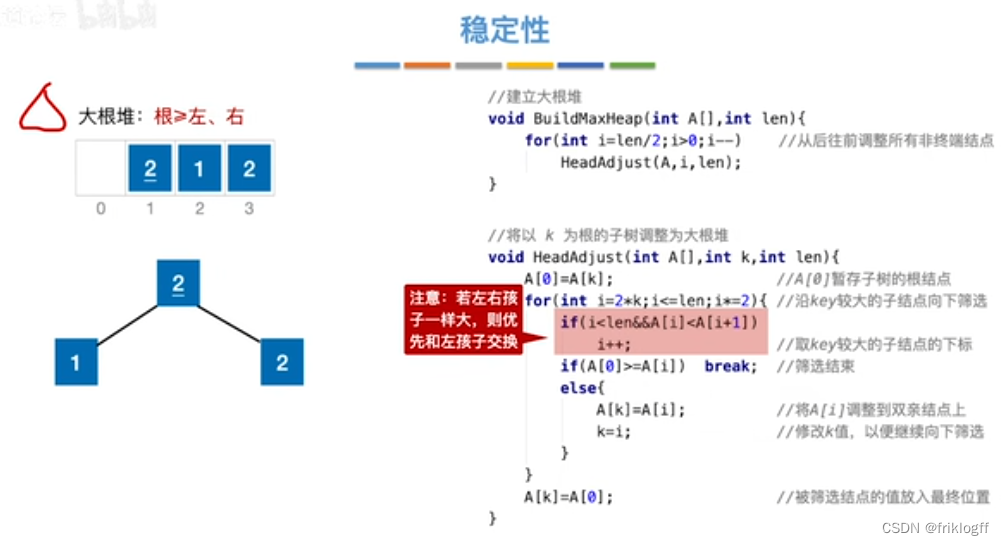
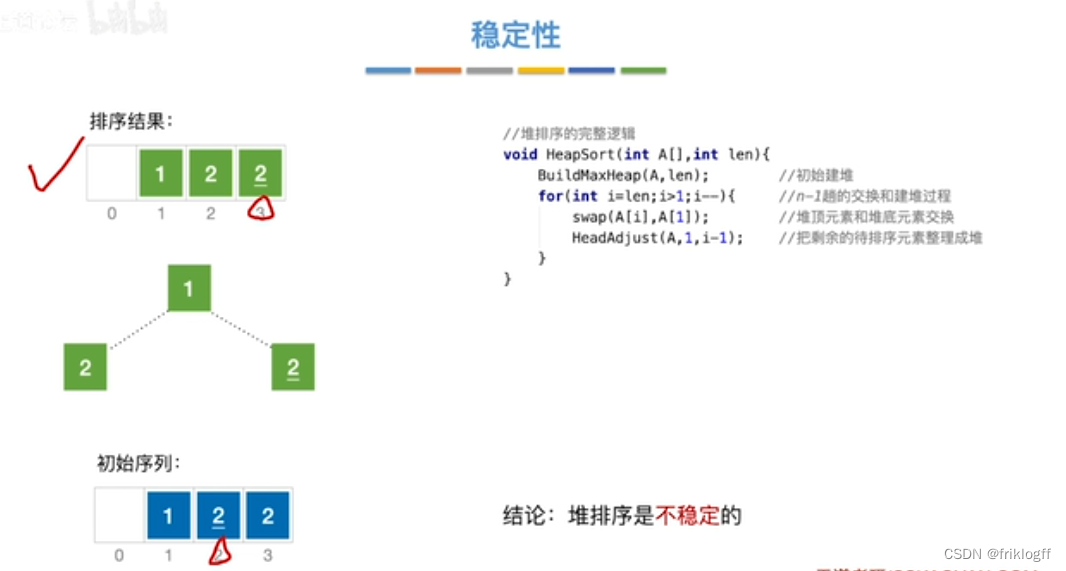
- 不稳定
小结
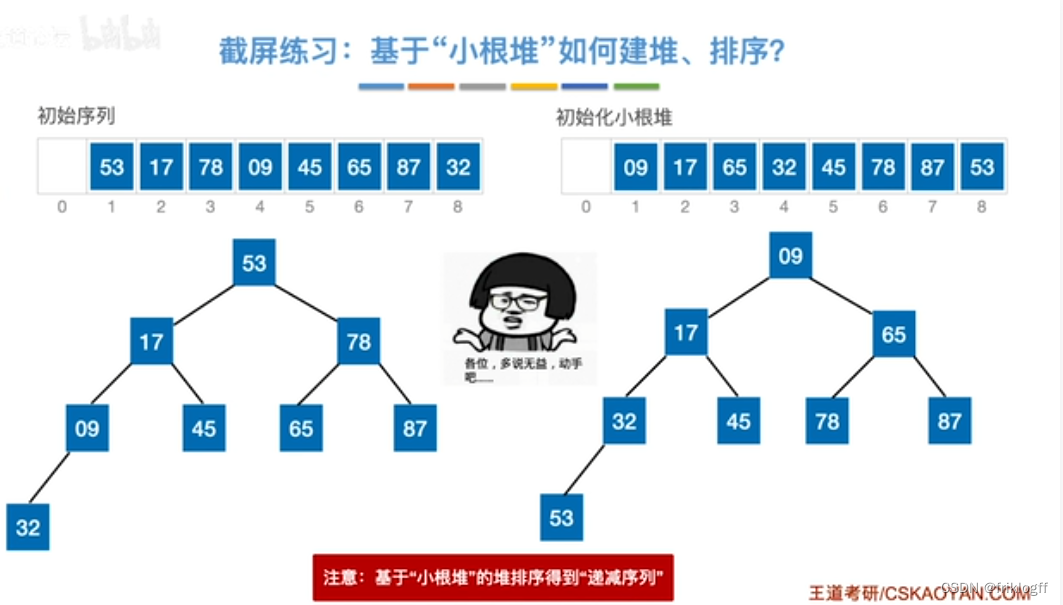
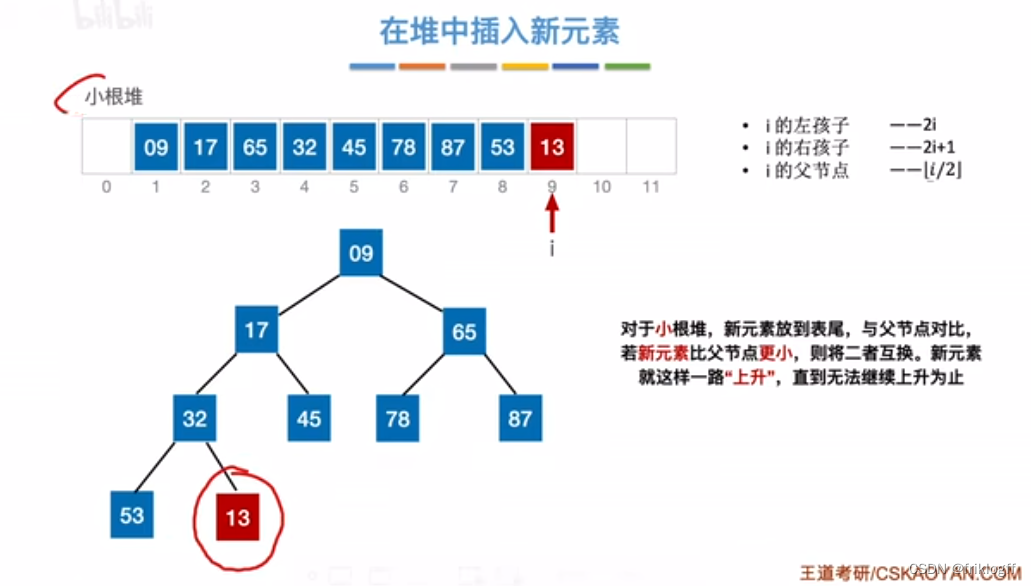
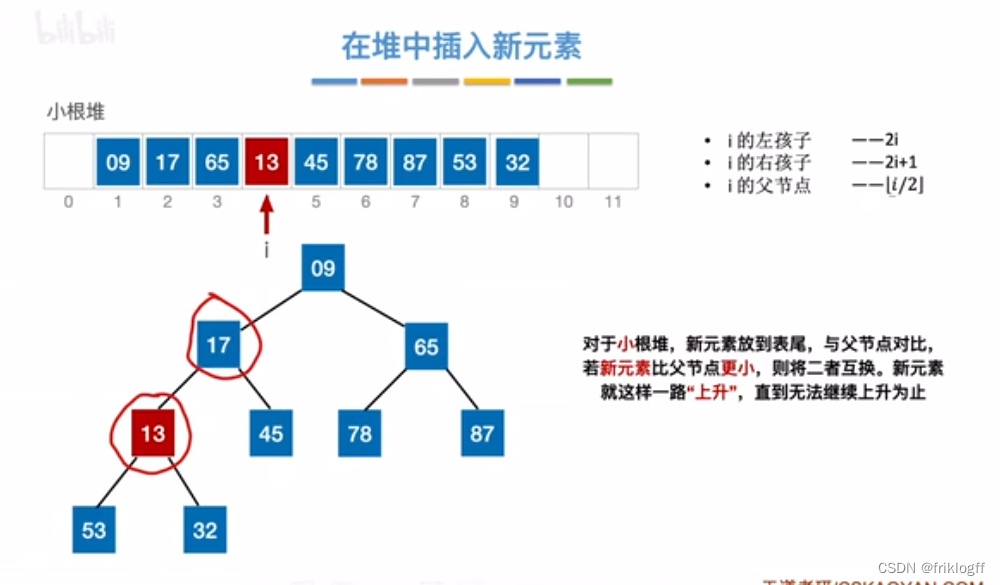
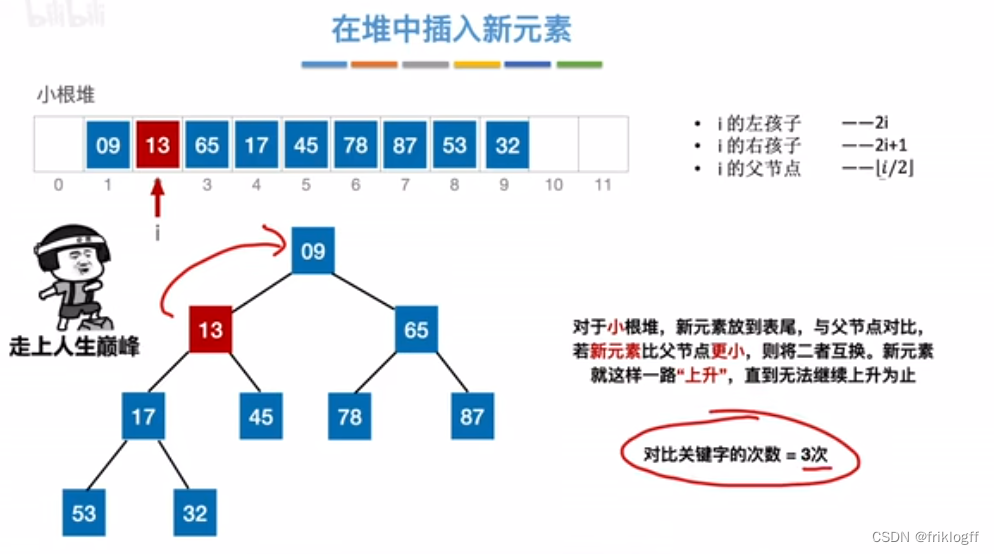
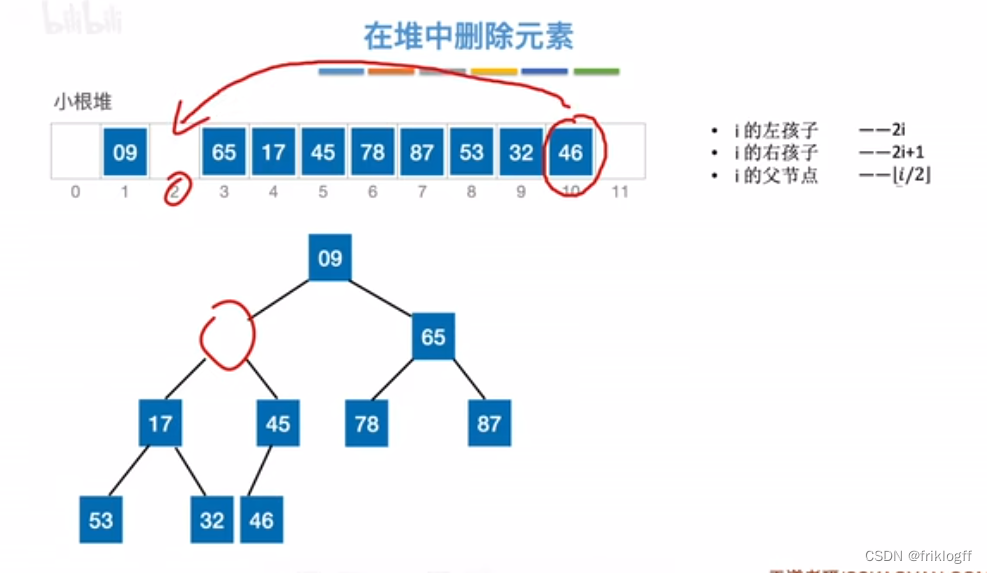
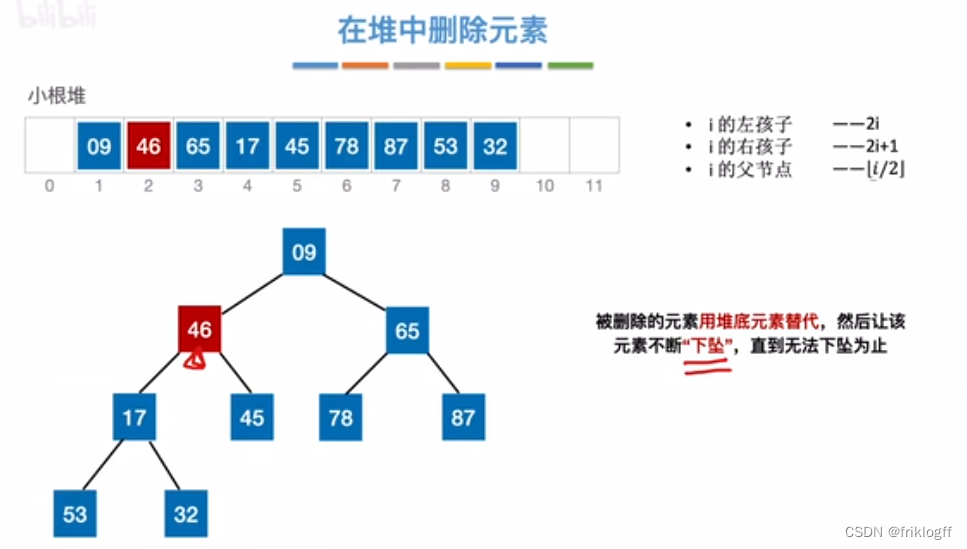
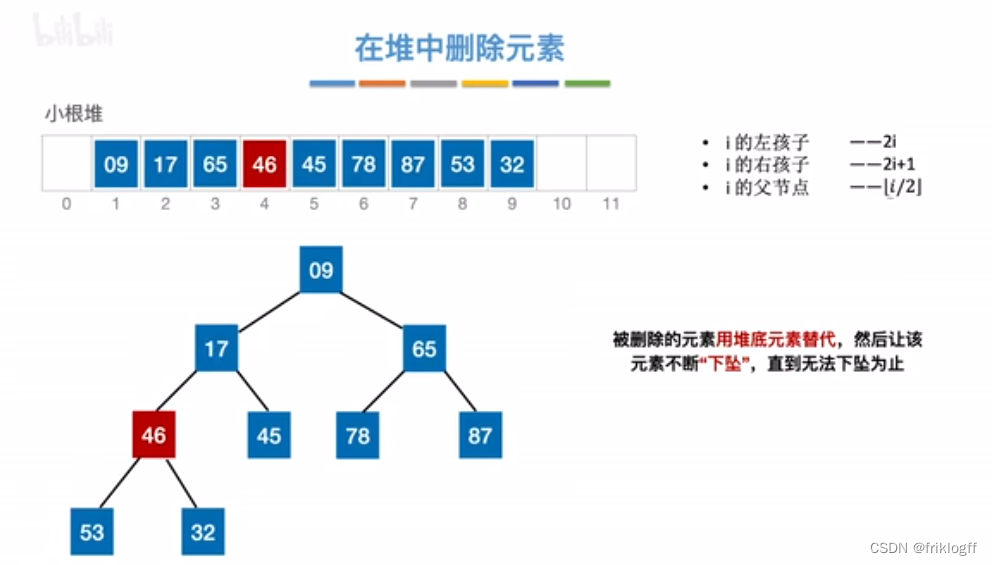
堆的插入删除
插入
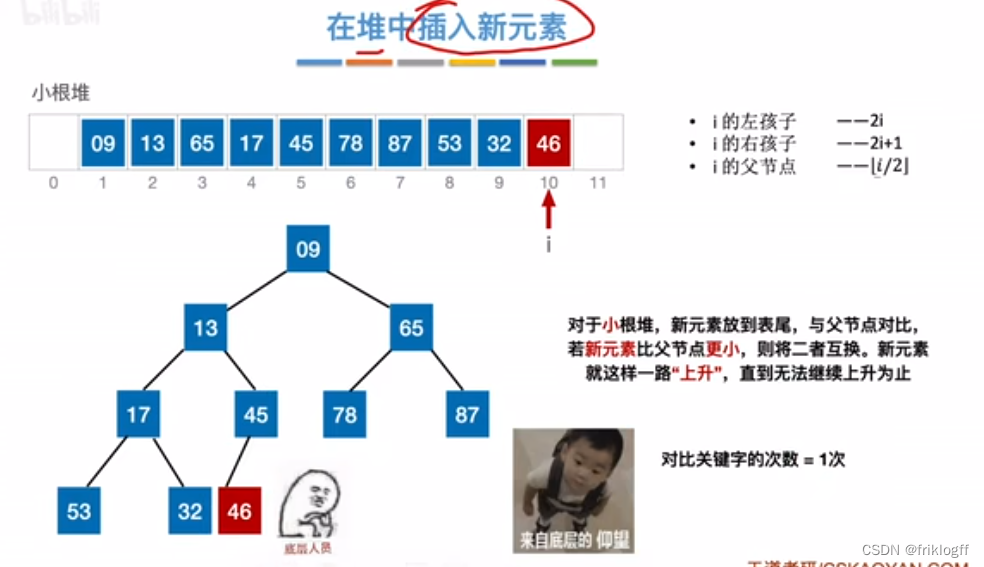
删除
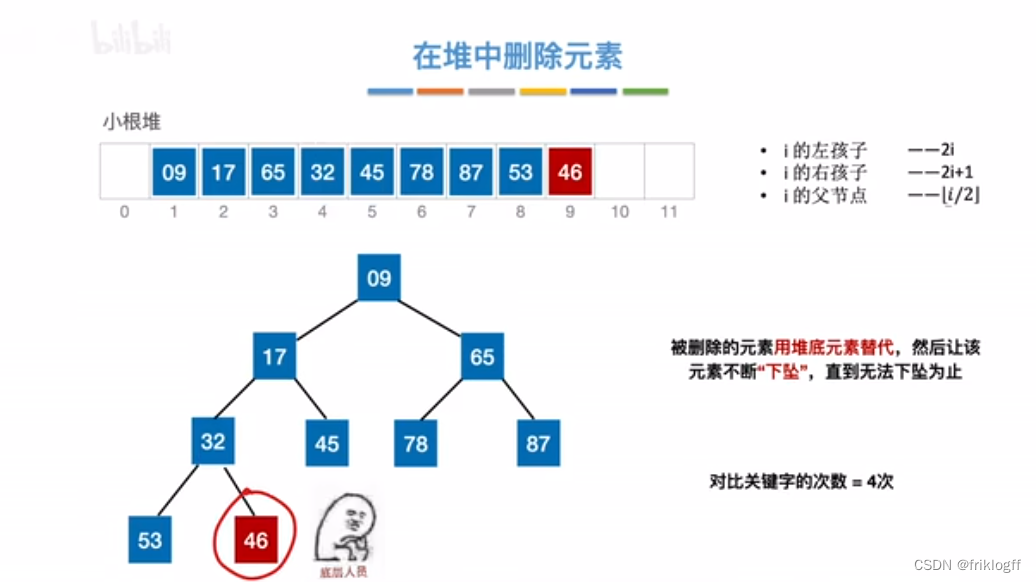
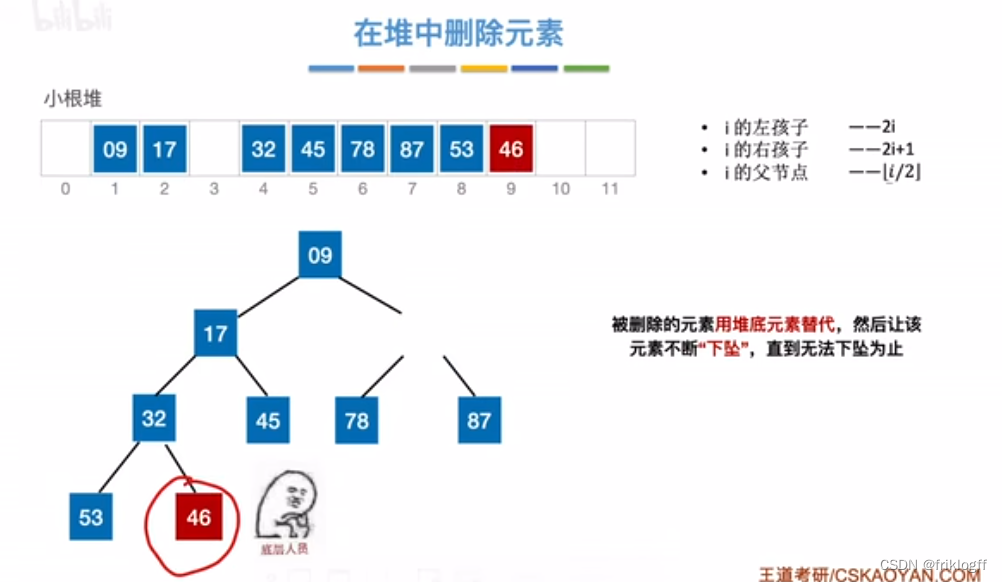
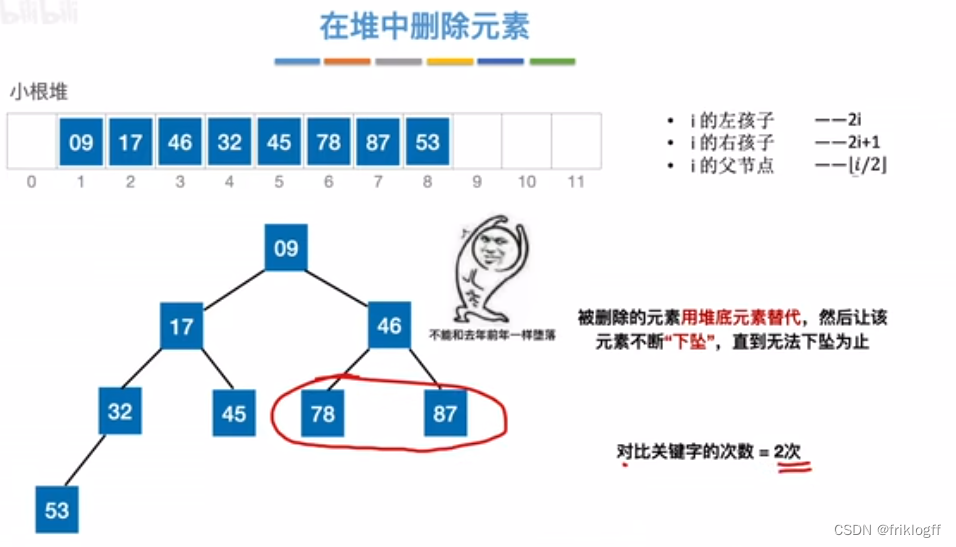
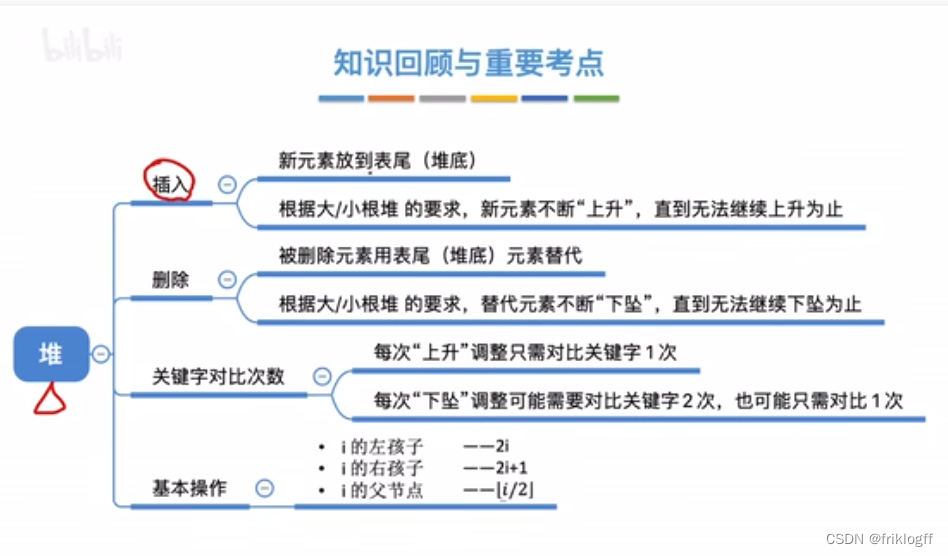
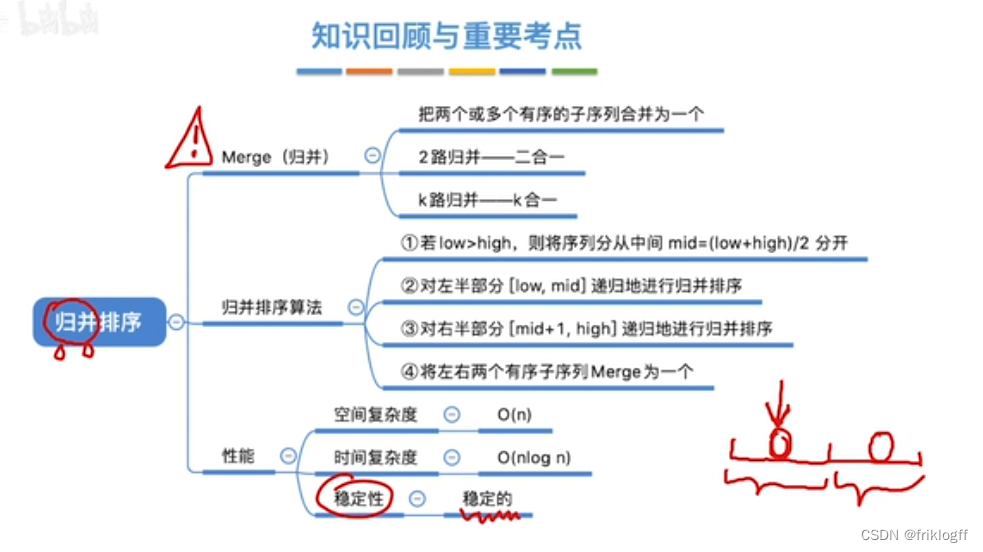
二路归并排序
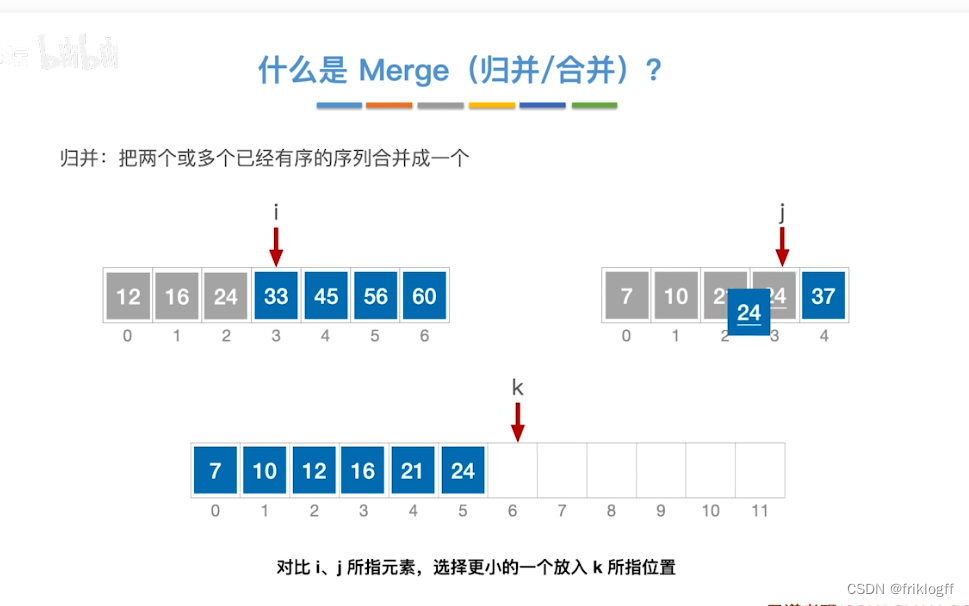
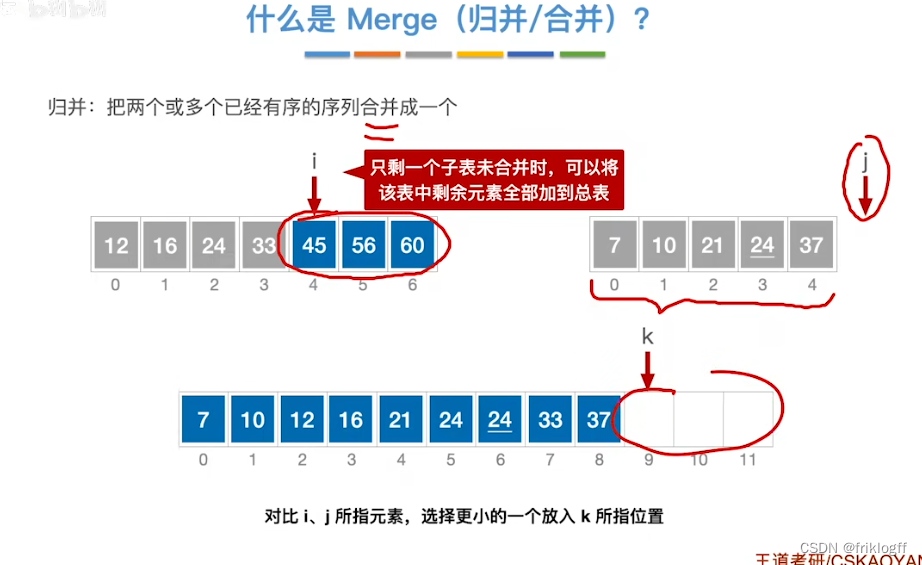
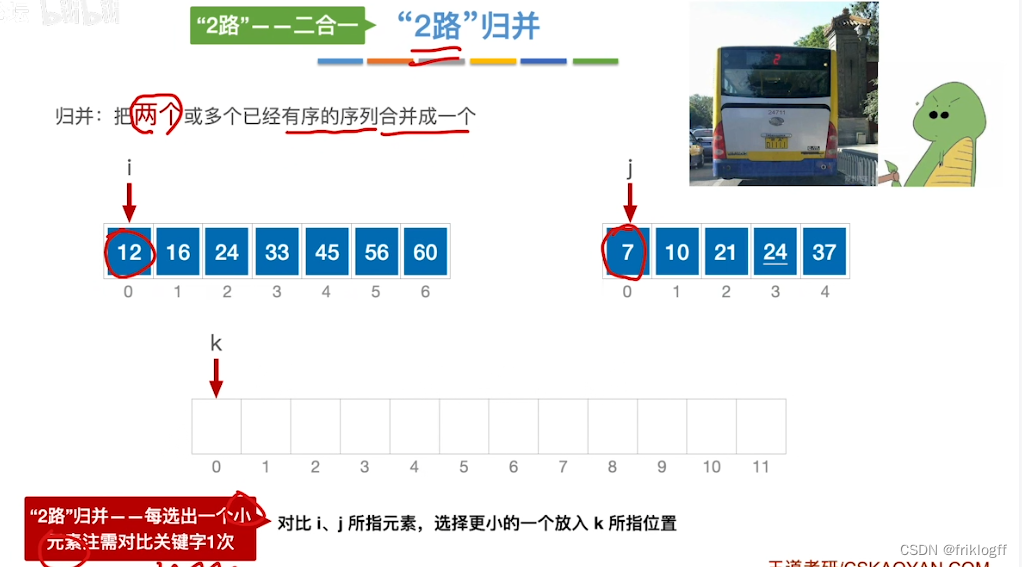
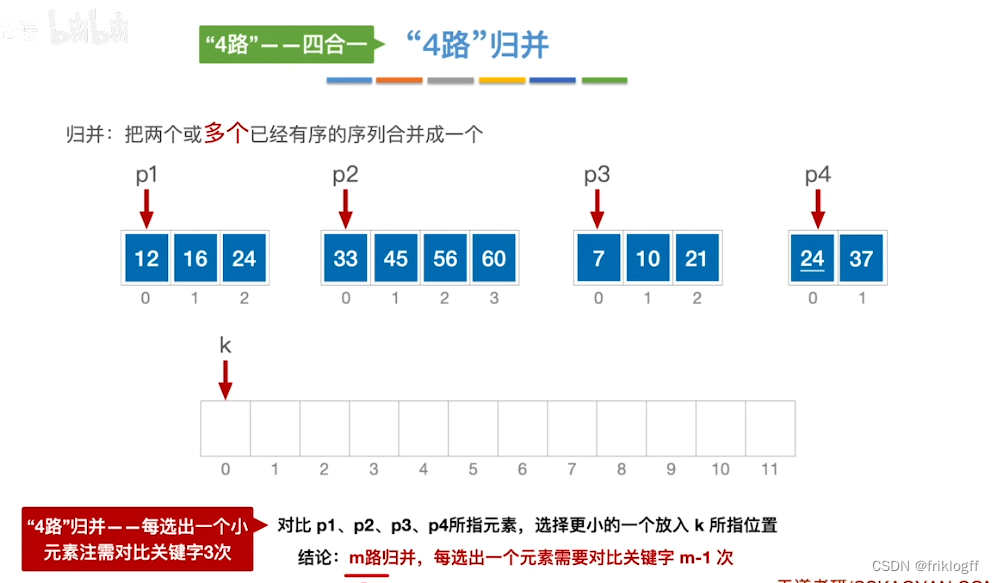
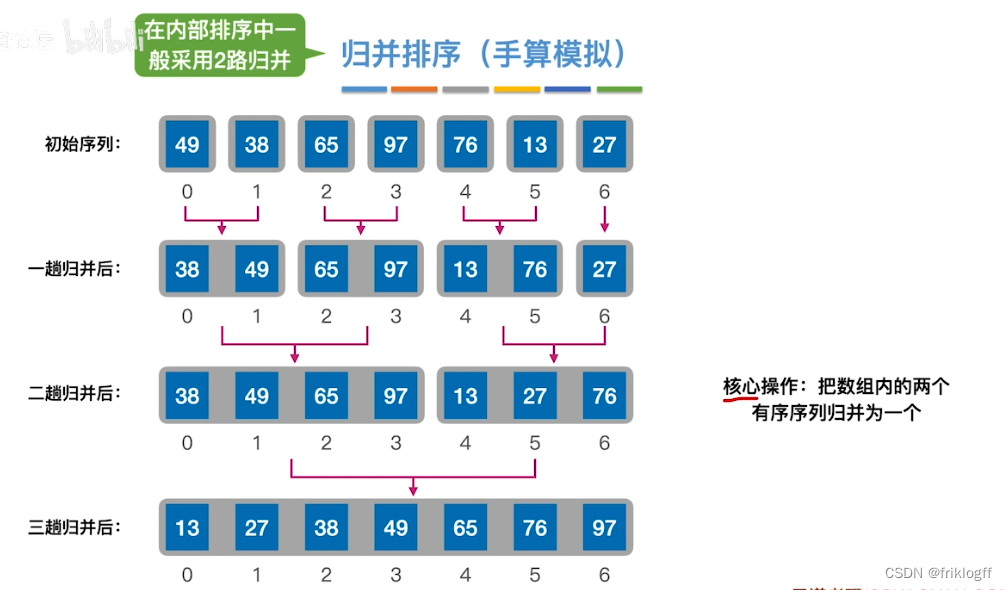
实现过程
-
假定待排序表有n个记录,可以看成n个有序子表,每个子表长度1,两两归并,得到⌈n/2⌉个长度为2或1的有序表,再两两归并,直到合并为长度n的有序表
-
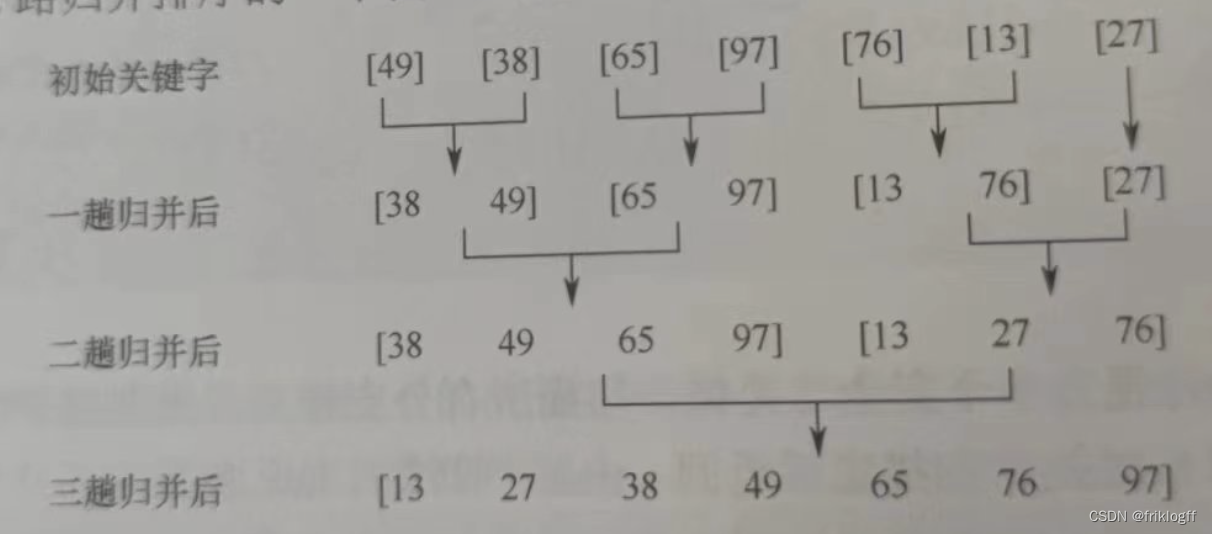
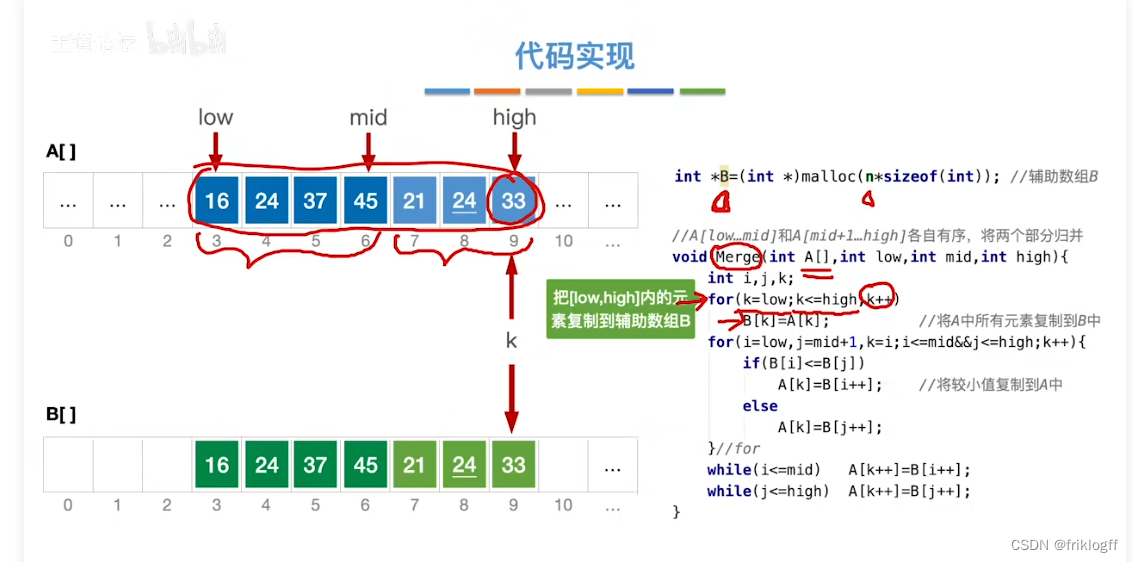
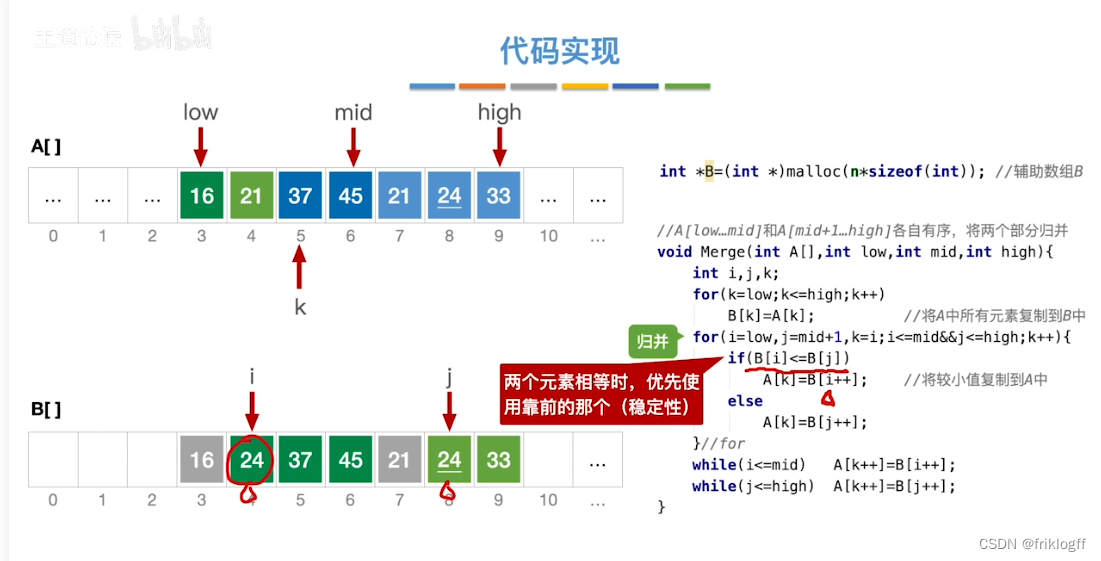
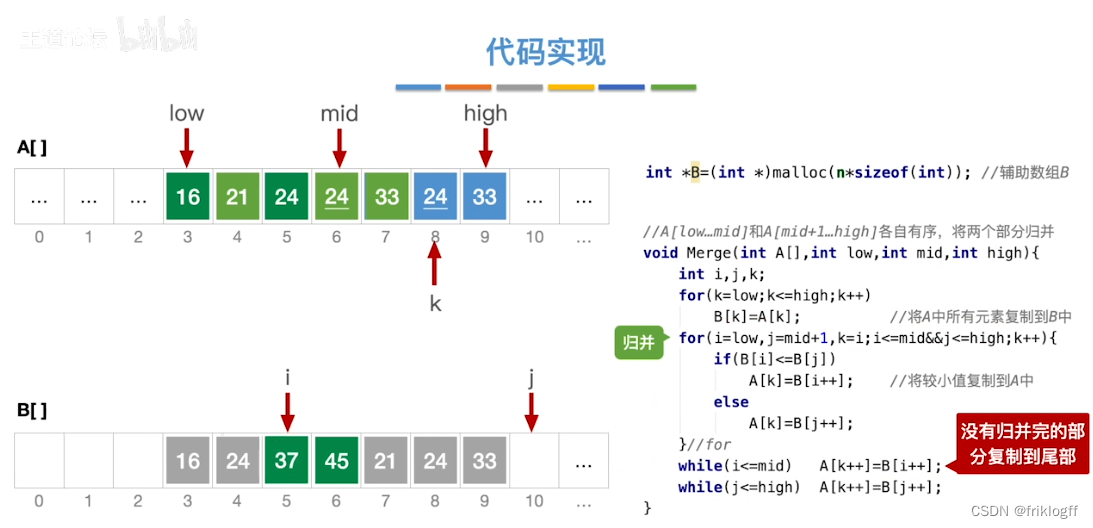

-
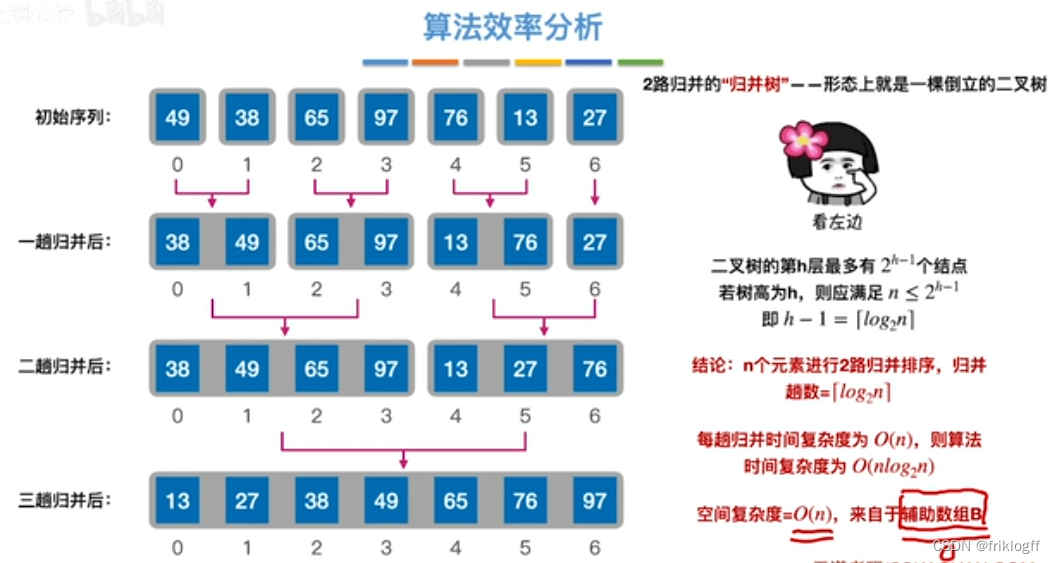
性能分析
-
时间复杂度:O(nlog2n)
-
空间复杂度:O(n)
-
-
稳定性
- 稳定
-
特点
-
比较次数与初始状态无关
-
只有归并排序O(nlog2n)且稳定
-
-
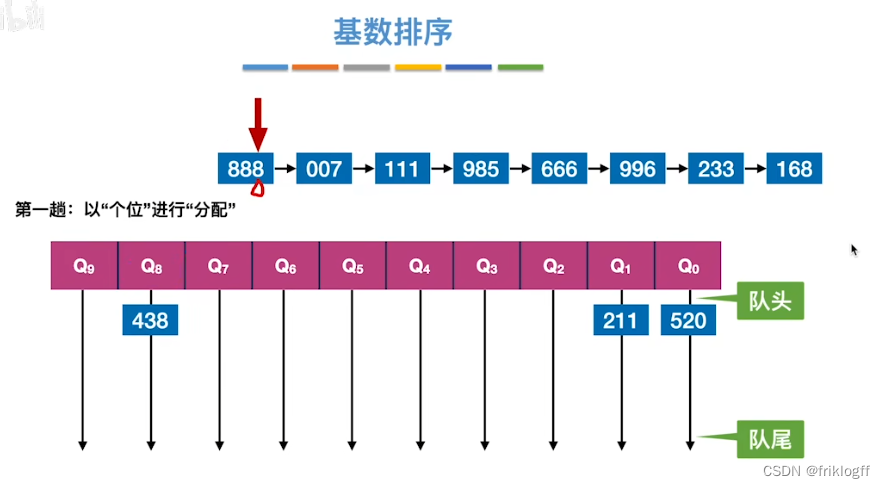
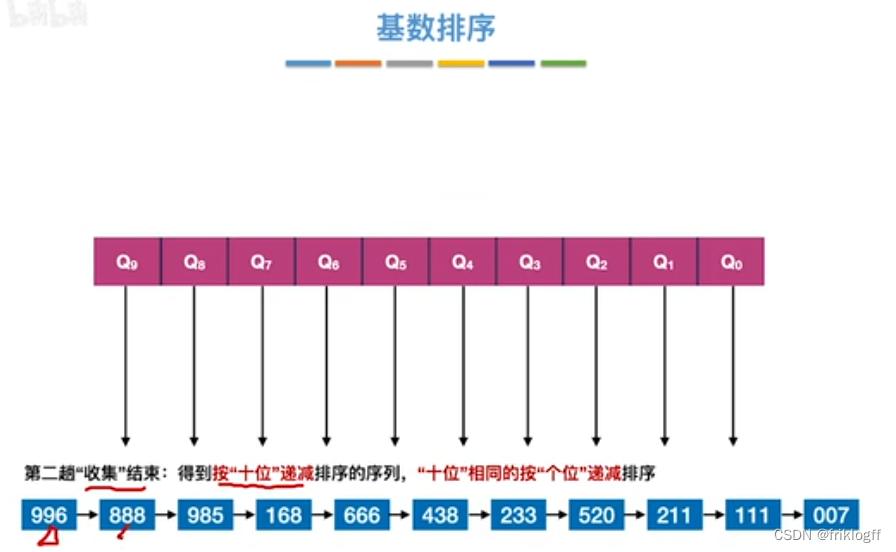
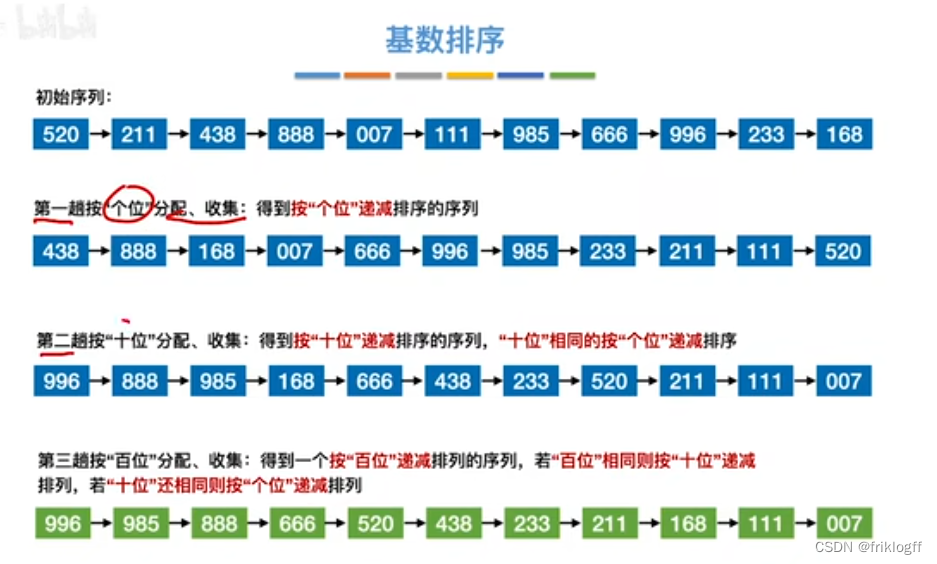
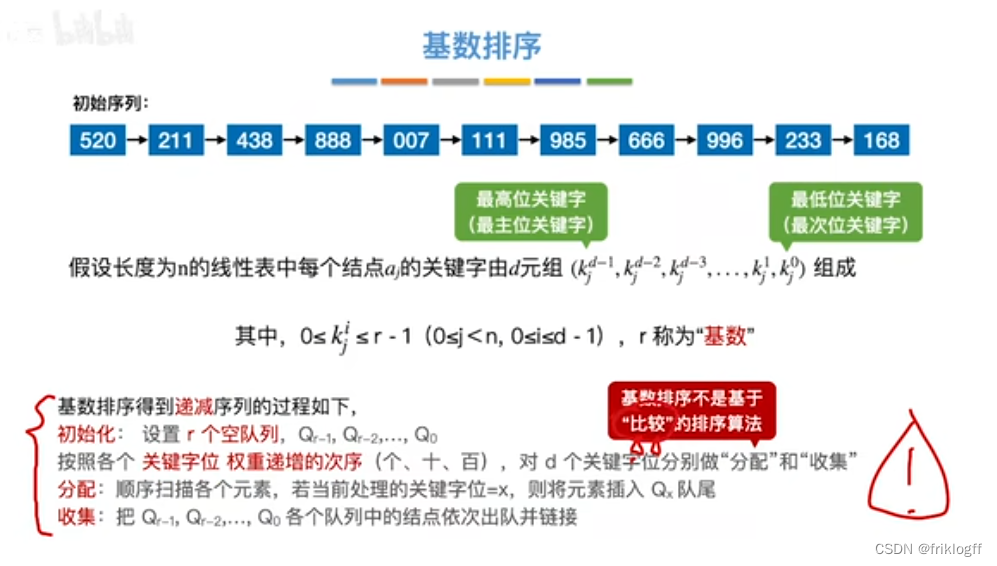
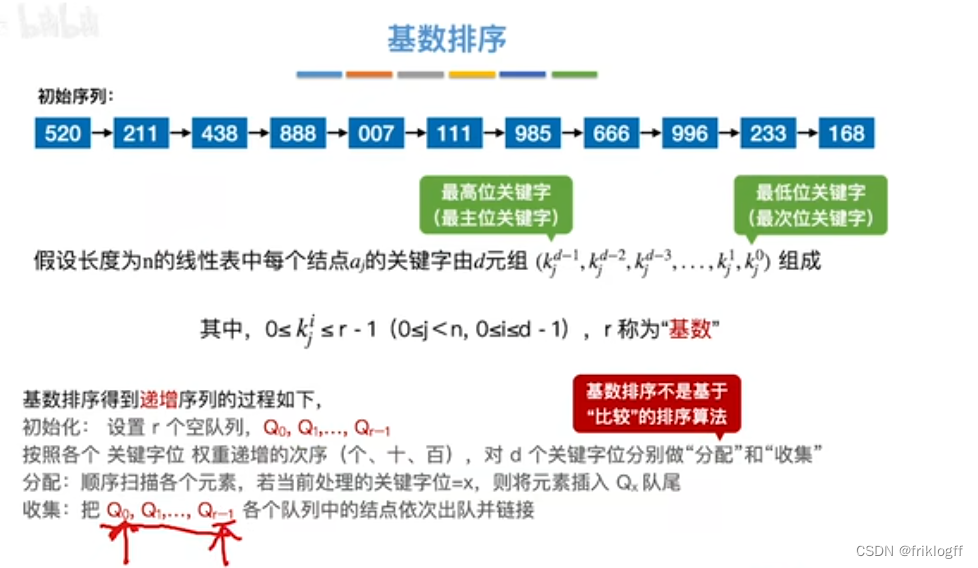
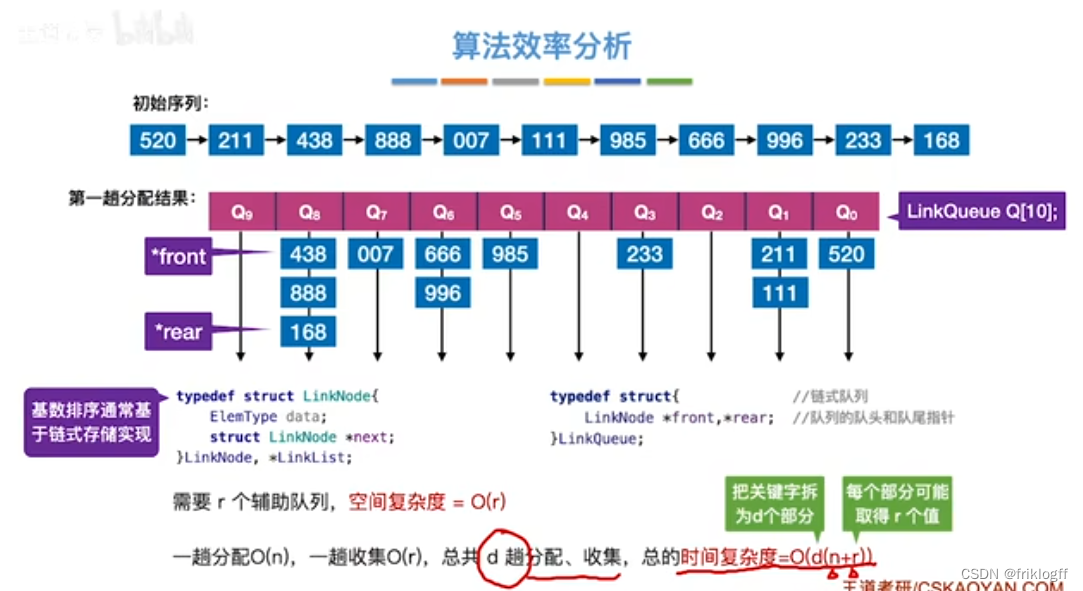
基数排序
基本概念
-
最高位优先(MSD)法:按关键字位权重递减依次逐层划分成若干更小的子序列,最后将所有子序列依次连接成一个有序序列
-
最低位优先(LSD)法:按关键字位权重递增依次进行排序,最后形成一个有序序列
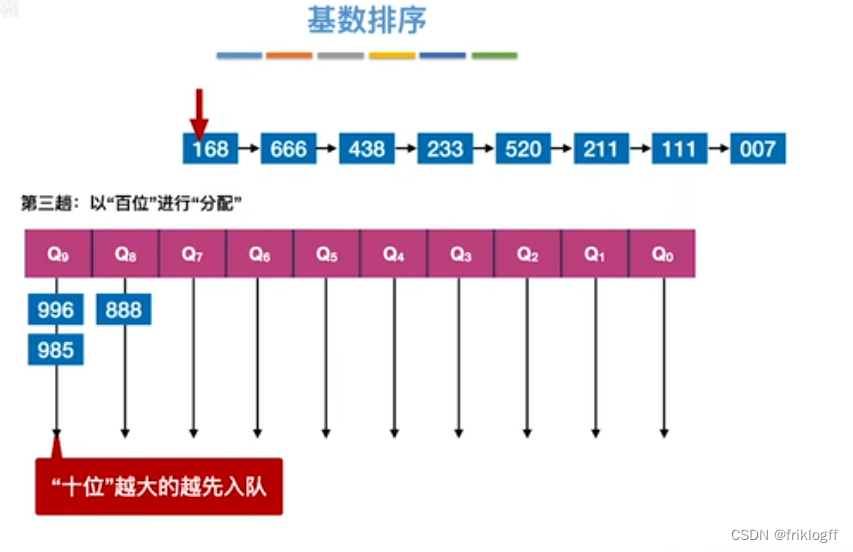
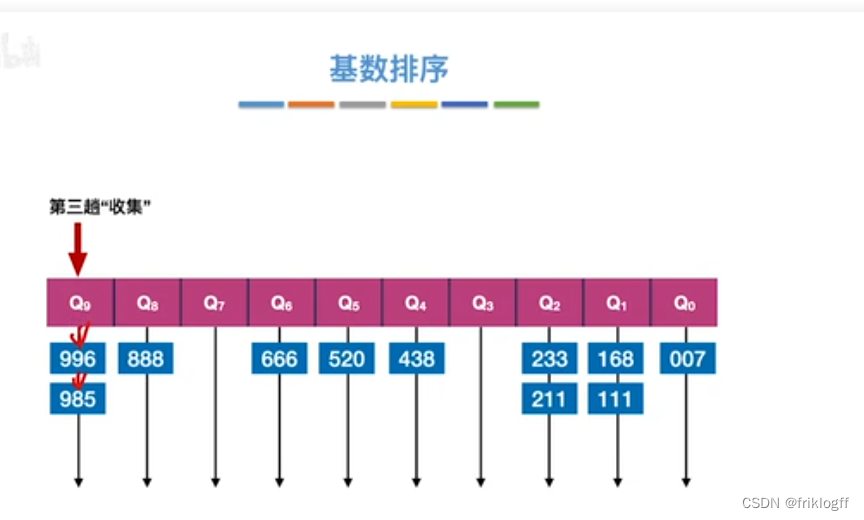
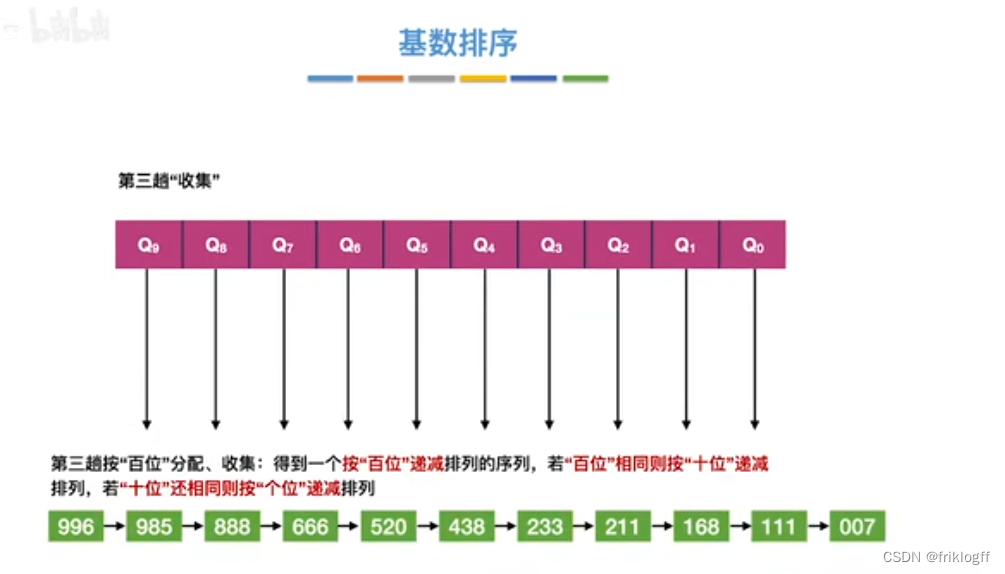
实现过程
- 采用多关键字排序思想(即基于关键字各位的大小进行排序的),借助“分配”和“收集”两种操作对单逻辑关键字进行排序,直到所有关键字均已排序完毕
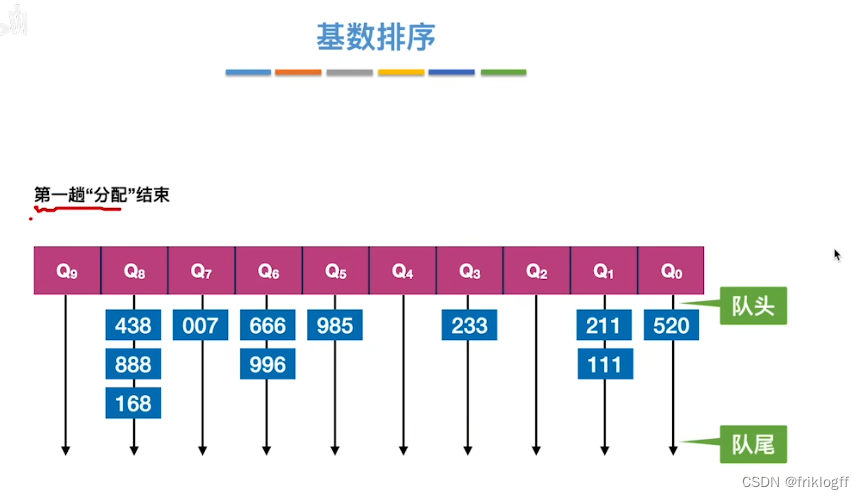
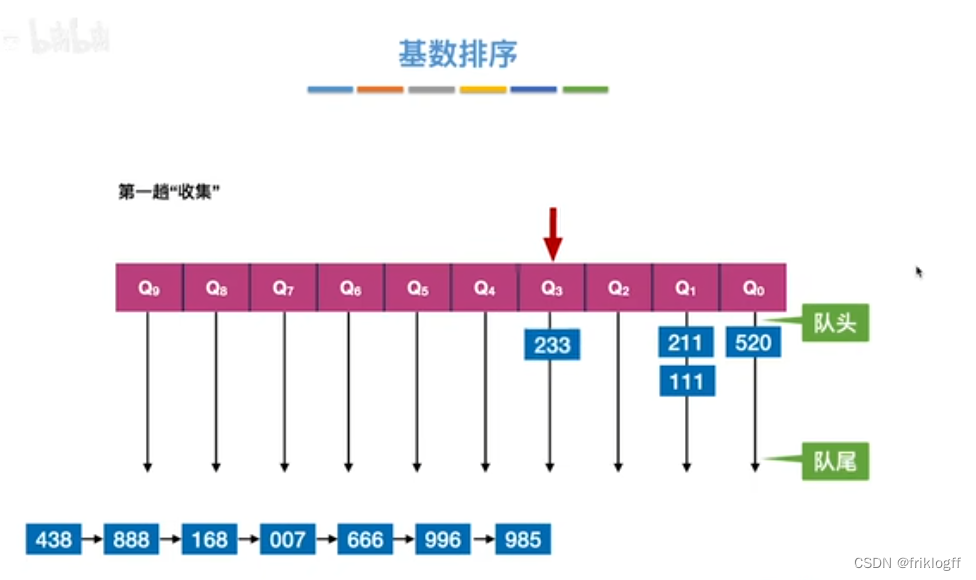
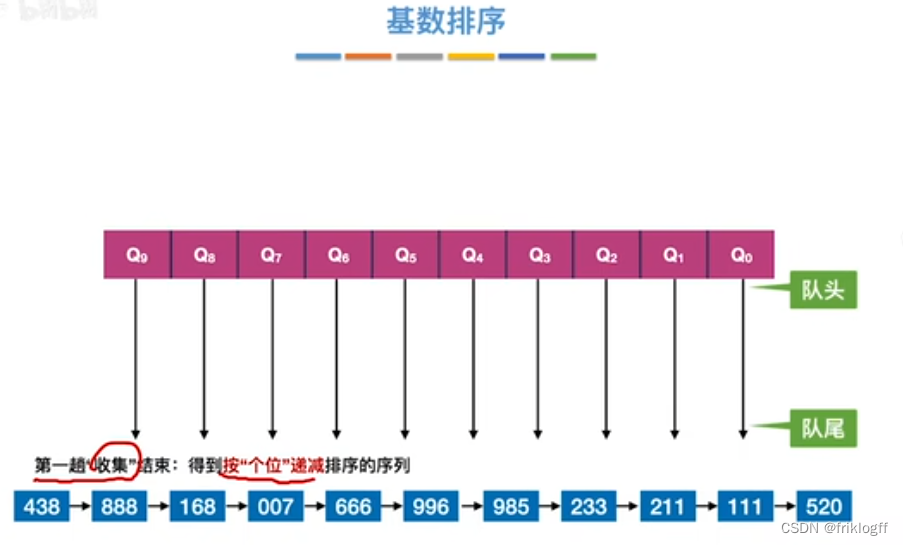

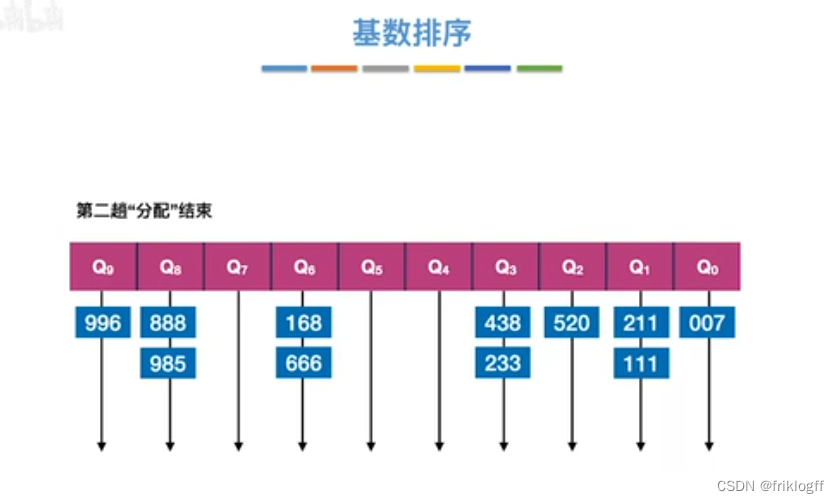
性能分析
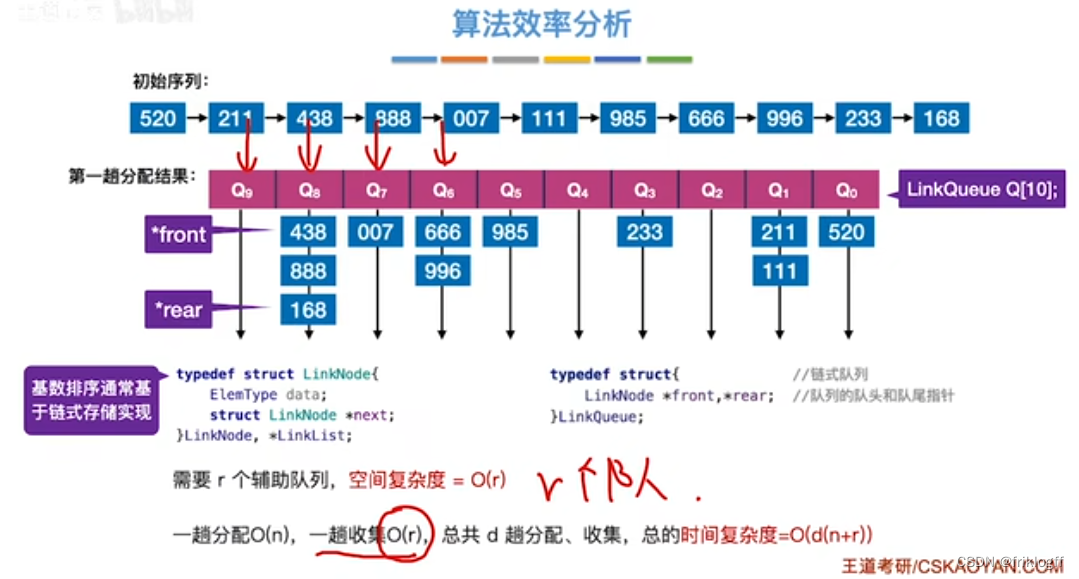
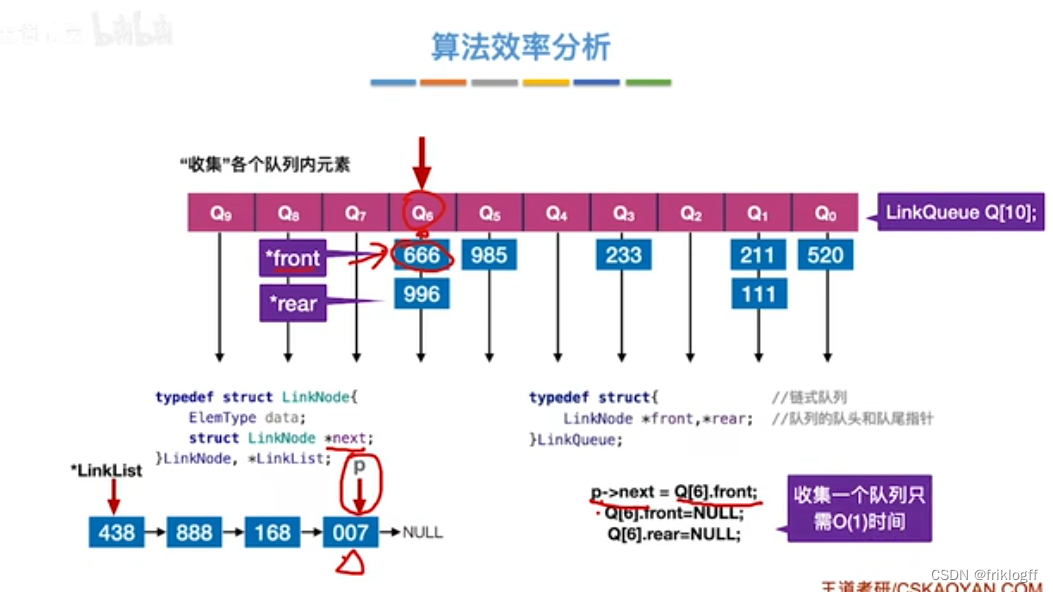
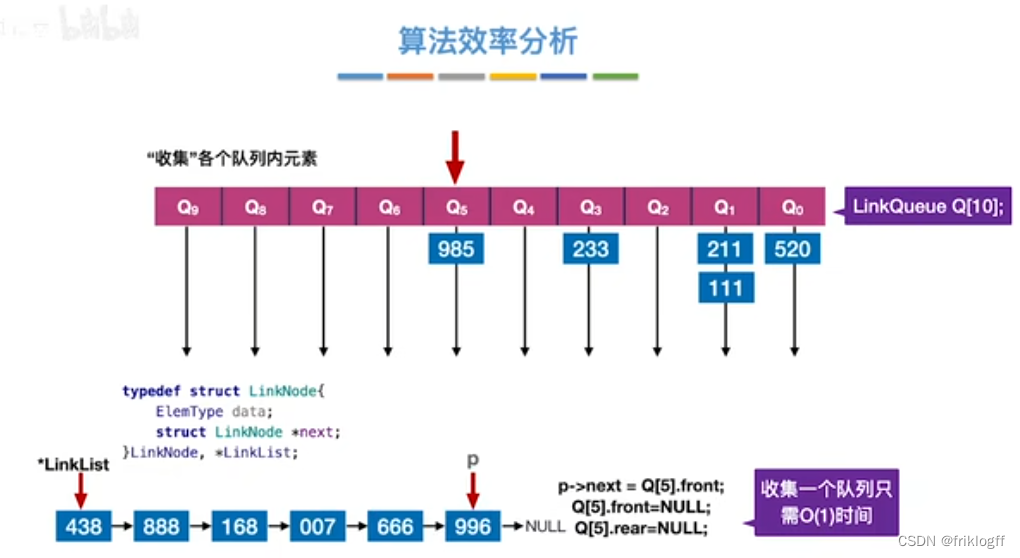
-
时间复杂度
- 基数排序需要进行k躺分配和收集,一趟分配需要O(n),一趟收集需要O(m),所以时间复杂度为O(k(n+m))
-
空间复杂度
-
链式存储(王道):O(m),一趟需要辅助存储空间m(m个桶的头尾指针)
-
顺序存储:O(n+m),桶+临时存放数组
-
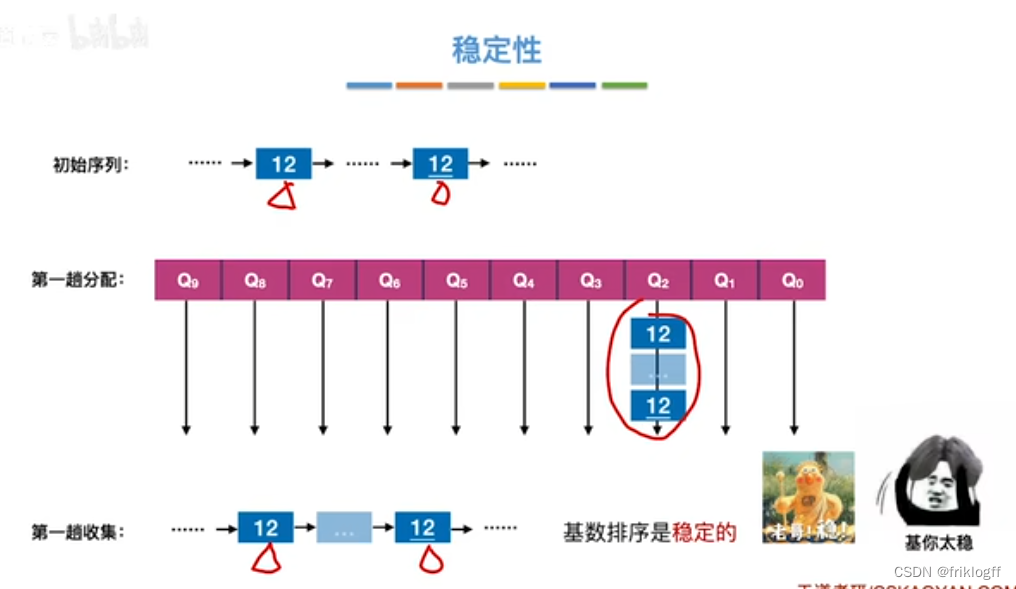
稳定性
- 稳定
应用
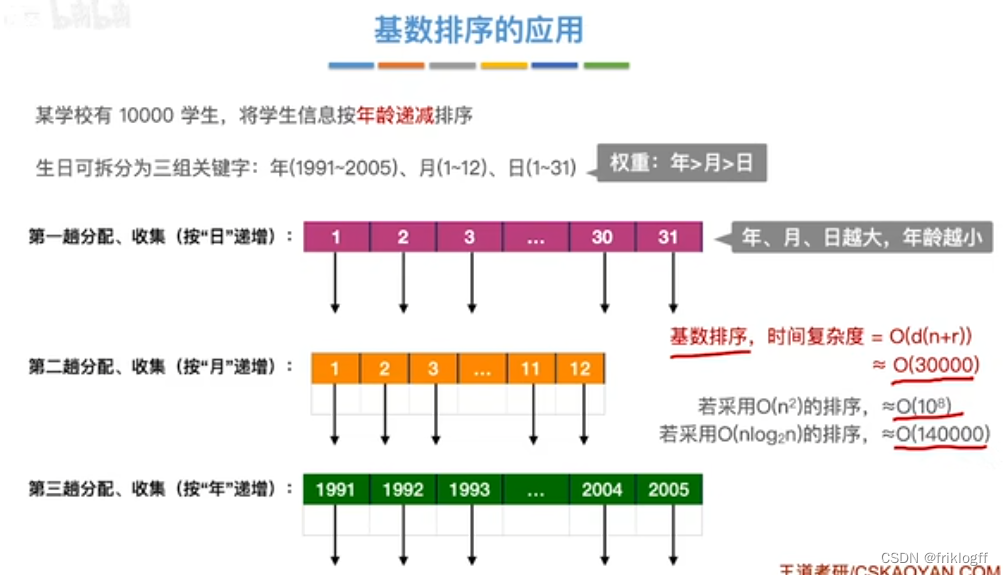

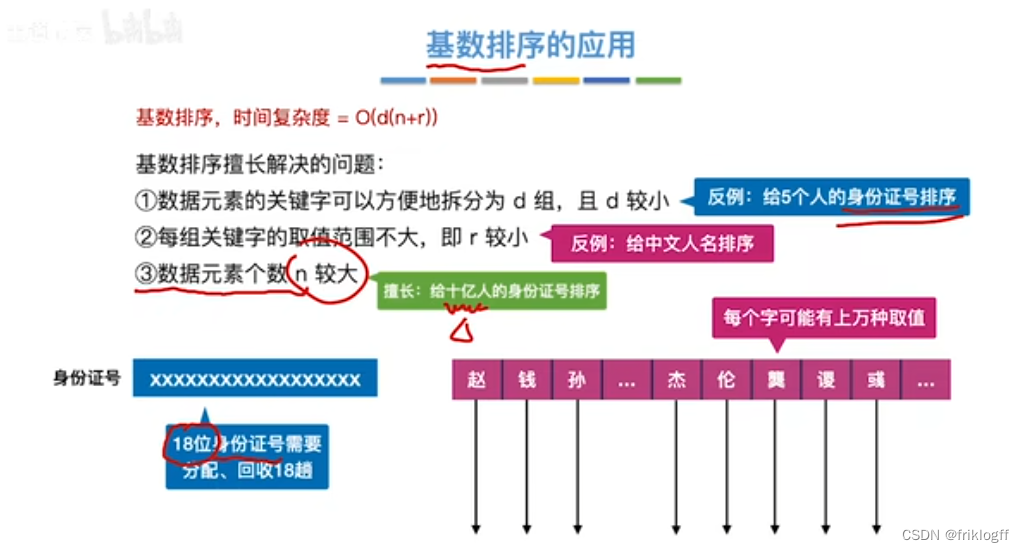
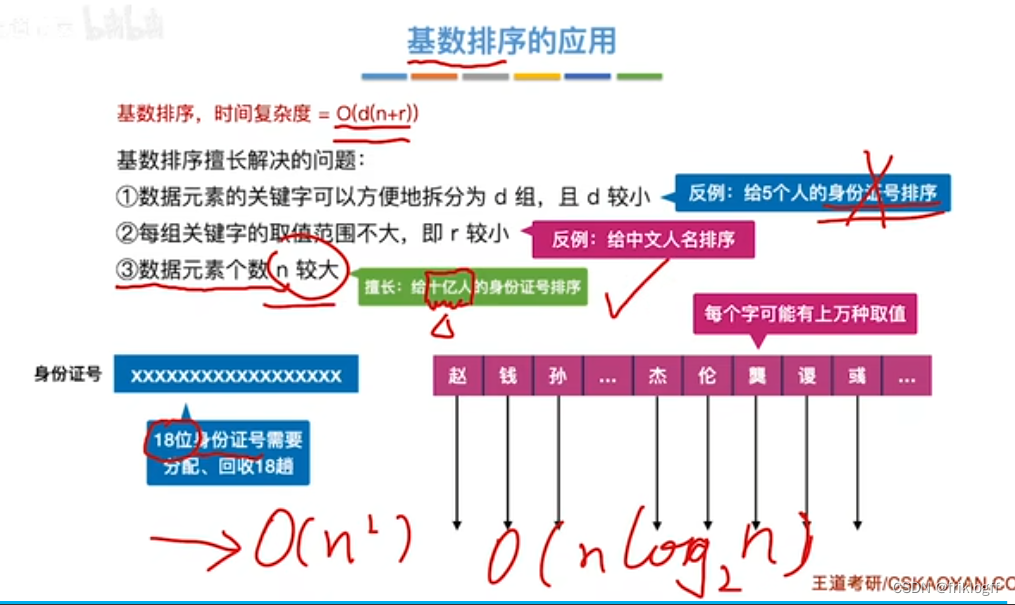

-
关键字便于分k组,即k较小时
-
每组关键字取值范围不大,即m较少时
-
元素个数n较大时
补充
- 对数字排序时,仅能使用最低位优先法,若高位优先,最后排低位时会打乱顺序
排序算法的分析
-
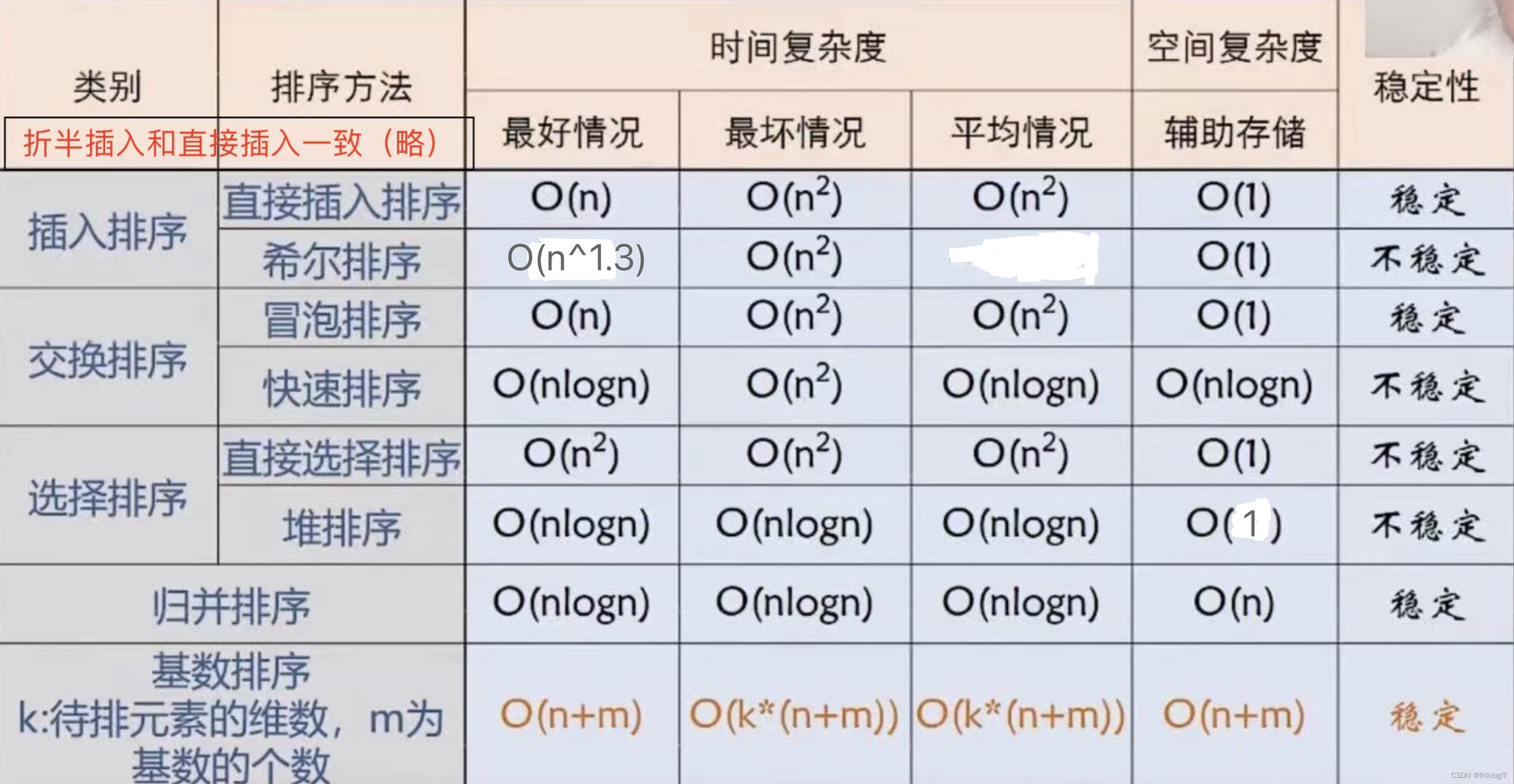
-
王道书中基数排序,d为待排元素的维度,r为基数的个数,空间复杂度王道采用链式存储,故额外空间仅每个桶的头尾指针
结论
-
若文件初始状态接近有序,则选用直接排序或冒泡排序为宜
-
要求排序稳定且时间复杂度O(nlog2n),则选用归并排序
-
若n很大,记录关键字位数较少且可分解时,采用基数排序
-
当记录信息量较大,为避免消耗大量时间移动记录,可用链表作为存储结构
-
简单选择排序、堆排序、归并排序的时间性能不随记录序列中关键字的分布而改变
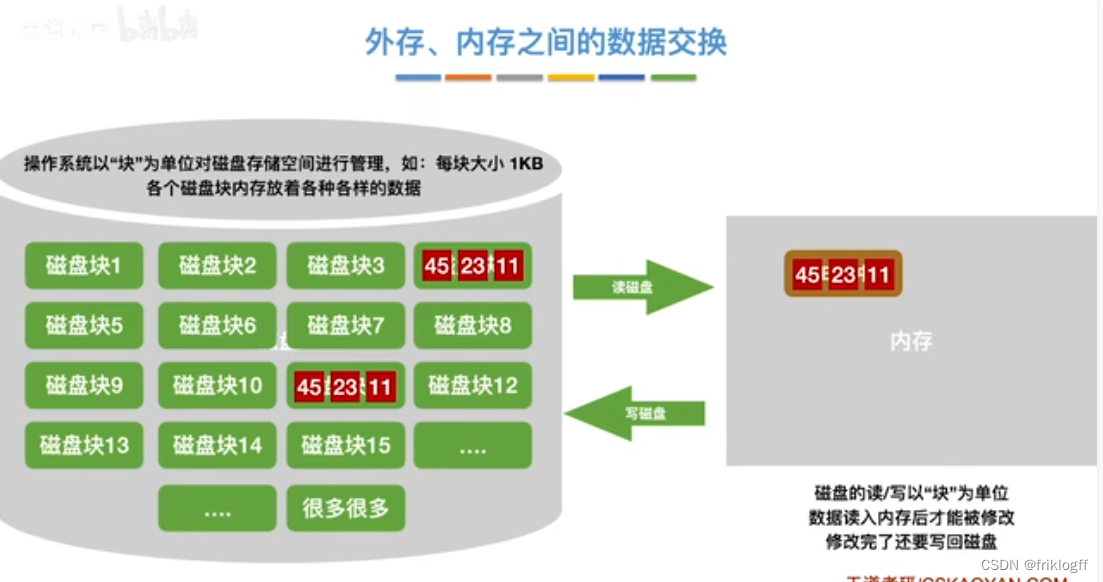
外部排序
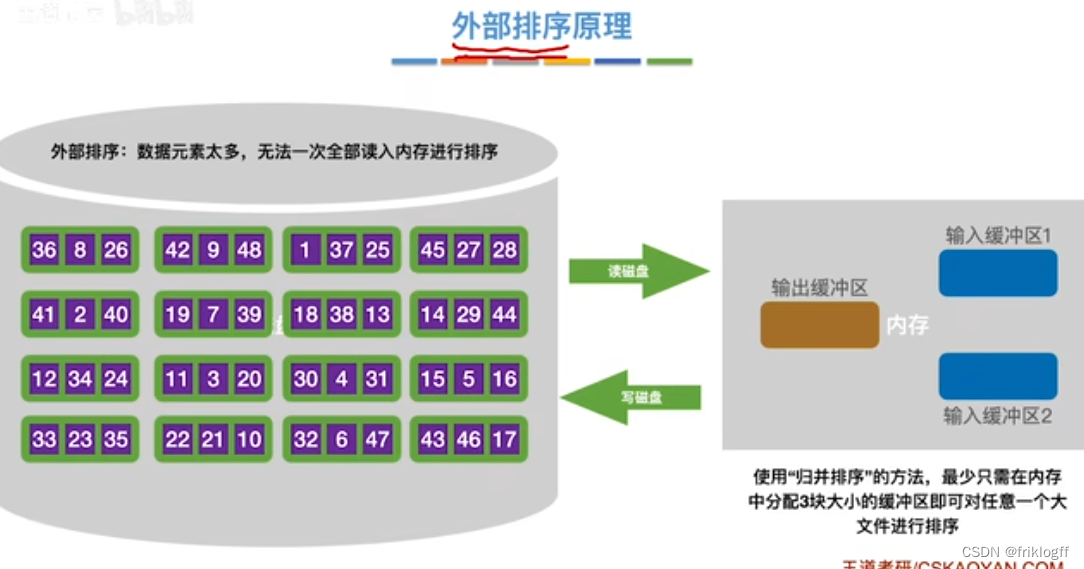
外部排序基本概念
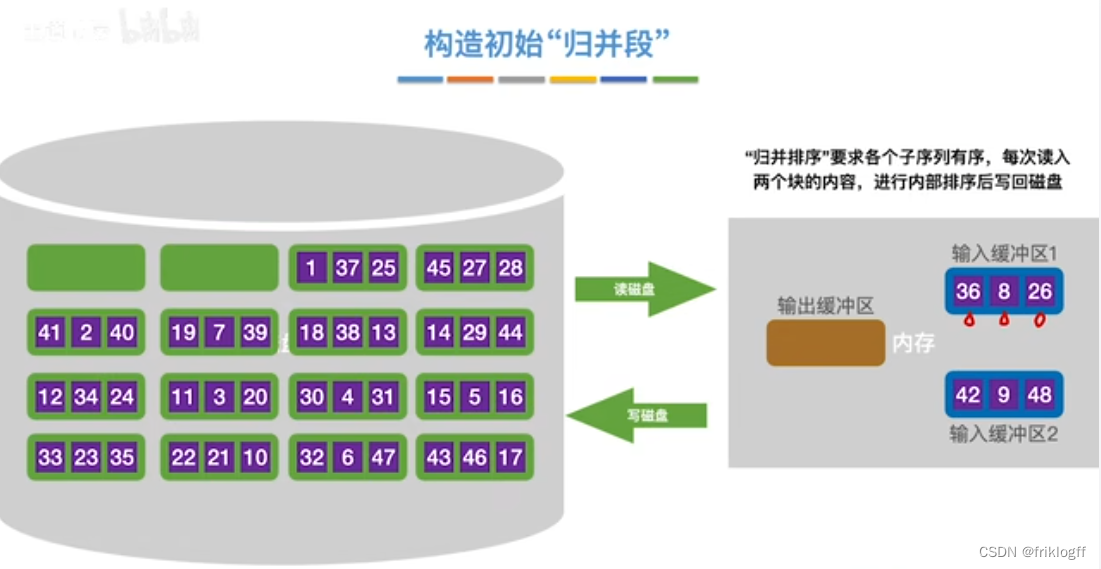
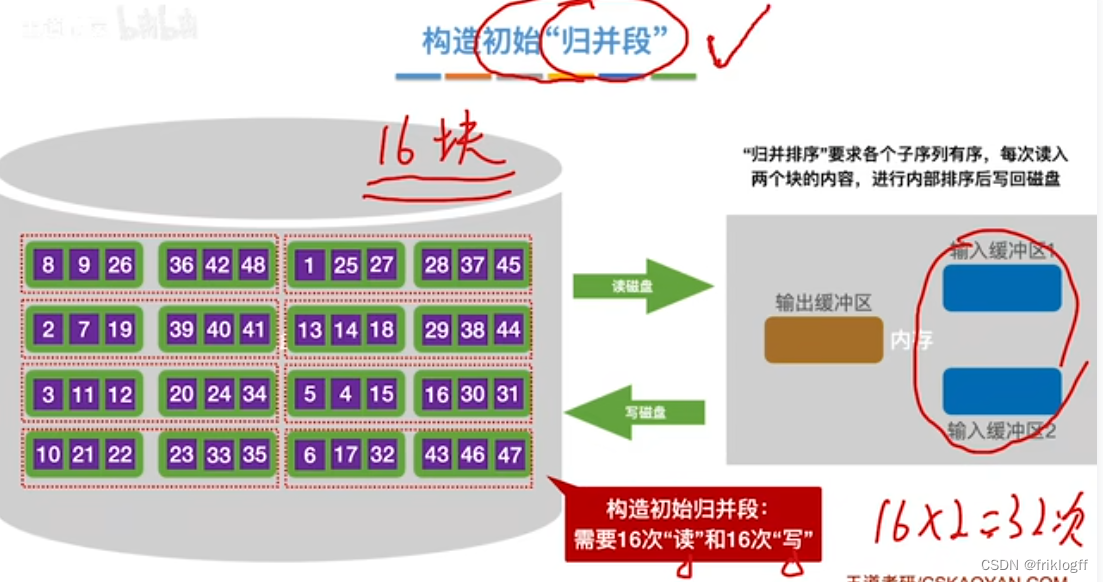
构造初始“归并段"
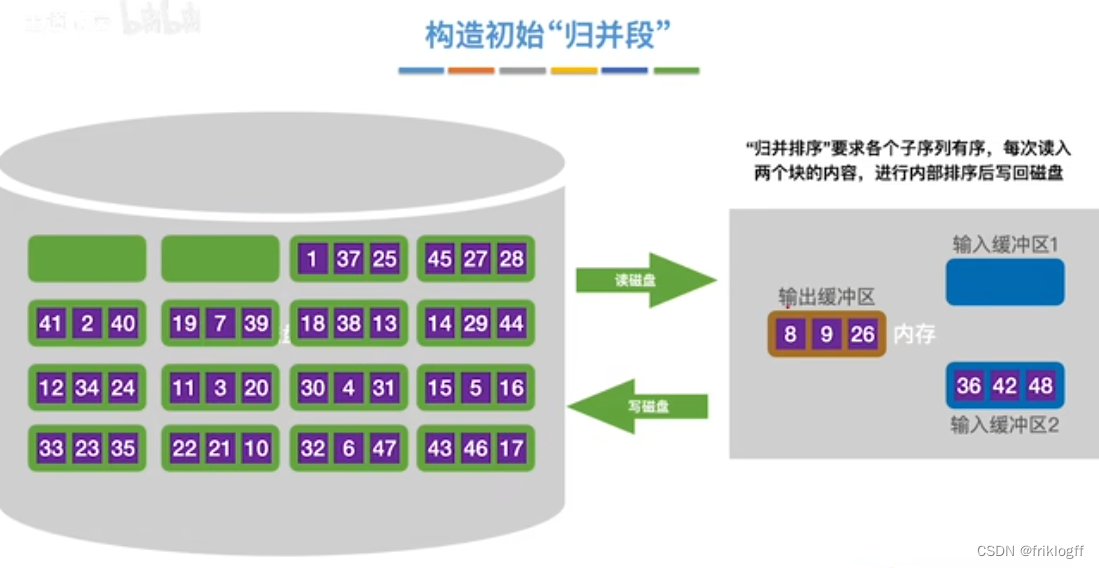
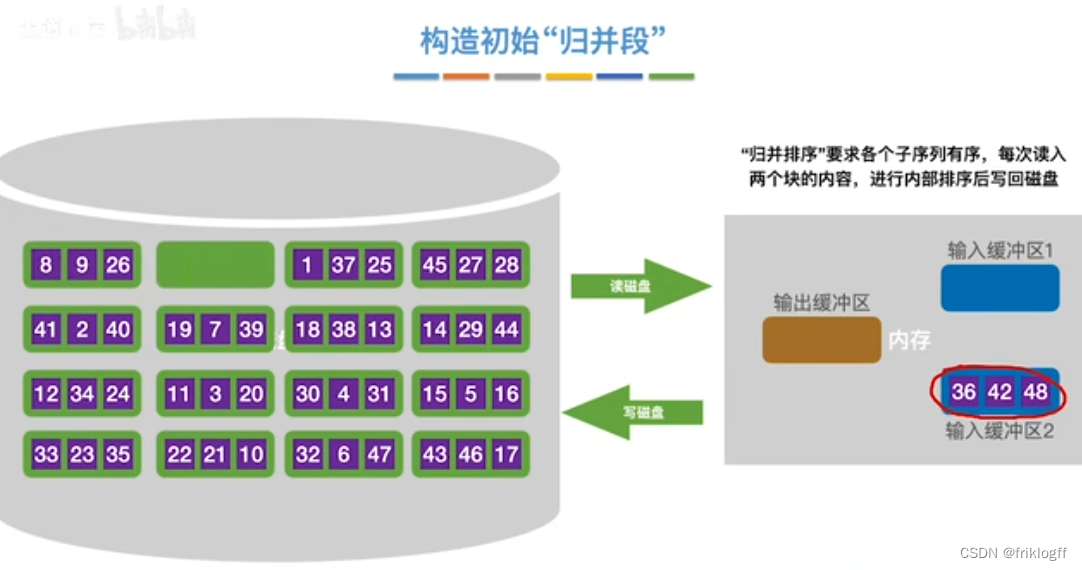
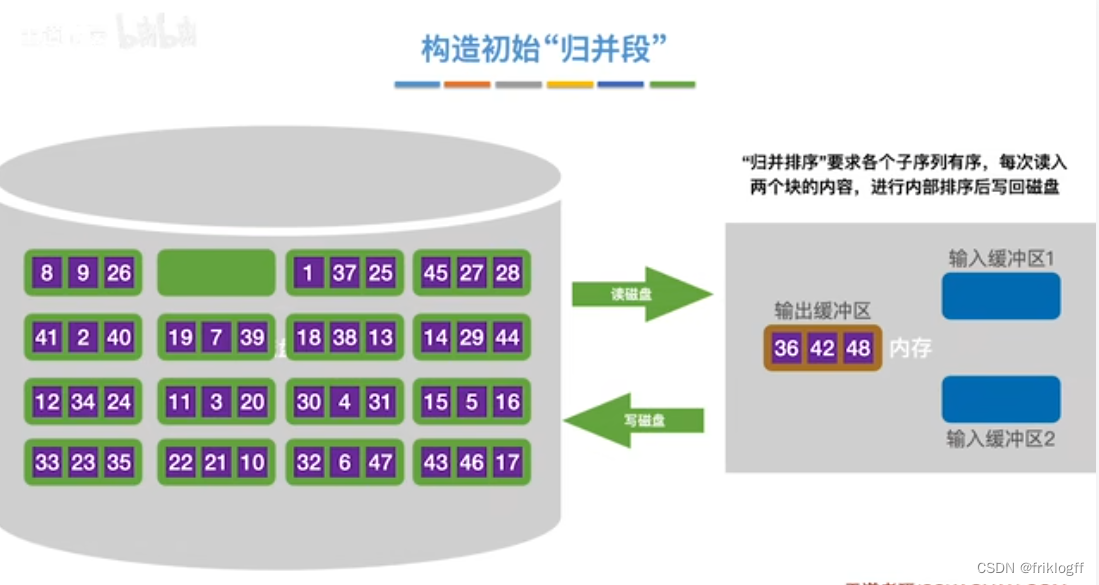
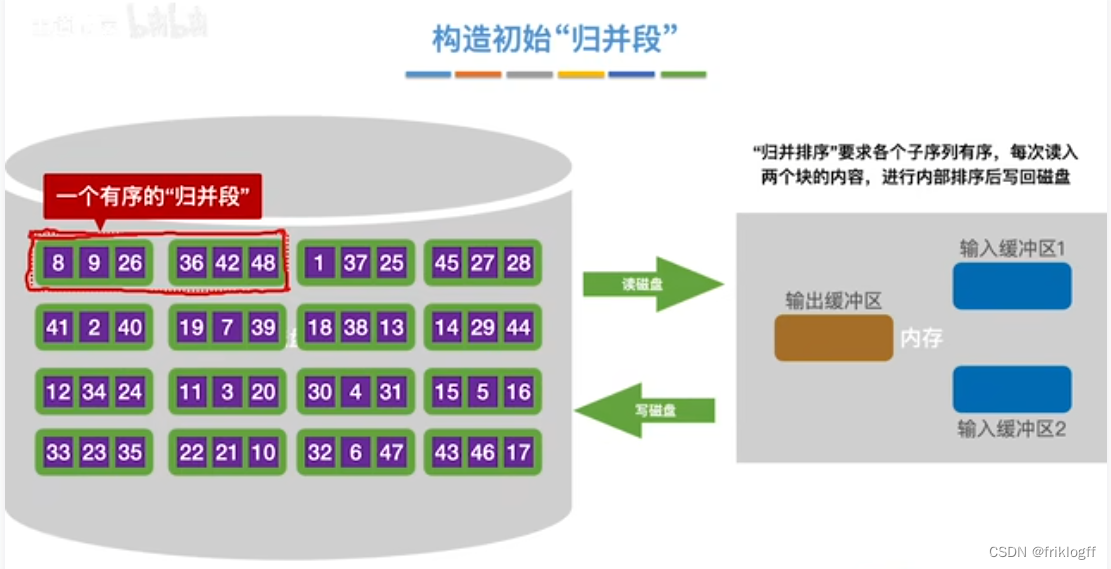
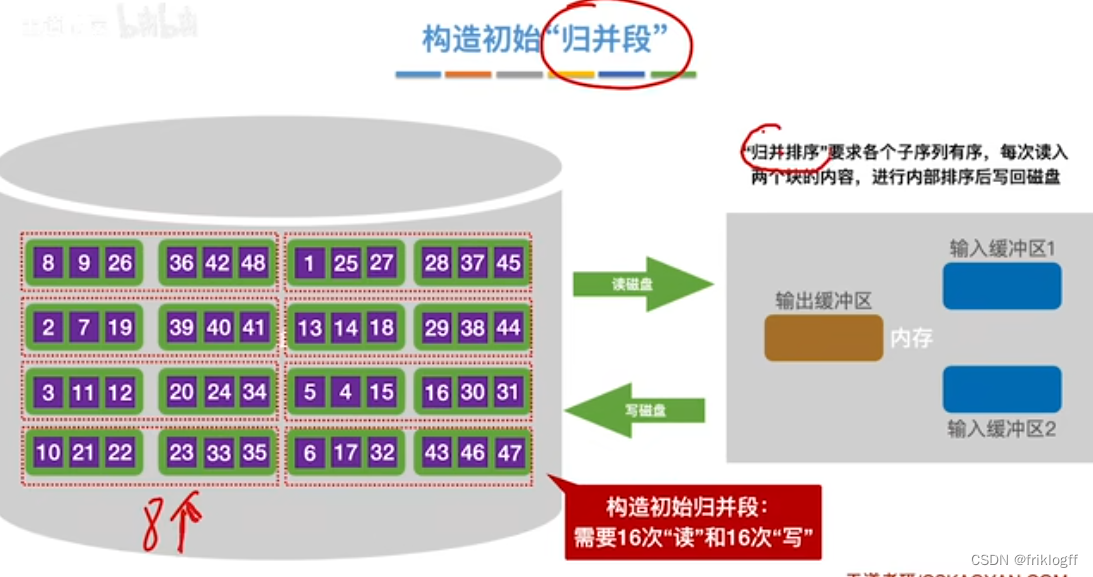
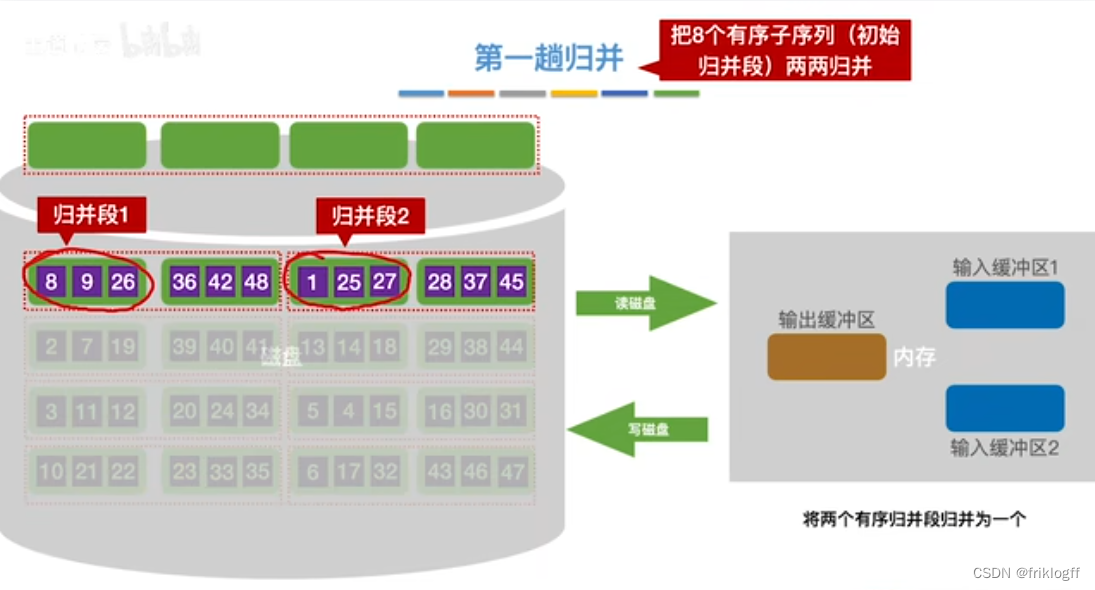
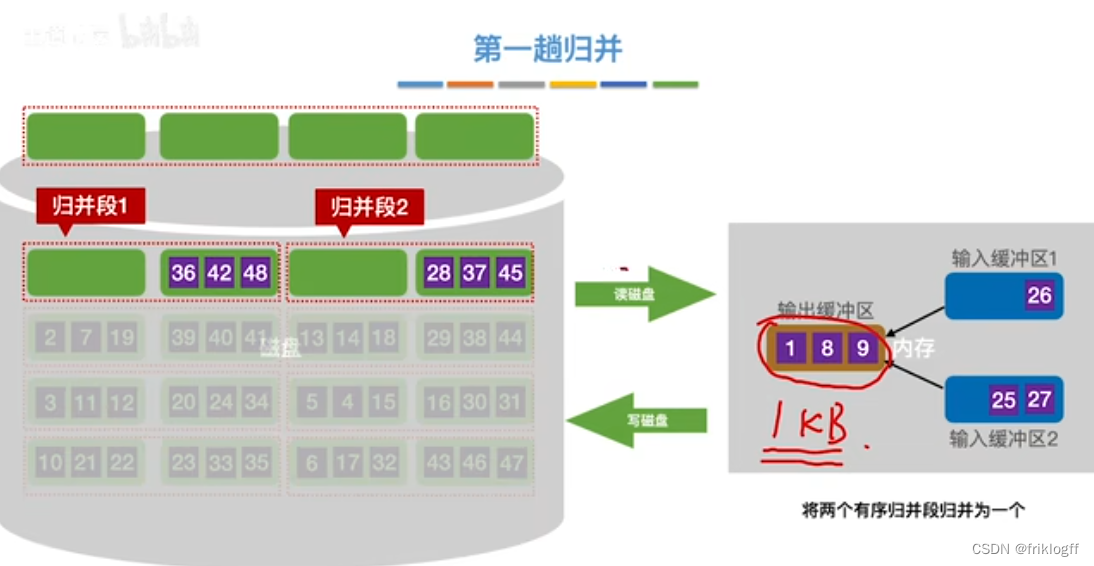
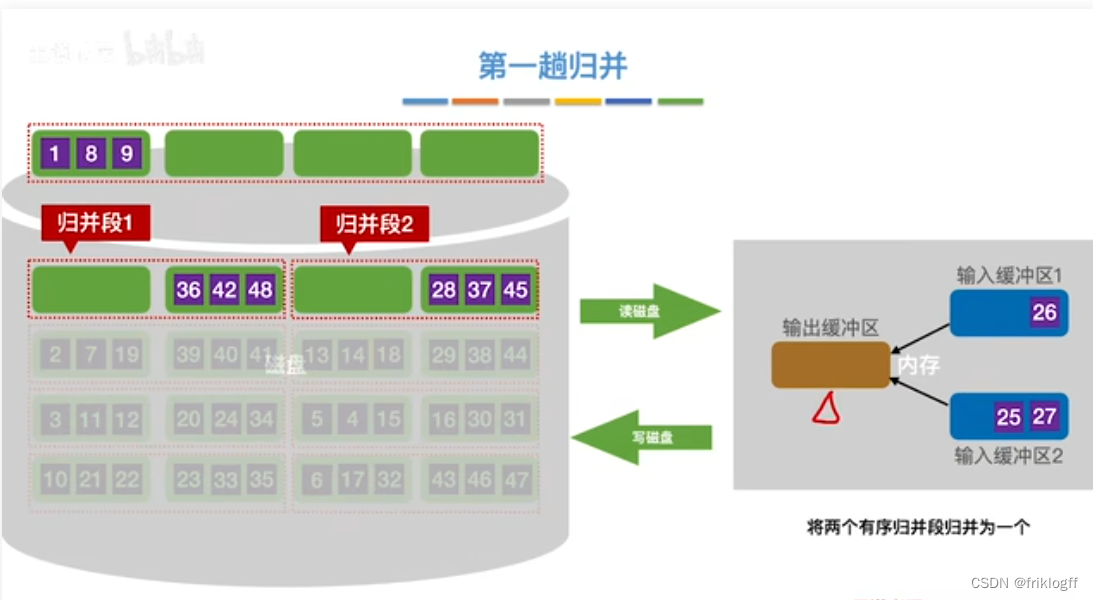
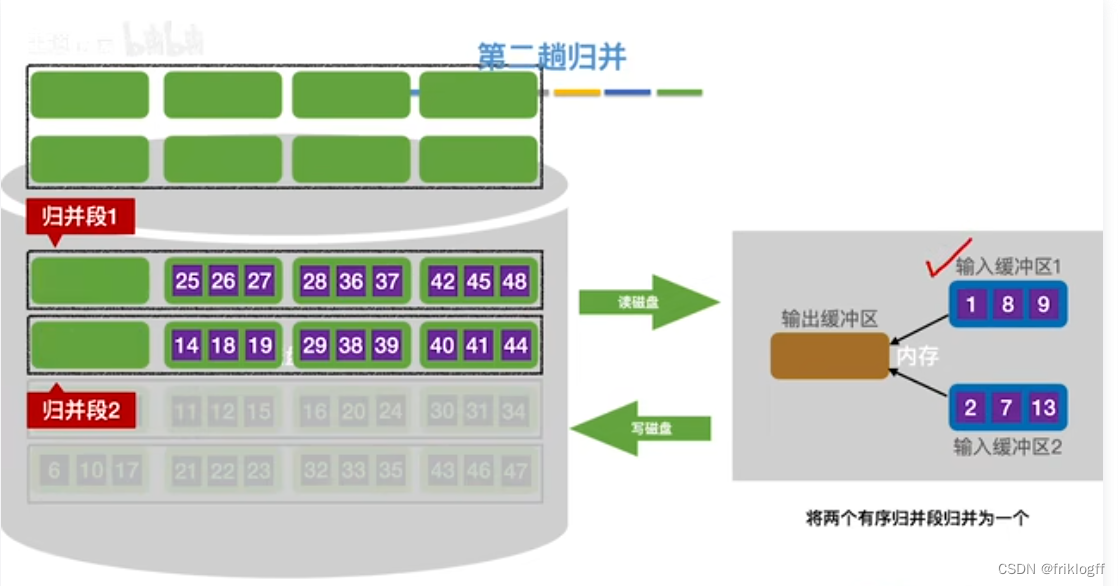
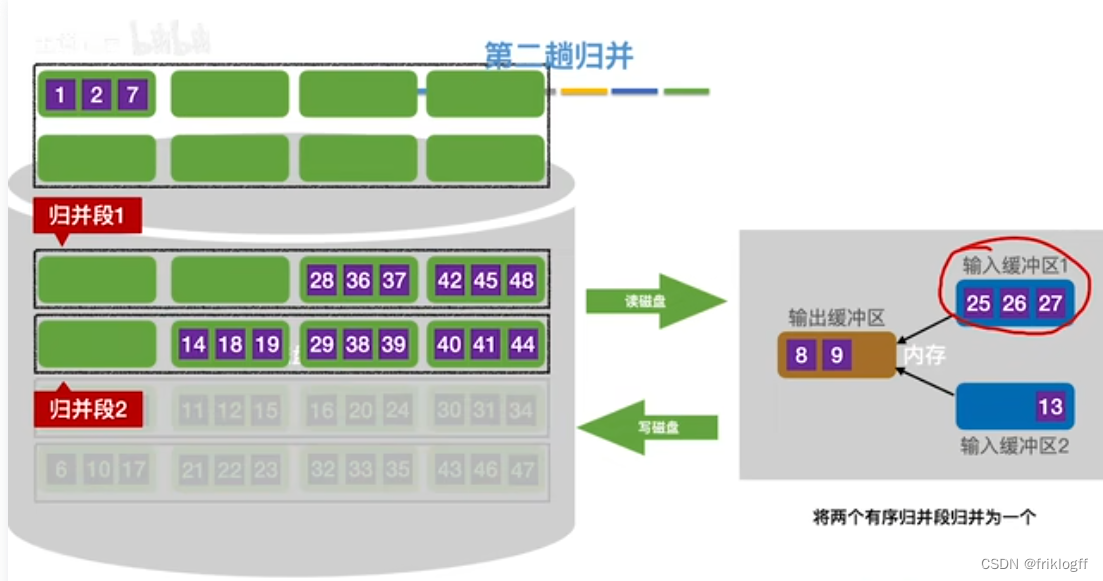
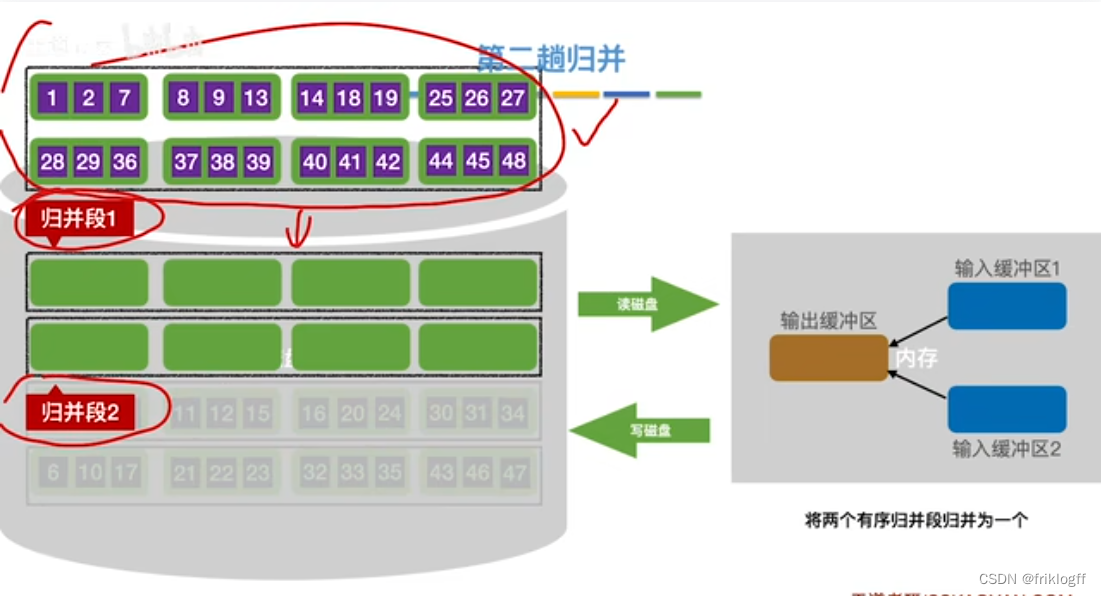
第一趟归并
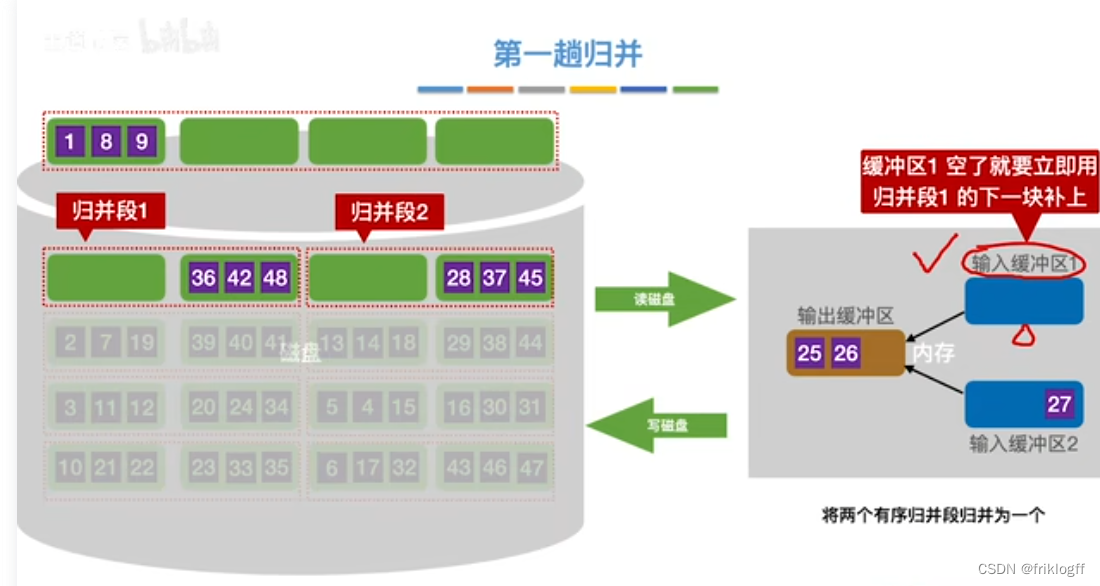
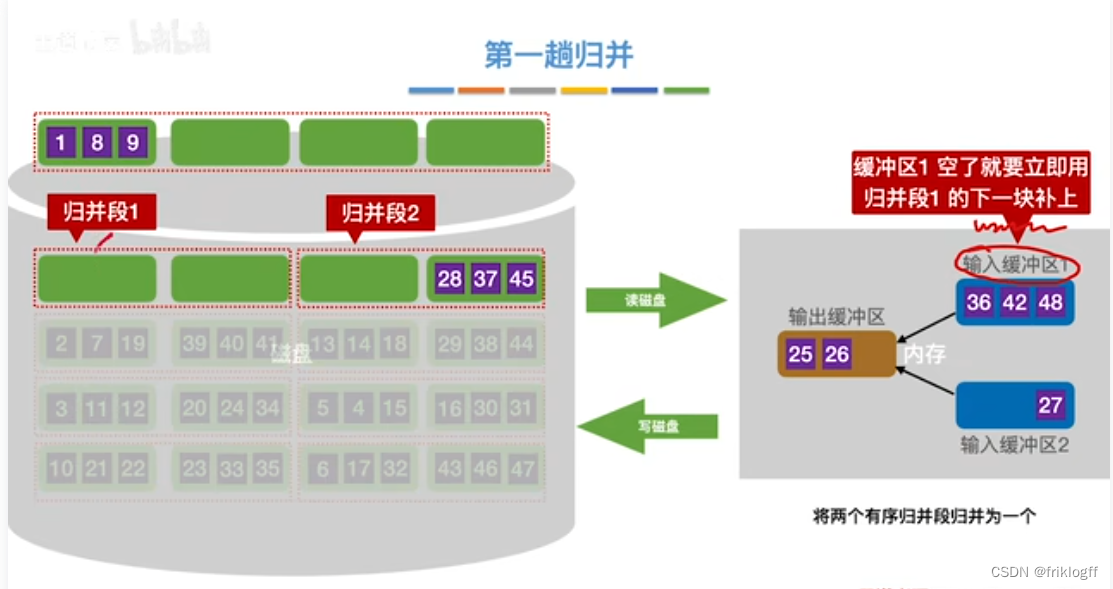
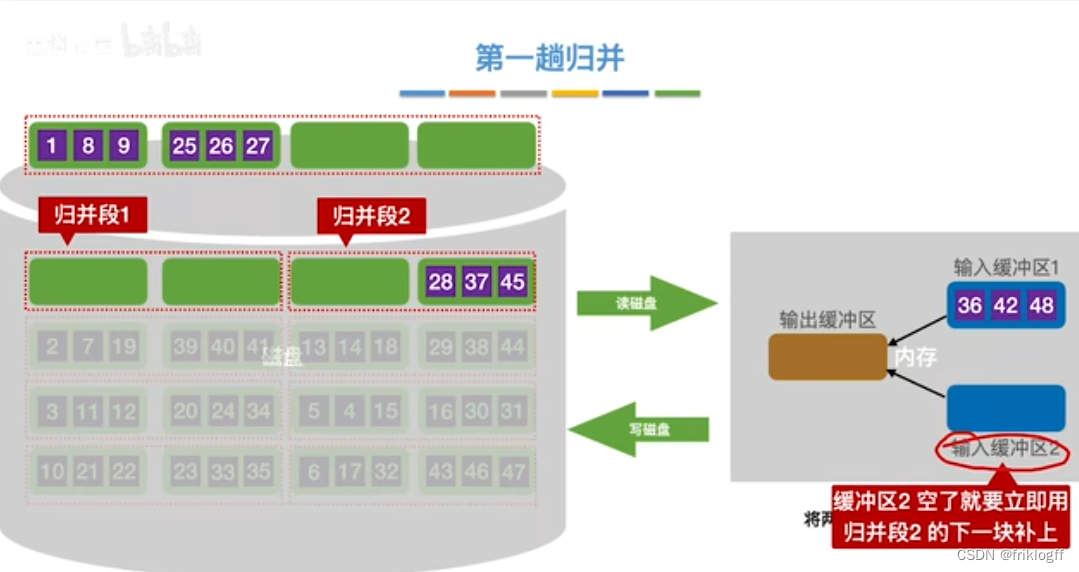
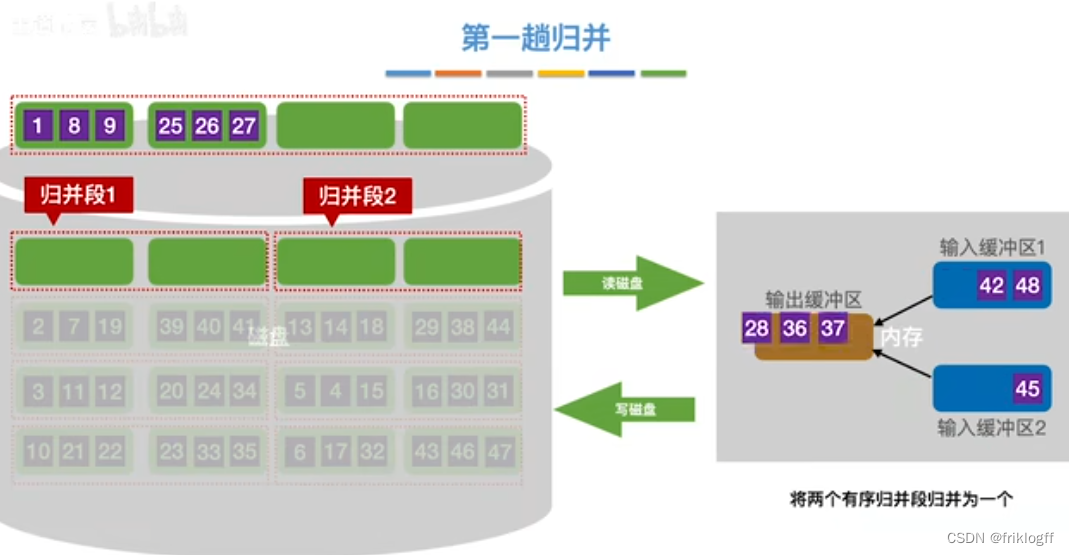
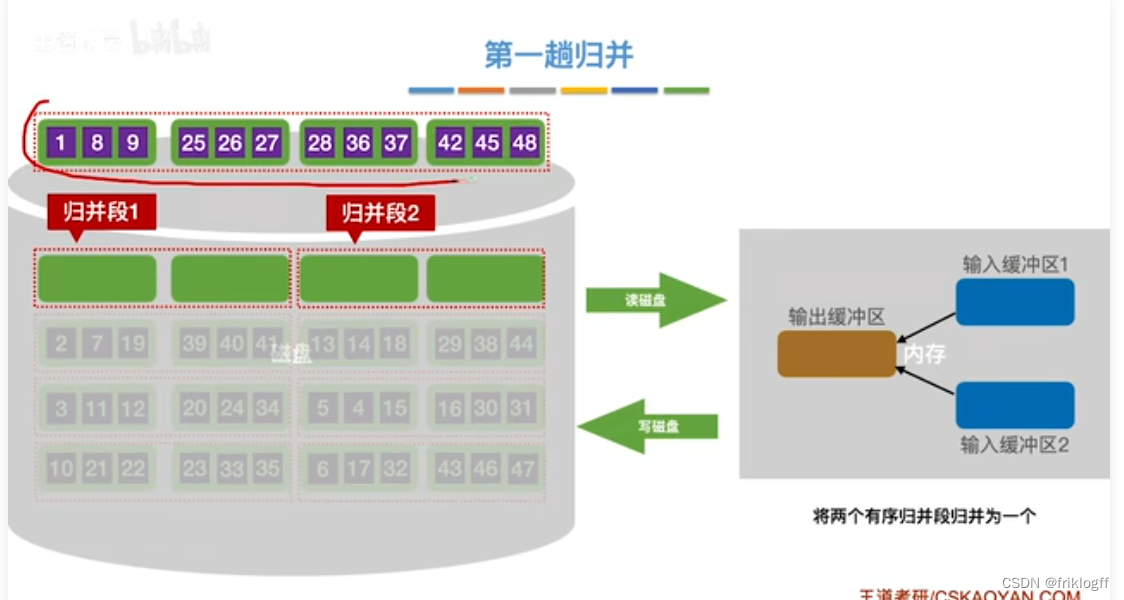
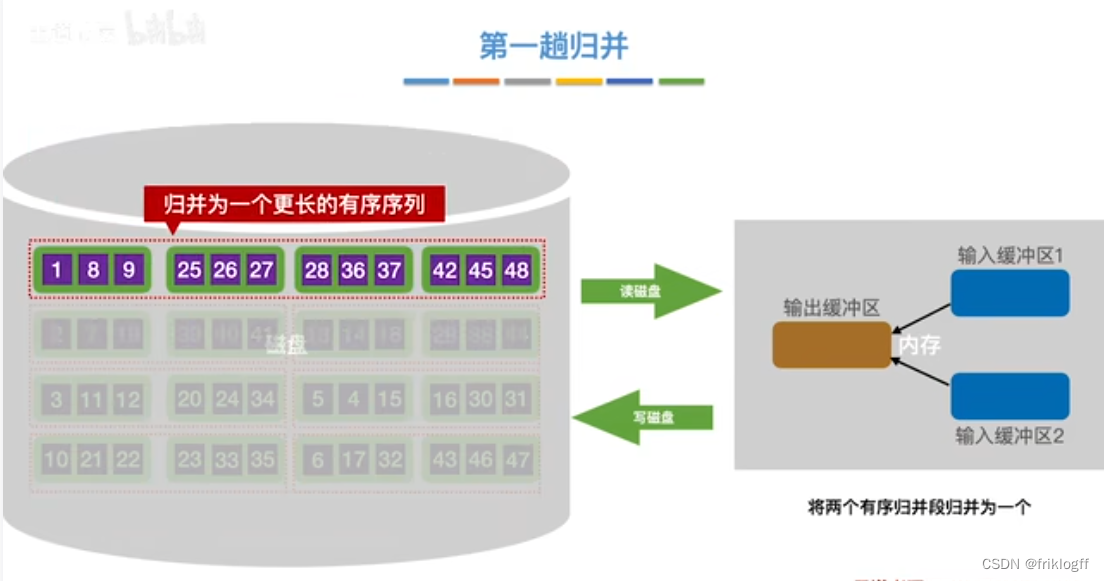
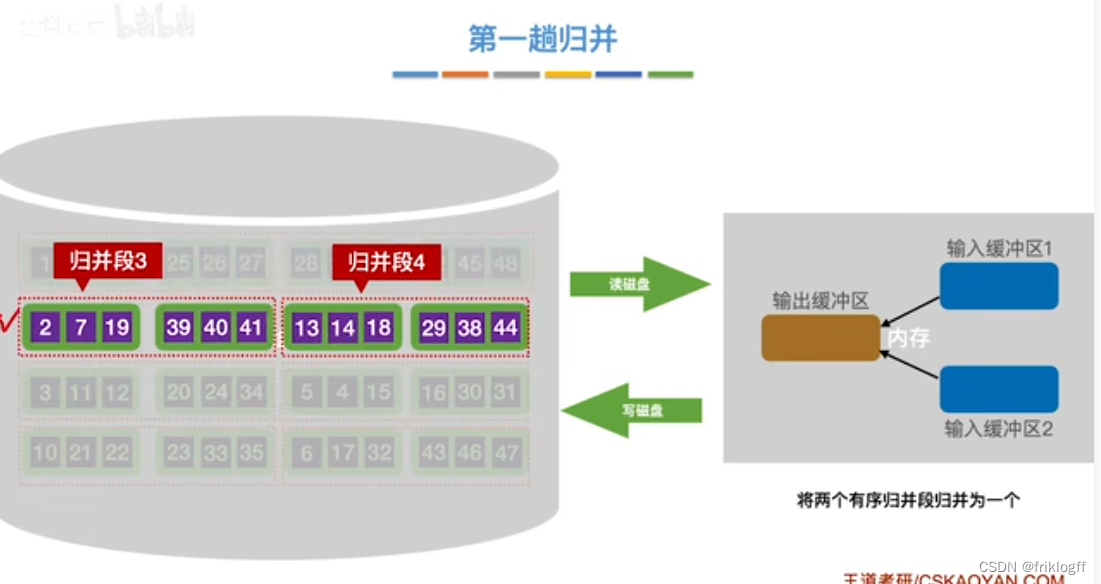
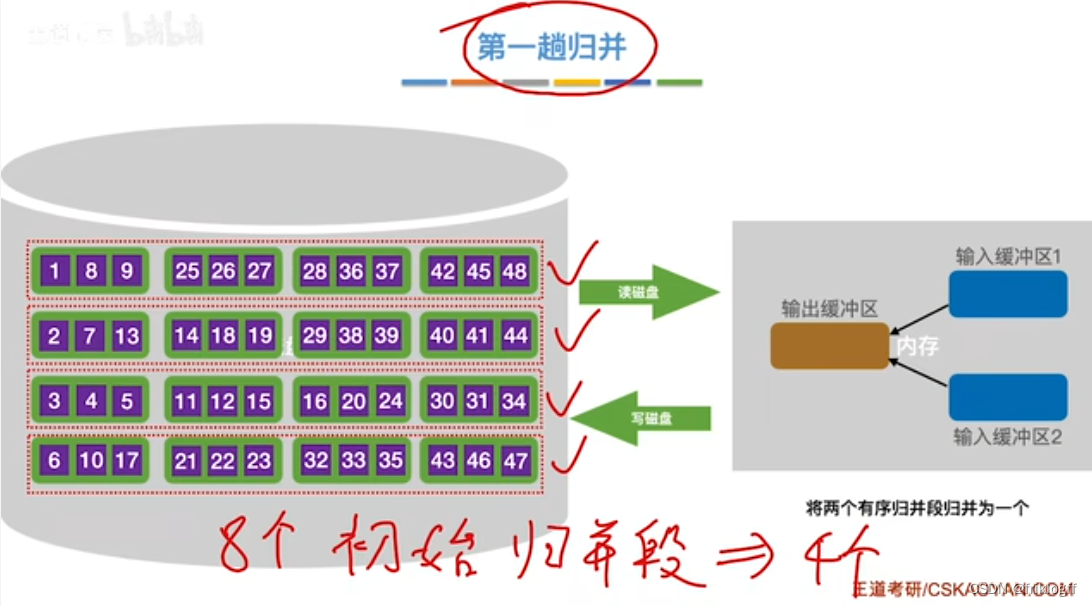
第二趟归并
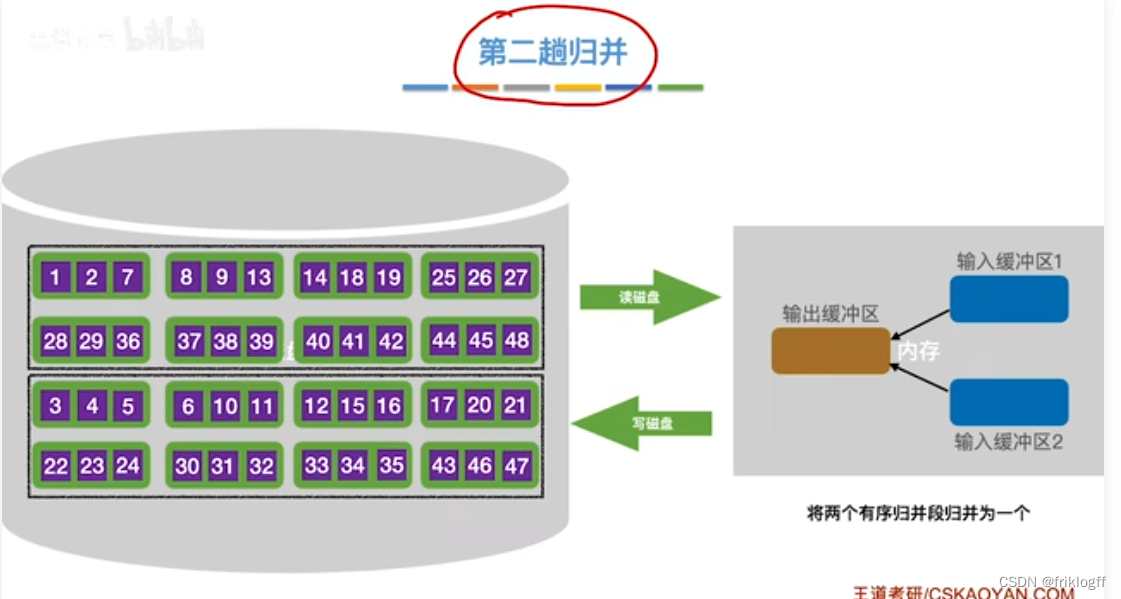
第三趟归并
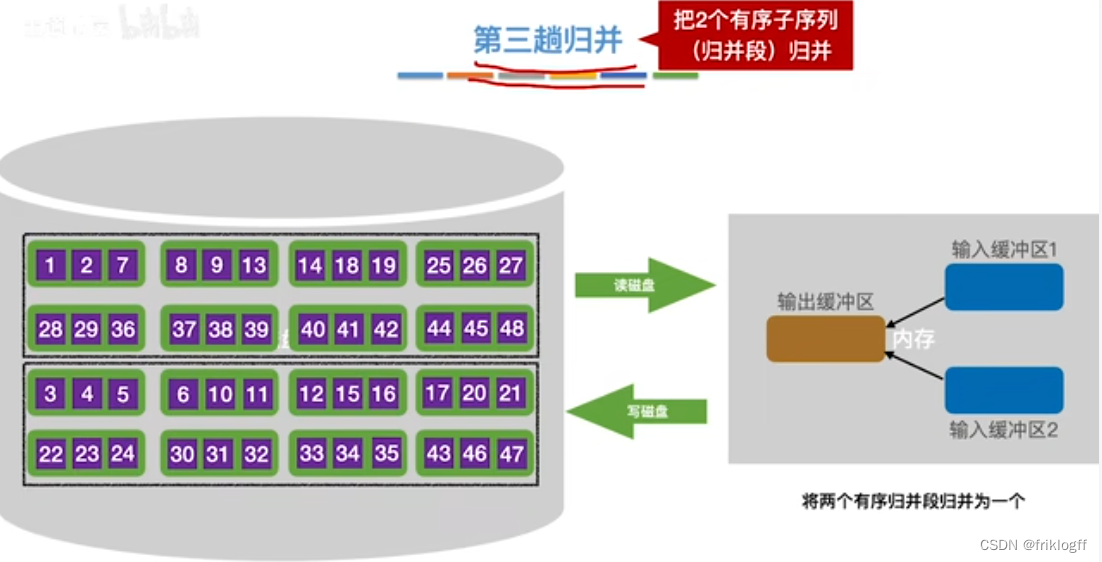
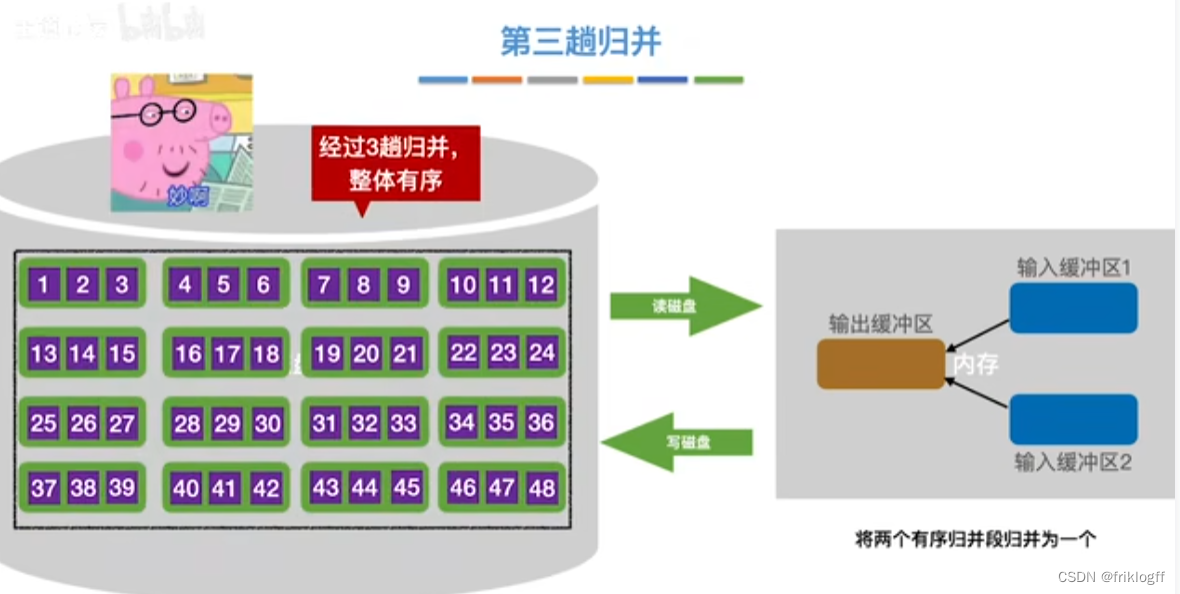
-
对大文件进行排序,因为文件中的记录很多、信息量庞大,无法将整个文件复制到内存进行排序
-
需要将待排序的记录存储在外存上,排序时再把数据一部分一部分地调入内存进行排序,在排序过程中需要多次进行内存和外存的交换
外部排序的方法
-
基本概念
-
文件通常是按块存储在磁盘上的,操作系统也按块读写
-
外部排序过程中的时间代价主要考虑访存次数(I/O次数)
-
-
步骤(采用归并排序)
-
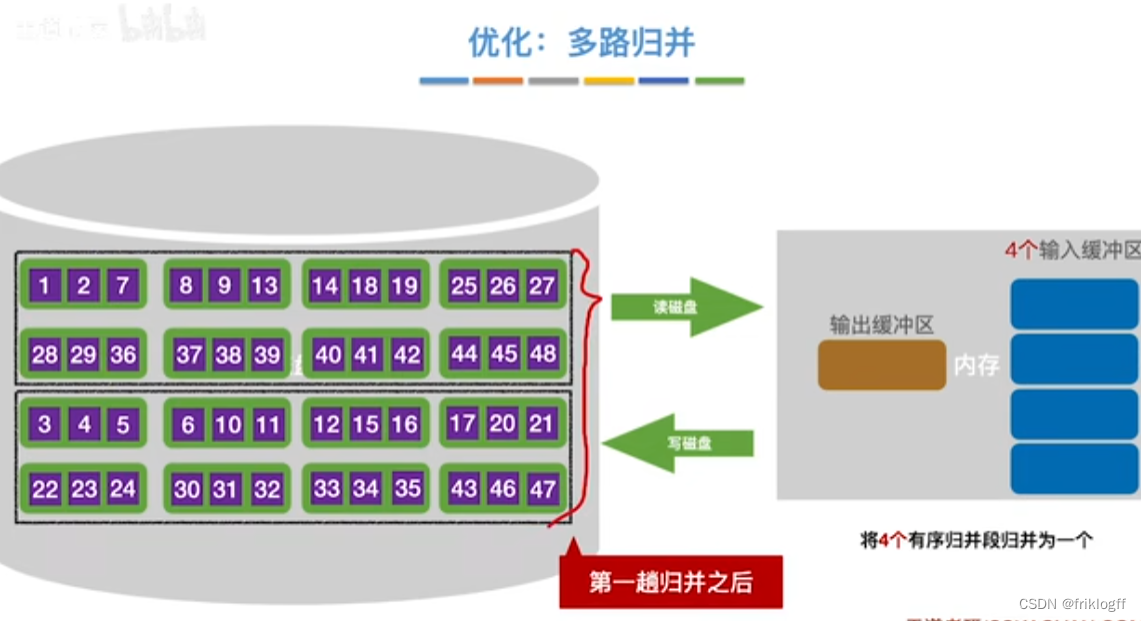
生成r个初始归并段(内部排序)
- 根据内存缓冲区大小,将外存文件分为r个子文件,依次读入内存并利用内部排序方法进行排序,并将内部有序的子文件重新写回外存
-
进行s躺k路归并
-
s = ⌈logk r⌉
-
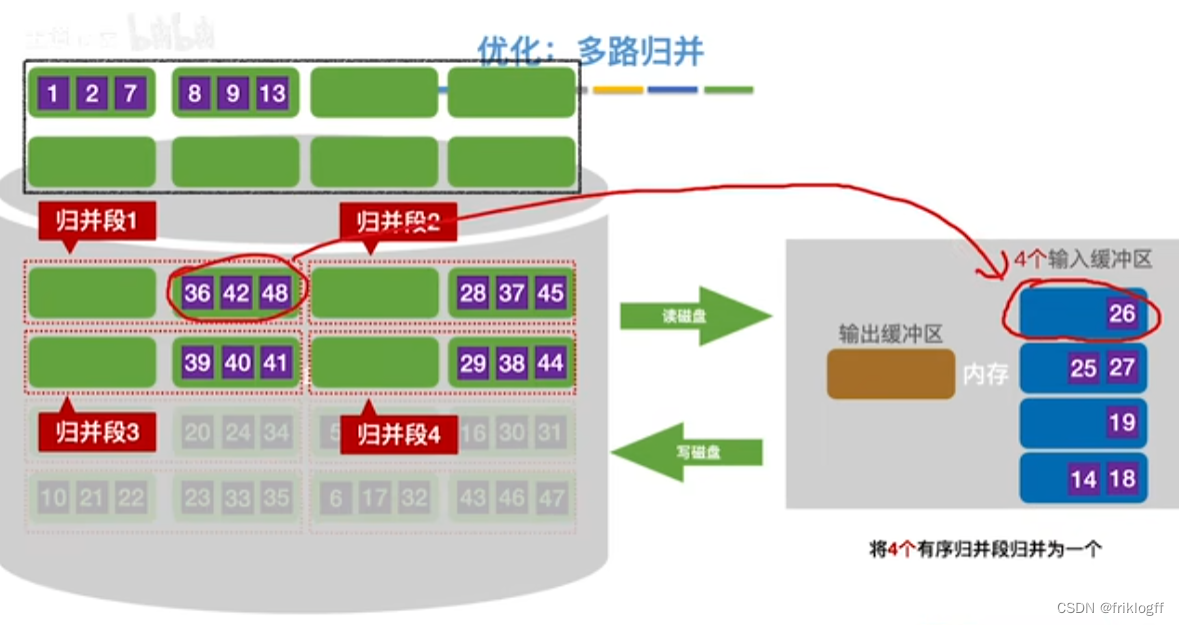
k路归并
-
将k个归并段的块读入k个输入缓冲区
-
用归并排序从k个归并段中选出几个最小记录暂存到输出缓冲区中
-
当输出缓冲区满时,写出外存
-
性质
-
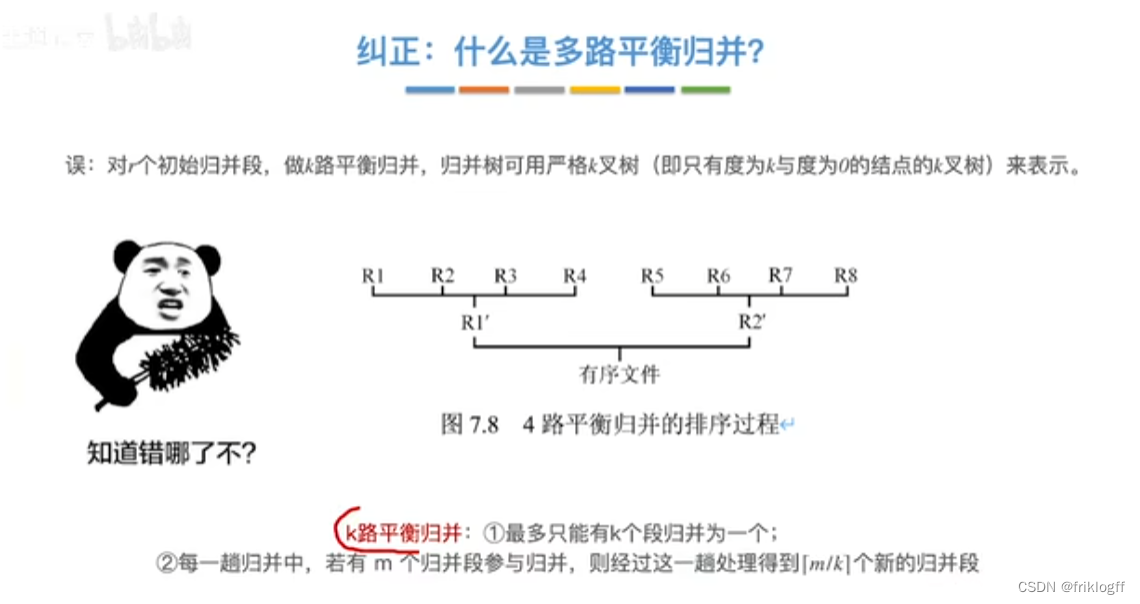
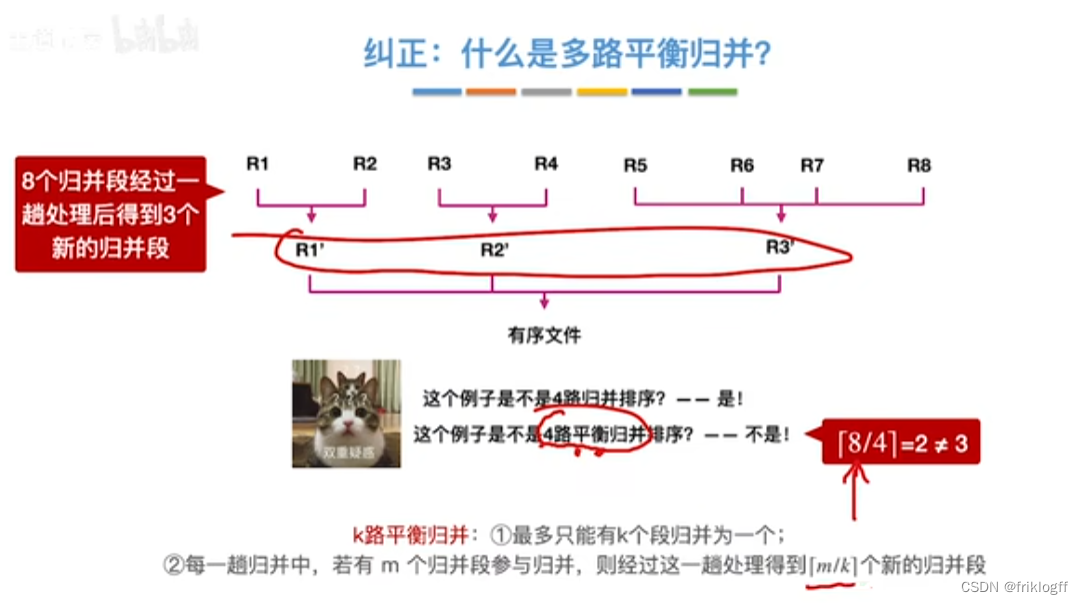
每趟归并中,最多只有k个段归并为一个
-
若总共有m个归并段参与,s趟归并后,得⌈m/k⌉新归并段
-
若要进行k路归并排序,内存需要1个输出缓冲区 + k个输入
-
-
-
-
-
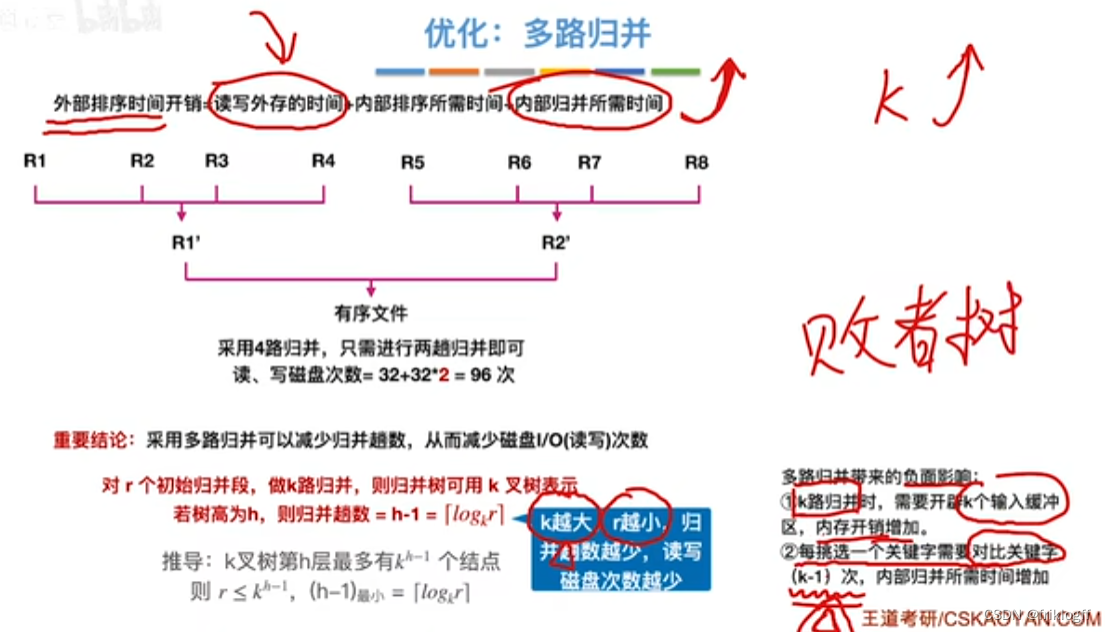
时间开销
- 读写外存时间+内部排序所需时间+内部归并所需时间

- 读写外存时间+内部排序所需时间+内部归并所需时间
优化(都减少归并趟数s,减少磁盘读写次数)
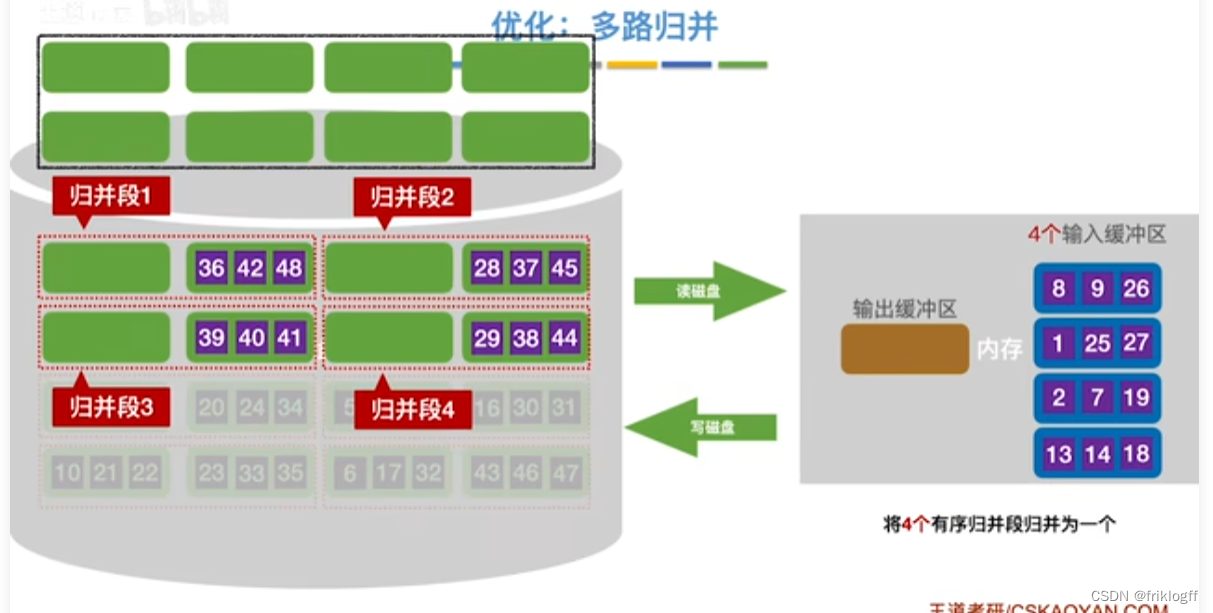
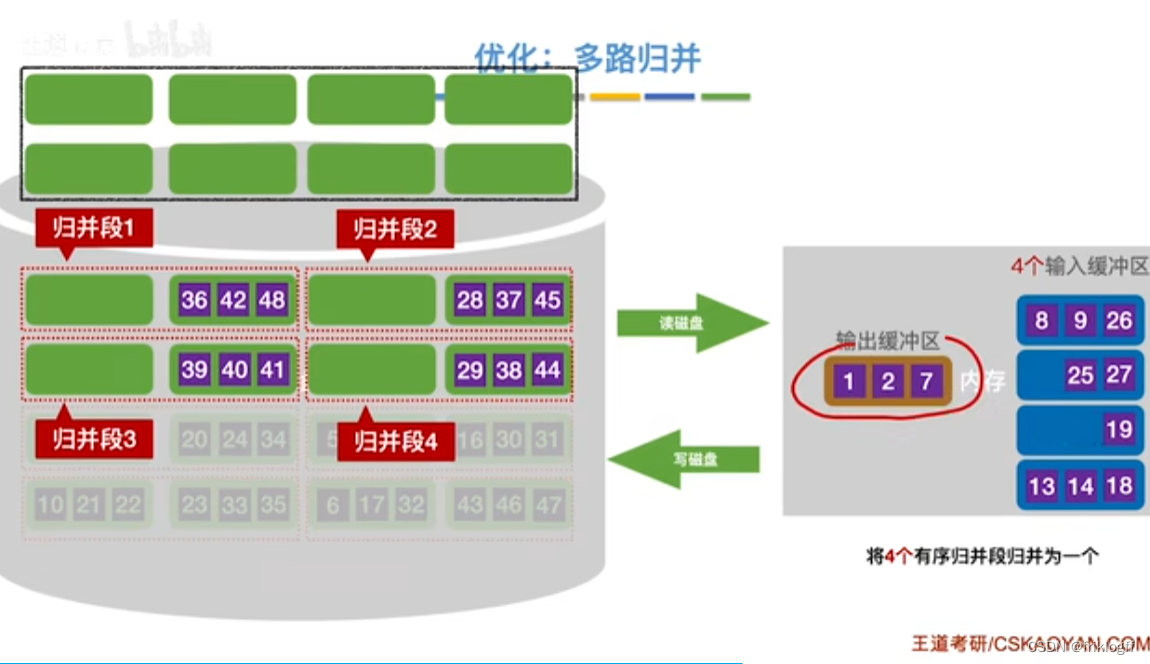

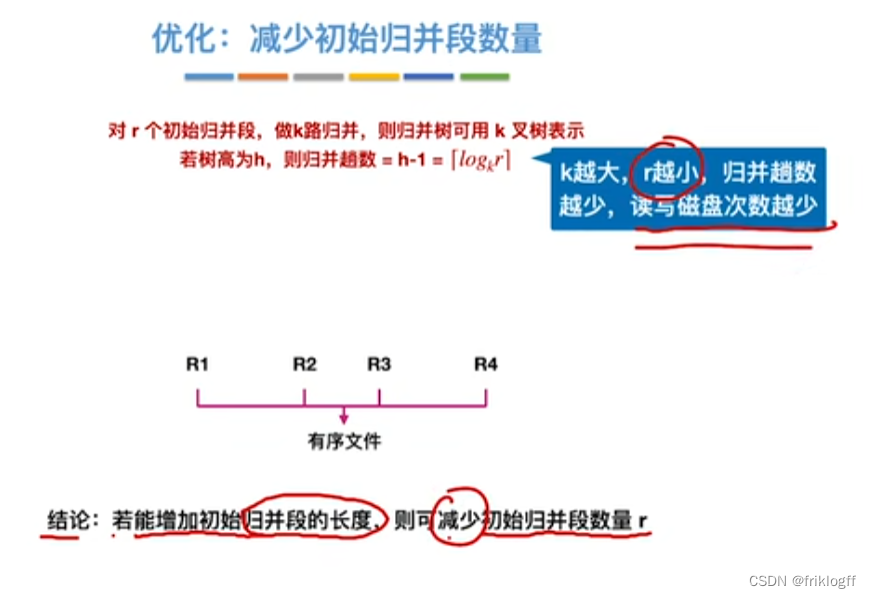
-
增大归并路数k,进行多路平衡归并
-
代价1:需要增加相应的输入缓冲区
-
代价2:每次从k个归并段中选一个最小元素需要(k-1)次关键字比较
-
-
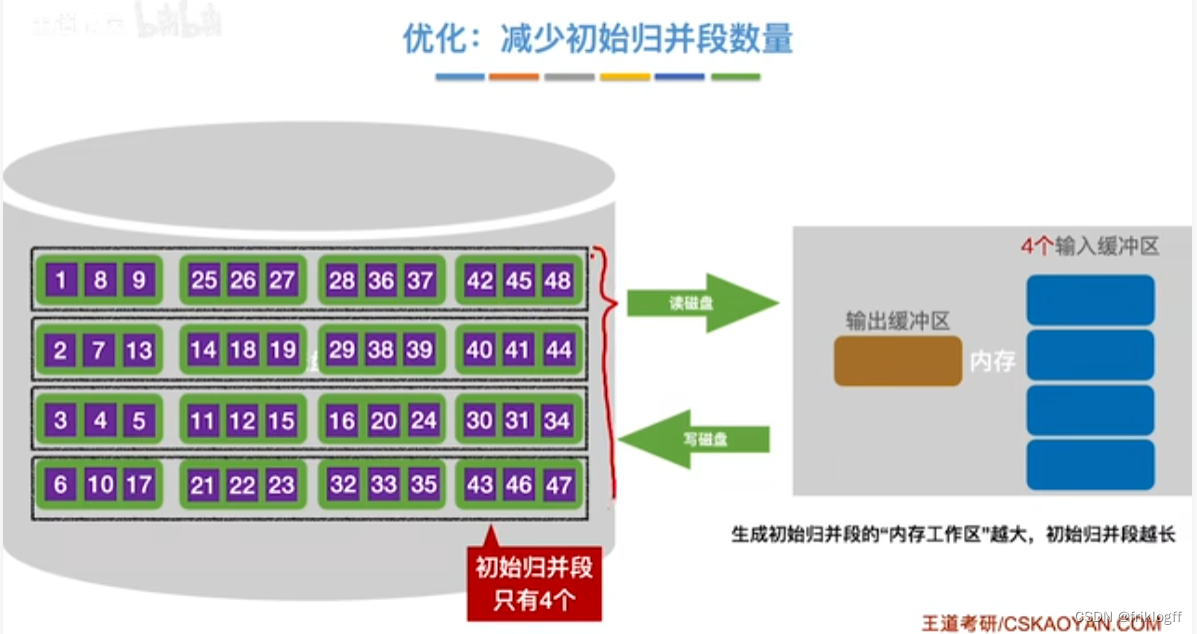
减少初始归并段个数r
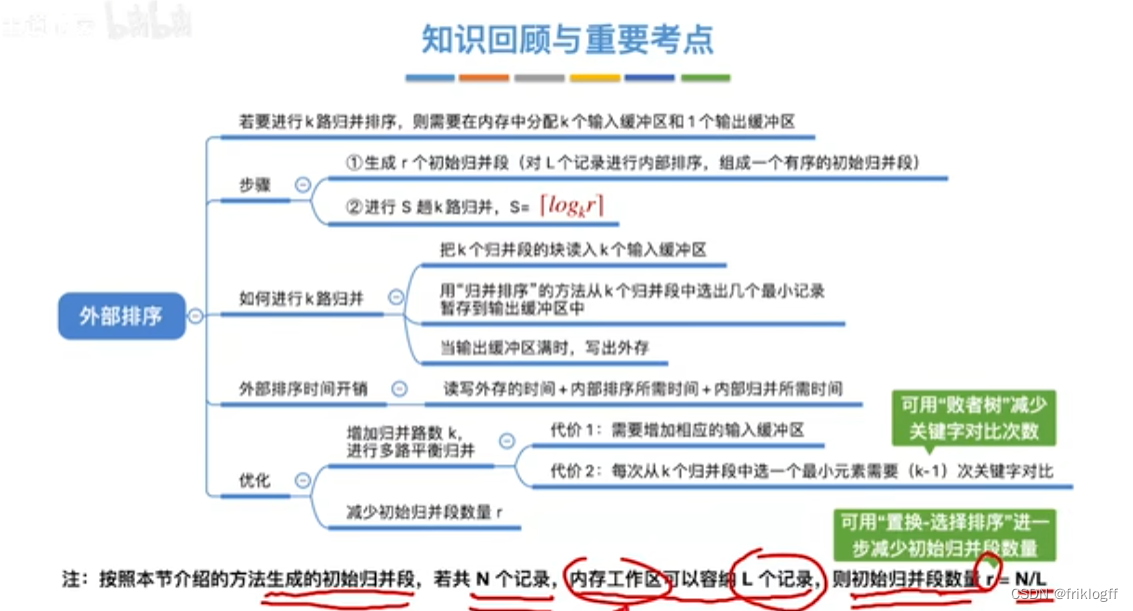
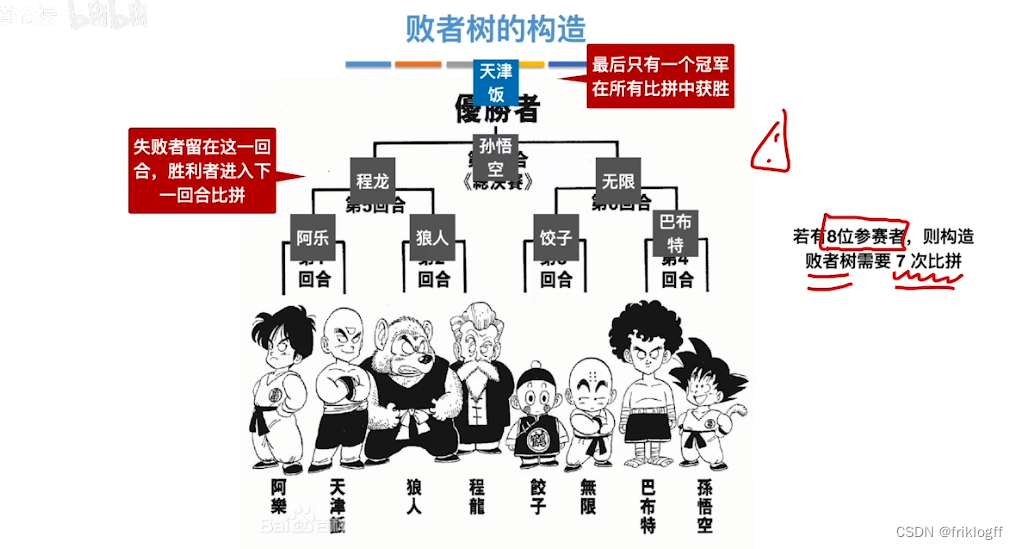
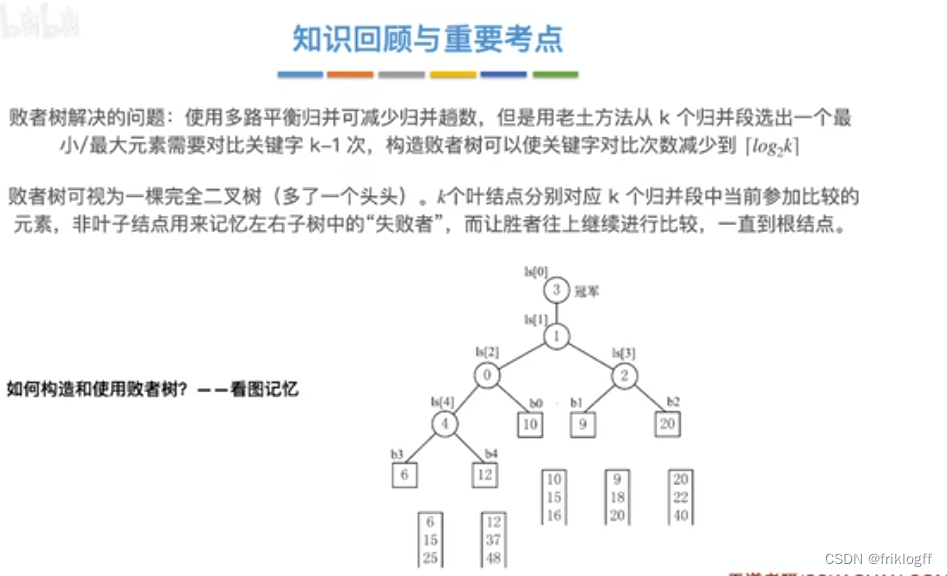
多路平衡归并与败者树
-

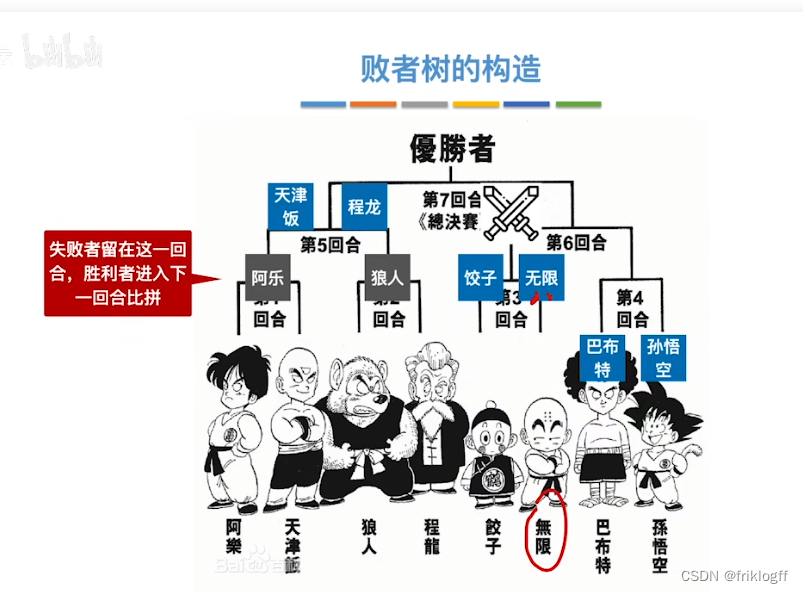
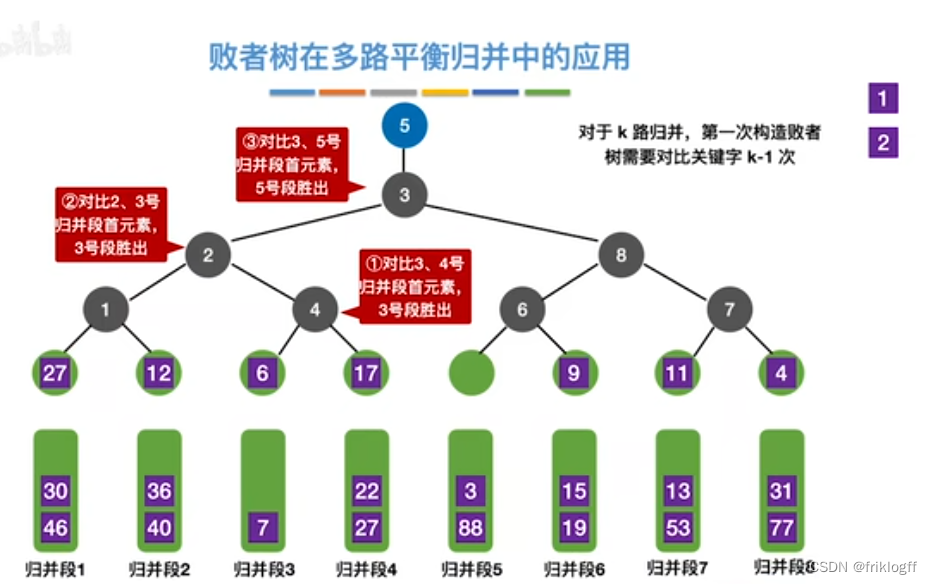
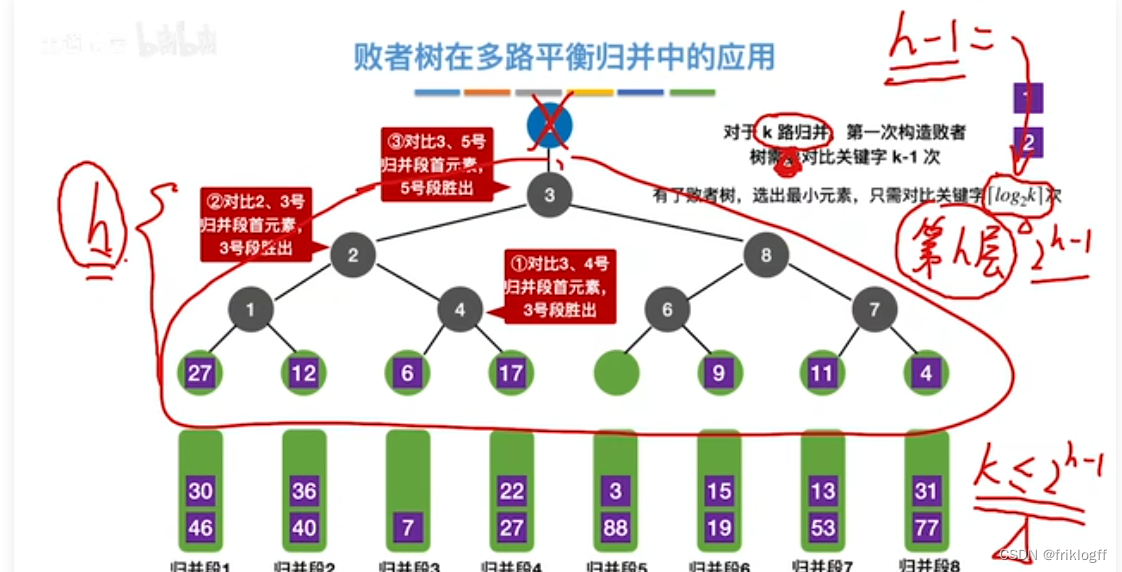
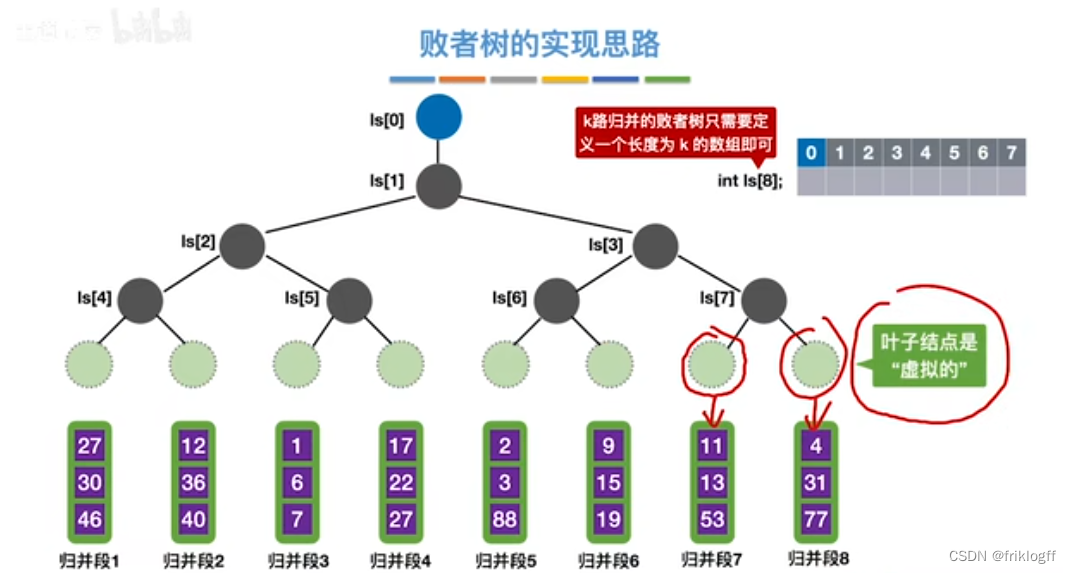
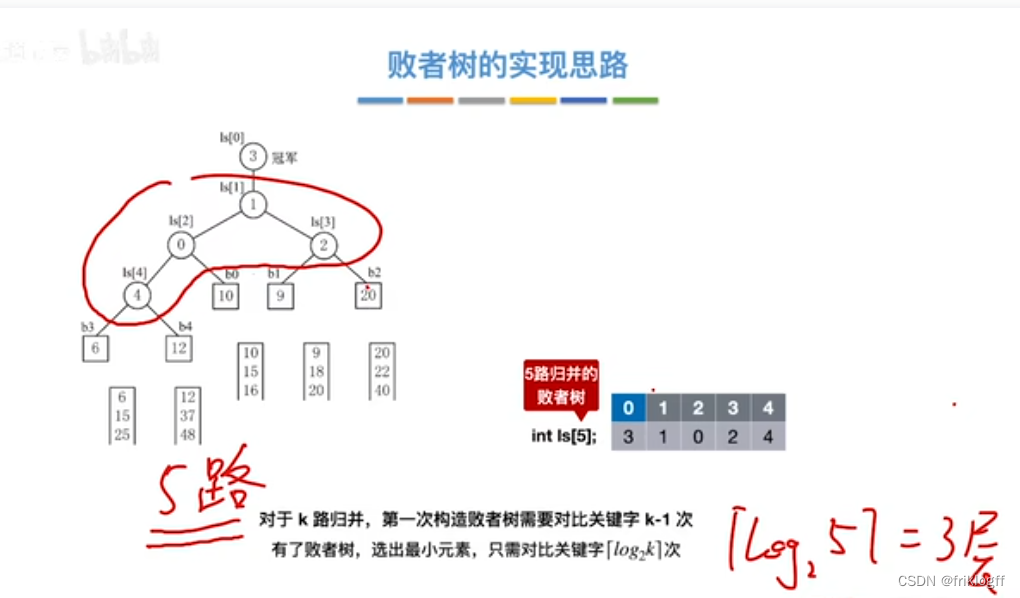
-
引入
- 为了减少优化1代价2,减少每次k个归并段找最小关键字的比较次数
-
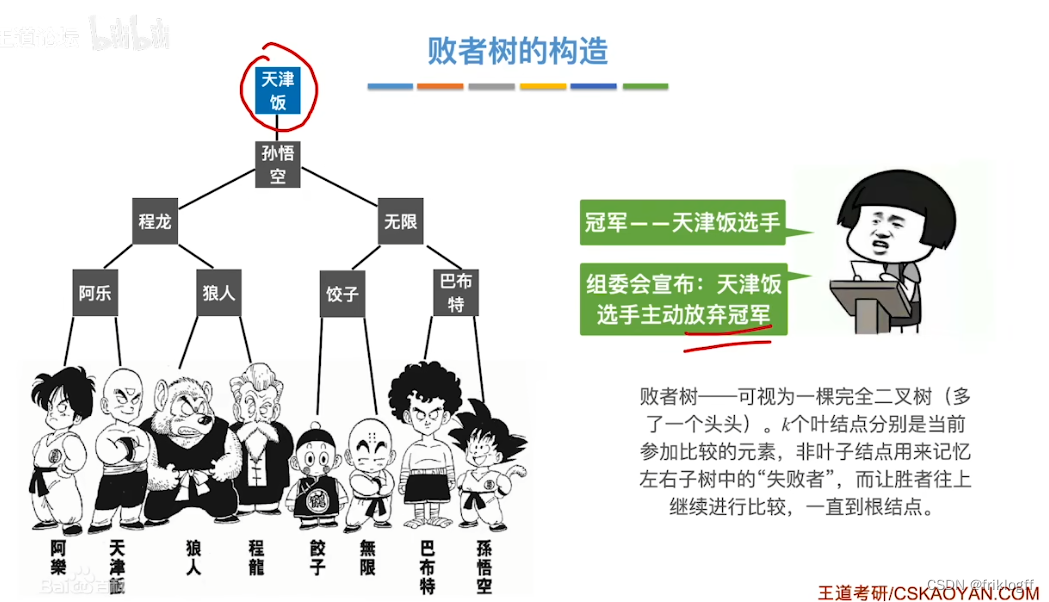
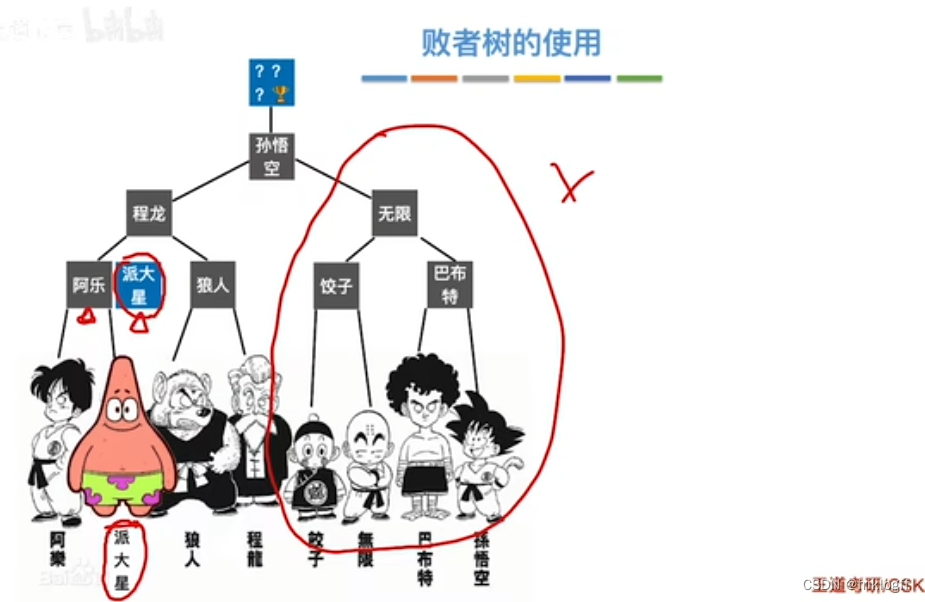
思想
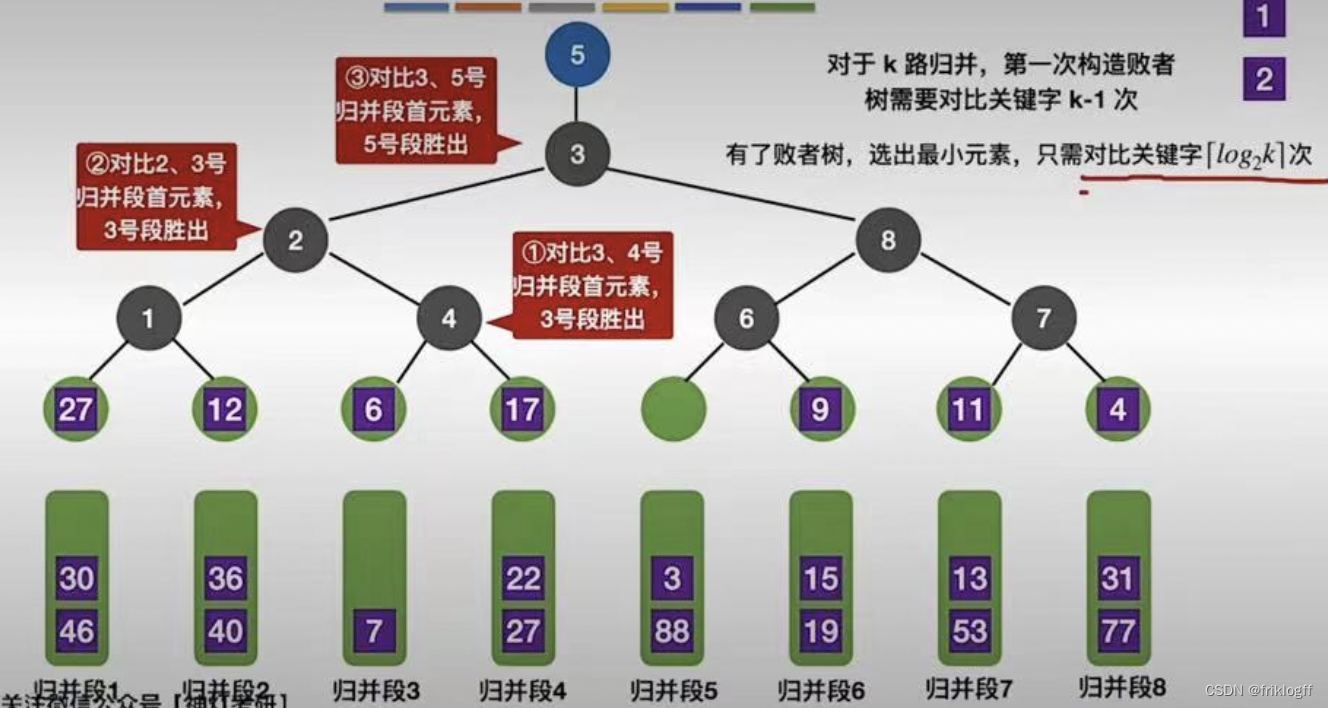
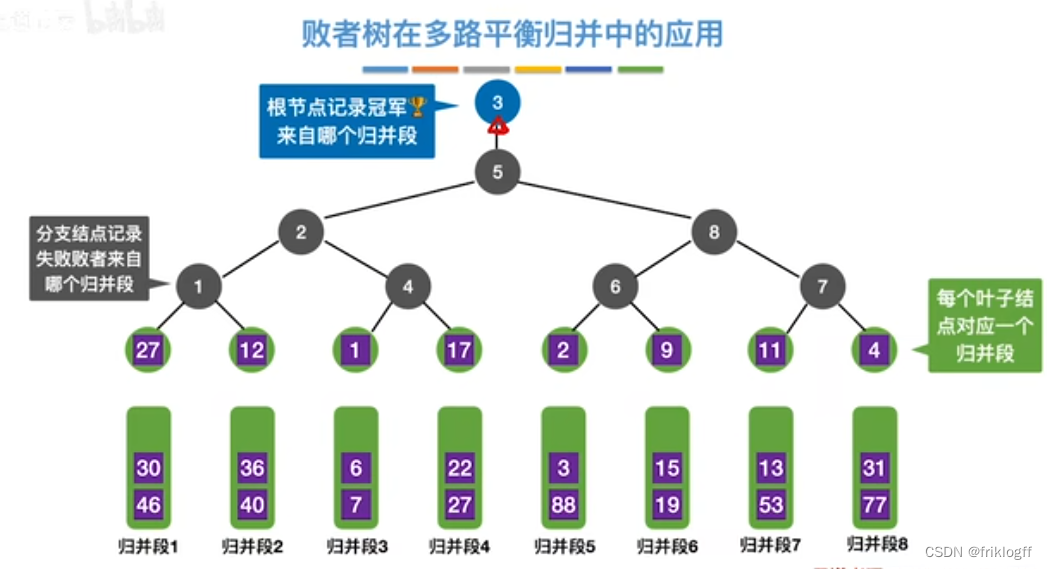
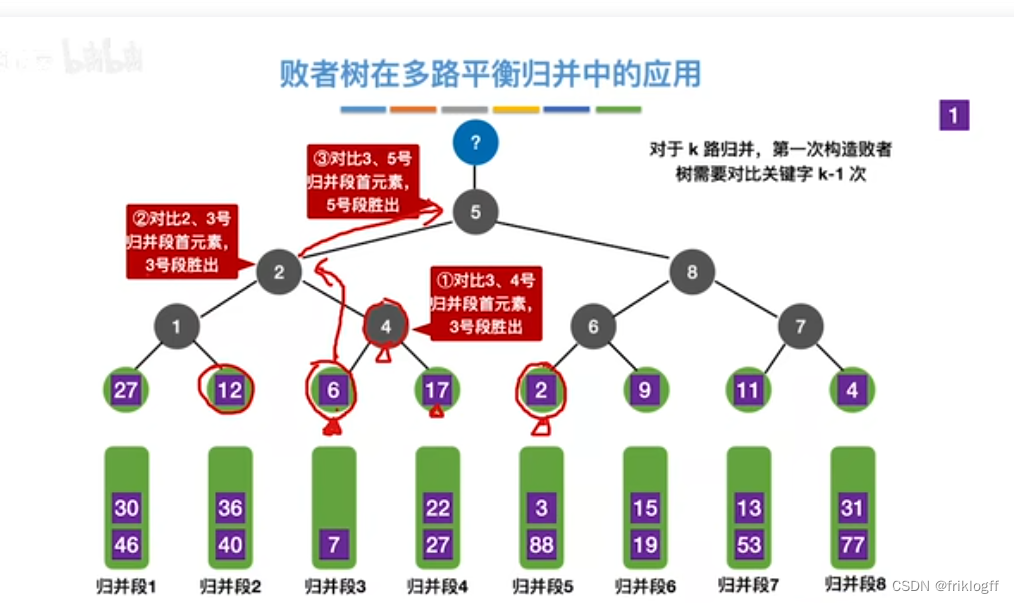
- k个叶结点分布存放k个归并段在归并过程中当前参加比较的记录,非叶结点用了记忆左右子树中“失败者”(记录段号),让胜者往上继续进行比较,直到根结点
-
性能
-
k路归并的败者树深度⌈log2 k⌉
-
总的比较次数由(n-1)(k-1)减少到(n-1)⌈log2 k⌉
-
-
注意:归并路数k过大时,虽然趟数减少,但读写外存次数仍会增加
-
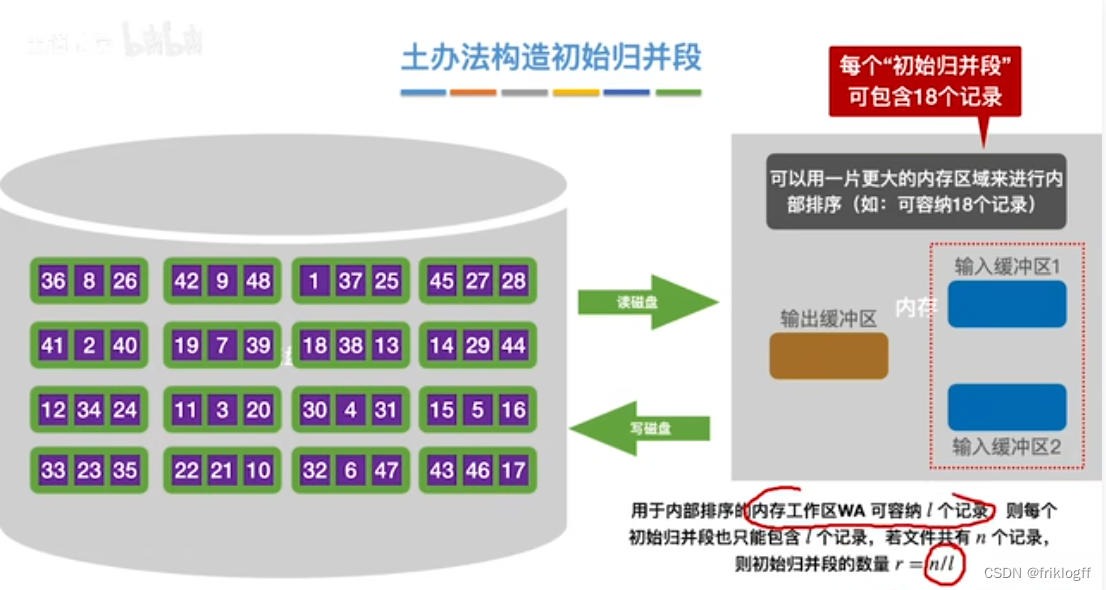
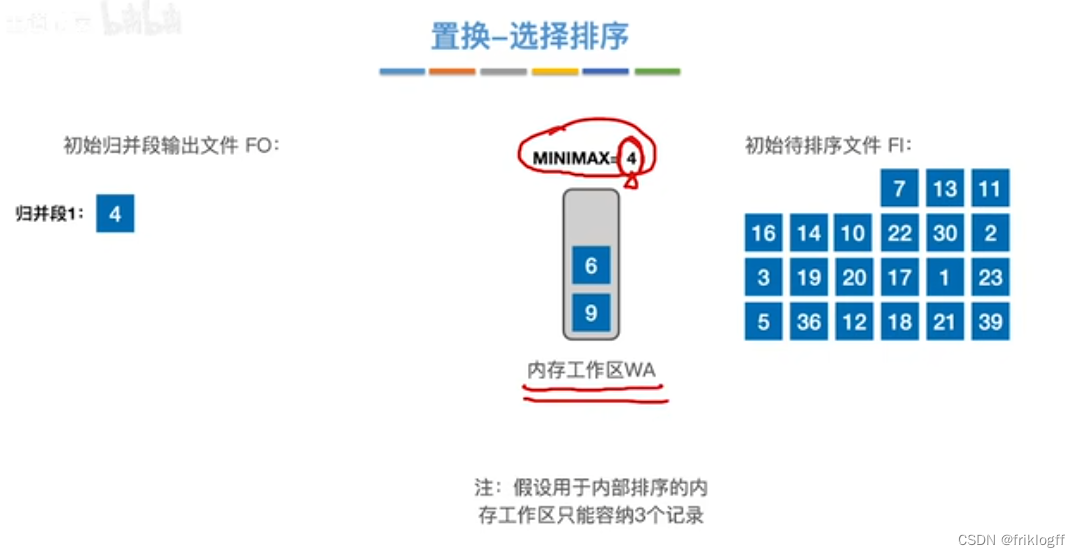
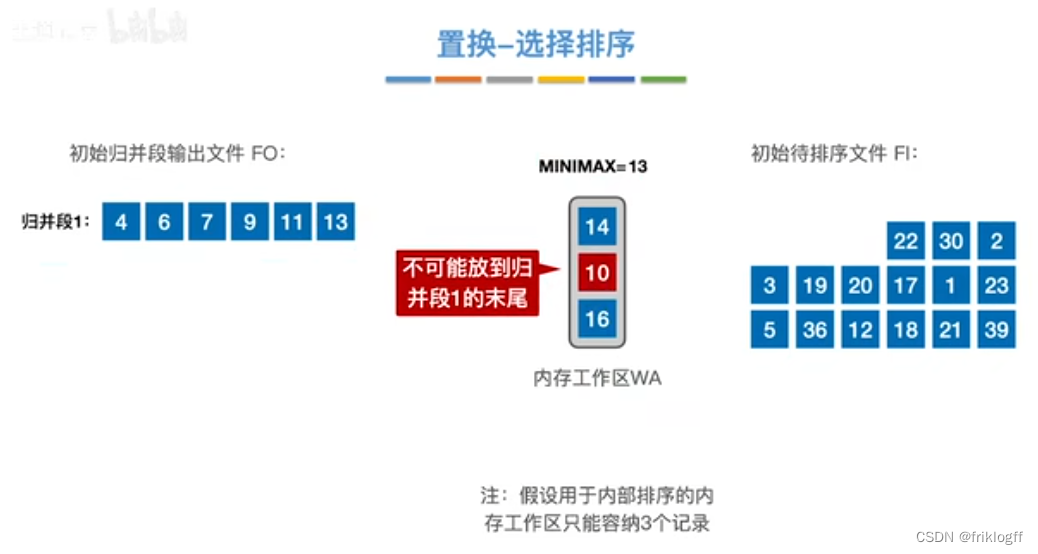
置换-选择排序(生成初始归并段)
-
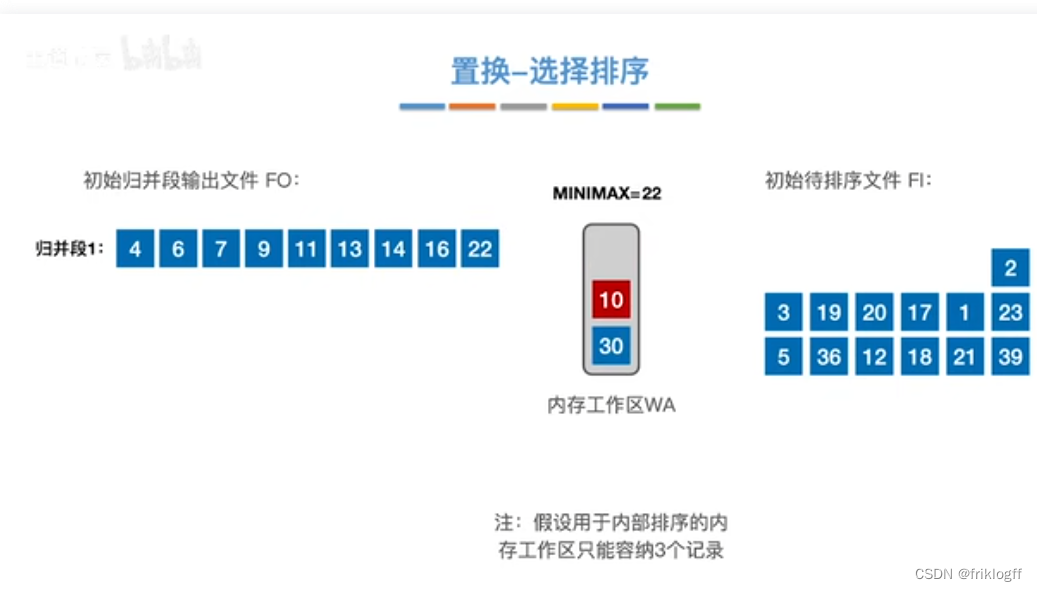
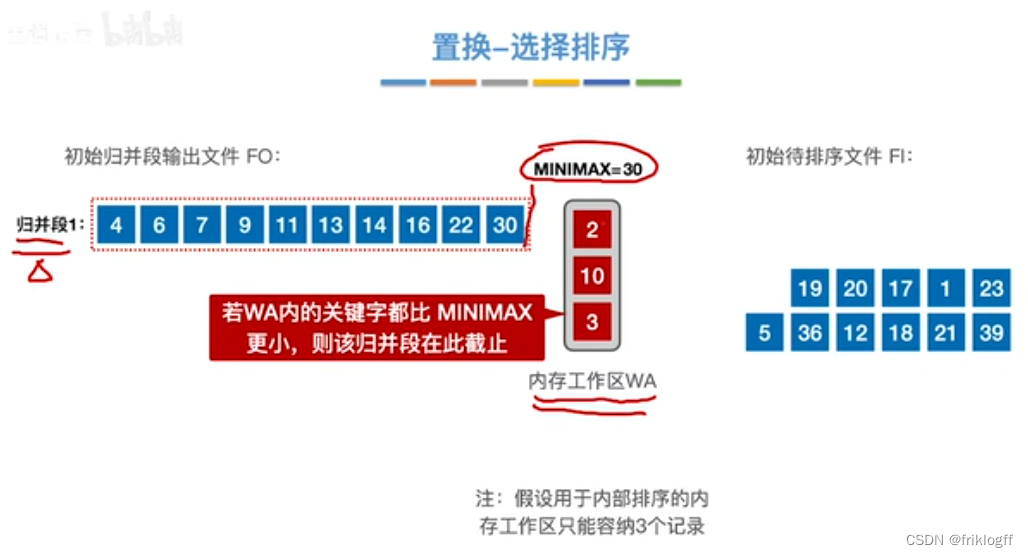
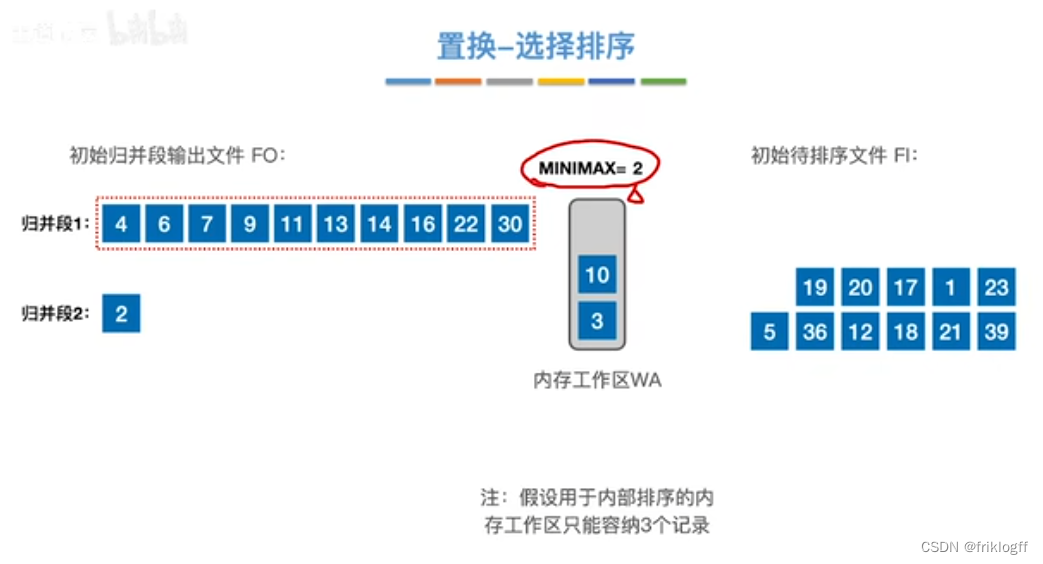

-
引入
- 即优化2:减少初始归并段数量r
-
实现:如图红字
-
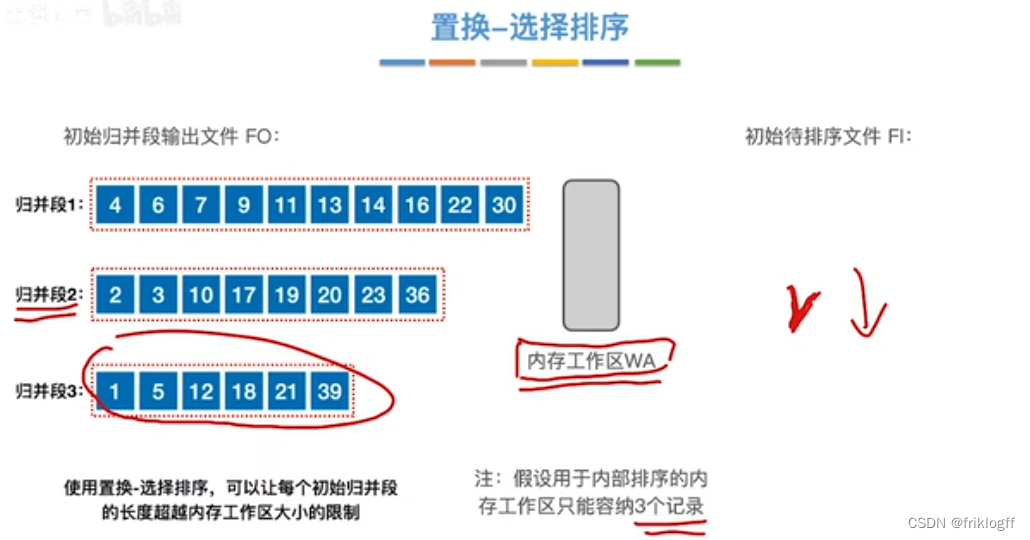

最佳归并树(k叉哈夫曼树)
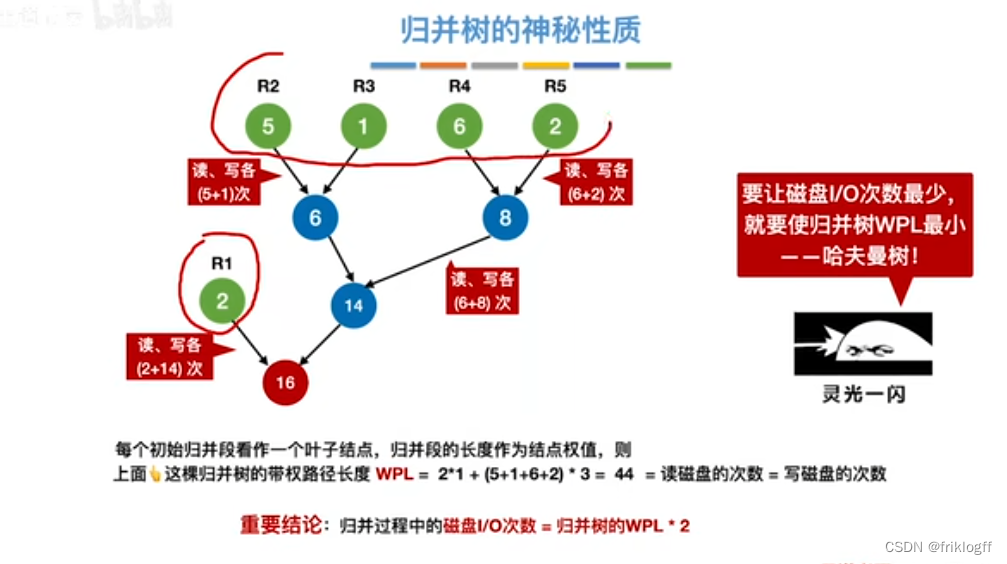
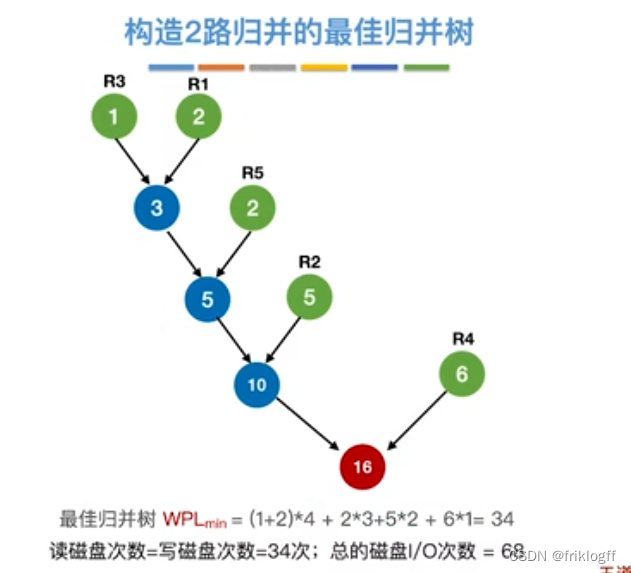
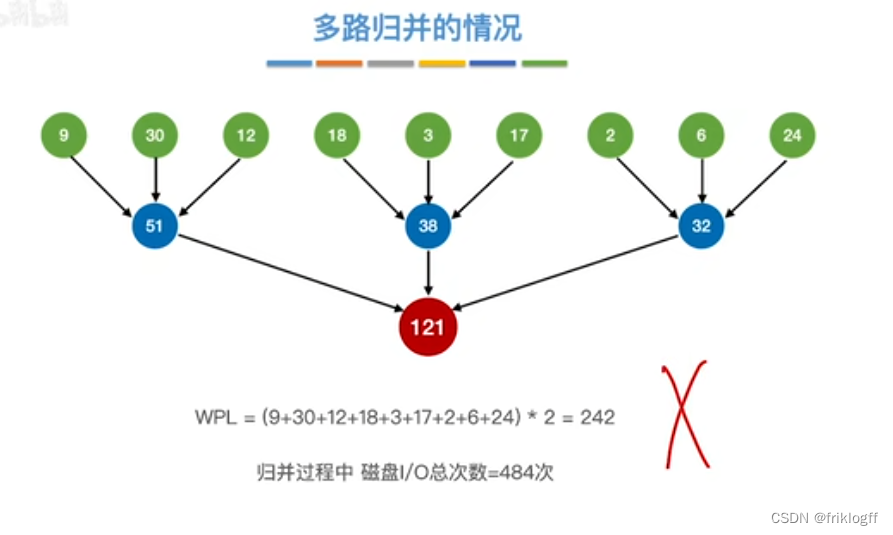
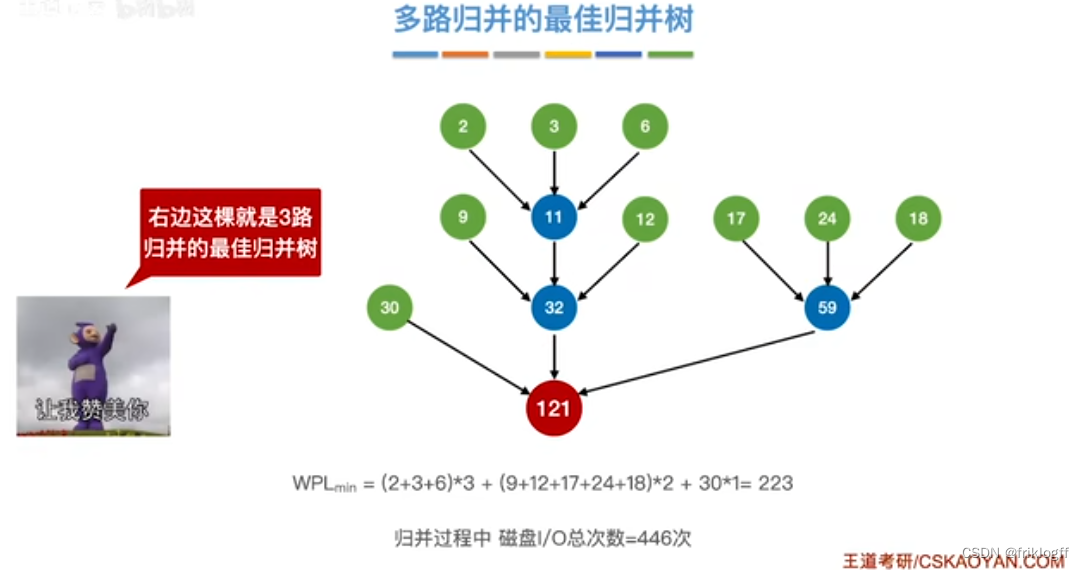
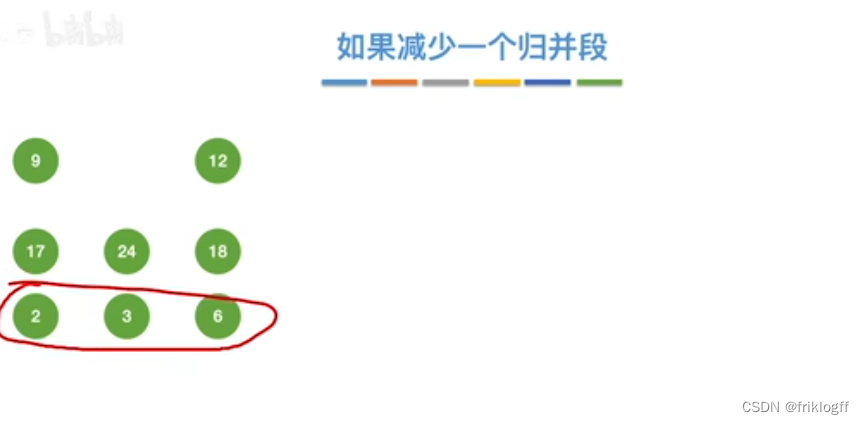
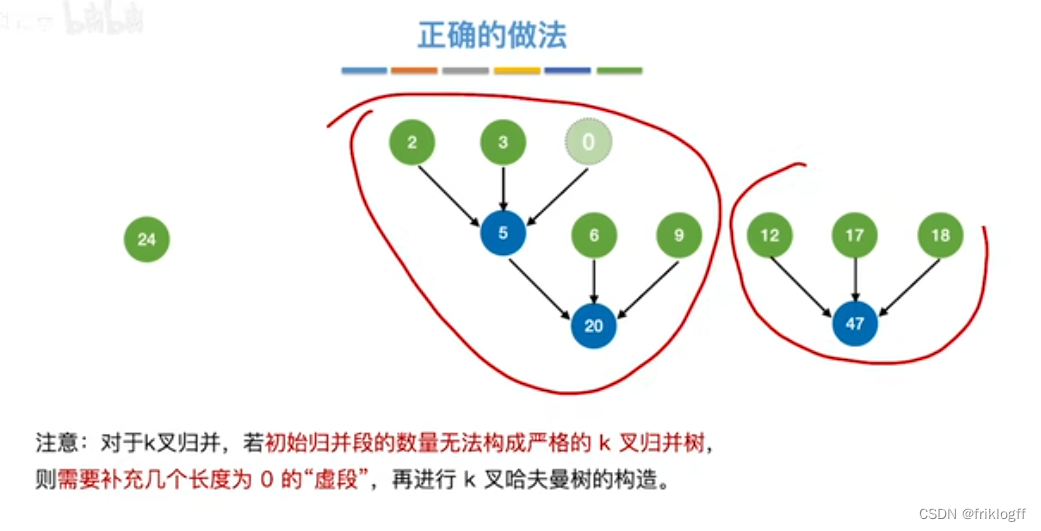
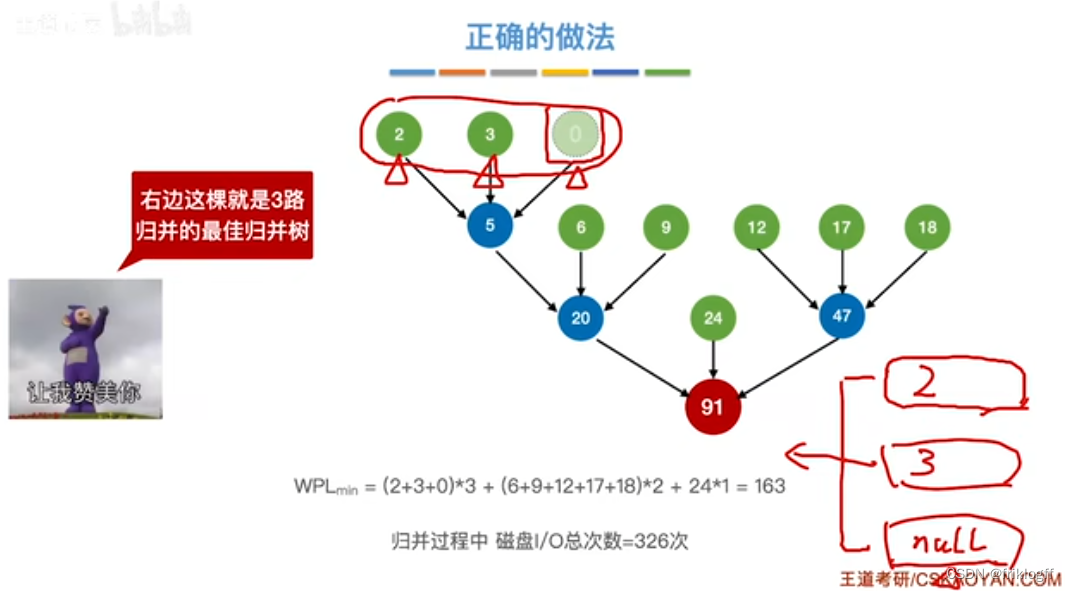

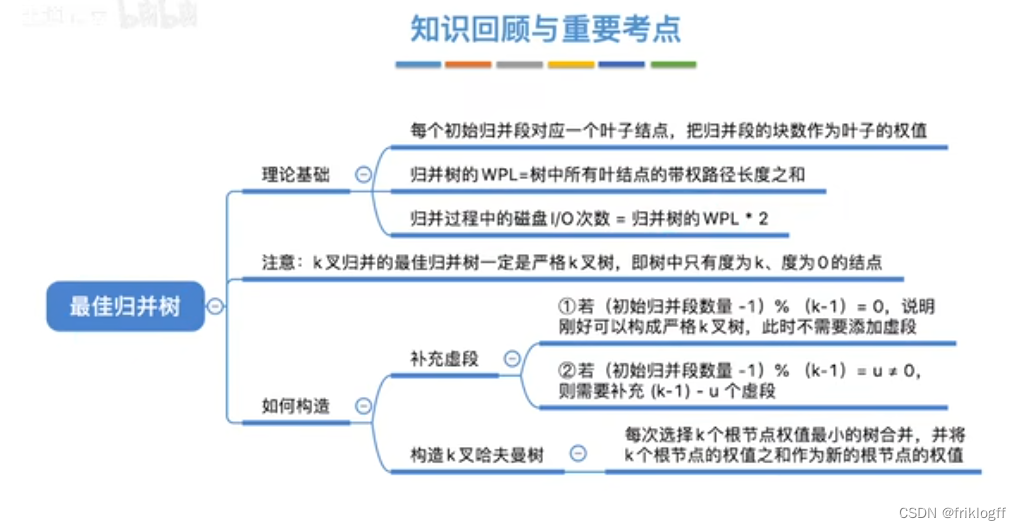
-
引入
- 为减少磁盘I/O次数(归并段读入读出,合并先后次序)
-
结构概述
-
叶结点表示初始归并段,权值表示该归并段的长度;非叶结点代表归并形成的新归并段
-
叶结点到根的路径长度表示其参加归并的趟数
-
归并树的带权路径长度WPL为归并过程中的总读记录数
-
归并过程中的磁盘I/O次数 = 归并树的WPL * 2
-
构造
-
补充虚段
-
若(初始归并段数量-1) % (k-1) = 0,说明刚好可以构成严格k叉树,此时无需添加虚段
-
若(初始归并段数量-1) % (k-1) = u != 0,则需要补充(k-1) - u个虚段
-
-
构造k叉哈夫曼树
- 每次选择k个根结点权值最小的树合并,并将k个根结点的权值之和作为新的根结点的权值
-
-
代码
快排
- 思路:基于分治思想
-
确定分界点(取左边界,去中间点,随机取)
-
调整区间,分<x与>x两部分分别是[l, j]、[j+1, r]
-
递归左右
-
void quick_sort(vector<int>&q, int l, int r){if (l >= r) return; //注意这里是>=int i = l - 1, j = r + 1, x = q[l + r >> 1];while (i < j){while (q[++i] < x); //注意这里无论结果如何i都会+1,故初始化时i=l-1,且才能跳出循环while (q[--j] > x);if (i < j) swap(q[i], q[j]);}quick_sort(q, l, j), quick_sort(q, j + 1, r);}
-
归并
- 思路:基于分治思想
-
确定分界点: 中间点 mid=l+r>>1
-
递归分界点左右
-
归并
-
void merge_sort(int q[], int l, int r){if (l >= r) return; //return边界int mid = l + r >> 1;merge_sort(q, l, mid); //排序左半merge_sort(q, mid + 1, r); //排序右半int k = 0, i = l, j = mid + 1; //将i,j分别指向两数组第一个元素while (i <= mid && j <= r) //若两数组都没结束,选小的进if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];else tmp[k ++ ] = q[j ++ ];while (i <= mid) tmp[k ++ ] = q[i ++ ]; //一数组结束,另外一数组剩下元素依次进while (j <= r) tmp[k ++ ] = q[j ++ ];for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];}
-
二分查找(可用于折半)
-
本质:可以划分为满足某种性质与不满足某种性质的两个区间,用二分法可以找到两区间边界的左右两个点。
-
int bsearch_1(int l, int r) //寻找右边界{while (l < r){int mid = l + r + 1 >> 1; //右边界需+1if (q[mid]>k) r = mid-1; //mid不满足<=,直接将右边界置mid左边else l = mid; //左边界一点点贴近右边界}return l;}int bsearch_2(int l, int r) //寻找左边界,同理{while (l < r){int mid = l + r >> 1;if (q[mid]<k) l = mid+1;else r = mid;}return l;}
-
相关文章:

【数据结构】考研真题攻克与重点知识点剖析 - 第 8 篇:排序
前言 本文基础知识部分来自于b站:分享笔记的好人儿的思维导图与王道考研课程,感谢大佬的开源精神,习题来自老师划的重点以及考研真题。此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析,本人技术…...

数字乡村可视化大数据-DIY拖拽式设计
DIY拖拽式大数据自由设计万村乐可视化大数据V1.0 随着万村乐数字乡村系统的广泛使用,我们也接收到了客户的真实反馈,最终在公司的决定下,我们推出了全新的可视化大数据平台V1.0版本,全新的可视化平台是一个通过拖拽配置生成可视化…...

数据集学习
1,CIFAR-10数据集 CIFAR-10数据集由10个类的60000个32x32彩色图像组成,每个类有6000个图像。有50000个训练图像和10000个测试图像。 数据集分为五个训练批次和一个测试批次,每个批次有10000个图像。测试批次包含来自每个类别的恰好1000个随机…...
【解决】npm run dev Syntax Error: TypeError: eslint.CLIEngine is not a constructor
问题: 由于代码语法不符合eslint而照成此错误,可以参照eslint规则修改语法,或者将eslint停掉 以下为停掉eslint的方法。 You may use special comments to disable some warnings. Use // eslint-disable-next-line to ignore the ne…...

Android 如何通过屏幕大小来适配不同大小的图片
可以使用Android中的dp(密度无关像素)单位来设置不同屏幕密度下的图片大小。dp是Android中的一种尺寸单位,它与屏幕密度无关,只与字体大小有关。在开发过程中,可以使用dp来设置布局和控件的大小,以便在不同的屏幕密度下保持一致的…...

【面试题】细说mysql中的各种锁
前言 作为一名IT从业人员,无论你是开发,测试还是运维,在面试的过程中,我们经常会被数据库,数据库中最经常被问到就是MySql。当面试官问MySql的时候经常会问道一个问题,”MySQL中有哪些锁?“当我…...
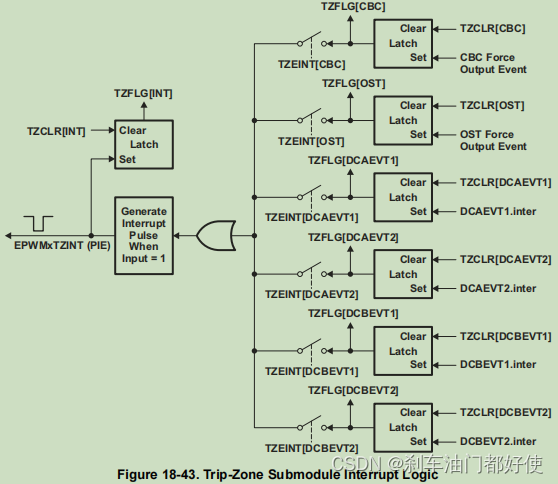
TMS320F280049 EPWM模块--TZ子模块(6)
下图是TZ子模块在epwm中的位置,可以看到TZ子模块接收内外部多种信号,经过处理后生成最终epwm波形,然后通过gpio向外发出。 TZ的动作有4个:拉高/拉低/高阻/不变。 TZ的内部框图见下图,可以看出: 1…...

数字乡村创新实践探索农业现代化路径:科技赋能农业产业升级、提升乡村治理效能与农民幸福感
随着信息技术的快速发展和数字化时代的到来,数字乡村建设正成为推动农业现代化、提升农业产业竞争力、优化乡村治理以及提高农民幸福感的重要途径。本文将围绕数字乡村创新实践,探讨其在农业现代化路径中的积极作用,以及如何通过科技赋能实现…...

linux中rpm包与deb包的区别及使用
文章目录 1. rpm与deb的区别2. deb软件包的格式和使用2.1 deb软件包命令遵行如下约定2.2 dpkg命令2.3 apt-命令 3. Unix和Linux的区别Reference 1. rpm与deb的区别 有的系统只支持使用rpm包安装,有的只支持deb包安装,混乱安装会导致系统问题。 关于rpm和…...
Linux中安装seata
Linux中安装seata 一、准备1、环境2、下载3、上传到服务器4、解压 二、配置1、备份配置文件2、导入sql3、修改配置前4、修改配置后5、在nacos中配置 三、使用1、启动2、关闭 一、准备 1、环境 因为要在 nacos 中配置,要求安装并启动 nacos 。可以参考这篇博客。 …...
预印本仓库ArXiv——防止论文录用前被别人剽窃
文章目录 一、什么是预印本二、什么是ArXiv2.1 ArXiv的领域2.2 如何使用 一、什么是预印本 预印本(Preprint)是指科研工作者的研究成果还未在正式出版物上发表,而出于和同行交流目的自愿先在学术会议上或通过互联网发布的科研论文、科技报告…...

LNMP 架构
1. 环境准备 环境准备 lnmp 需要 安装 nginx mysql php 软件 1.1 关闭防火墙 systemctl disable --now firewalld setenforce 0 1.2 安装依赖包 yum -y install pcre-devel zlib-devel gcc gcc-c make 1.3 创建运行用户、组 (Nginx 服务程序默认以 nobody 身份…...

谈谈Python中的单元测试和集成测试
谈谈Python中的单元测试和集成测试 Python中的单元测试和集成测试是软件开发过程中的重要环节,它们确保了代码的质量和稳定性。单元测试主要关注代码的最小可测试单元——通常是函数或类的方法,而集成测试则关注这些单元之间的协作和交互。下面…...

【2024】Prometheus通过node_exporter都监控了什么
我们通过prometheus进行监控,通过node_exporter进行Linux系统的监控。 那么我们通过node_exporter都监控了什么? 目录 常用指标CPU相关内存相关磁盘相关网络相关其他指标常用监控告警案例:cpu案例:内存案例:磁盘案例:网络案例:常用指标 Prometheus通过node_exporter可以…...
Centos7配置秘钥实现集群免密登录
设备:MacBook Pro、多台Centos7.4服务器(已开启sshd服务) 大体流程:本机生成秘钥,将秘钥上传至服务器即可实现免密登录 1、本地电脑生成秘钥: ssh-keygen -t rsa -C "邮箱地址 例:*****.163.com"一路回车…...
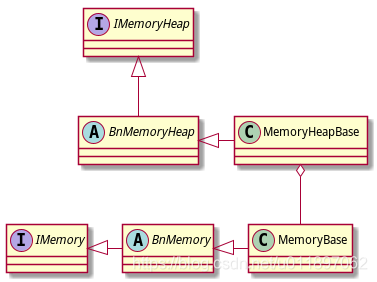
Android匿名共享内存(Ashmem)
在Android中我们熟知的IPC方式有Socket、文件、ContentProvider、Binder、共享内存。其中共享内存的效率最高,可以做到0拷贝,在跨进程进行大数据传输,日志收集等场景下非常有用。共享内存是Linux自带的一种IPC机制,Android直接使用…...

MySOL之旅--------MySQL数据库基础( 3 )
本篇碎碎念:要相信啊,胜利就在前方,要是因为一点小事就停滞不前,可能你也不适合获取胜利,成功的路上会伴有泥石,但是走到最后,你会发现身上的泥泞皆是荣耀的勋章! 今日份励志文案: 凡是发生皆有利于我 目录 查询(select) 1.全列查询 2.指定列查询 3.查询字段为表达式 编…...
)
阿药陪你学Java(第零讲)
第零讲:基本数据类型 Java包括两种数据类型,分别是内置数据类型(基本数据类型)和引用数据类型。 内置数据类型 Java提供了8中内置类型,其中包括4种数字整型、2种数字浮点型、1中字符型、1中布尔型。下面进行详细介绍…...
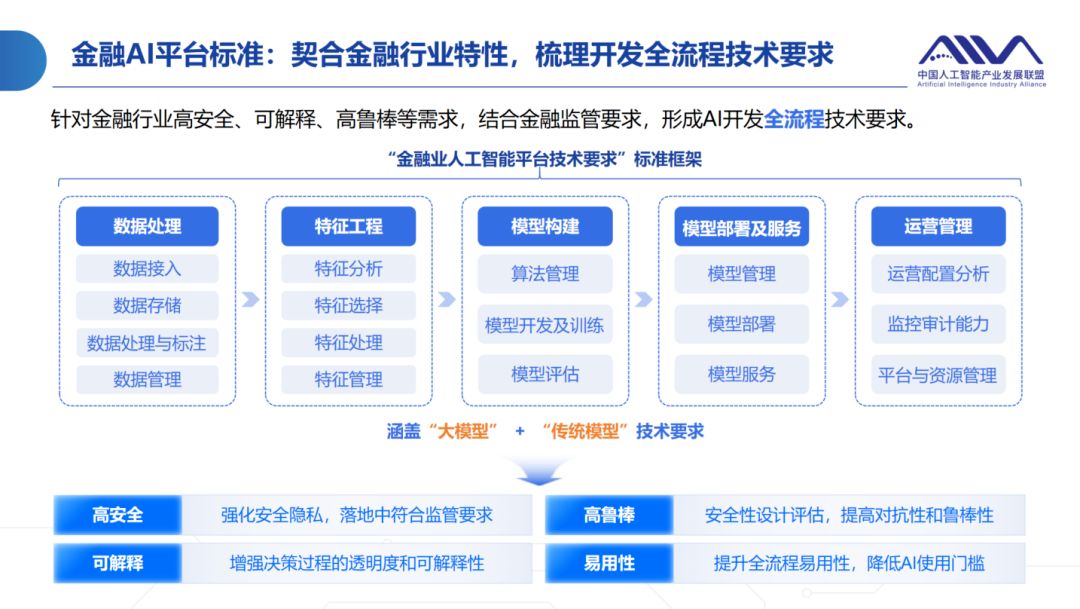
华院计算参编《金融业人工智能平台技术要求》标准
随着人工智能技术的迅猛发展,金融机构正在从业务场景化向企业智能化演进,金融业对智能化的需求愈加迫切。为引导产业有序发展、规范行业自律、加快金融行业智能化转型,中国信通院依托中国人工智能产业发展联盟(AIIA)及…...

vue3-element-admin二次开发遇到的问题总结,持续更新中
vue3-element-admin 是基于 Vue3 Vite5 TypeScript5 Element-Plus Pinia 等主流技术栈构建的免费开源的后台管理前端模板(配套后端源码)。 一、定制Element-Plus主题 1.创建 variables.scss 变量文件 /*variables.scss*/ /*覆盖element-plus变量*/…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...