初识二叉树和二叉树的基本操作
目录
一、树
1.什么是树
2. 与树相关的概念
二、二叉树
1.什么是二叉树
2.二叉树特点
3.满二叉树与完全二叉树
4.二叉树性质
相关题目:
5.二叉树的存储
6.二叉树的遍历和基本操作
二叉树的遍历
二叉树的基本操作
一、树
1.什么是树
- 子树是不相交的;
- 除了根结点外,每个结点有且仅有一个父结点
- 一棵N个结点的树有N-1条边。
树: 非树:
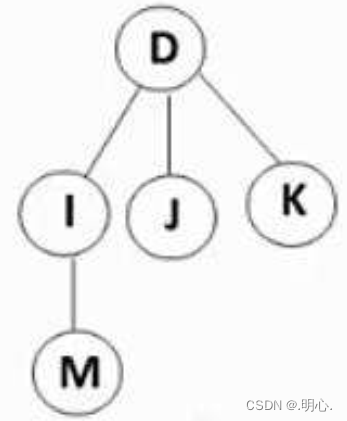
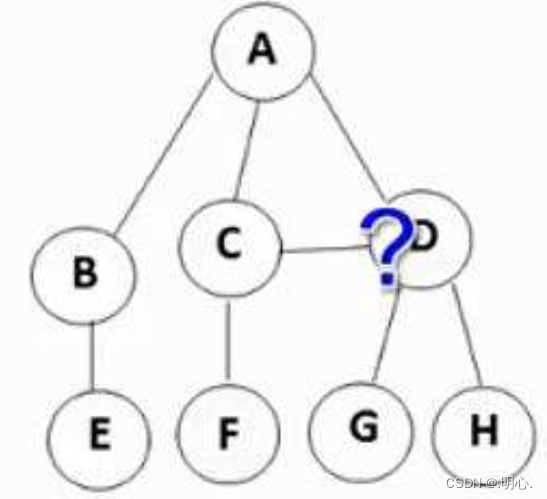
2. 与树相关的概念
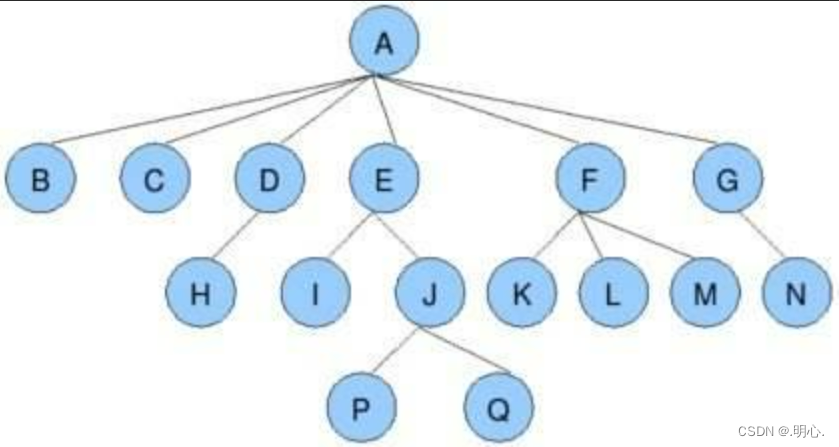
- 结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
- 树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
- 叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等节点为叶结点
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
- 根结点:一棵树中,没有双亲结点的结点;如上图:A
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
- 树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
二、二叉树
1.什么是二叉树
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
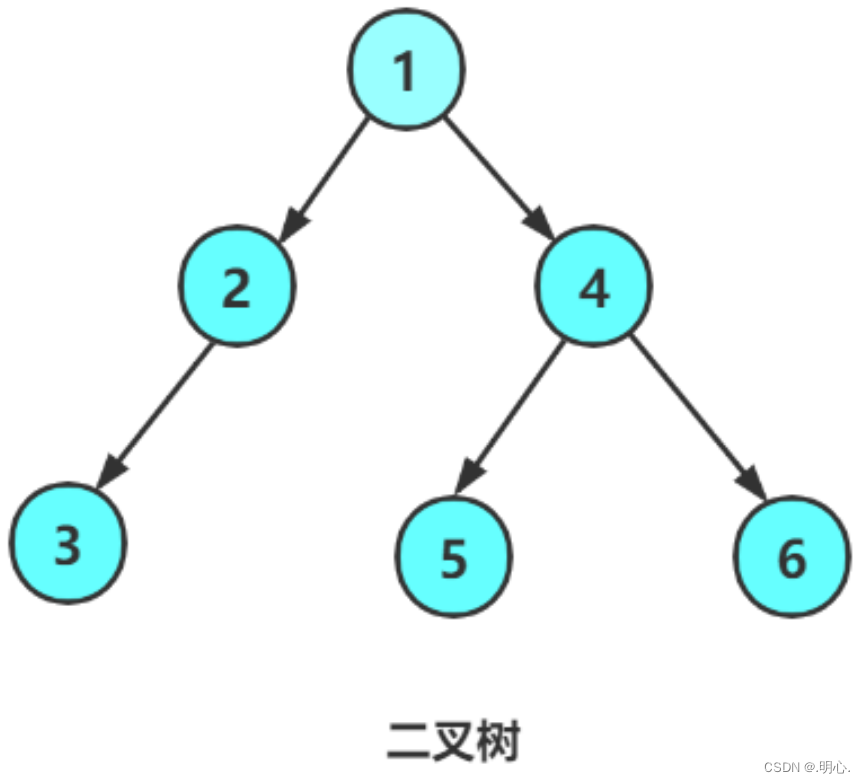
2.二叉树特点
- 二叉树不存在度大于2的结点(树的度:一棵树中,所有结点 度的最大值 称为树的度)
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
3.满二叉树与完全二叉树
- 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵又树的层数为K,且结点总数是2^k-1,则它就是满二叉树
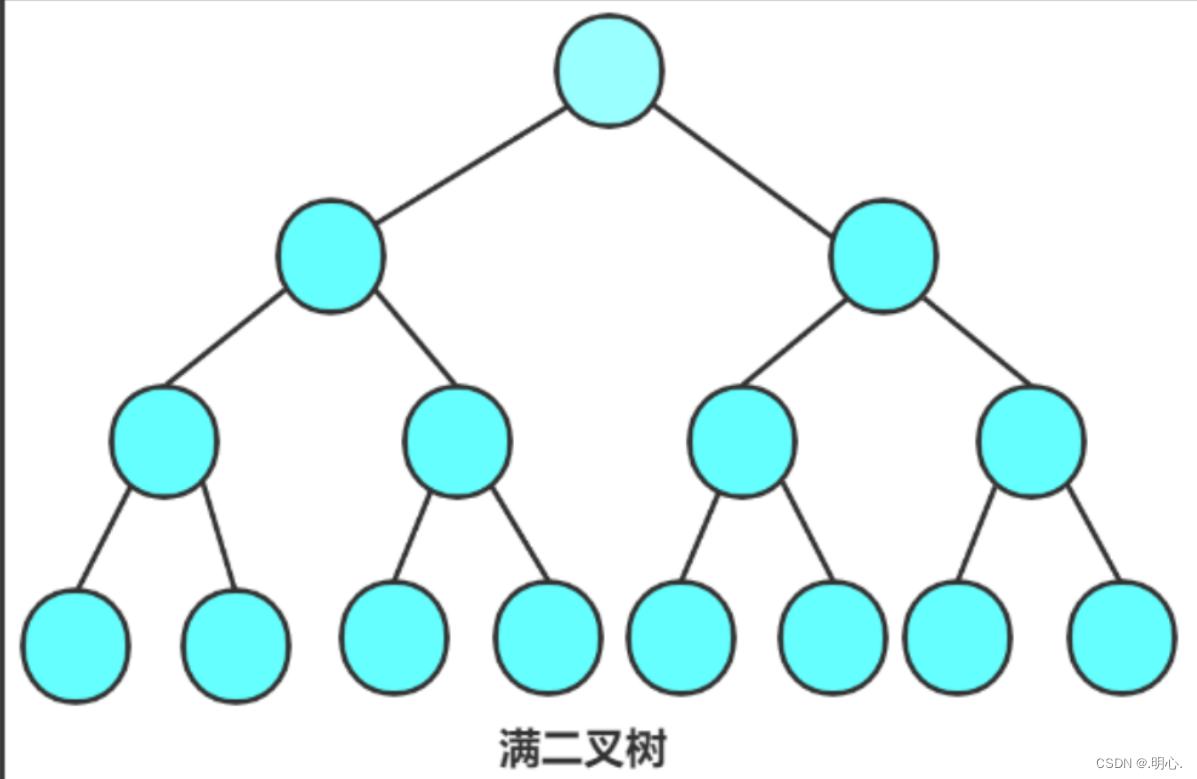
- 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一 一对应时称之为完全二叉树。 意思就是完全二叉树的所有节点从上到下,从左到右依次排满。 要注意的是满二叉树是一种特殊的完全二又树。
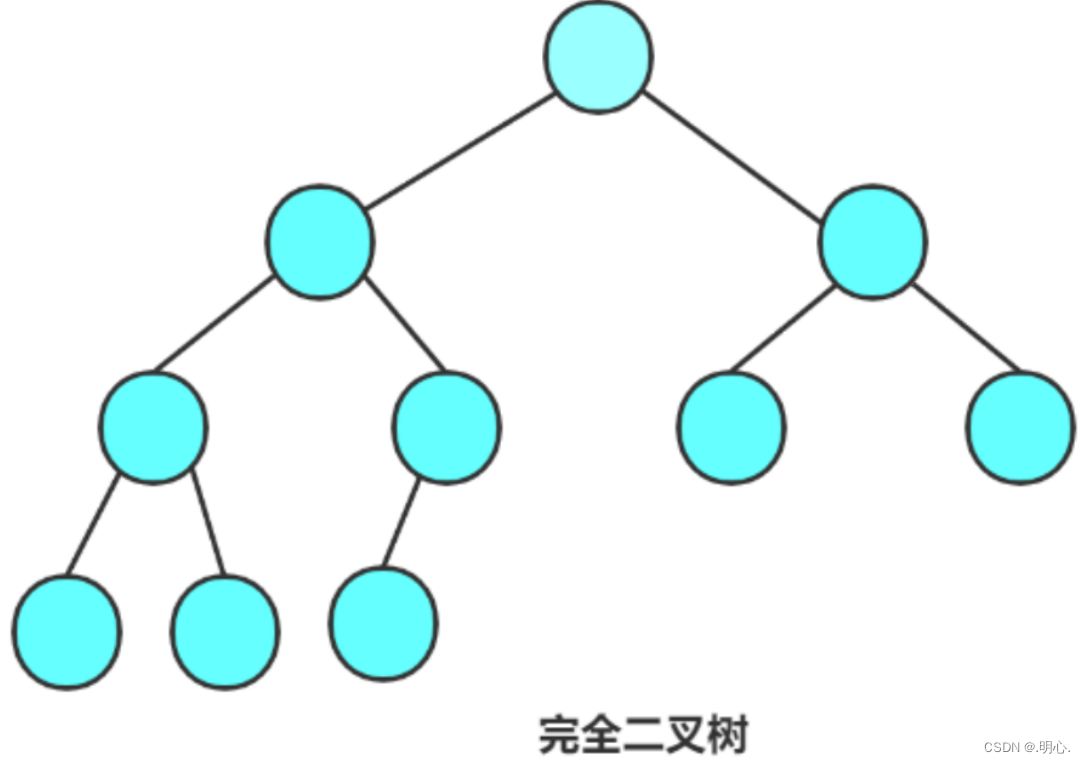
完全二叉树有一个特点,那就是如果总结点数为奇数,那么这个二叉树就只有一个度为1的节点,如果是偶数,就没有度为1的结点。
4.二叉树性质
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 (i>0)个结点
2. 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是(k>=0)
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
4. 具有n个结点的完全二叉树的深度k为上取整
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i 的结点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
相关题目:
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
3.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
答案:
1.B
解析:
叶子结点或终端结点:度为0的结点称为叶结点。
由前面说的二叉树性质第3点:对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1。所以 n2=199,n0=n2+1=200.
2.A
解析:
设结点总数为N=2n,因为题目中说了这是一颗完全二叉树,而结点总数是偶数,那么说明这个二叉树只有一个度为1的结点。
N=n0+n1+n2 => 2n=n0+n2+1 因为n0=n2+1,所以 2n-1=n0+n0-1 => n0=n
3.B
解析:
N=767,767为奇数,所以这个二叉树没有度为1的结点(n1=0)
N=n0+n1+n2=n0+n0-1=767 => n0=384
4.B
解析:
由前面说的二叉树性质第4点:具有n个结点的完全二叉树的深度k为l
上取整.
< 532 <
=> 9<
<10,因为是上取整,那么 k=10.
5.二叉树的存储
二叉树的存储结构分为:
顺序存储和类似于链表的链式存储。二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式(孩子表示法以及孩子双亲表示法)。
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}6.二叉树的遍历和基本操作
二叉树的遍历
1.前中后序遍历
- 前序遍历:根节点 左子树 右子树
- 中序遍历:左子树 根节点 右子树
- 后序遍历:左子树 右子树 根节点
2.层序遍历
自上而下,自左至右逐层访问树的结点的过程就是层序遍历
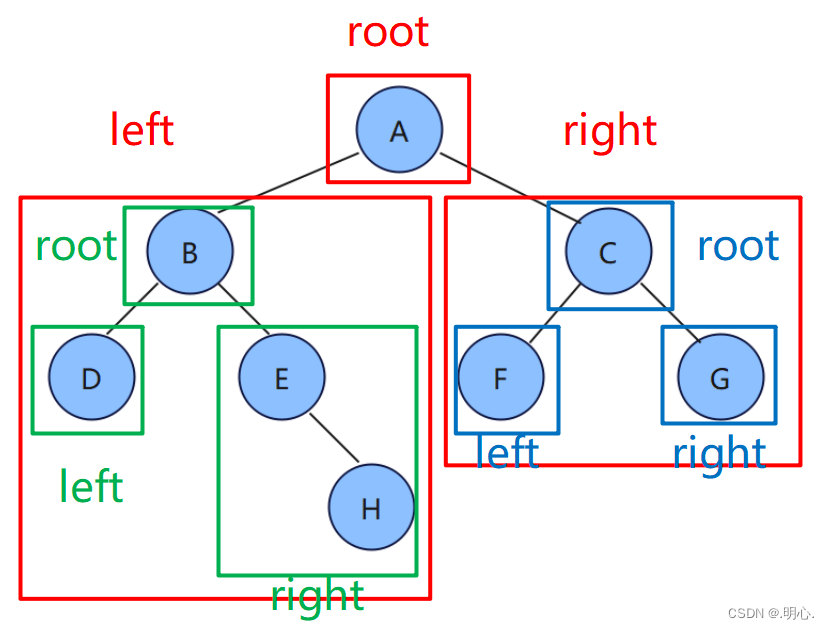
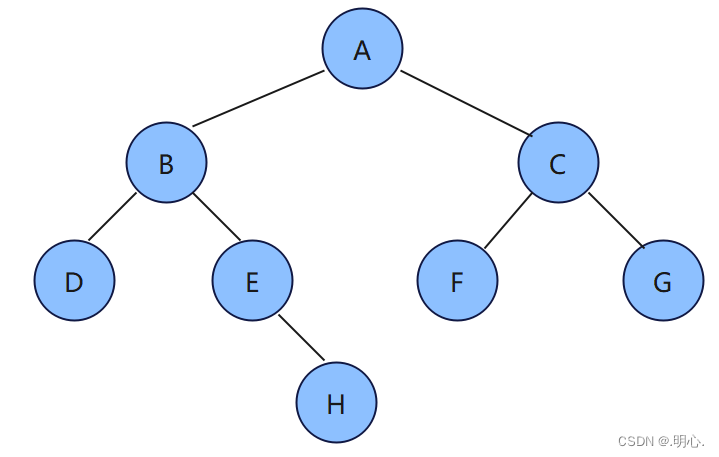
有如下二叉树,大家可用上述方法自行遍历
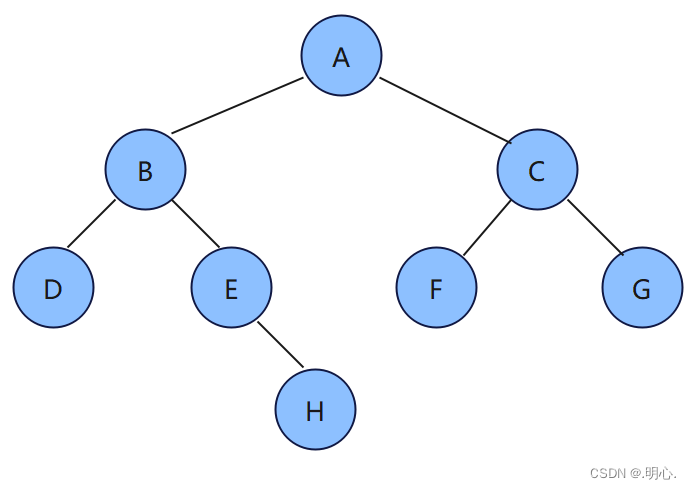
前序遍历:A B D E H C F G
中序遍历:D B E H A F C G
后序遍历:B D E H C F G A
层序遍历:A B C D E F G H
代码实现:
这里先按照上图用穷举的方式快速构建一颗二叉树(不是构建二叉树的正确方法)
public class BinaryTree {public static class TreeNode {TreeNode left;TreeNode right;char val;TreeNode(char val) {this.val = val;}}private TreeNode root;public TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');root = A;A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;return A;}//前序遍历public void preOrder(TreeNode root){if(root==null){return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}//中序遍历public void inOrder(TreeNode root){if (root==null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}//后序遍历public void postOrder(TreeNode root){if (root==null){return;}preOrder(root.left);preOrder(root.right);System.out.print(root.val+" ");}}public class Main {public static void main(String[] args) {BinaryTree binaryTree=new BinaryTree();BinaryTree.TreeNode root=binaryTree.createTree();System.out.print("前序遍历:");binaryTree.preOrder(root);System.out.println();System.out.print("中序遍历:");binaryTree.inOrder(root);System.out.println();System.out.print("后序遍历:");binaryTree.postOrder(root);}
}运行结果:

二叉树的基本操作
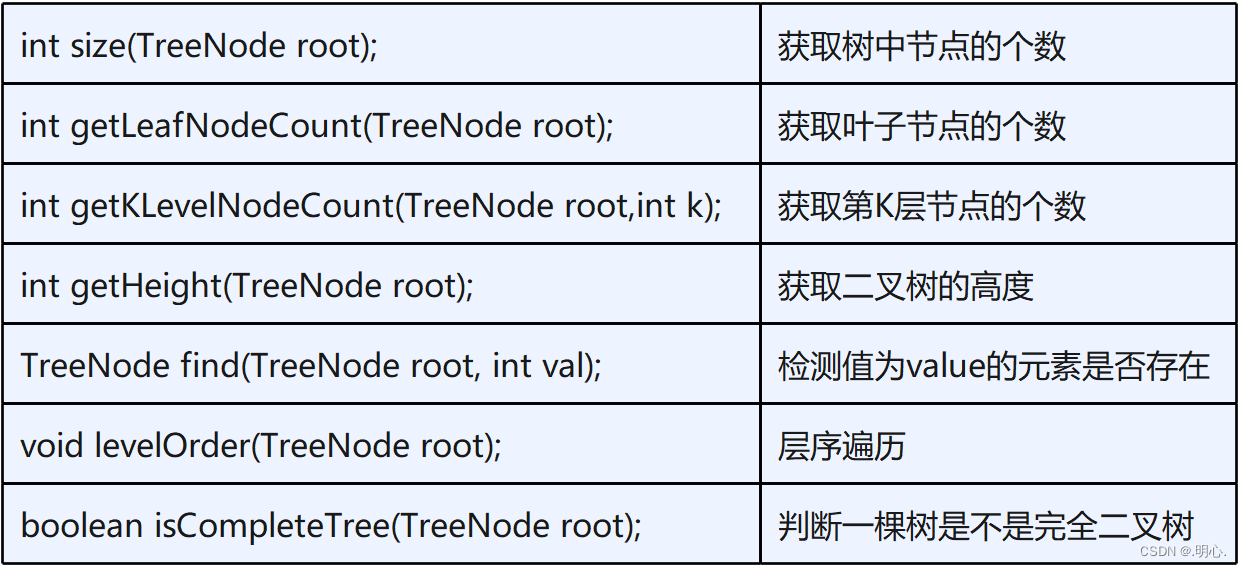
1. 获取树中节点的个数
这个方法实现在这里有两种思路:
1.遍历这个树,是结就nodeSize++
2.用子问题的思路来解决:总结点数=左子树结点的个数+右子树结点的个数+根结点
public static int nodeSize=0;//获取树中节点的个数(遍历每个节点)public void size(TreeNode root){if (root==null){return;}nodeSize++;size(root.left);size(root.right);}//用子问题的思路来解决:总节点数=左子树节点的个数+右子树节点的个数+根节点public int size2(TreeNode root){if (root==null){return 0;}int tmp=size2(root.left)+size2(root.right)+1;return tmp;}2.获取叶子节点的个数
叶子结点的特点就是度为0,即其左子树和右子树都是空。
这个方法实现在这里有两种思路:
1.遍历这个树,只要root不为空且root的左子树和右子树都为空,就说明root所在的结点是叶子结点
2.用子问题的思路来解决:总叶子结点数=左子树的叶子结点+右子树的叶子结点
public int leafSize;public void getLeafNodeCount(TreeNode root) {if(root == null) {return;}if(root.left == null && root.right == null) {leafSize++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);}//子问题思路:这颗树的总叶子结点数=左子树的叶子结点+右子树的叶子结点public int getLeafNodeCount2(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {return 1;}return getLeafNodeCount2(root.left)+ getLeafNodeCount2(root.right);}3.获取第K层节点的个数
public int getKLevelNodeCount(TreeNode root,int k){if (root==null){return 0;}if (k==1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}4.获取二叉树的高度
整棵树的高度=找出 左子树的高度 和 右子树的高度 的最大值 +1(树的高度或深度:树中结点的最大层次)
// 获取二叉树的高度public int getHeight(TreeNode root){if(root==null){return 0;}int leftHeight=getHeight(root.left);int rightHeight=getHeight(root.right);return Math.max(leftHeight,rightHeight)+1;}
5. 检测值为value的元素是否存在
1.先判断根节点的值是不是我们要找的value,如果是就返回这个root
2.如果当前根节点不是我们要找的value,那就到当前根节点的左子树去找,如果左子树找不到就去右子树找。
// 检测值为value的元素是否存在private TreeNode find(TreeNode root, int val){if (root==null){return null;}if (root.val==val){System.out.println(root.val);return root;}TreeNode leftval=find(root.left,val);if(leftval!=null){return leftval;}TreeNode rightval=find(root.right,val);if (rightval!=null){return rightval;}return null;}6.层序遍历
先入队根节点,然后出队,若当前根节点左右不为空,则把不为空的左右入队,出新的队头,以此类推。
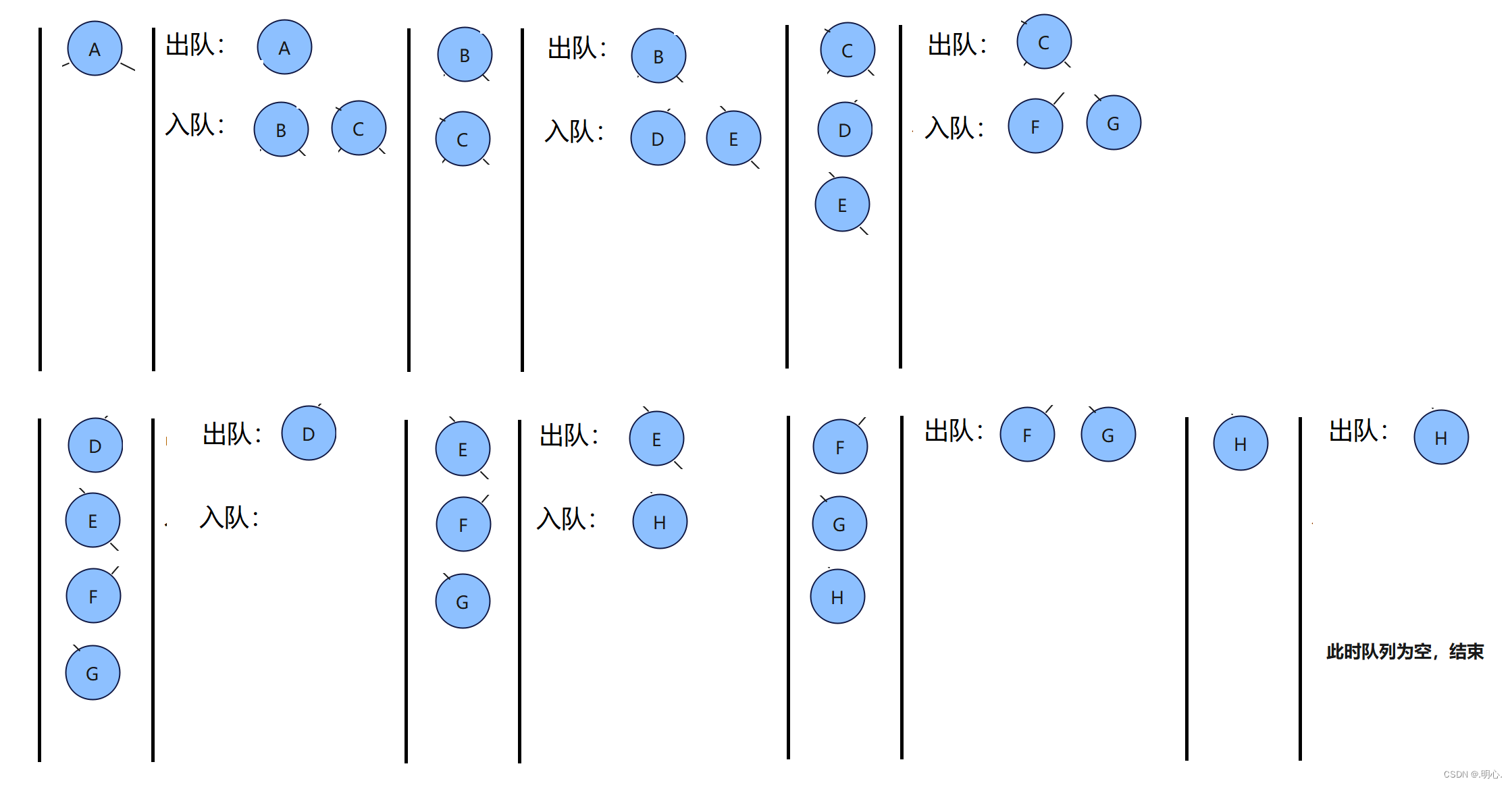
public void levelOrder(TreeNode root) {if(root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();System.out.print(cur.val+" ");if(cur.left != null) {queue.offer(cur.left);}if(cur.right != null) {queue.offer(cur.right);}}}7.判断一棵树是不是完全二叉树
1.先把根节点放到队列当中
2.队列不为空,弹出元素,带入左右(可以为空)
3.当队列弹出元素为null则停止
4.最后一步,判断当前队列是否元素都是nul,只要出现不为nul的元素,则当前二又树不是完全二叉树
public boolean isCompleteTree(TreeNode root) {if(root == null) return true;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();if(cur != null) {queue.offer(cur.left);queue.offer(cur.right);}else {break;//结束之后 遍历队列剩下的所有元素 是不是都是null}}// 遍历队列剩下的所有元素 是不是都是nullwhile (!queue.isEmpty()) {TreeNode cur = queue.poll();if(cur != null) {return false;}}return true;}相关文章:

初识二叉树和二叉树的基本操作
目录 一、树 1.什么是树 2. 与树相关的概念 二、二叉树 1.什么是二叉树 2.二叉树特点 3.满二叉树与完全二叉树 4.二叉树性质 相关题目: 5.二叉树的存储 6.二叉树的遍历和基本操作 二叉树的遍历 二叉树的基本操作 一、树 1.什么是树 子树是不相交的;…...

如何开辟动态二维数组(C语言)
1. 开辟动态二维数组 C语言标准库中并没有可以直接开辟动态二维数组的函数,但我们可以通过动态一维数组来模拟动态二维数组。 二维数组其实可以看作是一个存着"DataType []"类型数据的一维数组,也就是存放着一维数组地址的一维数组。 所以&…...
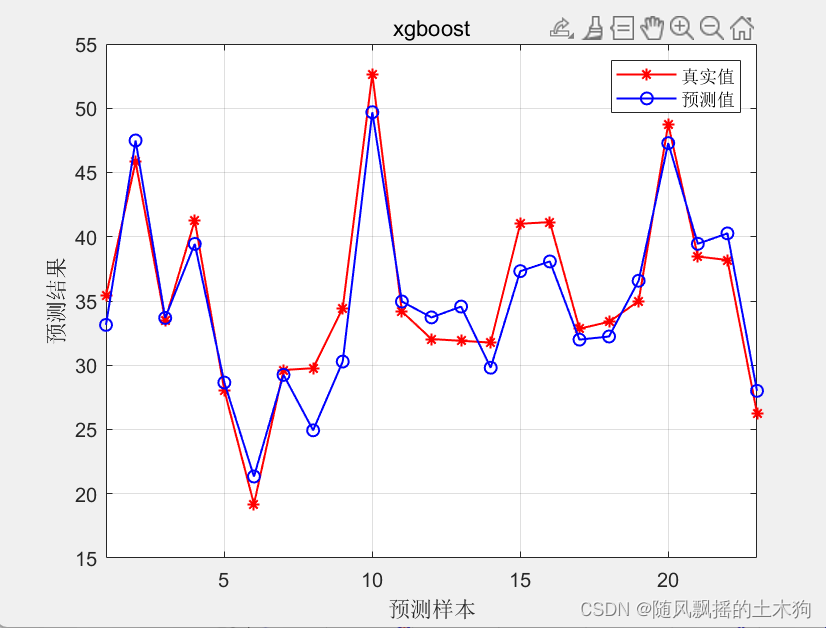
【MATLAB第104期】基于MATLAB的xgboost的敏感性分析/特征值排序计算(针对多输入单输出回归预测模型)
【MATLAB第104期】基于MATLAB的xgboost的敏感性分析/特征值排序计算(针对多输入单输出回归预测模型) 因matlab的xgboost训练模型不含敏感性分析算法,本文通过使用single算法,即单特征因素对输出影响进行分析,得出不同…...

C语言程序与设计——工程项目开发
之前我们已经了解了C语言的基础知识部分,掌握这些之后,基本就可以开发一些小程序了。在开发时,就会出现合作的情况,C语言是如何协作开发的呢,将在这一篇文章进行演示。 工程项目开发 在开发过程中,你接到…...

【Java核心技术】第6章 接口
1 接口 接口不是类,而是对希望符合这个接口的类的一组需求 1.1 Comparable 接口 要对对象进行比较,就要实现(implement)比较(comparable)接口 注意: implements Comparable<Manager> Comparable接口是泛型接口 class Manager exten…...

【Java探索之旅】从输入输出到猜数字游戏
🎥 屿小夏 : 个人主页 🔥个人专栏 : Java编程秘籍 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一、输入输出1.1 输出到控制台1.2 从键盘输入 二、猜数字游戏2.1 所需知识:…...

【动态规划】【01背包】Leetcode 1049. 最后一块石头的重量 II
【动态规划】【01背包】Leetcode 1049. 最后一块石头的重量 II 解法 ---------------🎈🎈题目链接🎈🎈------------------- 解法 😒: 我的代码实现> 动规五部曲 ✒️确定dp数组以及下标的含义 dp[j]表示容量为…...

2023 年上海市大学生程序设计竞赛 - 四月赛
A. 宝石划分 A. 宝石划分 - 2023 年上海市大学生程序设计竞赛 - 四月赛 - ECNU Online Judge 找距离N最近的M的因数q,输出M/q 如果是暴力所的话,会超时 #include <bits/stdc.h> using namespace std; int main(){ios::sync_with_stdio(false)…...

别让这6个UI设计雷区毁了你的APP!
一款成功的APP不仅仅取决于其功能性,更取决于用户体验,这其中,UI设计又至关重要。优秀的UI设计能够为用户带来直观、愉悦的交互体验,甚至让用户“一见钟情”,从而大大提高产品吸引力。 然而,有很多设计师在…...

继承【C/C++复习版】
目录 一、什么是继承?怎么定义继承? 二、继承关系和访问限定符? 三、基类和派生类对象可以赋值转换吗? 四、什么是隐藏?隐藏vs重载? 五、派生类的默认成员函数? 1)派生类构造函…...

题目 2694: 蓝桥杯2022年第十三届决赛真题-最大数字【暴力解法】
最大数字 原题链接 🥰提交结果 思路 对于每一位,我我们都要尽力到达 9 所以我们去遍历每一位, 如果是 9 直接跳过这一位 如果可以上调到 9 我们将这一位上调到 9 ,并且在a 中减去对应的次数 同样的,如果可以下调到 9,我…...

【C语言】- C语言字符串函数详解
C语言字符串函数详解 1、void *memset(void *dest, int c, size_t count); 将dest前面count个字符置为字符c. 返回dest的值. 2、void *memmove(void *dest, const void *src, size_t count); 从src复制count字节的字符到dest. 如果src和dest出现重叠, 函数会自动处理. 返回…...
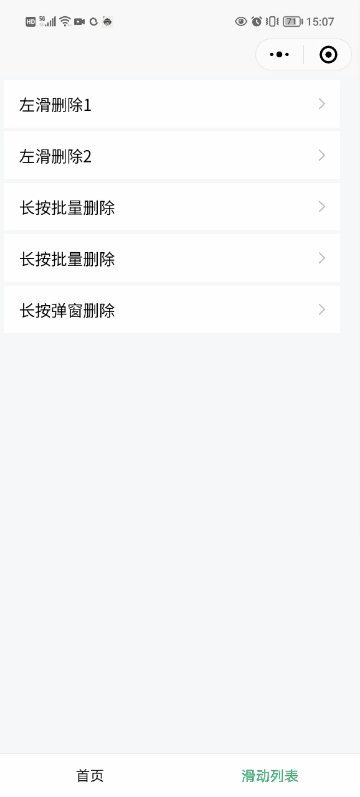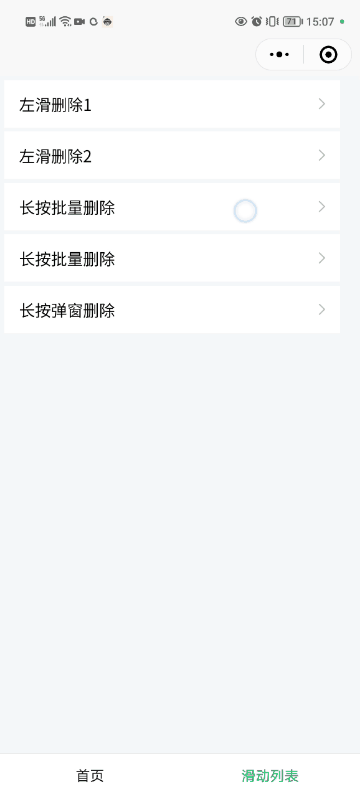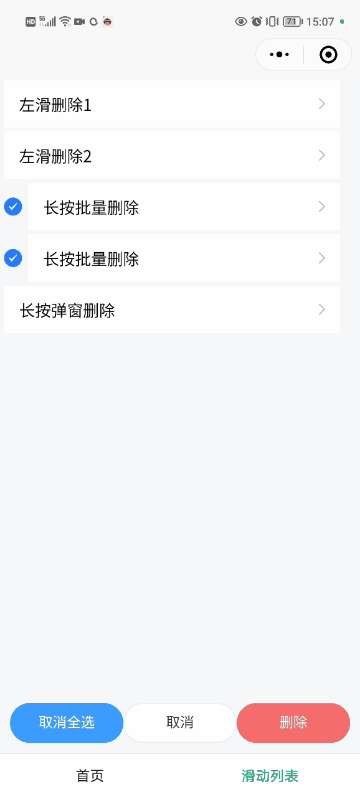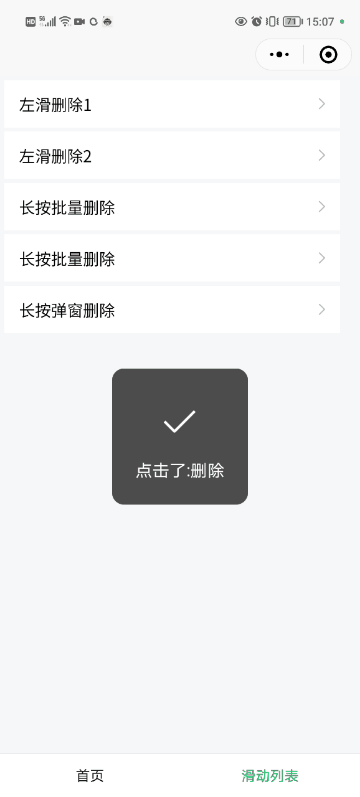
如何实现小程序滑动删除组件+全选批量删除组件
如何实现小程序滑动删除组件全选批量删除组件 一、简介 如何实现小程序滑动删除组件全选批量删除组件 采用 uni-app 实现,可以适用微信小程序、其他各种小程序以及 APP、Web等多个平台 具体实现步骤如下: 下载开发者工具 HbuilderX进入 【Dcloud 插…...

基于SSM+Jsp+Mysql的农产品供销服务系统
开发语言:Java框架:ssm技术:JSPJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包…...

网络编程学习探索系列之——广播原理剖析
hello !大家好呀! 欢迎大家来到我的网络编程系列之广播原理剖析,在这篇文章中, 你将会学习到如何在网络编程中利用广播来与局域网内加入某个特定广播组的主机! 希望这篇文章能对你有所帮助,大家要是觉得我写…...

小程序开发SSL证书下载和安装
在开发小程序时,确保数据的安全传输至关重要,而实现这一目标的关键在于正确获取与安装SSL证书。以下详细介绍了从获取到安装SSL证书的完整流程,以助您为小程序构建可靠的加密通信环境。 一、小程序SSL证书类型选择: 域名验证型D…...

医疗图像分割 | 基于Pyramid-Vision-Transformer算法实现医疗息肉分割
项目应用场景 面向医疗图像息肉分割场景,项目采用 Pytorch Pyramid-Vision-Transformer 深度学习算法来实现。 项目效果 项目细节 > 具体参见项目 README.md (1) 模型架构 (2) 项目依赖,包括 python 3.8、pytorch 1.7.1、torchvision 0.8.2(3) 下载…...

蓝桥杯 每日2题 day5
碎碎念:哦哈呦,到第二天也是哦哈哟,,学前缀和差分学了半天!day6堂堂连载! 0.单词分析 14.单词分析 - 蓝桥云课 (lanqiao.cn) 关于这题就差在input前加一个sorted,记录一下下。接下来就是用字…...

[ 云计算 | AWS 实践 ] Java 应用中使用 Amazon S3 进行存储桶和对象操作完全指南
本文收录于【#云计算入门与实践 - AWS】专栏中,收录 AWS 入门与实践相关博文。 本文同步于个人公众号:【云计算洞察】 更多关于云计算技术内容敬请关注:CSDN【#云计算入门与实践 - AWS】专栏。 本系列已更新博文: [ 云计算 | …...
循环单链表算法库
学习贺老师数据结构 数据结构之自建算法库——循环单链表_循环单链表 csdn-CSDN博客 整理总结出的循环单链表算法库 v1.0 : 基本实现功能 v2.0(2024.4.6): 修复Delete_SpecificLocate_CyclicList()删除节点函数bug,添加验证删除节点是否超范围判断 目录 1.主要功能…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
