纯小白蓝桥杯备赛笔记--DAY4(数学数据结构图论)
文章目录
- 数学
- 质因数分解
- 辗转相除法求最大公约数
- 最小公倍数:
- 快速幂
- 乘法逆元
- 费马小定理
- 逆元
- 乘法逆元
- 素数判定与埃式筛法
- 朴素素数判定法
- 埃式筛法
- 图论
- 并查集T3:真题--合根植物
- Dijkstra
- Floyd
- 基础算法
- 递归,循环,前缀和,差分
- STL
数学
质因数分解
int reduce(int prime[],int pn,int n,int rest[]){int i,k=0;for(i=0;i<pn;i++){if (n==1) break;if (prime[i]*prime[i]>n) {rest[k++]=n;break;}while(n%prime[i]==0){n/=prime[i];rest[k++]=prime[i];}}return k;}
解析:
这段代码是一个名为reduce的函数,它接受四个参数:一个整数数组prime[],一个整数pn表示数组的长度,一个整数n和一个整数数组rest[]。函数的目的是将整数n分解为质因数,并将这些质因数存储在rest[]数组中。
函数首先初始化两个变量i和k,其中i用于循环遍历prime[]数组,k用于记录rest[]数组的索引。
接下来,函数使用一个for循环遍历prime[]数组。在每次迭代中,它首先检查n是否等于1,如果是,则跳出循环。然后,它检查当前质数的平方是否大于n,如果是,则将n添加到rest[]数组中,并跳出循环。
如果当前质数的平方不大于n,则进入一个while循环。在这个循环中,只要n能被当前质数整除,就将n除以当前质数,并将当前质数添加到rest[]数组中。这个过程会一直重复,直到n不能被当前质数整除为止。
最后,函数返回k,即rest[]数组中的元素个数。
#include<bits/stdc++.h>
using namespace std;int main()
{int n,i;cin>>n;cout<<n<<"=";for(i=2;i<=n;i++){while(n!=i){if(n%i==0){cout<<i<<"*";n=n/i;}elsebreak;}}cout<<n<<endl;return 0;
}
辗转相除法求最大公约数
inline int gcd(int a,int b)
{if(a%b==0)return b;elsereturn (gcd(b,a%b));
}
- 简单写法:
int gcb(int a,int b){return b==0 ? a:gcb(b,a%b);}
最小公倍数:
int lcm(int a,int b){return a/gcd(a,b)*b;//防溢出 , 很妙啊 ,大家可以记一下
}
快速幂

- 模板
int qmi(int a,int b,int p)//对p取模
{int res=1;while(b)//只要b不为0,就一直迭代下去 {if(b&1)res=res*a%p;//b为奇数,乘一个a到答案里a=a*a%p,b>>=1;//底数平方,指数除以2 }return res; }
- 例题:数的幂次–1181
#include<bits/stdc++.h>
using namespace std;using ll =long long;ll qmi(ll a,ll b,ll p)//对p取模
{ll res=1;while(b)//只要b不为0,就一直迭代下去 {if(b&1)res=res*a%p;//b为奇数,乘一个a到答案里a=(ll)a*a%p,b>>=1;//底数平方,指数除以2 }return res; } int main(){int t;cin>>t;while(t--){ll n,m,p;cin>>n>>m>>p;cout<<qmi(n,m,p)<<endl;}return 0;}
乘法逆元
费马小定理

逆元

乘法逆元
- 例题1:求乘法逆元
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
int t,n;
ll p=1e9+7;
ll qsm(ll a,ll b)
{ll res=1;while(b){if(b&1) res=res*a%p;a=a*a%p;b>>=1;}return res%p;
}
ll inv(ll x)
{return qsm(x,p-2);
}
int main()
{cin>>t;while(t--){cin>>n;cout<<inv(n)<<endl;}return 0;
}- 例题2:获胜的概率–3932
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p=1e9+7;
ll kmi(ll a,ll b)
{ll res=1;while(b){if(b&1) res=res*a%p;a=a*a%p;b>>=1;}return res%p;}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);ll n,k;cin>>n>>k;if(k==0){cout<<1<<endl;for(int i=2;i<=n;i++) cout<<0<<endl;}else if(k&1){for(int i=1;i<=n;i++){if(i&1) cout<<0<<endl;else cout<<kmi(n/2,p-2)<<endl;}}else{for(int i=1;i<=n;i++){if(i&1) cout<<kmi((n+1)/2,p-2)<<endl;else cout<<0<<endl;}}return 0;}素数判定与埃式筛法
朴素素数判定法

- 例题:疑似素数-3334
#include<bits/stdc++.h>
using namespace std;
//求和
int f(int x)
{int res=0;while(x)res+=x%10,x/=10;return res;}
bool isPrime(int n)
{if(n<2)return false;for(int i=2;i<=n/i;i++){if(n%i==0)return false;}return true;}
int main()
{int n;cin>>n;int ans=0;for(int i=1;i<=n;i++){if(isPrime(f(i)))ans++;}cout<<ans<<endl;
}
埃式筛法
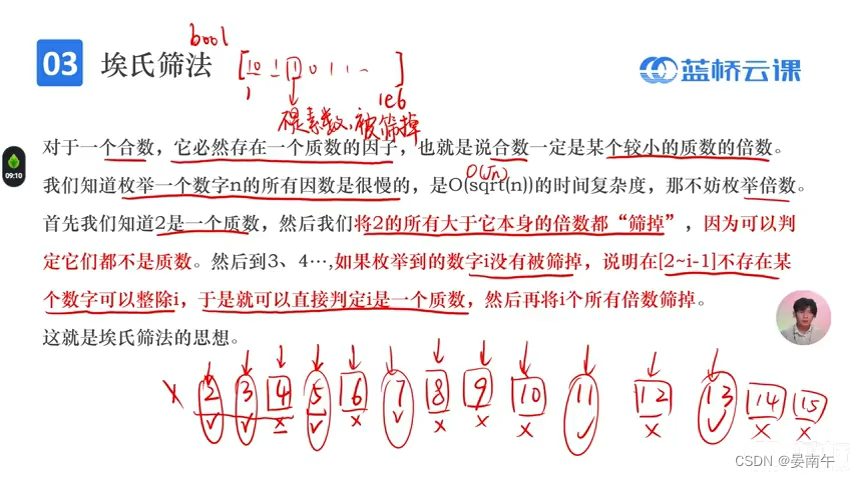
bool vis[N];
vis[0]=vis[1]=true;//被筛掉了
for(int i=2;i<=n;i++)
{if(!vis[i])//如果i没有被筛掉,那么进行枚举for(int j=2*i;j<=n;j+=i)//枚举倍数 ,每次j变成i的倍数vis[j]=ture; }
- 例题2:小明的素数对–3205
#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
bool shai[N];vector<int> vec;//将素数筛中杂乱的质数变成排列有序的一个集合,用vector
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,ans=0;cin>>n;shai[0]=shai[1]=1;for(int i=2;i<=n;i++){if(!shai[i]){vec.push_back(i);for(int j=2*i;j<=n;j+=i) shai[j]=1;}}for(int i=0;i<vec.size();i++)for(int j=i+1;j<vec.size();j++){if(!shai[vec[j]-vec[i]]) ans++;}cout<<ans;return 0;}图论
并查集T3:真题–合根植物
- 并查集模版题:
- 注意:不要调用string库。
- 什么是并查集:处理不相交集合的合并问题。
- 用途:求连通子图,求最小生成树的Kruskal算法和求最近公共祖先等。
- 操作:
-
初始化:

-
查询与合并:

-
查询时对路径进行压缩:
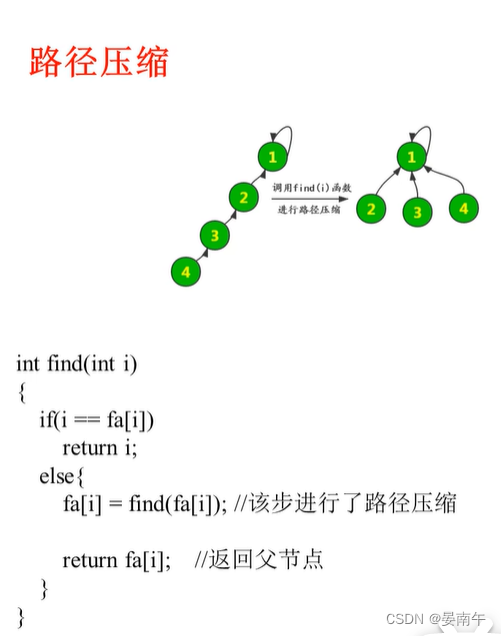
-
例题

-
#include<cstdio>
#include<cstdlib>
using namespace std;
// 开始的时候定义数组
#define MAXN 20001
int fa[MAXN];
//最好不要这样定义// 初始化
void init(int n)
{for(int i=0;i<=n;i++)fa[i]=i;}
// 查询 int find(int x){
// 递归出口if(x==fa[x])return x;else{fa[x]==find(fa[x]);return fa[x];}}
// 合并
void unionn(int i,int j)
{int i_fa=find(i);// 找到i的祖先 int j_fa=find(j);// 找到j的祖先 fa[i_fa]=j_fa ;//i的祖先指向j的祖先 }
// 写主函数
int main()
{int m,n,x,y,q;scanf("%d",&n);init(n);// 初始化这个数组scanf("%d",&m); //有m行for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);unionn(x,y);} scanf("%d",&q);// 输入q行 for(int i=1;i<=q;i++){scanf("%d%d",&x,&y);if(find(x)==find(y))printf("YES\n");elseprintf("NO\n");}return 0; }
- 合根植物题解:这道题只有一个返回值,所以查询的时候注意不要增加一个返回值了。
#include<stdio.h>
int fa[1000005];
//初始化void init(int n){for (int i=1;i<=n;i++)fa[i] = i;}// 查询
int find(int x)
{if (fa[x] != x){int sx = find(fa[x]);fa[x] = sx;}return fa[x];
}// 合并void unionn(int i,int j){int i_fa=find(i);int j_fa=find(j);fa[i_fa]=j_fa;}
int main(void)
{int m,n,q;scanf("%d%d%d",&m,&n,&q);init(m*n); int x,y;for(int i=0;i<q;i++){scanf("%d%d",&x,&y);unionn(x,y);}//计数器的设置int ans=0;for(int i=1;i<=m*n;i++){if(i==fa[i]){//一个数等于链条的祖先ans++; } }printf("%d\n",ans);return 0;
}
Dijkstra


Floyd

基础算法
递归,循环,前缀和,差分
添加链接描述
STL
添加链接描述

相关文章:

纯小白蓝桥杯备赛笔记--DAY4(数学数据结构图论)
文章目录 数学质因数分解辗转相除法求最大公约数最小公倍数:快速幂乘法逆元费马小定理 逆元乘法逆元素数判定与埃式筛法朴素素数判定法埃式筛法 图论并查集T3:真题--合根植物DijkstraFloyd 基础算法递归,循环,前缀和,差分STL 数学…...

python 最简单的网页爬虫
import requests url"https://news.ifeng.com/c/8OZc7eV01sM" rrequests.get(url) print(r.status_code) print(r.iter_lines()) # 获取响应的内容 content r.text# 打印网页内容 print(content) # responser.json() # print(response) 爬虫知识讲解: …...

二叉树-数据结构
二叉树-数据结构 二叉树是属性结构的一个重要类型。 如下图二叉树形状 二叉树特征如下: 1.二叉树由 n(n > 0) 个节点组成 2.如果 n 为 0,则为空树 3.如果 n 1,则只有一个节点称为根节点(root) 4.每个节点最多有两个节点,节…...

ansible使用shell模块的环境变量问题
在本机写了一个shell脚本,关于操作mysql的,在本机执行脚本可以正常操作数据库,脚本运行正常。 但是使用ansible ansible -i ./hosts test_teledb -m copy -a "src/etc/ansible/scripts/check.sh dest/tmp"ansible -i ./hosts test…...

ChatGPT论文写作指南:写出引人注目的论文
ChatGPT无限次数:点击直达 ChatGPT论文写作指南:写出引人注目的论文 作为一名有着10年经验的专业CSDN网站原创文章优质创作者,在当今的信息爆炸时代,论文写作的重要性愈发显现。如何能够写出引人注目的论文,吸引读者的眼球并获得…...
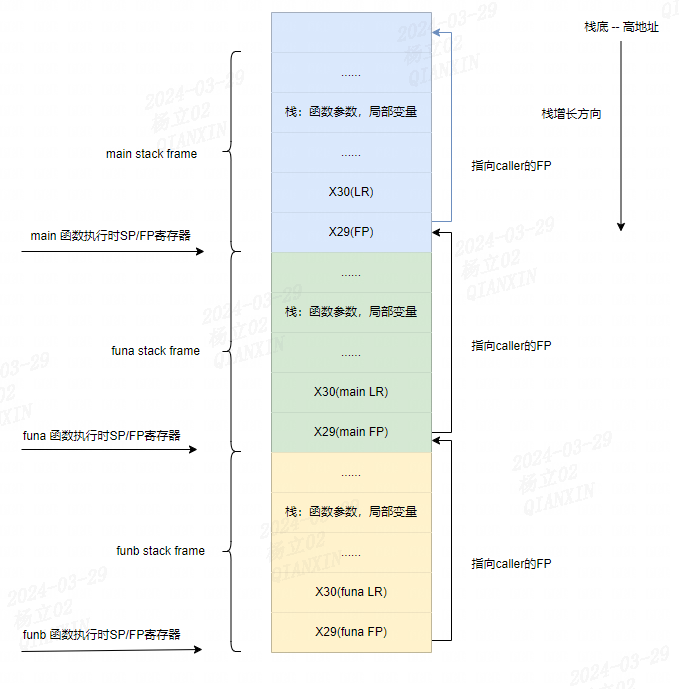
ARM64架构栈帧回溯
文章目录 前言一、栈帧简介二、demo演示 前言 请参考:ARM64架构栈帧以及帧指针FP 一、栈帧简介 假设下列函数调用: funb() {func() }funa() {funb() }main() {funa() }main函数,funa函数,funb函数都不是叶子函数,其…...
-- 基础知识)
LangChain:大型语言模型(LLMs)-- 基础知识
1、LangChain的调用大型语言模型模块的介绍 LangChain是一个强大的框架,旨在通过调用大型语言模型(LLM)来开发各种语言驱动的应用程序。在LangChain中,LLM不仅仅是一个简单的模型调用,而是一个复杂链条中的关键部分。…...

总分410+专业130+国防科技大学831信号与系统考研经验国防科大电子信息与通信工程,真题,大纲,参考书。
好几个学弟催着,总结一下我自己的复习经历,希望大家复习少走弯路,投入的复习正比换回分数。我专业课831信号与系统130(感觉比估分要低,后面找Jenny老师讨论了自己拿不准的地方也没有错误,心里最近也这经常回…...

chatgpt Team 4.0共享合租账号的新方式
为了更好地满足工作需求,我订阅了GPT PLUS会员,但我发现,4.0每三小时问答40次经常吃灰,而且每月近200元的费用让我感到有点肉痛。 于是,我开始寻找有没有什么替代品。在逛某论坛的时候,发现了一个共享Team…...

类和对象二
一、运算符重载 为了使自定义类型可以使用加减等运算符,CPP提供了一个功能叫运算符重载。 关键字:operator操作符 运算符重载最好定义在类对象里,这也可以避免访问不到私有成员的问题。 代码演示: 在类里定义之后,…...

GD32 HID键盘矩阵键盘发送数据时,一直发送数据问题处理
这个问题找了两三天,开始并不认为是示例程序的问题,只是感觉是自己代码问题。 这个解决流程大概是: 先调好矩阵键盘=> 调用发送函数。 就是因为调用时,一直发送数据,我也在按键抬起做了操作,始终不行。 最后,发现时示例代码中有个 空闲中断 引起的。 udev->reg…...

小程序地理位置权限申请+uniapp调用uni.getLocation
文章目录 一、小程序地理位置权限申请二、uniapp调用uni.getLocation 一、小程序地理位置权限申请 需要确保小程序类目已经填写 点击左侧导航栏找到最后的“设置”——“基本设置”——“前往填写” 在开发管理——接口设置——地理位置中可以看到: 即可点击想要申…...

后台权限控制及动态路由
需求 后台系统需要能实现不同的用户权限可以看到不同的功能。 用户只能使用他的权限所允许使用的功能。 功能设计 之前在我的SpringSecurity的课程中就介绍过RBAC权限模型。没有学习过的可以去看下 RBAC权限模型 。这里我们就是在RBAC权限模型的基础上去实现这个功能。 表分…...

云计算:Linux 部署 OVS 集群(控制端)实现OpenFlow
目录 一、实验 1.环境 2.Linux 部署 OVS 集群(控制端) 3.控制端对接服务端OVS网元 4.服务端OVS添加流表 5.服务端删除OVS 二、问题 1. ODL如何查找已安装插件 2.查看流表显示不全 3.如何删除OVS流表 一、实验 1.环境 (1) 主机 表1 宿主机 主…...

使用/api/put保存数据到OpenTSDB,报204错误
错误信息 HttpResponseProxy{HTTP/1.1 204 No Content [Content-Type: application/json; charsetUTF-8, Content-Length: 0]} 错误原因 在OpenTSDB中,使用/api/put保执行写入操作,得到204响应,表示已经成功写入数据库。...
)
Open3D kmeans聚类(马氏距离,Python版本)
文章目录 一、简介二、算法步骤三、代码实现四、实现效果参考资料一、简介 在诸多的聚类方法中,K-Means聚类方法是属于“基于原型的聚类”(也称为原型聚类)的方法,此类方法均是假设聚类结构能通过一组原型刻画,在现实聚类中极为常用。通常情况下,该类算法会先对原型进行初始…...

python抠图程序
import cv2 import numpy as np def color_threshold(image, lower, upper): hsv_image cv2.cvtColor(image, cv2.COLOR_BGR2HSV) mask cv2.inRange(hsv_image, lower, upper) result cv2.bitwise_and(image, image, maskmask) return result # 读取图片…...
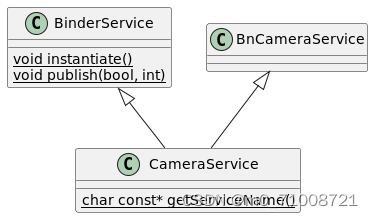
Android13 CameraServer启动流程
代码入口 frameworks/av/camera/cameraserver 里面包含了四个文件 我们先来看看Android.bp的内容 package {// See: http://go/android-license-faq// A large-scale-change added default_applicable_licenses to import// all of the license_kinds from "frameworks_a…...

如何升级node.js版本
升级Node.js可以通过多种方式来完成,以下是四种常见的方法: 方法一:使用Node.js官方安装程序 访问Node.js的官方网站,下载对应你操作系统的最新版本安装程序。通常,你可以 https://nodejs.org/en/download 找到你需…...
Excel---一个工作簿中的多个sheet合并成一个PDF
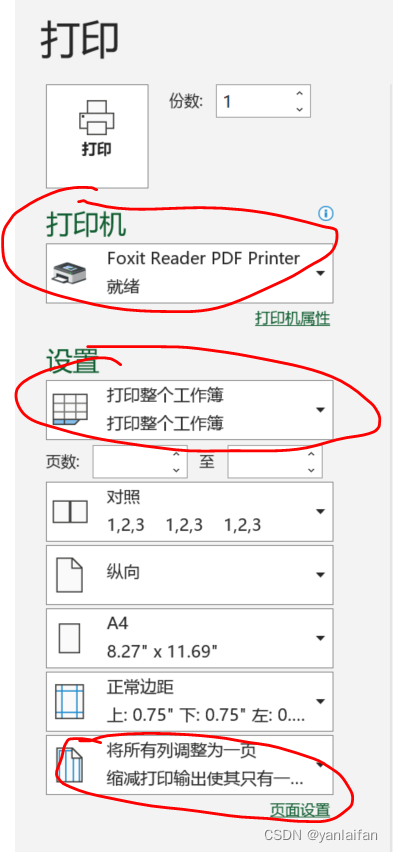
0 Preface/Foreword 1 操作方法 1.1 方法一 文件》 导出 》创建PDF/XPS 》 选项 》发布内容 》“整个工作簿” 1.2 方法二 文件》 打印》 打印机选项中,选择一种PDF阅读器 》设置选项中,选择打印整个工作簿。...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
