第十三届蓝桥杯真题:x进制减法,数组切分,gcd,青蛙过河
目录
x进制减法
数组切分
gcd
青蛙过河
x进制减法

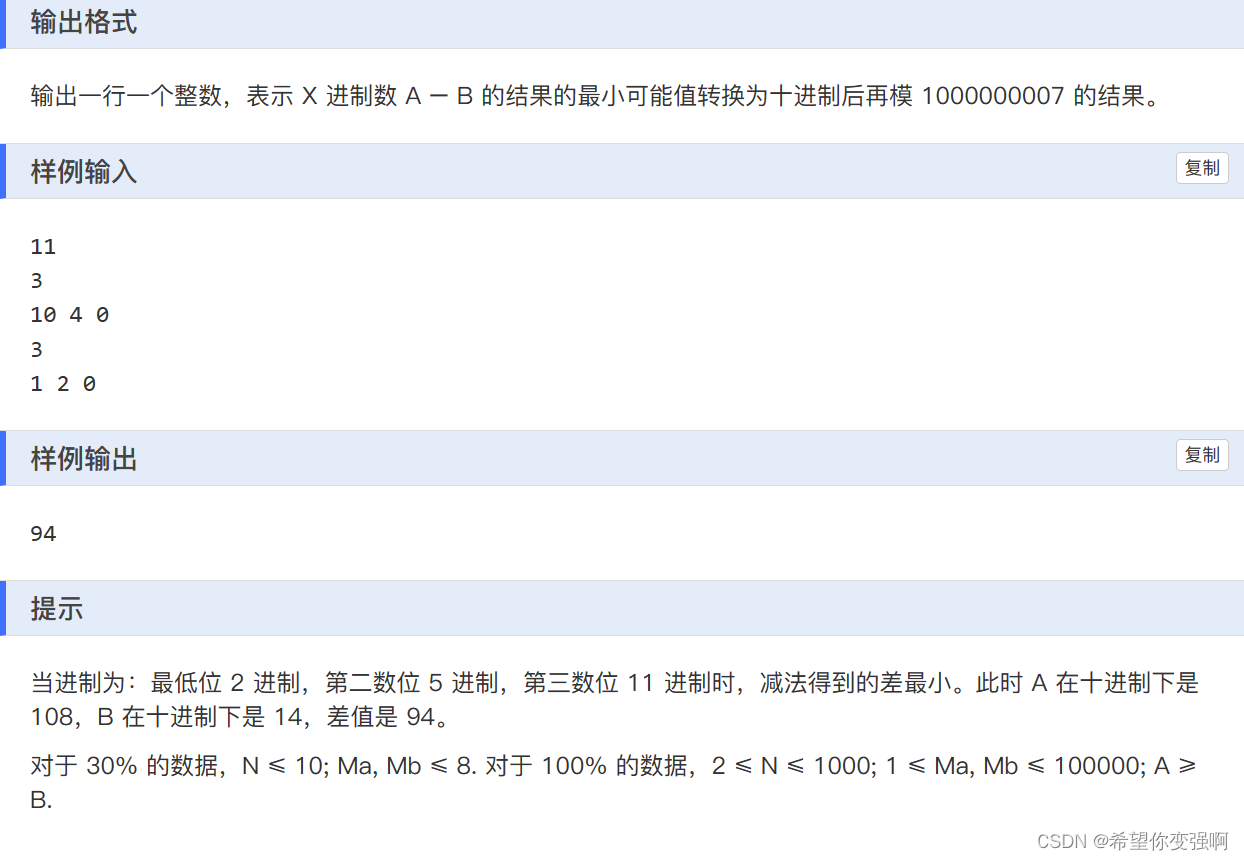
其实就是一道观察规律的题。你发现如果a这个位置上的数x,b这个位置上的数是y,那么此位置至少是max(x,y)+1进制。一定要把位置找对啊
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10,mod=1000000007;
int len1,len2;
ll tmp,ans,a[N],b[N],c[N],n;
int main(){cin>>n;cin>>len1;for(int i=len1;i>=1;i--)cin>>a[i];cin>>len2;for(int i=len2;i>=1;i--)cin>>b[i];for(int i=len1;i>=1;i--){c[i]=max(max(a[i]+1,b[i]+1),2*1ll);a[i]=a[i]-b[i];}tmp=1;for(int i=1;i<=len1;i++){ans=(tmp*a[i]+ans)%mod;tmp=(tmp*c[i])%mod;}cout<<ans;return 0;
}
/*错解
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10,mod=1000000007;
int len1,len2;
ll tmp,ans,a[N],b[N],c[N],n;
int main(){cin>>n;cin>>len1;for(int i=1;i<=len1;i++)cin>>a[i];cin>>len2;for(int i=1;i<=len2;i++)cin>>b[i];for(int i=1;i<=len1;i++){c[i]=max(max(a[i]+1,b[i]+1),2*1ll);a[i]=a[i]-b[i];//这个bug我找了两个小时,不能从高位开始减,}tmp=1;for(int i=len1;i>=1;i--){ans=(tmp*a[i]+ans)%mod;tmp=(tmp*c[i])%mod;}
cout<<ans;return 0;
}*/
数组切分
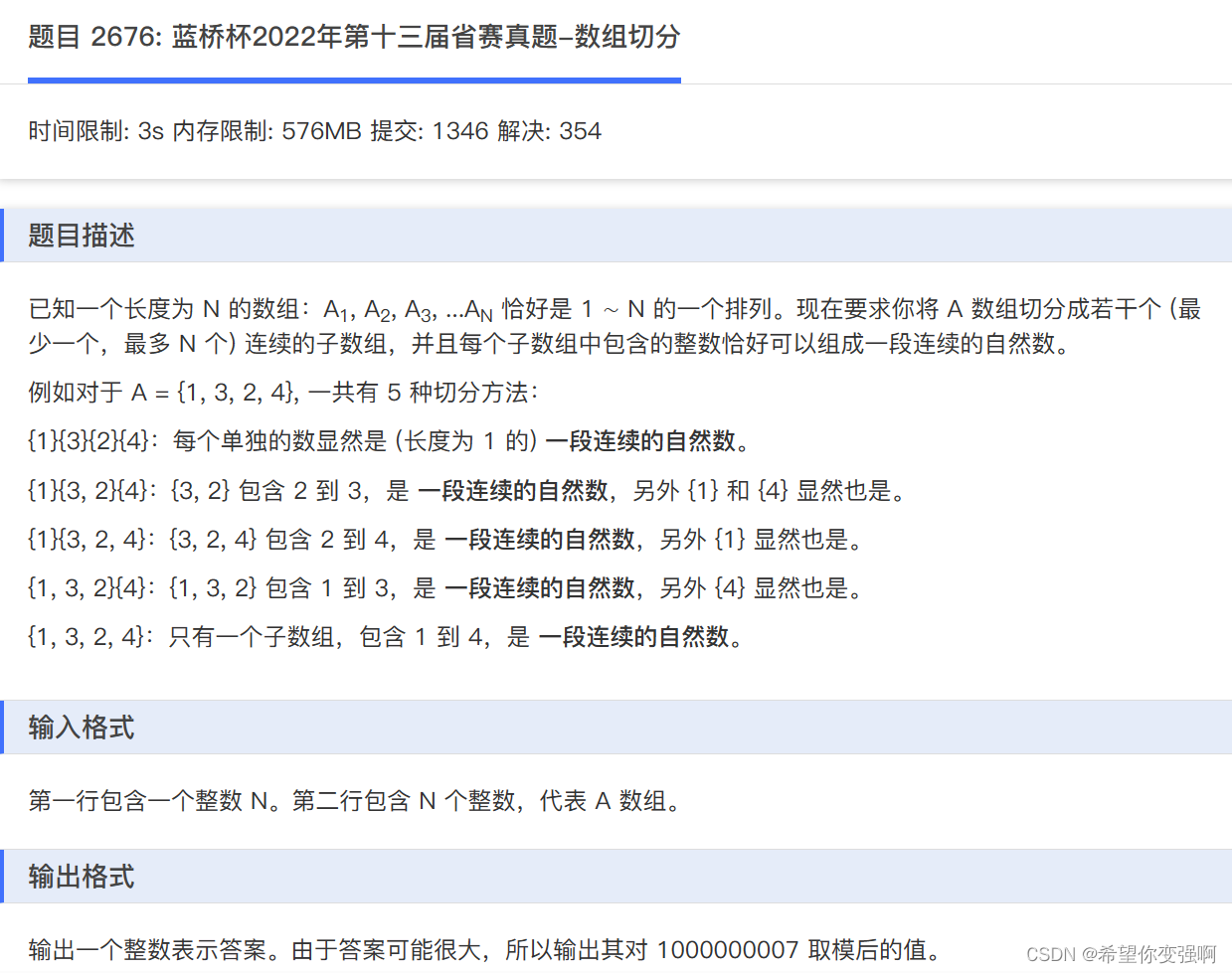
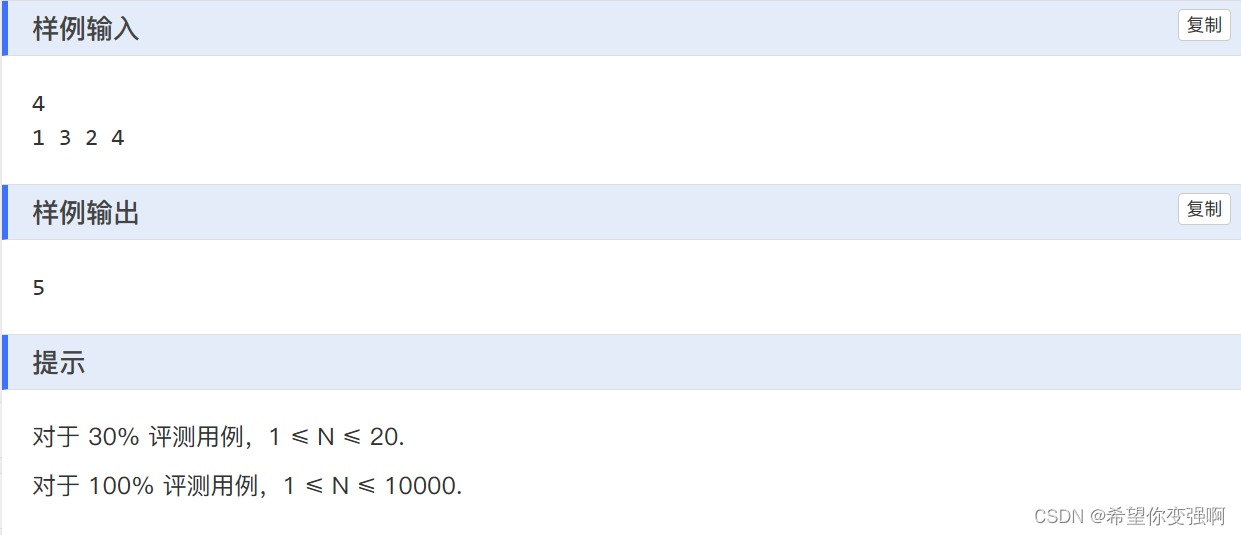
一道动态规划题,
我们设置f[i]表示从1到i区间的切法。那么可以从任意区间[j,i]转移,只要这个区间[j,i]也是满足题意的就行。那么如果判断[j,i]是否满足题意呢?
首先要注意到题上给出的是连续的的1~n的某个排列,然后我们只需要判断区间的极值和区间长度是否一样就行,如果相等,就说明此区间一定是连续的自然数。
#include <bits/stdc++.h>
using namespace std;
long long f[10010],mod =1000000007;
int a[10010],n;
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];f[0]=1;for(int i=1;i<=n;i++){int ma=a[i],mi=a[i];for(int j=i;j>=1;j--){ma=max(ma,a[j]);mi=min(mi,a[j]);if(i-j==ma-mi){f[i]=(f[i]+f[j-1])%mod;}}}cout<<f[n];return 0;
}
gcd
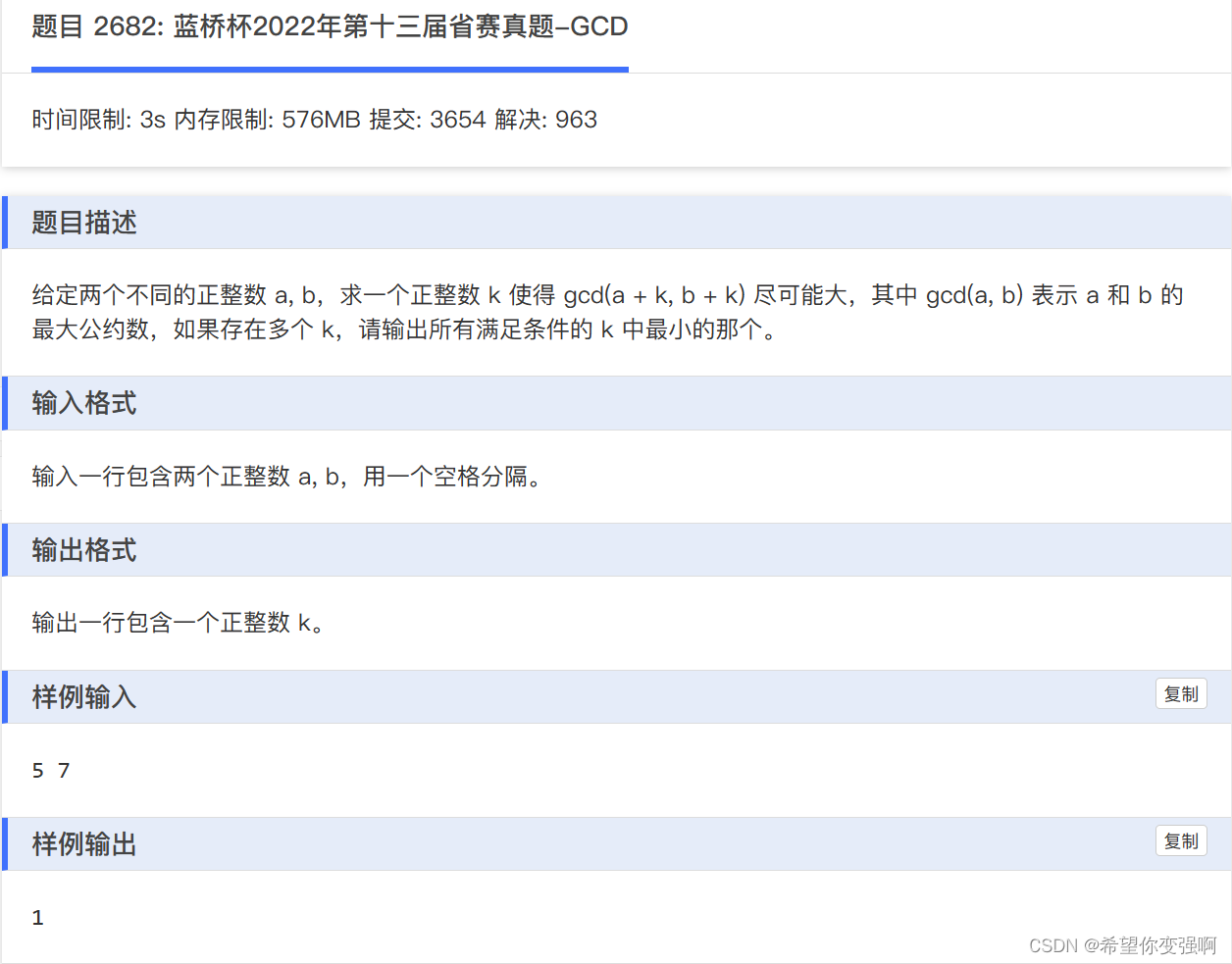

这道题本以为很麻烦,但是做着做着就发现了个不可思议的规律。
观察5和7,它们的最大gcd一定是2,为什么呢?因为你5+k和7+k始终保持差2,所以它们不可能有比2更大的gcd(因为它们两个一定是不等的)
对于一组a和b(假设b大于a),不妨另c=b-a。最终的a+k和b+k一定是差c,而且c必是它们的公因数。所以如果b+k是m*c的话,那么此时a+k必然也是c的倍数(因为它们两个差c啊),所以只需要枚举到b的下一个c的倍数即可,也就是(b/c+1)*c
验证5和9,它们差值为4,我们枚举到8和12时候发现gcd已经是4了,那么k就确定了
验证2和9,它们差值为7,我们一直枚举到7和14时发现gcd为7,那么此时k也确定了
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,b,s,c;
int main(){cin>>a>>b;c=abs(a-b);if(a>b)swap(a,b);s=b/c;cout<<(s+1)*c-b;return 0;
}
青蛙过河
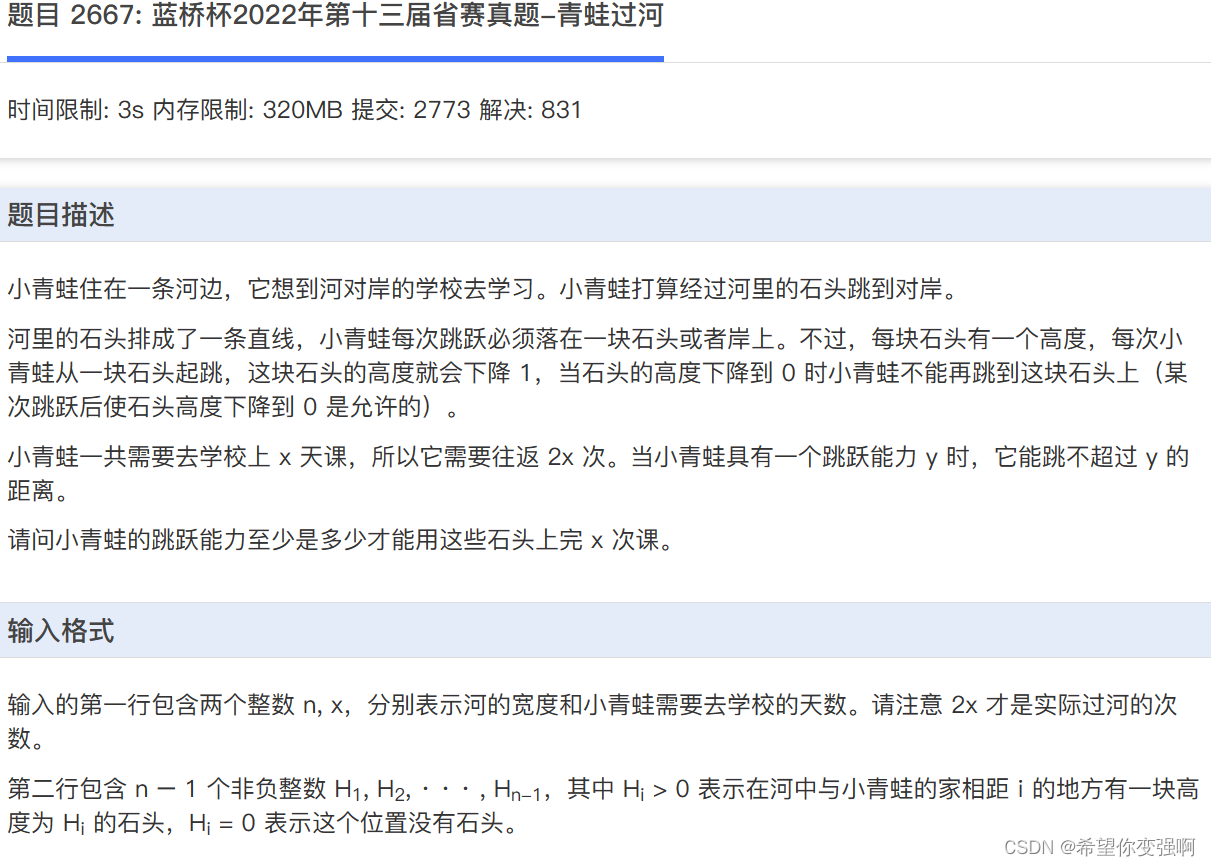

二分做法:
我们对跳跃距离二分,然后去判断这个距离能不能跑2x次即可,既然我们都已经确定了区间长度了。
那么不妨我们把这整个长度分成等长的mid区间,只需要保证所有的mid长度区间和都是大于2x的就行。
证明:(我只会反证法)
假设存在一组mid长度的区间和小于2x,那么经过x次来回,必然要经过此区间2x次,所以不成立。故原假设成立。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long ll;
int s[N];
ll n,x;
bool check(int m){for(int i=1;i+m<=n;i++){if(s[i+m-1]-s[i-1]<2*x) return false;}return true;
}
int main(){cin>>n>>x;int a;for(int i=1;i<n;i++)cin>>a,s[i]=s[i-1]+a;int l=1,r=n;while(l<=r){int mid=(l+r)>>1;if(check(mid)) r=mid-1;else l=mid+1;}cout<<l;return 0;
}相关文章:

第十三届蓝桥杯真题:x进制减法,数组切分,gcd,青蛙过河
目录 x进制减法 数组切分 gcd 青蛙过河 x进制减法 其实就是一道观察规律的题。你发现如果a这个位置上的数x,b这个位置上的数是y,那么此位置至少是max(x,y)1进制。一定要把位置找对啊 #include <bits/stdc.h> using namespace std; typedef l…...
)
JavaEE初阶Day 6:多线程(4)
目录 Day 6:多线程(4)1. 线程不安全的原因2. 锁3. synchronized Day 6:多线程(4) 前序:针对Day 5结尾的count 多线程的执行,是随机调度抢占式的执行模式,某个线程执行指…...

微信小程序 django+nodejs电影院票务售票选座系统324kd
小程序Android端运行软件 微信开发者工具/hbuiderx uni-app框架:使用Vue.js开发跨平台应用的前端框架,编写一套代码,可编译到Android、小程序等平台。 前端:HTML5,CSS3 VUE 后端:java(springbootssm)/python(flaskdja…...
基于springboot实现桂林旅游景点导游平台管理系统【项目源码+论文说明】计算机毕业设计
基于springboot实现桂林旅游景点导游平台管理系统演示 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了桂林旅游景点导游平台的开发全过程。通过分析桂林旅游景点导游平台管理的不足,创建了一个计算…...
idea 开发serlvet汽车租赁管理系统idea开发sqlserver数据库web结构计算机java编程layUI框架开发
一、源码特点 idea开发 java servlet 汽车租赁管理系统是一套完善的web设计系统sqlserver数据库 系统采用serlvetdaobean mvc 模式开发,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 java se…...

Unity之PUN实现多人联机射击游戏的优化(Section 3)
目录 💣一、准备工作 💣二、生成弹头脚本的编写 💣三、实现发射和伤害同步 手雷都加了在给狗剩加个火箭筒不过分吧。效果看GIF动图,分别是单机和联机的效果。 添加火箭筒依旧是在原有的基础上更改,我查看火箭筒模型…...
PDF锐化
PDF Shaper Ultimate(pdf转图片) 编辑->添加文件->选中一个要处理的pdf 操作->转换->PDF转为图片 ComicEnhancerPro设置(把图片锐化) PDF Shaper Ultimate(图片转pdf) 编辑-添加图片->选中所有锐化处理后的图片 转换->图片转为pdf(会把所有图…...

【python和java】
如何理解java和python的不同,在java中,先有类,类生出对象,对象承载数据。而python是直接数据,没有类的概念 理解 Java 和 Python 在面向对象编程(OOP)方面的不同,关键在于理解它们各…...
C盘满了怎么办,清理工具TreeSize
TreeSize是一款强大的磁盘空间分析工具,它可以帮助用户轻松地找出电脑中占用空间最多的文件和程序,从而让用户进行针对性地删除或卸载。 占用空间很小 下载链接:https://pan.quark.cn/s/bea23ed6b1d3...

【vue】watch 侦听器
watch:可监听值的变化,旧值和新值 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><titl…...
校招生如何准备软件测试、测试开发岗位的面试?
校招生如何准备软件测试、测试开发岗位的面试? 求职建议 大家都很困惑如何学习测试?如何准备测试方面的面试? 我有朋友是做研发的,他认为测试不用准备,直接用开发的简历就行。也有人认为要学习一些测试理论…...

蓝桥杯抱佛脚篇~
文章目录 基础语法输入输出集合(set)排序 基础语法 输入输出 # 输入一个数 nint(input())# 输入两、三个数,例如:1 2 或者 1 2 3 x,y map(int,input().split())# 输入数组 # ——— 1 —— nums[int(i) for i in input().split()] print(n…...

基于springboot的大学城水电管理系统源码数据库
基于springboot的大学城水电管理系统源码数据库 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了大学城水电管理系统的开发全过程。通过分析大学城水电管理系统管理的不足,创建了一个计算机管理大学城水…...
AI大模型探索之路-应用篇2:Langchain框架ModelIO模块—数据交互的秘密武器
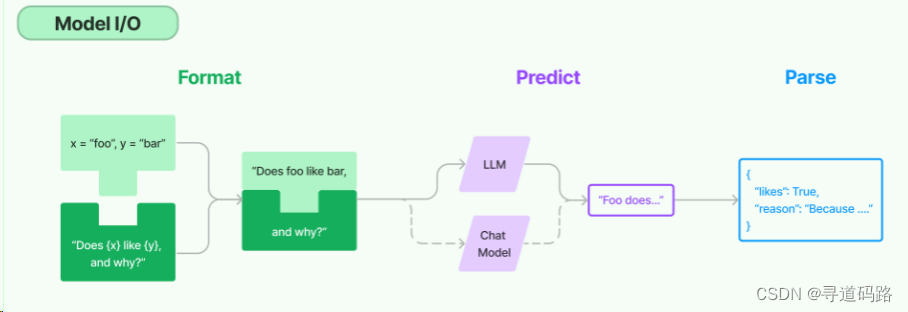
目录 前言 一、概述 二、Model 三、Prompt 五、Output Parsers 总结 前言 随着人工智能技术的不断进步,大模型的应用场景越来越广泛。LangChain框架作为一个创新的解决方案,专为处理大型语言模型的输入输出而设计。其中,Model IO&#…...

【SSH】群晖开启ssh访问
群晖开启ssh访问 假设 你需要设置群晖 账号 test-user 开启ssh访问 设置 你的 test-user 为管理员权限 否则你无法通过cmd 面板 连接访问 群晖你需要哪个账号 就使用哪个账号终端 cmd连接 否则需要考虑后续创建 rsa 公密钥文件的 所属权 问题账号密码连接登录终端 ssh -p 端…...

Vue 移动端(H5)项目怎么实现页面缓存(即列表页面进入详情返回后列表页面缓存且还原页面滚动条位置)keep-alive缓存及清除keep-alive缓存
一、需求 产品要求:Vue移动端项目进入列表页,列表页需要刷新,而从详情页返回列表页,列表页则需要缓存并且还原页面滚动条位置 二、实现思路 1、使用Vue中的keep-alive组件,keep-alive提供了路由缓存功能 2、因为我项…...
【MVCC】深入浅出彻底理解MVCC
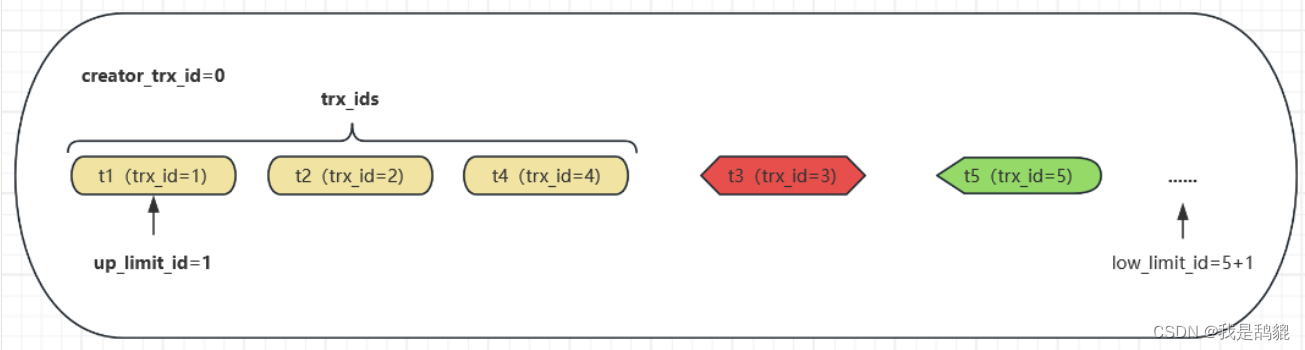
MVCC概述 MVCC(Multi-Version Concurrency Control)即多版本并发控制。主要是为了提高数据库的并发性能而提供的,采用了不加锁的方式处理读-写并发冲突,确保了任何时刻的读操作都是非阻塞的。只需要很小的开销,就可以…...
【问题解决】ubuntu安装新版vscode报code-insiders相关错误
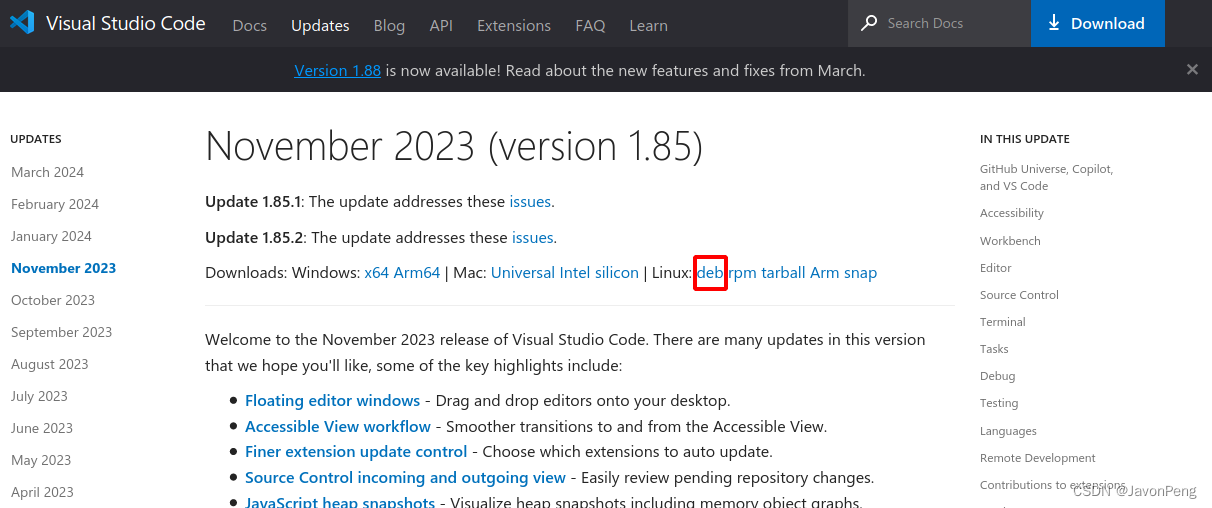
问题 目前 vscode官网 最新的包为 insiders_1.89.0-1712297812_amd64.deb ,双击或者使用sudo dpkg -i code-insiders_1.89.0-1712297812_amd64.deb安装后报错,执行其他命令也报错。 安装环境:ubuntu18.04 dpkg: 处理软件包 code-insiders (…...

【Python】面向对象(专版提升2)
面向对象 1. 概述1.1面向过程1.2 面向对象 2. 类和对象2.1 语法2.1.1 定义类2.1.2 实例化对象 2.2 实例成员2.2.1 实例变量2.2.2 实例方法2.2.3 跨类调用 3. 三大特征3.1 封装3.1.1 数据角度3.1.2 行为角度3.1.3 案例:信息管理系统3.1.3.1 需求3.1.3.2 分析3.1.3.3 设计 3.2 继…...
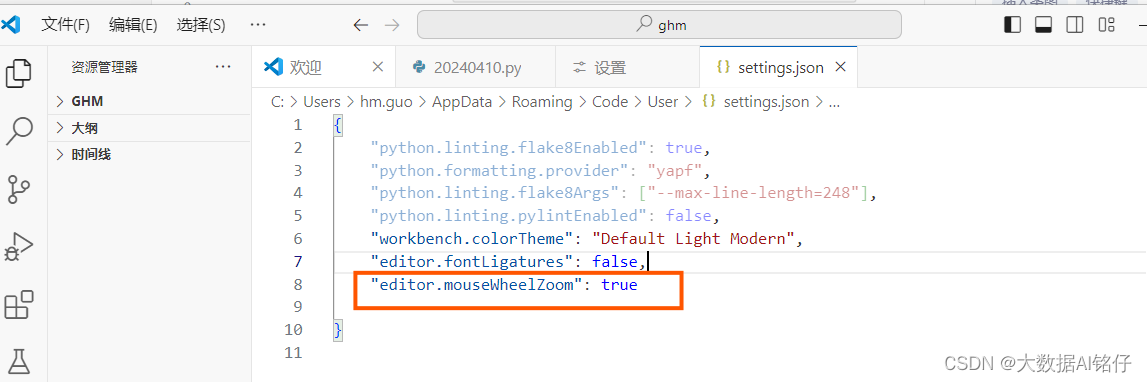
Vscode设置滚轮进行字体大小的调节
Vscode设置滚轮进行字体大小的调节 正常的话按 ctrl 或者 ctrl - 进行字体的大小调节 1.打开Vscode,找打设置的图标,在点击设置,或者直接使用快捷键,【ctrl ,】 2. 在搜索框搜索Font Ligatures 3.双击进入settings.json ,找到如…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
