算法设计与分析实验报告c++实现(N皇后问题、卫兵布置问题、求解填字游戏问题、图的m着色问题)
一.N皇后问题
基本原理和思路:
从一条路往前走,能进则进,不能进则退回来,换一条路再试。在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。
而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
代码实现如下:
#include <iostream>
#include <cmath>
using namespace std;
//皇后的个数,方案数目
int n,sum=0;
//记录放置方案
int x[100];//不能这样定义int *x;
//用户递归求取方案
void Queen1(void);
void TraceBack(int);
void PrintMethod(void);
//检查这一皇后放置方案是否满足要求
int Place(int);int main()
{cout << "输入皇后个数:" << endl;cin>>n;Queen1();return 0;
}void Queen1(void)
{TraceBack(0);
}
void TraceBack(int r)
{int i;if(r>=n){PrintMethod();//这个函数的正确性还没有得到验证sum++;}else{for(i=0;i<n;i++){x[r]=i;//在下一行判断当前路是不可行的之后,进入同级的另外的路径if(Place(r))//先试探当前这条路是可行的,则进入下一步循环TraceBack(r+1);}}
}
void PrintMethod(void)
{int i,j;cout<<"第"<<sum<<"个方案\n";for(i=0;i<n;i++){for(j=0;j<n;j++){if(j==x[i])cout<<"1";elsecout<<"0";}cout<<endl;}
}
int Place(int r)
{int i;for(i=0;i<r;i++){if(x[r]==x[i] || abs(r-i)==abs(x[r]-x[i]))//在此处判断皇后走的下一步路是否可行,如果不可行性,return 0;return 0;}return 1;
}分析:时间复杂度为O(n^n)
二.卫兵步列问题
基本原理和思路:初始令所有的 X [i, j]= 1, i =1,2, …… m , j =1,2, ……n . 算法从 (1,1 )开始直到 (m,n)为止, 搜索树是二叉树,有 m x n 层 . 每个结点对应一个陈列室位置,如果令 X [i, j]= 0 ,取消(i,j ) 位置的哨兵,进入左子树;否则进入右子树。在进入左子树时需要检查房间被监视的情况。 即当取消( i,j )位置的哨兵时,此位置及其上、下、左、右位置是否被监视。
代码实现如下:
#include<iostream>
#include<fstream>
#include<queue>using namespace std;
class Solve;class Node //Node节点,用来存放搜索树的节点
{friend class Solve;
private:int i; //当前要放置的新位置 横坐标:i 纵坐标:jint j;int robotNums; //当前节点已经放置的哨兵数目int beenMonitored; //当前已经被监视的房间数int** x; //当前放置哨兵的地方 0表示没有,1表示放置了int** y; //当前已经被监视的地方 0表示没有,1表示已经监视了int m; //行int n; //列public:Node(); //构造函数Node(int m, int n); //构造函数,m、n是行列数Node(const Node& a); //这个函数是用于heap的push,push会调用复制构造函数,因此必须自定义一个friend bool operator<(const Node& a, const Node& b); //重载<,用于优先队列的使用Node& operator=(const Node& a) //赋值运算符,懒得换位置了{if (x || y){for (int i = 0; i < m + 2; ++i){if (x){delete[] x[i];}if (y){delete[] y[i];}}delete[] x;delete[] y;x = NULL;y = NULL;}i = a.i;j = a.j;robotNums = a.robotNums;beenMonitored = a.beenMonitored;m = a.m;n = a.n;x = new int* [m + 2];y = new int* [m + 2];for (int i = 0; i < m + 2; ++i){x[i] = new int[n + 2];y[i] = new int[n + 2];for (int j = 0; j < n + 2; ++j){x[i][j] = a.x[i][j];y[i][j] = a.y[i][j];}}return *this;}~Node(); //用到了new,因此析构函数要重载,避免内存泄露};class Solve //解决问题的类
{
private:priority_queue<Node> heap; //优先队列heapint ans; //答案所需要的哨兵数目int m; //行列数int n;int** result; //答案哨兵的排列顺序public:Solve();Solve(int m, int n);void run(ofstream& fcout); //进行整个计算+输出void get_min(); //运用分支限界法,寻找最小值void print(ofstream& fcout); //打印哨兵位置和数目void copy(int** x, int** y); //将一个二维数组赋值给另一个void change(Node& tmp, int i, int j); //生成子节点,同时将其添加到heap中
};int main()
{ifstream fcin;fcin.open("input.txt");if (!fcin.is_open()){cout << "文件 input.txt 未能打开" << endl;return -1;}int m, n;fcin >> m >> n;fcin.close();Solve solve(m, n);ofstream fcout;fcout.open("output.txt");if (!fcout.is_open()){cout << "文件 output.txt 未能打开" << endl;return -1;}solve.run(fcout);fcout.close();return 0;
}分析:复杂度 W(n,m)=O(nm2)。
三. 求解填字游戏问题
- 基本原理和思路:从(0,0)开始向右搜索,搜到(3,0)结束
- 搜索时记录那些点被用过,下一个点一定是没有被用过的点,使用vis数组标记
- 退出条件:搜索到 x == 3时,即此时九个点都已经填了一遍值,输出填入的九个值
- 改点是否可以填入,是否合法:使用check函数来检查一下,由于是从左向右开始填起,所以相邻元素只需要考虑上和下两个方向,check函数加上判断边界的条件即可。
- 若该点合法,则填入该点,否则继续循环找一个可选点。
- 判断边界:即不能超出 3 * 3 的范围,到了最右边要进行换行,否则横坐标直接++即可!具体实现:if(y == 2) dfs(x + 1, 0); else dfs(x, y + 1);
- 最后取消标记,回溯上一个点,找下一种选择情况。
代码实现如下:
#include <iostream>using namespace std;int a[3][3], count;
bool vis[10];bool isprime(int n)
{for(int i = 2; i * i <= n; i++){if(n % i == 0) return false;}return true;
}bool check(int x, int y, int k)
{// 上 if(x - 1 >= 0 && !isprime(a[x - 1][y] + k)) return false;// 左 if(y - 1 >= 0 && !isprime(a[x][y - 1] + k)) return false;return true;
}void dfs(int x, int y)
{if(x == 3){for(int i = 0; i < 3; i++){for(int j = 0; j < 3; j++){cout << a[i][j] << " ";}cout << endl;}cout << endl;count ++;return;}for(int i = 1; i <= 10; i++){if(!vis[i] && check(x, y, i)){a[x][y] = i; vis[i] = true;if(y == 2) dfs(x + 1, 0);else dfs(x, y + 1);a[x][y] = 0; vis[i] = false;}}
}int main()
{dfs(0, 0);cout << "Total: " << count << endl;return 0;
}分析:采用回溯法,即求全排列,时间复杂度O(n!)
四.求解图的m着色问题
基本原理和思路:MaxSum(i,j):从第i行j列到底边的最大数字之和
从最后一行开始递推,MaxSum(n,j)=D(n,j)//n行j列,MaxSum(n-1,j) = D(n-1,j) + max( MaxSum(n,j) , MaxSum(n,j+1) )
然后为了减少空间,不需要用二维数组来存储MaxSum(n,j)的值,只需要求MaxSum(n,j)的时候存储下一行MaxSum(n+1,j)的值就可以,然后计算完第n行的MaxSum之后再覆盖原来的第n+1行的MaxSum的值。
代码实现如下:
#include <iostream>
#include <cmath>
#include <cstdio>
#include <algorithm>using namespace std;const int N = 5;//图的顶点数
const int M = 3;//色彩数
class Color
{friend int mColoring(int, int, int **);
private:bool Ok(int k);void Backtrack(int t);int n, //图的顶点数m, //可用的颜色数**a, //图的邻接矩阵*x; //当前解long sum; //当前已找到的可m着色方案数
};
int mColoring(int n,int m,int **a);
int main()
{int **a = new int *[N+1];for(int i=1; i<=N; i++){a[i] = new int[N+1];}cout<<"请输入图G的邻接矩阵:"<<endl;for(int i=1; i<=N; i++){for(int j=1; j<=N; j++){cin>>a[i][j];}cout<<endl;}cout<<"图G的着色方案如下:"<<endl;cout<<"当m="<<M<<"时,图G的可行着色方案数目为:"<<mColoring(N,M,a)<<endl;for(int i=1; i<=N; i++){delete[] a[i];}delete []a;
}void Color::Backtrack(int t)
{if (t>n){sum++;for (int i=1; i<=n; i++)cout << x[i] << " ";cout << endl;}else{for (int i=1; i<=m; i++){x[t]=i;if (Ok(t)) Backtrack(t+1);x[t]=0;}}
}bool Color::Ok(int k)// 检查颜色可用性
{for (int j=1; j<=n; j++){if ((a[k][j]==1)&&(x[j]==x[k])) //相邻且颜色相同{return false;}}return true;
}int mColoring(int n,int m,int **a)
{Color X;//初始化XX.n = n;X.m = m;X.a = a;X.sum = 0;int *p = new int[n+1];for(int i=0; i<=n; i++){p[i] = 0;}X.x = p;X.Backtrack(1);delete []p;return X.sum;
}分析:时间复杂度是 O ( m ∗ n 2 ) O(m*n^2) O(m∗n2)。
相关文章:
)
算法设计与分析实验报告c++实现(N皇后问题、卫兵布置问题、求解填字游戏问题、图的m着色问题)
一.N皇后问题 基本原理和思路: 从一条路往前走,能进则进,不能进则退回来,换一条路再试。在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一…...

深入探索Linux中的libgdbus:GDBus库的应用和实现
引言 在Linux系统中,DBus是一种高效的进程间通信(IPC)机制,广泛应用于桌面环境和系统服务之间的通信。GDBus是基于GLib库的DBus实现,作为libgdbus的一部分提供。它旨在提供一种简洁、高效的方式来实现DBus通信。通过深…...

MacOS下Qt 5开发环境安装与配置
最近笔者在MacOS中使用Qt Creator开发Qt程序时遇到了一些问题,在网上查了不少资料,都没有找到解决方案,只有自己进行研究摸索了,今天晚上终于将目前遇到的问题全部解决了,特记录下来分享给大家。 笔者使用的是MacOS 1…...

jquery 实现倒计时
$(".tableText").click(function () { var time 60; var timer setInterval(function(){ time--; $(".tableText").text("("time"秒)重发"); if(time0){ clearI…...

MYSQL 5.7重置root密码
Mysql 5.7重置root密码 如果您忘记了MySQL 5.7的root密码,可以通过以下步骤重置: 停止MySQL服务。在命令行中输入以下命令: systemctl stop mysqld启动MySQL服务并跳过授权表。在命令行中输入以下命令: mysqld_safe --skip-gra…...

博客永久链接与计数
概述 工欲善其事,必先利其器。 对自己的博客不好用不满意很久了,但是这几年太懒。想趁着放假弄一下吧,发现几年没动,版本升级后很多东西变了,折腾了一下午效果不太理想。先记录一下。 问题 博客链接中有中文&#x…...

基于 RisingWave 和 ScyllaDB 构建事件驱动应用
概览 在构建事件驱动应用时,人们面临着两大挑战:1)低延迟处理大量数据;2)实现流数据的实时摄取和转换。 结合 RisingWave 的流处理功能和 ScyllaDB 的高性能 NoSQL 数据库,可为构建事件驱动应用和数据管道…...

mysql8.0高可用集群架构实战
MySQL :: MySQL Shell 8.0 :: 7 MySQL InnoDB Cluster 基本概述 InnoDB Cluster是MySQL官方实现高可用读写分离的架构方案,其中包含以下组件 MySQL Group Replication,简称MGR,是MySQL的主从同步高可用方案,包括数据同步及角色选举Mysql Shell 是InnoDB Cluster的管理工具,用…...
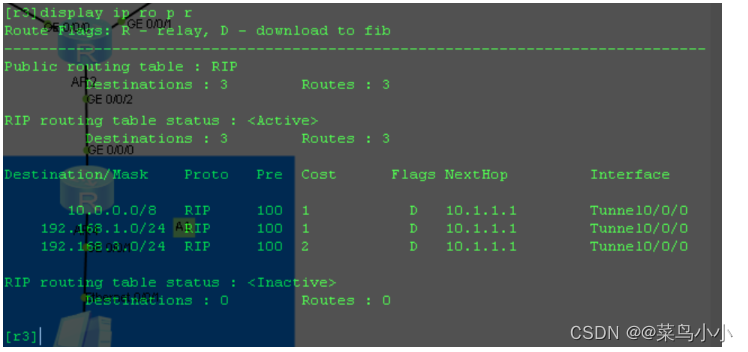
GRE/MGRE详解
GRE GRE:通用路由封装,是标准的三层隧道技术,是一种点对点的隧道技术; 该技术可以实现不同的网络之间安全的访问; 如上:可以使用该技术搭建一条专线,实现公司A与分公司A1之间相互通信…...
蓝桥杯(填空题)
十四届 B组 日期统计(暴力枚举) 数据 5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2 7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1 0 0 9 4 8 0 9 1 2 8 5 0 2 5 3…...

vim快捷指令
Vim是一款强大的文本编辑器,它提供了许多快捷指令来提高编辑效率。以下是一些常用的Vim快捷指令: 移动光标: h 向左移动一个字符j 向下移动一行k 向上移动一行l 向右移动一个字符w 跳到下一个单词的开头b 跳到前一个单词的开头e 跳到当前单词…...

LINUX 下IPTABLES配置详解
-t<表>:指定要操纵的表; -A:向规则链中添加条目; -D:从规则链中删除条目; -i:向规则链中插入条目; -R:替换规则链中的条目; -L:显示规则链中…...

CentOS 网卡ifcfg-eth0 ping不通外网(www.baidu.com)
1、如果确认好就直接激活网卡! ifup eth0 2、慢慢找: cd /etc/sysconfig/network-scripts/ ls 找到你的网卡是啥,这里网卡是 ifcfg-eth0 执行1就好了!...
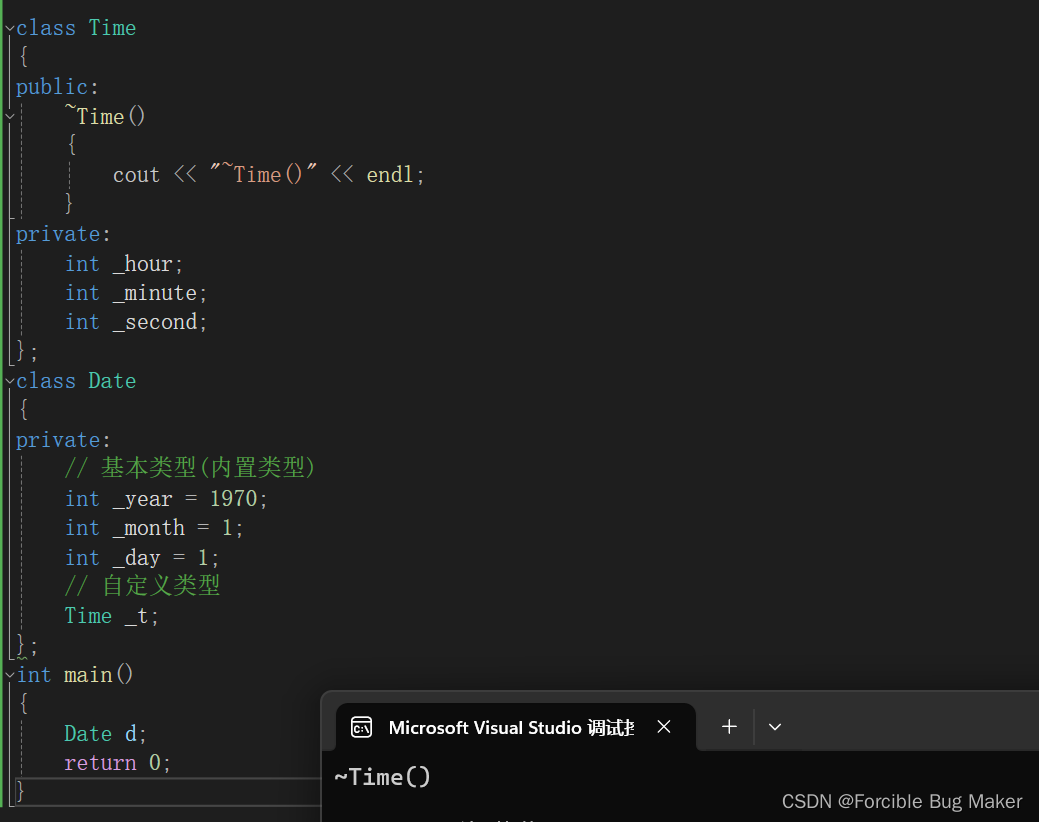
【C++】类和对象②(类的默认成员函数:构造函数 | 析构函数)
🔥个人主页:Forcible Bug Maker 🔥专栏:C 目录 前言 类的6个默认成员函数 构造函数 概念 构造函数的特性及用法 析构函数 概念 析构函数的特性及用法 结语 前言 本篇主要内容:类的6个默认成员函数中的构造函…...
)
【ZZULIOJ】1063: 最大公约与最小公倍(Java)
目录 题目描述 输入 输出 样例输入 Copy 样例输出 Copy 提示 code 题目描述 输入两个正整数,输出其最大公约数和最小公倍数。 输入 输入两个正整数n和m(n,m<1000000)。输入保证最终结果在int范围内。 输出 输出两个整数,用空格…...

遍历列举俄罗斯方块的所有形状
以前玩俄罗斯方块的时候,就想过一个问题,为什么俄罗斯方块就这7种形状,还有没有别的形状?自己也在纸上画过,比划来比划去,确实就这几种形状。 继续思考一下,那假如是3个块组合的形状࿰…...
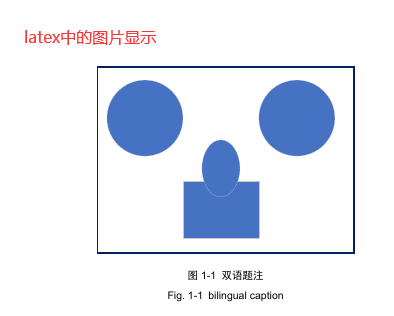
将Visio绘图导出PDF文件,使其自适应大小,并去掉导入Latex的边框显示
问题描述 将Visio绘图导成pdf文件,首先在Visio绘图如下: 如果直接导出或者另存为pdf文件,则会发现pdf文件是整个页面大小,而不是图片大小。而且在导入latex等排版工具现实时,会显示边框。 问题解决 1.调整Visio中的页…...
android支付宝接入流程
接入前准备 接入APP支付能力前,开发者需要完成以下前置步骤。 本文档展示了如何从零开始,使用支付宝开放平台服务端 SDK 快速接入App支付产品,完成与支付宝对接的部分。 第一步:创建应用并获取APPID 要在您的应用中接入支付宝…...

Mac 下 Python+Selenium 自动上传西瓜视频
背景 研究下 PythonSelenium 自动化测试框架,简单实现 Mac 下自动化批量上传视频西瓜视频并发布,分享给需要的同学(未做过多的异常处理)。 脚本实现 首先通过手工手机号登录,保存西瓜视频网站的 cookie 文件 之后加载…...
六:ReentrantLock —— 可重入锁
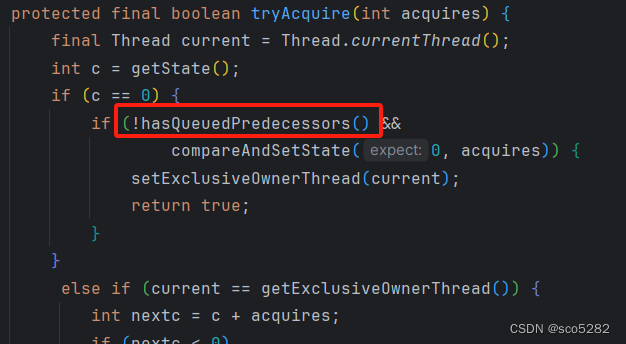
目录 1、ReentrantLock 入门2、ReentrantLock 源码解析2.1、构造方法:默认为非公平锁2.2、三大内部类2.2、lock():加锁【不可中断锁】2.2.1、acquire() 方法 —— AQS【模板方法】2.2.2.1 tryAcquire() 方法 —— AQS,由子类去实现2.2.2.2. a…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
