力扣刷题 二叉树层序遍历相关题目II
NO.116 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:

输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = [] 输出:[]
本题难点在于如何填充每个节点的next 指针,让这个指针指向其下一个右侧节点。如何获取队列中下一个节点,我们还没有遍历到下一个节点,怎么能获取下一个节点的指针呢?
这里的思路是保存上一个遍历节点的指针,让它的next指针指向当前节点。是不是很巧妙,和我们自然的思路不太一样。
因为我们用到了前节点的变量,而头节点并没有前节点,所以需要单独考虑情况。
完整代码如下
class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();//建立当前节点Node* node;Node* prenode;// 遍历队列,放入数组for(int i = 0; i < size; i++ ){//如果遍历到这一层的头节点if(i == 0){node = que.front();prenode = node;}else{//出队列第一个元素放入数组node = que.front();//上一个节点的next指针指向当前节点prenode->next = node;//将前节点更新为当前节点prenode = node;}//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();}//这一层遍历完,将最后一个元素的next设置为nullnode->next = NULL;}return root;}
};总结与反思
层序遍历最关键的是深刻理解整个for循环是每一层遍历的核心,这样添加代码就会更加自如,知道是在层前还是层中还是层后。
写完代码,可以验证一遍测试用例,发现bug,避免显而易见的错误。
NO.117 填充每个节点的下一个右侧节点指针II
给定一个二叉树:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例 1:
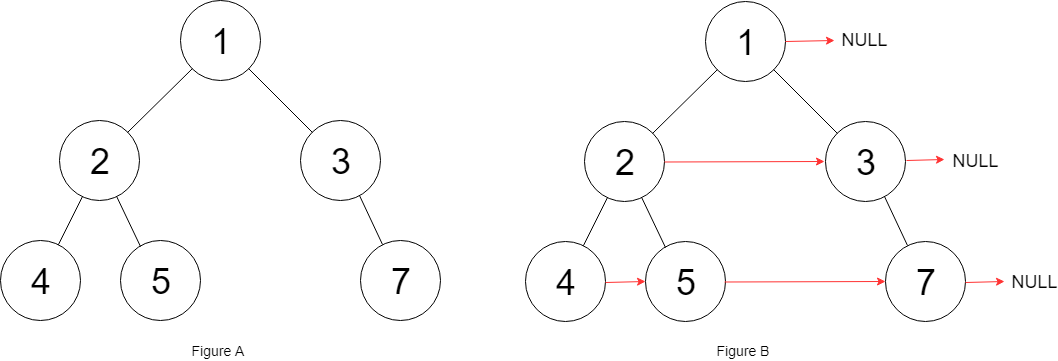
输入:root = [1,2,3,4,5,null,7] 输出:[1,#,2,3,#,4,5,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
示例 2:
输入:root = [] 输出:[]
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
完整代码如下
class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();//建立当前节点Node* node;Node* prenode;// 遍历队列,放入数组for(int i = 0; i < size; i++ ){//如果遍历到这一层的头节点if(i == 0){node = que.front();prenode = node;}else{//出队列第一个元素放入数组node = que.front();//上一个节点的next指针指向当前节点prenode->next = node;//将前节点更新为当前节点prenode = node;}//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();}//这一层遍历完,将最后一个元素的next设置为nullnode->next = NULL;}return root;}
};NO.104 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
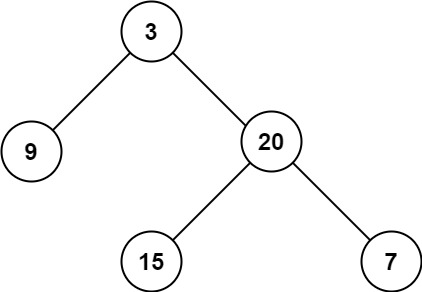
输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
完整代码如下
class Solution {
public:int maxDepth(TreeNode* root) {queue<TreeNode*> que;//记录最大深度int depth = 0;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();// 遍历队列,放入数组for(int i = 0; i < size; i++ ){TreeNode* node = que.front();//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();} depth++;}//循环结束说明遍历完最后一层,返回深度return depth;}
};NO.111 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
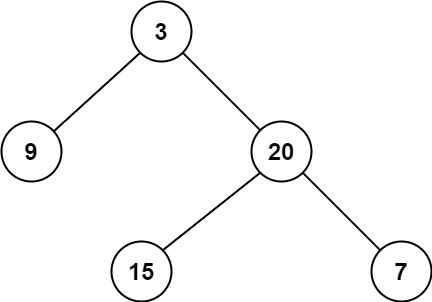
输入:root = [3,9,20,null,null,15,7] 输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
完整代码如下
class Solution {
public:int minDepth(TreeNode* root) {queue<TreeNode*> que;//记录深度int depth = 0;if(root != NULL){que.push(root);}while(!que.empty()){// 如何判断每一层的个数//记录队列的大小int size = que.size();// 遍历队列,放入数组depth++;for(int i = 0; i < size; i++ ){TreeNode* node = que.front();//一旦找到叶子节点就返回深度if(node->left == NULL && node->right == NULL) return depth;//将左右节点入队列if(node->left) que.push(node->left);if(node->right) que.push(node->right);//将当前节点弹出que.pop();} }return 0;}
};相关文章:

力扣刷题 二叉树层序遍历相关题目II
NO.116 填充每个节点的下一个右侧节点指针 给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下: struct Node {int val;Node *left;Node *right;Node *next; } 填充它的每个 next 指针,…...

智能电网将科技拓展至工厂之外的领域
【摘要/前言】 物联网已然颠覆我们日常生活的许多层面。在家居方面,家电变成连网设备,不仅让我们能控制灯光与上网购物,甚至在出门时提供安全功能。在工业领域,智能工厂改变产品制造的方式。工业物联网(IIoT)不仅让制造商更加敏捷…...

单列模式1.0
单列模式 单例模式能保证某个类在程序中只存在唯⼀⼀份实例, ⽽不会创建出多个实例 1.饿汉模式 只要程序一启动就会立即创建出一个对象 class Signleton{private static Signleton instancenew Signleton();//防止在以后的代码中再创建对象,我们将构造方法private,…...

golang kafka sarama源码分析
一些理论 1.topic支持多分区,每个分区只能被组内的一个消费者消费,一个消费者可能消费多个分区的数据; 2.消费者组重平衡的分区策略,是由消费者自己决定的,具体是从消费者组中选一个作为leader进行分区方案分配&#…...
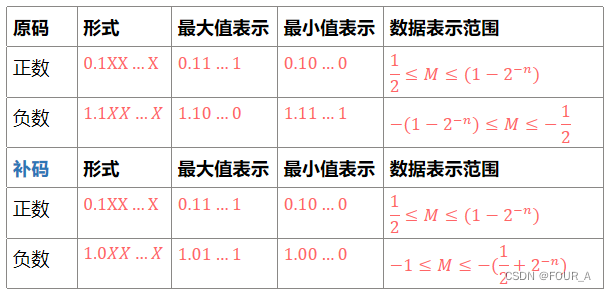
计算机组成原理【CO】Ch2 数据的表示和应用
文章目录 大纲2.1 数制与编码2.2 运算方法和运算电路2.3 浮点数的表示和运算 【※】带标志加法器OFSFZFCF计算机怎么区分有符号数无符号数? 【※】存储排列和数据类型转换数据类型大小数据类型转换 进位计数制进制转换2的次幂 各种码的基本特性无符号整数的表示和运算带符号整…...

dfs回溯 -- Leetcode46. 全排列
题目链接:46. 全排列 题目描述 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示…...
设计模式-接口隔离原则
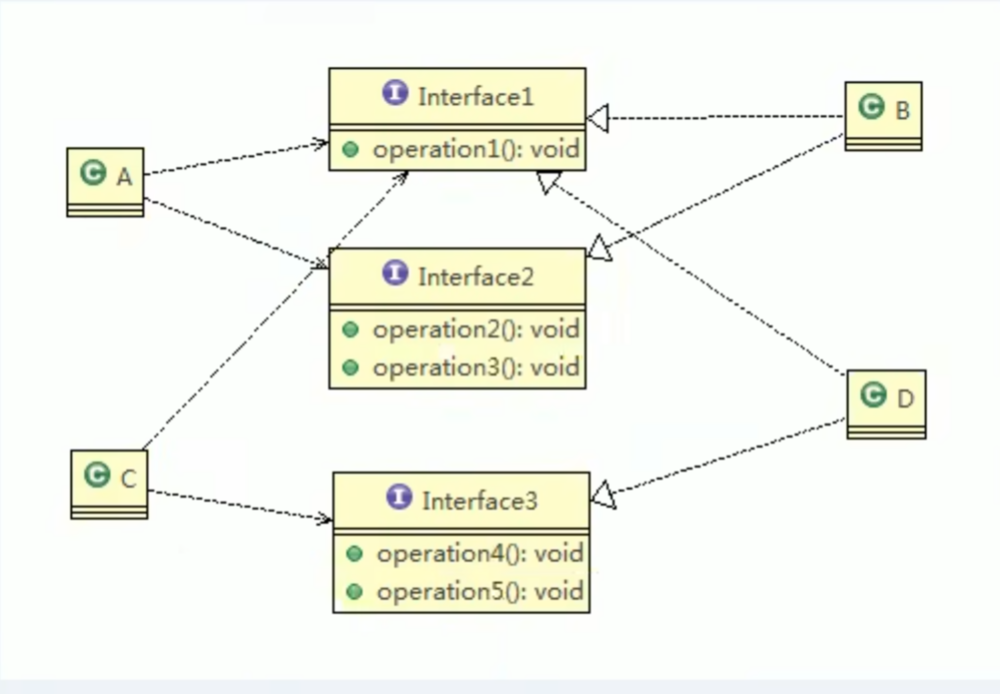
基本介绍 客户端不应该依赖它不需要的接口,即一个类对另一个类的依赖应该建立在最小的接口上先看一张图: 类A通过接口Interface1 依赖类B,类C通过接口Interface1 依赖类D,如果接口Interface1对于类A和类C来说不是最小接口,那么类…...
BD202311夏日漫步(最少步数,BFS或者 Dijstra)
本题链接:码蹄集 题目: 夏日夜晚,小度看着庭院中长长的走廊,萌发出想要在上面散步的欲望,小度注意到月光透过树荫落在地砖上,并且由于树荫的遮蔽度不通,所以月光的亮度不同,为了直…...

React - 你知道props和state之间深层次的区别吗
难度级别:初级及以上 提问概率:60% 如果把React组件看做一个函数的话,props更像是外部传入的参数,而state更像是函数内部定义的变量。那么他们还有哪些更深层次的区别呢,我们来看一下。 首先说props,他是组件外部传入的参数,我们知道…...
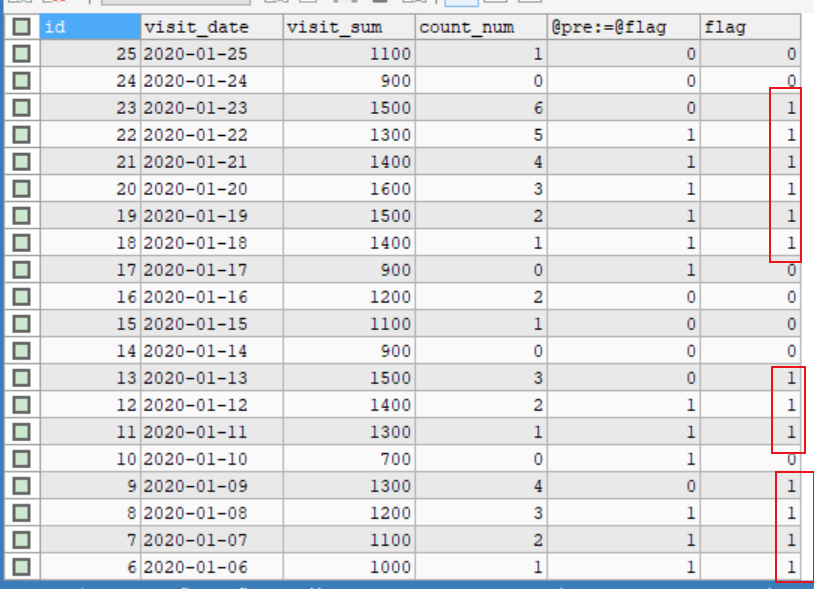
mysql 查询实战-变量方式-解答
对mysql 查询实战-变量方式-题目,进行一个解答。(先看题,先做,再看解答) 1、查询表中⾄少连续三次的数字 1,处理思路 要计算连续出现的数字,加个前置变量,记录上一个的值,…...

SpringBoot3配置SpringSecurity6
访问1:localhost:8080/security,返回:需要先认证才能访问(说明没有权限) 访问2:localhost:8080/anonymous,返回:anonymous(说明正常访问) 相关文件如下&…...
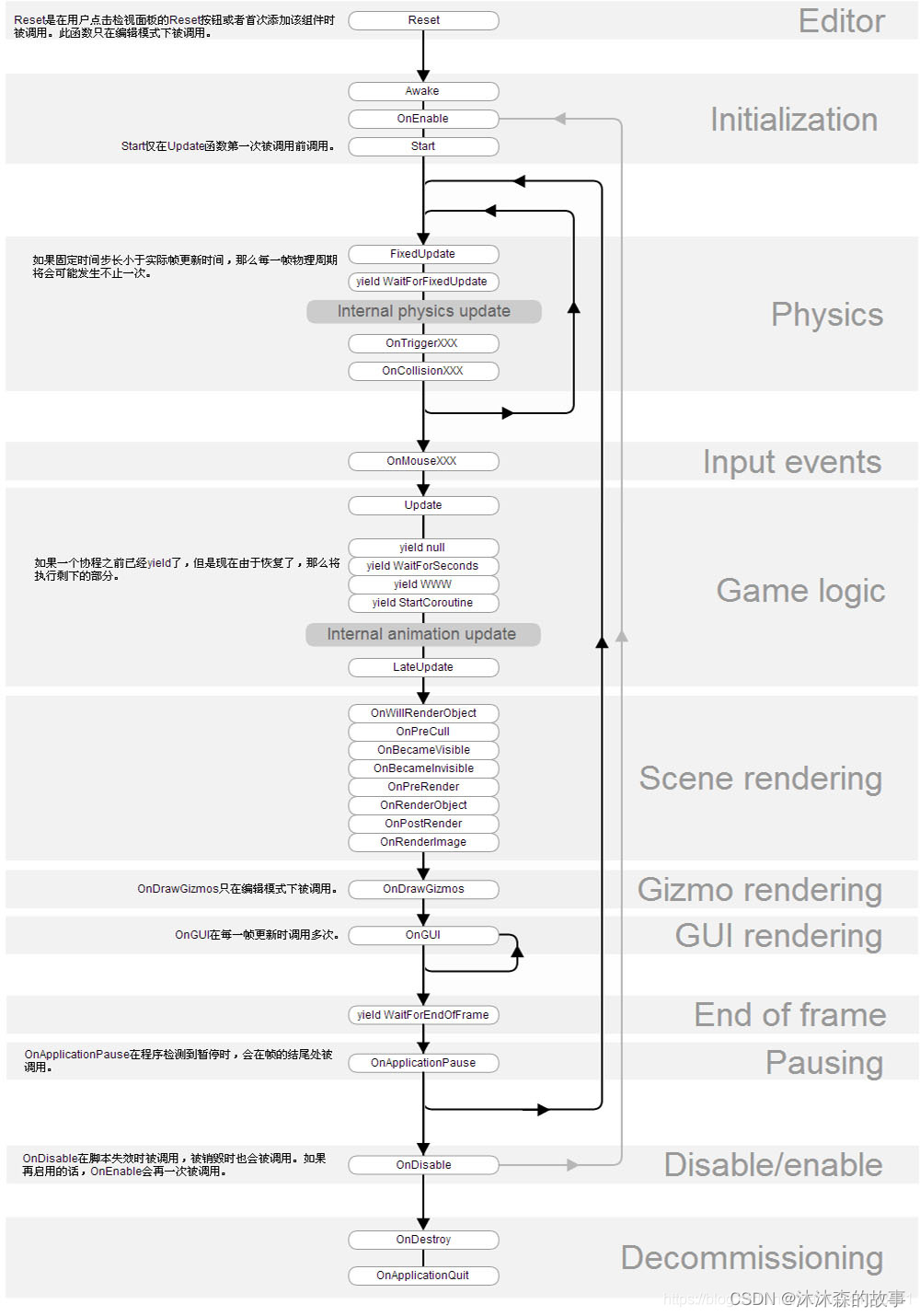
Unity之Unity面试题(三)
内容将会持续更新,有错误的地方欢迎指正,谢谢! Unity之Unity面试题(三) TechX 坚持将创新的科技带给世界! 拥有更好的学习体验 —— 不断努力,不断进步,不断探索 TechX —— 心探索、心进取…...
)
Linux命令-dos2unix命令(将DOS格式文本文件转换成Unix格式)
说明 dos2unix命令 用来将DOS格式的文本文件转换成UNIX格式的(DOS/MAC to UNIX text file format converter)。DOS下的文本文件是以 \r\n 作为断行标志的,表示成十六进制就是0D0A。而Unix下的文本文件是以\n作为断行标志的,表示成…...

企业怎么做数据分析
数据分析在当今信息化时代扮演着至关重要的角色。能够准确地收集、分析和利用数据,对企业的决策和发展都具有重要意义。数聚将介绍企业如何合理地利用数据分析,如何协助企业在竞争激烈的市场中取得优势。 一、建立完善的数据收集系统 在进行数据分析之…...

1111111111
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm1001.2014.3001.5343 给大家分享一句我很喜欢我话: 知不足而奋进,望远山而前行&am…...
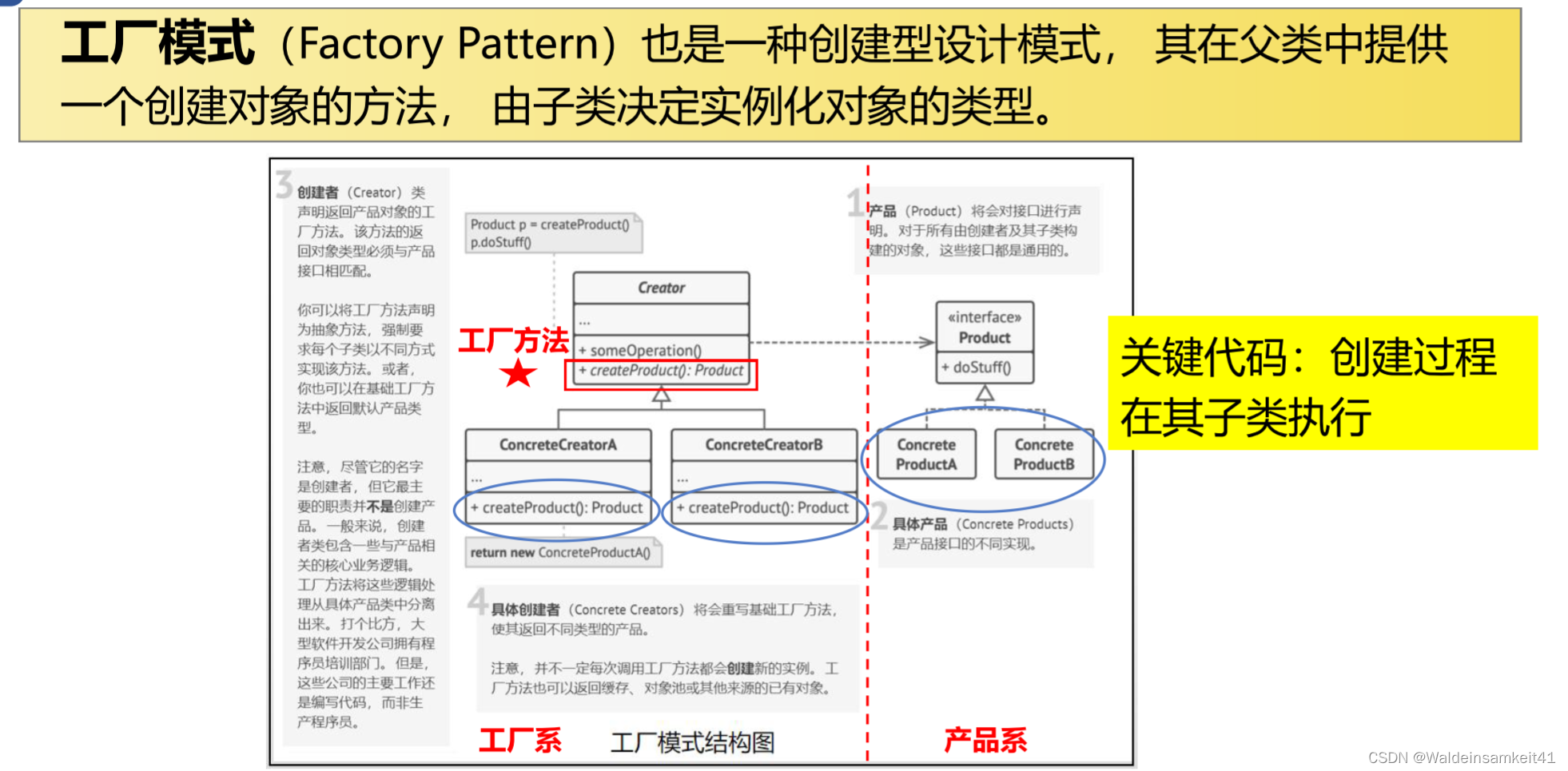
[面向对象] 单例模式与工厂模式
单例模式 是一种创建模式,保证一个类只有一个实例,且提供访问实例的全局节点。 工厂模式 面向对象其中的三大原则: 单一职责:一个类只有一个职责(Game类负责什么时候创建英雄机,而不需要知道创建英雄机要…...
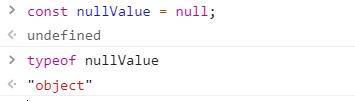
《前端防坑》- JS基础 - 你觉得typeof nullValue === null 么?
问题 JS原始类型有6种Undefined, Null, Number, String, Boolean, Symbol共6种。 在对原始类型使用typeof进行判断时, typeof stringValue string typeof numberValue number 如果一个变量(nullValue)的值为null,那么typeof nullValue "?" const u …...
【项目实战经验】DataKit迁移MySQL到openGauss(下)
上一篇我们分享了安装、设置、链接、启动等步骤,本篇我们将继续分享迁移、启动~ 目录 9. 离线迁移 9.1. 迁移插件安装 中断安装,比如 kill 掉java进程(安装失败也要等待300s) 下载安装包准备上传 缺少mysqlclient lib包 mysq…...
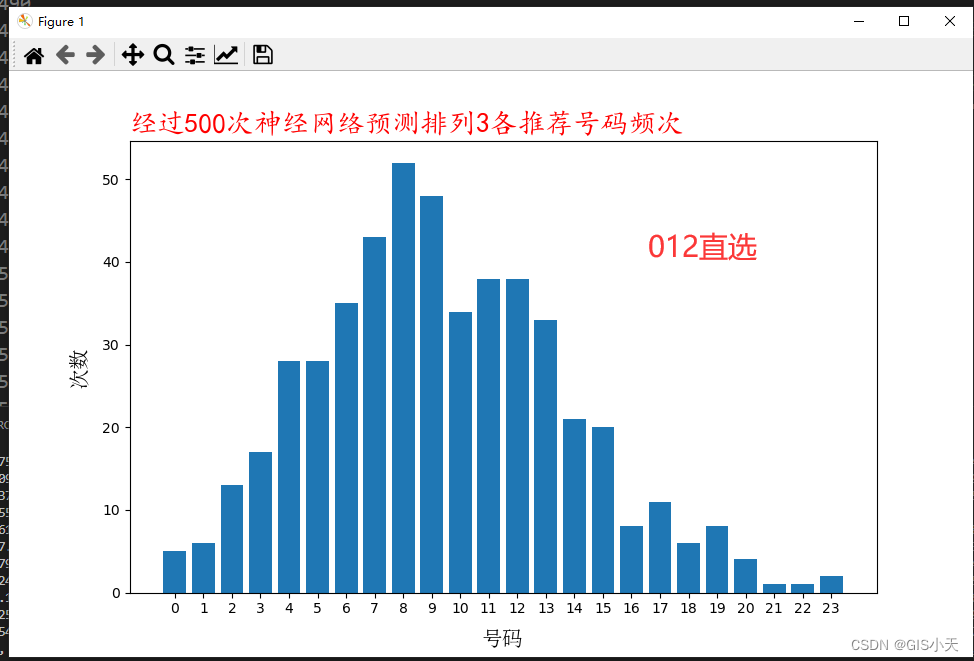
AI预测体彩排3第2弹【2024年4月13日预测--第1套算法开始计算第2次测试】
各位小伙伴,今天实在抱歉,周末回了趟老家,回来比较晚了,数据今天上午跑完后就回老家了,晚上8点多才回来,赶紧把预测结果发出来吧,虽然有点晚了,但是咱们前面说过了,目前的…...
2024年4月串讲题组一)
【13137】质量管理(一)2024年4月串讲题组一
目录 1.选择题 2.多选题 3.简答题 4.论述题 5.计算题 6.论述题 【13137】质量管理-速 记 宝 典【全国通用】</...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
