【C++算法竞赛 · 图论】图的存储
前言
图的存储
邻接矩阵
方法
复杂度
应用
例题
题解
邻接表
方法
复杂度
应用
前言
上一篇文章中(【C++算法竞赛 · 图论】图论基础),介绍了图论相关的概念和一种图的存储的方法,这篇文章将会介绍剩下的两种方法,话不多说,步入正题——
图的存储
邻接矩阵
方法
使用一个二维数组 G 来存边,其中 G[u][v] 为 1 表示存在 u 到 v 的边,为 0 表示不存在。如果是带边权的图,可以在 G[u][v] 中存储 u 到 v 的边的边权。
复杂度
查询是否存在某条边:O(1) 。
遍历一个点的所有出边:O(n) 。
遍历整张图:。
空间复杂度:。
应用
邻接矩阵只适用于没有重边(或重边可以忽略)的情况。
其最显著的优点是可以 O(1) 查询一条边是否存在。
由于邻接矩阵在稀疏图上效率很低(尤其是在点数较多的图上,空间无法承受),所以一般只会在稠密图上使用邻接矩阵。
例题
题目描述
给定一张 N 个顶点 M 条边的简单无向图。顶点编号为 1 ... N。
第 i 条边 (1 <= i <= M) 连接顶点 U_i 和顶点 V_i 。
请求出满足以下所有条件的三元组 (a, b, c) 组的总数。
- 1 <= a, b, c <= N
- 存在连接顶点 a 和顶点 b 的边。
- 存在连接顶点 a 和顶点 c 的边。
- 存在连接顶点 b 和顶点 c 的边。
3 <= N <= 100
输入格式
N M
U_1 V_1
...
U_M V_M
输出格式
输出答案。
样例
输入样例 1
5 6
1 5
4 5
2 3
1 4
3 5
2 5输出样例 1
2
输入样例 2
3 1
1 2
输出样例 2
0
输入样例 3
7 10
1 7
5 7
2 5
3 6
4 7
1 5
2 4
1 3
1 6
2 7输出样例 3
4
题解
这题很简单,直接用二维数组去存储,然后枚举三个节点(数据量很小)判断是否都有边连接就行了。
#include <bits/stdc++.h>
using namespace std;int G[110][110];int main() {memset(G, 0, sizeof(G));int n, m;cin >> n >> m;for (int i = 0; i < m; i++) {int u, v;cin >> u >> v;G[u][v] = 1;G[v][u] = 1;}int cnt = 0;for (int a = 1; a <= n; a++) {for (int b = a + 1; b <= n; b++) {for (int c = b + 1; c <= n; c++) {if (G[a][b] == 1 && G[a][c] == 1 && G[b][c] == 1) {cnt++;}}}}cout << cnt;return 0;
}邻接表
方法
使用一个支持动态增加元素的数据结构构成的数组,如 vector<int> adj[n + 1] 来存边,其中 adj[u] 存储的是点 u 的所有出边的相关信息(终点、边权等)。
复杂度
查询是否存在 u 到 v 的边:(如果事先进行了排序就可以使用 二分查找 做到
)。
遍历点 u 的所有出边:![]() 。
。
遍历整张图:。
空间复杂度:。
应用
存各种图都很适合,除非有特殊需求(如需要快速查询一条边是否存在,且点数较少,可以使用邻接矩阵)。
尤其适用于需要对一个点的所有出边进行排序的场合。
本文就到这里了,如果有帮助的话,记得点赞收藏!下次再见啦!
相关文章:
【C++算法竞赛 · 图论】图的存储
前言 图的存储 邻接矩阵 方法 复杂度 应用 例题 题解 邻接表 方法 复杂度 应用 前言 上一篇文章中(【C算法竞赛 图论】图论基础),介绍了图论相关的概念和一种图的存储的方法,这篇文章将会介绍剩下的两种方法ÿ…...

Spring AOP IOC
spring的优缺点 IOC集中管理对象,对象之间解耦,方便维护对象AOP在不修改原代码的情况下,实现一些拦截提供众多辅助类,方便开发方便集成各种优秀框架 紧耦合和松耦合 松耦合可以使用单一职责原则、接口分离原则、依赖倒置原则 …...
 1.1 编译QEMU 构建RISC-V64架构 运行Linux kernel)
Linux ARM平台开发系列讲解(QEMU篇) 1.1 编译QEMU 构建RISC-V64架构 运行Linux kernel
1. 概述 QEMU可以模拟很多架构的CPU(ARM,RISC-V等),重点是免费,用来学Linux简直太适合不过了,所以,我打算开一章节来教QEMU的使用,这样也方便环境统一调试,本章节就讲解如何在Ubuntu搭建QEMU,我的环境是全新的Ubuntu22,QEMU下载的9.0,kernel下载的6.0. 2. 源码下载…...
Day19-【Java SE进阶】网络编程
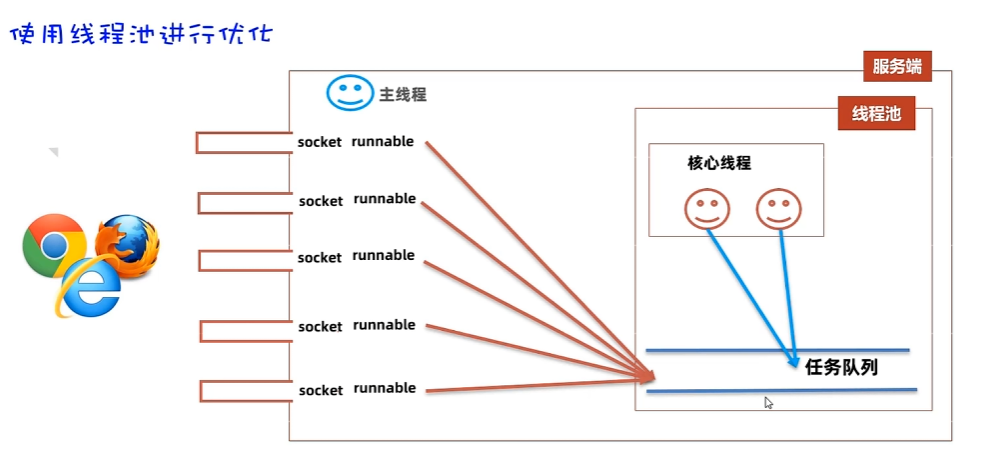
一、网络编程 1.概述 可以让设备中的程序与网络上其他设备中的程序进行数据交互(实现网络通信的)。java.net,*包下提供了网络编程的解决方案! 基本的通信架构 基本的通信架构有2种形式:CS架构(Client客户端/Server服务端)、BS架构(Browser浏览器/Server服务端)。 网络通信的…...

pyqt写个星三角降压启动方式2
星三角降压启动用可以用类进行封装,就像博图FB块那样。把逻辑都在类里完成,和外界需要交互的暴露出接口。测试过程中,发现类中直接用定时器QTimer会出现问题。然后就把定时器放到外面了。然后测试功能正常。 from PySide6.QtWidgets import …...
js可视化爬取数据生成当前热点词汇图
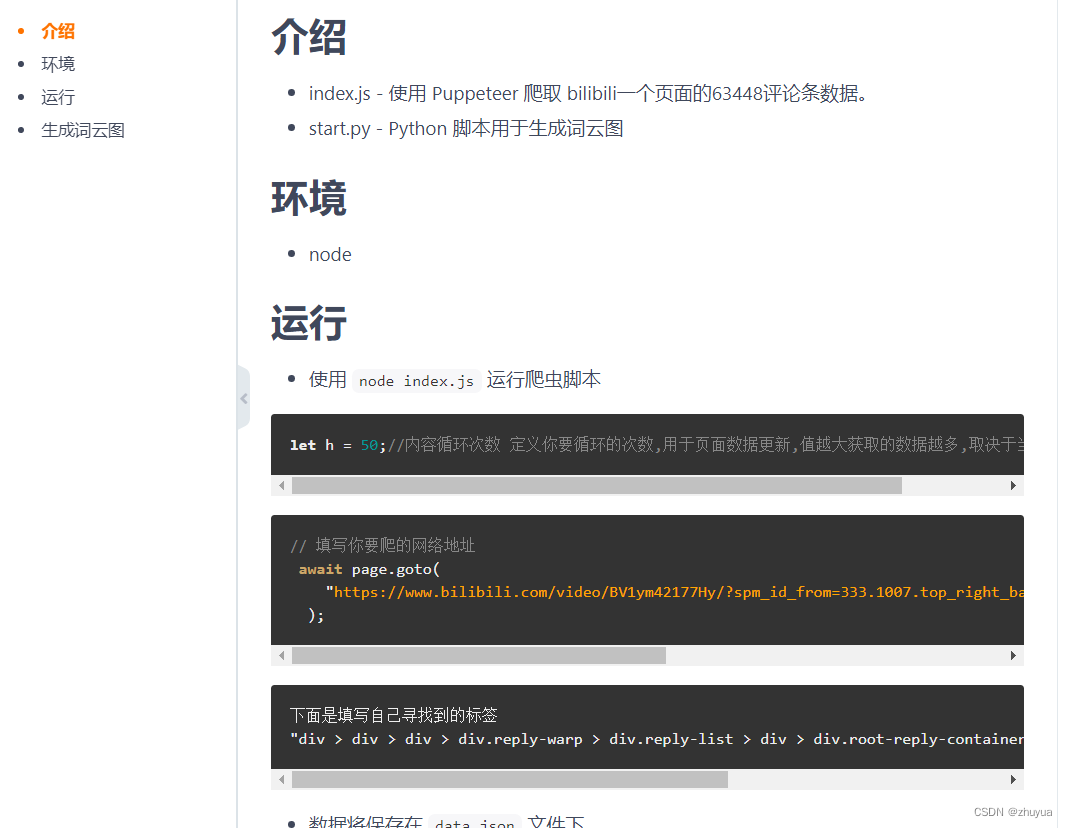
功能 可以爬取到很多数据,并且生成当前的热点词汇图,词越大越热门(词云图) 这里以b站某个评论区的数据为例,爬取63448条数据生成这样的图片 让我们能够更加直观的看到当前的热点 git地址 可以直接使用,中文…...
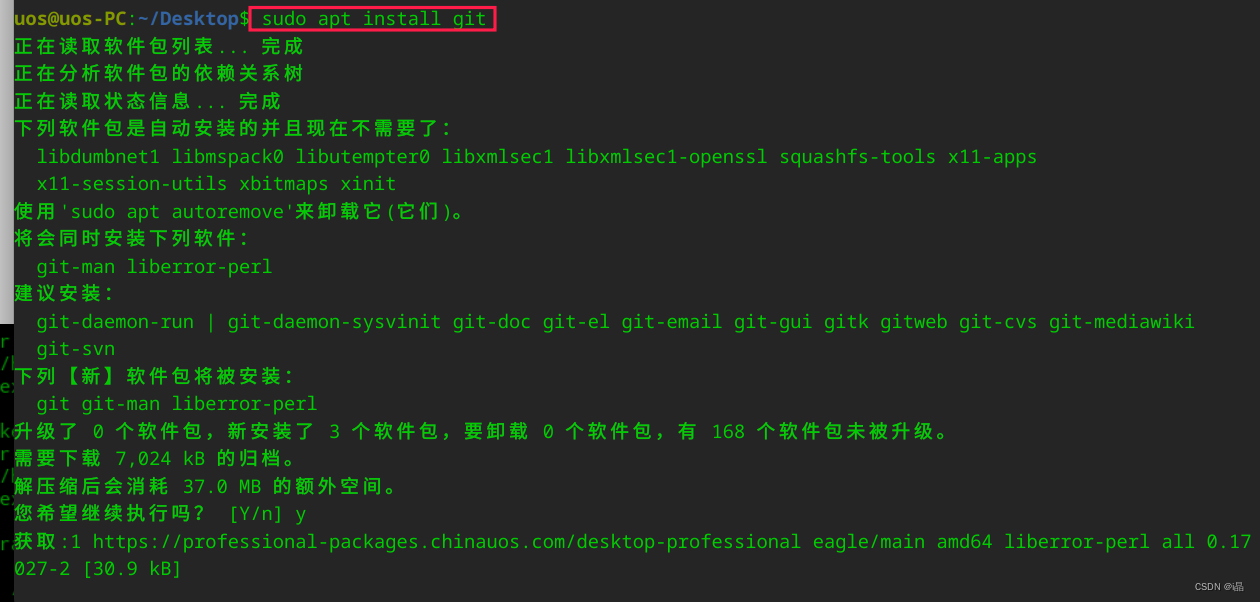
研发岗-面临统信UOS系统配置总结
第一步 获取root权限 配置环境等都需要用到root权限,所以我们先获取到root权限,方便下面的操作 下载软件 在UOS应用商店下载的所需应用 版本都比较低 安装node 官网下载了【arm64】的包,解压到指定文件夹,设置链接࿰…...
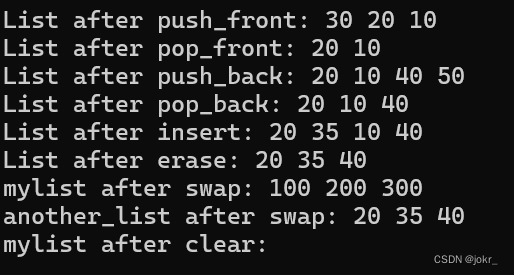
【STL详解 —— list的介绍及使用】
STL详解 —— list的介绍及使用 list的介绍list的介绍使用list的构造list iterator的使用list capacitylist element accesslist modifiers 示例list的迭代器失效 list的介绍 list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭…...

cocos creator开发中遇到的问题和解决方案
前言 总结一下使用cocos开发遇到的坑,不定期更新。 问题汇总 代码修改Position坐标不生效 首先要通过打log或者断点排除下是不是逻辑上的问题,还有是不是有动画相关把位置修改了。我遇到的问题是坐标修改被widget组件覆盖了。 纹理压缩包体变大 co…...

10分钟带你学会配置DNS服务正反向解析
正向解析 服务端IP客户端IP网址192.168.160.134192.168.160.135www.openlab.com 一、首先做准备工作: 关闭安全软件,关闭防火墙,下载bind软件 [rootserver ~]# setenforce 0 [rootserver ~]# systemctl stop firewalld [rootserver ~]# y…...

【vim 学习系列文章 19 -- 映射快捷键调用两个函数 A 和B】
请阅读【嵌入式开发学习必备专栏 之 Vim】 文章目录 映射快捷键调用两个函数 映射快捷键调用两个函数 在 Vim 中,如果想通过按下 gcm 来调用两个函数,比如 FunctionA 和 FunctionB,需要先定义这两个函数,然后创建一个映射。这个映…...

Windows安装MongoDB结合内网穿透轻松实现公网访问本地数据库
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

sgg大数据全套技术链接[plus]
写在开头:感谢尚硅谷,尚硅谷万岁,我爱尚硅谷 111个技术栈43个项目,兄弟们,冲! 最近小米又又又火了一把,致敬所有造福人民的企业和伟大的企业家,致敬雷军,小米ÿ…...

OpenHarmony南向嵌入式:【XR806开发板指导文档】
一. 简介 芯片介绍 XR806是全志科技旗下子公司广州芯之联研发设计的一款支持WiFi和BLE的高集成度无线MCU芯片,支持OpenHarmony轻量设置系统。具有集成度高、硬件设计简单、BOM成本低、安全可靠等优点。可广泛满足 智能家居、智慧楼宇、工业互联、儿童玩具、电子竞…...

Rust 实战练习 - 10. JSON、XML、YAML/TOML、Ini专题
配置文件 常见的配置文件有很多:JSON, Ini, XML, TOML, YAML … 目标: JSON/YAML/TOMLIniXML Rust中序列化用的最多的是 serde, 依赖它,有很多出色的第三方库可以使用。 其中,serde本身支持JSON/YAML/TOML/JSON5…多种&#…...

5.Hexo为页面标记标签和类别
Hexo的标签和类别基本上是可以在Hexo中将内容分组的两种方式 如果在网站上有一堆内容,有不同的博客文章 将博客文章分类为不同的类别会很有帮助 用特定的关键词为博客文章标记 如果可以同时分类和标记页面,会使网站用户更轻松地找到他们想要的页面类型 …...

·13·1dawwd
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm1001.2014.3001.5343 给大家分享一句我很喜欢我话: 知不足而奋进,望远山而前行&am…...

Docker - PostgreSQL
博文目录 文章目录 说明命令 说明 Docker Hub PostgreSQL 数据卷数据卷印射在容器内的路径postgres/var/lib/postgresql/data |容器内的路径|说明| |–|–|–| |/var/lib/postgresql/data|数据目录| 部分环境变量是否必要说明POSTGRES_PASSWORD必需设置超级用户密码POSTGRES…...
Python | Leetcode Python题解之第26题删除有序数组中的重复项
题目: 题解: class Solution:def removeDuplicates(self, nums: List[int]) -> int:if not nums:return 0n len(nums)fast slow 1while fast < n:if nums[fast] ! nums[fast - 1]:nums[slow] nums[fast]slow 1fast 1return slow...

【电控笔记4】拉普拉斯-传递函数-pid
数据标幺化 拉普拉斯变换 欧拉公式 常见s变换 s变换性质...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
