【状态压缩 容斥原理 组合数学】100267. 单面值组合的第 K 小金额
本文涉及知识点
状态压缩 容斥原理 组合数学
二分查找算法合集
LeetCode100267. 单面值组合的第 K 小金额
给你一个整数数组 coins 表示不同面额的硬币,另给你一个整数 k 。
你有无限量的每种面额的硬币。但是,你 不能 组合使用不同面额的硬币。
返回使用这些硬币能制造的 第 kth 小 金额。
示例 1:
输入: coins = [3,6,9], k = 3
输出: 9
解释:给定的硬币可以制造以下金额:
3元硬币产生3的倍数:3, 6, 9, 12, 15等。
6元硬币产生6的倍数:6, 12, 18, 24等。
9元硬币产生9的倍数:9, 18, 27, 36等。
所有硬币合起来可以产生:3, 6, 9, 12, 15等。
示例 2:
输入:coins = [5,2], k = 7
输出:12
解释:给定的硬币可以制造以下金额:
5元硬币产生5的倍数:5, 10, 15, 20等。
2元硬币产生2的倍数:2, 4, 6, 8, 10, 12等。
所有硬币合起来可以产生:2, 4, 5, 6, 8, 10, 12, 14, 15等。
提示:
1 <= coins.length <= 15
1 <= coins[i] <= 25
1 <= k <= 2 * 109
coins 包含两两不同的整数。
容斥原理:小于等于mid的金额数量
如果不考虑重复 ∑ i : n − 1 m i d / c o i n s [ i ] \sum_{i:}^{n-1}mid/coins[i] ∑i:n−1mid/coins[i] 考虑重复则很复杂。
以mid 12为例子,f(x) 表示用面值x的金币能过组成小于等于mid的金额数量:
a , coins = {2,3}
面值2的倍数:2,4,6,8,10,12 f(2)=6,其中重复2个。
面值3的倍数:3,6,9,12 f(3) = 4 ,重复2个。
总数量:f(2)+f(3)-f(6) = 6-4-2=8。6是最小公倍数LCM
b,coins = {2,3,5}
面值5的倍数:5,10 = 2 ,其中重复一个。
新增加的数:
f(5) - f(LCM(5,2))-f(LCM(3,5))
如果一个数 同时10和15的倍数,则减重复了,要加回来:
及:
f(5) - f(LCM(5,2))-f(LCM(3,5)) + f(LCM(2,3,5))
注意: C++有系统函数 lcm
二分
令 cnt(mid) 是小于等于mid的金额数。如果cnt(mid) < k,则mid一定不是解。我们要求第个一 cnt(mid)>=k 。 故用左开右闭空间。
单调性证明
mid1 > mid2 ,如果cnt(mid1)>=k 成立,则cnt(mid2)>=k 成立, 因为(mid1,mid2]中的数,要么让返回值+1,要么让返回值不变。同理: cnt(mid2)>=k 不成立,则cnt(mid1)>=k,也不成立。
代码
核心代码
class Solution {
public:long long findKthSmallest(vector<int>& coins, int k) {m_coins = coins; long long left = 0, right = 1'000'000'000'000LL;while (right - left > 1) {const auto mid = left + (right - left) / 2;if (Count(mid) >= k) {right = mid;}else{left = mid;}}return right;}long long Count(long long mid) {vector<vector<long long>> vMask; long long llRet = 0;for (const auto& n : m_coins) {vector<vector<long long>> vMask2;for (const auto& v : vMask) {vector<long long> v2;for (const auto& llMask : v) {const long long tmp = lcm(llMask, n);if (tmp <= mid) {v2.emplace_back(tmp);} }vMask2.emplace_back(v2);}vMask2.emplace_back();vMask2.back().emplace_back(n);for (int i = 1; i < vMask2.size(); i++) {vMask2[i].insert(vMask2[i].end(), vMask[i - 1].begin(), vMask[i - 1].end());} vMask2.swap(vMask);}for (int i = 0; i < vMask.size(); i++) {for (const auto& iMask : vMask[vMask.size() - 1 - i]) {llRet += (1 & i) ? -mid / iMask : mid / iMask;}}return llRet;}vector<int> m_coins;
};
测试用例
int main()
{vector<int> nums = { 3,6,9 };int k;{Solution sln;nums = { 2,3,5,7,11,13,17,19,23,25,20,18 }, k = 1000000000;auto res = sln.findKthSmallest(nums, k);Assert(9LL, res);}{Solution sln;nums = { 3,6,9 }, k = 3;auto res = sln.findKthSmallest(nums, k);Assert(9LL, res);}}
用状态压缩优化代码量(通过前置状态计算后置状态)
class Solution {
public:long long findKthSmallest(vector<int>& coins, int k) { const int iMaskCount = 1 << coins.size();vector<int> v01(iMaskCount),vLCM(iMaskCount,-1);vector<int> vMask[2];//vMask[0] 记录 偶数个数的最小公倍数,vMask[1]记录奇数个数的最小公倍数v01[0] = 0;vLCM[0] = 1;for (int iMask = 0; iMask < iMaskCount; iMask++) {for (int j = 0; j < coins.size(); j++) {if (!((1 << j) & iMask)) {const int iNewMask = (1 << j) | iMask;if (-1 != vLCM[iNewMask]) { continue; }v01[iNewMask] = v01[iMask] ^ 1;vLCM[iNewMask] = lcm(vLCM[iMask], coins[j]);vMask[v01[iNewMask]].emplace_back(vLCM[iNewMask]); }}}long long left = 0, right = 1'000'000'000'000LL;while (right - left > 1) {const auto mid = left + (right - left) / 2;long long cnt = 0;for (const auto& ll : vMask[0]) {cnt -= mid / ll;}for (const auto& ll : vMask[1]) {cnt += mid / ll;}if (cnt >= k) {right = mid;}else{left = mid;}}return right;}
};
用状态压缩优化代码量(计算后置状态)
class Solution {
public:long long findKthSmallest(vector<int>& coins, int k) { const int iMaskCount = 1 << coins.size(); vector<long long> vMask[2];//vMask[0] 记录 偶数个数的最小公倍数,vMask[1]记录奇数个数的最小公倍数vector<long long> v01(iMaskCount), vLCM(iMaskCount, -1);{ v01[0] = 0;vLCM[0] = 1;for (int i = 0; i < coins.size(); i++) {vLCM[1 << i] = coins[i];}for (int iNewMask = 1; iNewMask < iMaskCount; iNewMask++) {const int iMask = (iNewMask - 1) & iNewMask;v01[iNewMask] = v01[iMask] ^ 1;vLCM[iNewMask] = lcm(vLCM[iMask], vLCM[iNewMask - iMask]);vMask[v01[iNewMask]].emplace_back(vLCM[iNewMask]);}}long long left = 0, right = 1'000'000'000'000LL;while (right - left > 1) {const auto mid = left + (right - left) / 2;long long cnt = 0;for (const auto& ll : vMask[0]) {cnt -= mid / ll;}for (const auto& ll : vMask[1]) {cnt += mid / ll;}if (cnt >= k) {right = mid;}else{left = mid;}}return right;}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【状态压缩 容斥原理 组合数学】100267. 单面值组合的第 K 小金额
本文涉及知识点 状态压缩 容斥原理 组合数学 二分查找算法合集 LeetCode100267. 单面值组合的第 K 小金额 给你一个整数数组 coins 表示不同面额的硬币,另给你一个整数 k 。 你有无限量的每种面额的硬币。但是,你 不能 组合使用不同面额的硬币。 返回…...

.net框架和c#程序设计第三次测试
目录 一、测试要求 二、实现效果 三、实现代码 一、测试要求 二、实现效果 数据库中的内容: 使用数据库中的账号登录: 若不是数据库中的内容: 三、实现代码 login.aspx文件: <% Page Language"C#" AutoEventW…...
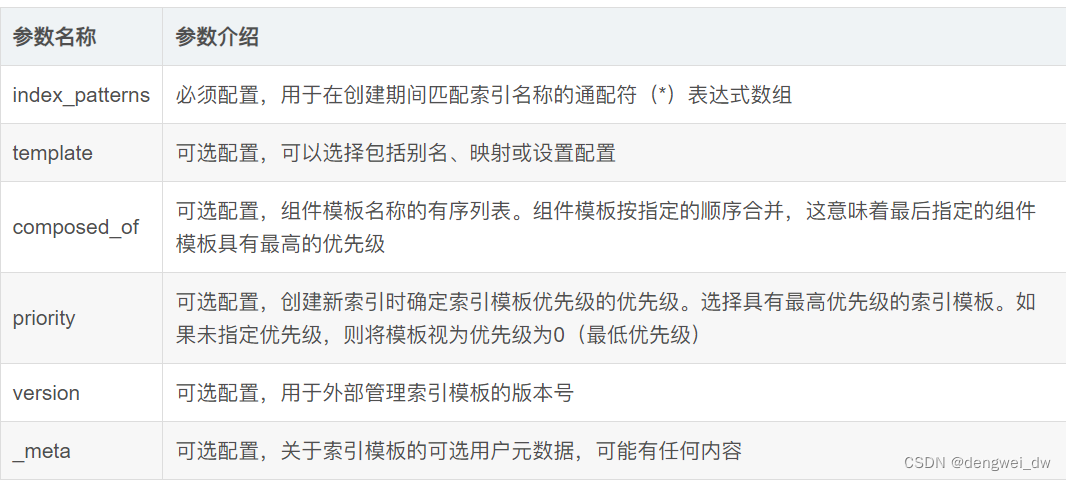
架构师系列-搜索引擎ElasticSearch(五)- 索引设计
索引创建后,要非常谨慎,创建不好后面会出现各种问题。 索引设计的重要性 索引创建后,索引分片只能通过_split和_shrink 接口对其进行成倍的增加和缩减。 ES的数据是通过_routing分配到各个分片上的,所以本质上不推荐区改变索引的…...

kafka ----修改log4j、jmx、jvm参数等
1、修改log4j 日志路径 在kafka-run-class.sh文件中修改如下配置,将 LOG_DIR变量指定为自己想要存储的路径 # Log directory to use if [ "x$LOG_DIR" "x" ]; thenLOG_DIR"$base_dir/logs" fi2、修改jmx参数 在kafka-run-class.s…...
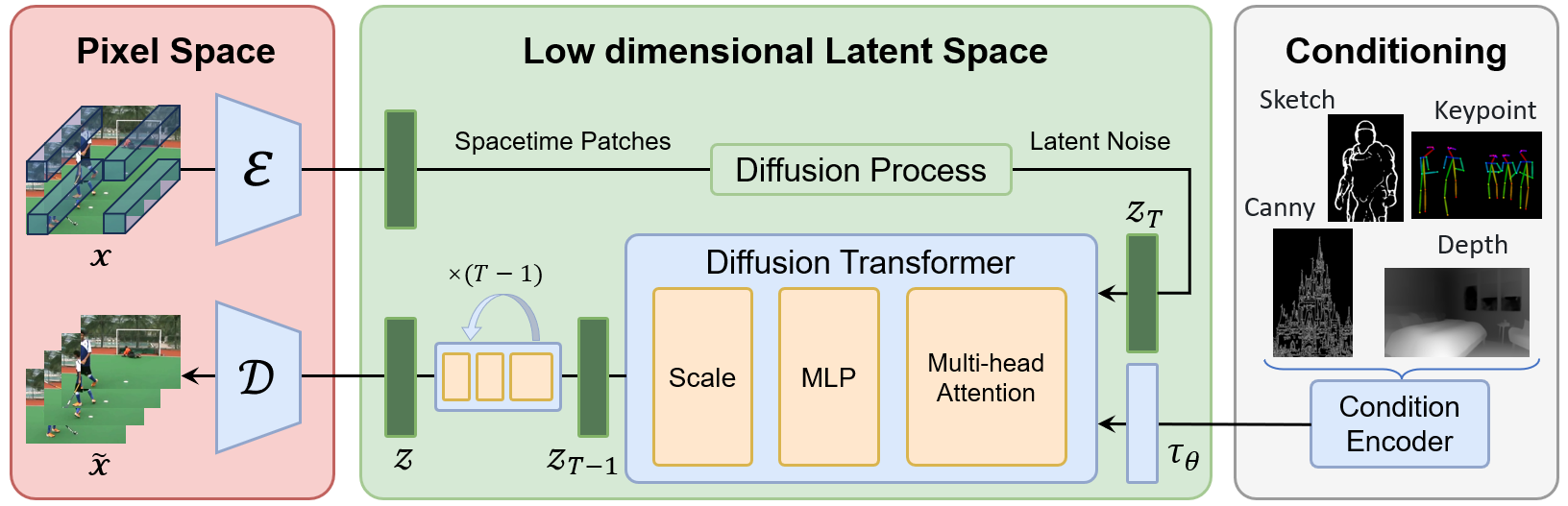
Python 全栈 Web 应用模板:成熟架构,急速开发 | 开源日报 No.223
tiangolo/full-stack-fastapi-template Stars: 15.6k License: MIT full-stack-fastapi-template 是一个现代化的全栈 Web 应用模板。 使用 FastAPI 构建 Python 后端 API。使用 SQLModel 进行 Python SQL 数据库交互(ORM)。Pydantic 用于数据验证和设…...
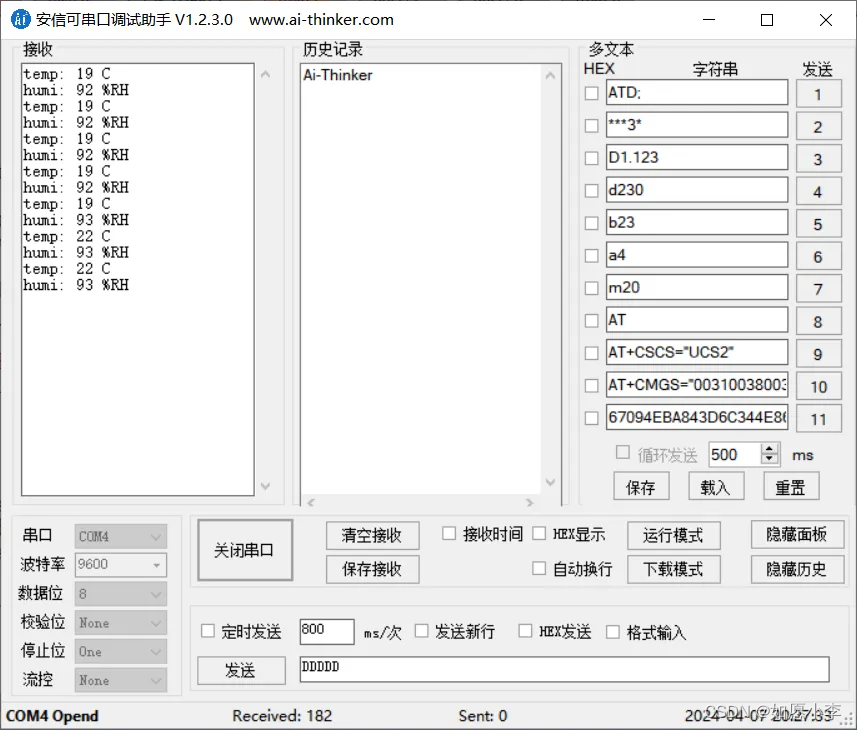
STM32之DHT11温湿度传感器
目录 一 DHT11温湿度传感器简介 1.1 传感器特点 1.2 传感器特性 1.3 传感器引脚说明 二 测量原理及方法 2.1 典型应用电路 2.2 单线制串行简介 2.2.1 串行接口 (单线双向) 2.2.2 数据示例 2.3 通信时序 三 单片机简介 3.1 STM32F103C8T6最小系统板 四 接线说明 …...

paddle ocr
paddle安装教程,git clone xxxgit https://blog.csdn.net/Castlehe/article/details/117356343 只有paddle 1.x 的教程:https://github.com/PaddlePaddle/PaddleOCR/blob/static/doc/doc_en/quickstart_en.md 报错是因为安装的是paddle 2.x而教程只给了…...

Xcode 15.0 新 #Preview 预览让 SwiftUI 界面调试更加悠然自得
概览 从 Xcode 15 开始,苹果推出了新的 #Preview 宏预览机制,它无论从语法还是灵活性上都远远超过之前的预览方式。#Preview 不但可以实时预览 SwiftUI 视图,而且对 UIKit 的界面预览也是信手拈来。 想学习新 #Preview 预览的一些超实用调试…...
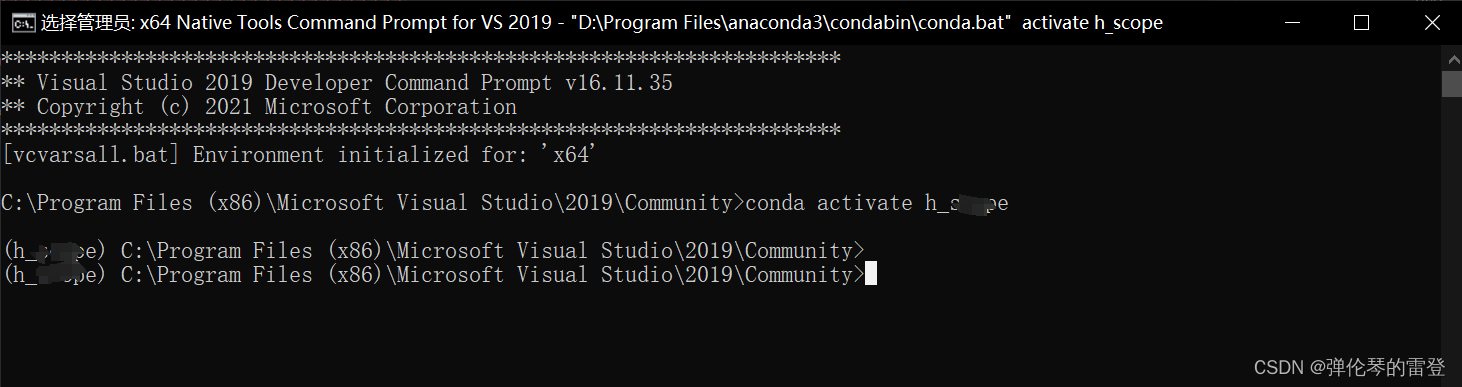
【VS2019】x64 Native Tools Command Prompt for Vs 2019使用conda命令进入环境
【VS2019】x64 Native Tools Command Prompt for Vs 2019使用conda命令进入环境 安装完VS2019后,打开终端x64 Native Tools Command Prompt for Vs 2019,直接运行conda会出现‘conda’ 不是内部或外部命令,也不是可运行的程序 原因分析&am…...

网络篇09 | 运输层 udp
网络篇09 | 运输层 udp 01 简介UDP 是面向报文的 02 报文协议 01 简介 UDP 只在 IP 的数据报服务之上增加了一些功能:复用和分用、差错检测 UDP 的主要特点:无连接。发送数据之前不需要建立连接。 使用尽最大努力交付。即不保证可靠交付。 面向报文。…...
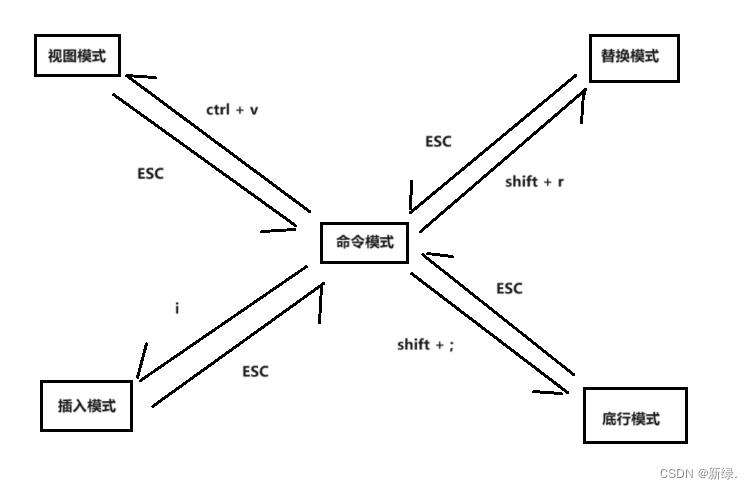
vim相关指令
vim的各种模式及其转换关系图 vim 默认处于命令模式!!! 模式之间转换的指令 除【命令模式】之外,其它模式要切换到【命令模式】,只需要无脑 ESC 即可!!! [ 命令模式 ] 切换至 [ 插…...

STM32常见调试工具介绍
STM32的常见调试工具主要包括ST-LINK、USB转TTL、USB转485以及USB转CAN。这些工具在嵌入式系统开发、调试以及通信中发挥着重要的作用。 1.ST-LINK: ST-LINK是STMicroelectronics公司专为其STM32系列微控制器开发的调试和编程工具。既能仿真也能将编译好的程序下载…...

简历上写熟悉Linux下常用命令?直接寄
大家写简历技术栈时,都觉得越多越好,其中一条,熟悉Linux下常用命令?其实开发中Linux不是必备考点,除了运维,真正用的多的仅仅cd ls mkdir等,但当面试官问到上面命令时,是不是就傻眼了…...

【设计模式】4、prototype 原型模式
四、prototype 原型模式 https://refactoringguru.cn/design-patterns/prototype 如果希望 复制对象, 可使用 “prototype 模式” 如果 “待复制的对象” 是 interface 而不是 class, 或者如果 class 有 private 变量时. 无法知道 "待复制的对象"的细节, 则需要其…...

ES6 关于Class类的继承 extends(2024-04-10)
1、简介 类Class 可以通过extends关键字实现继承,让子类继承父类的属性和方法。extends 的写法比 ES5 的原型链继承,要清晰和方便很多。 class Foo {constructor(x, y) {this.x x;this.y y;console.log(父类构造函数)}toString() {return ( this.x …...

边缘计算【智能+安全检测】系列教程--使用OpenCV+GStreamer实现真正的硬解码,完全消除马赛克
通过现有博客的GST_URL = "rtspsrc location=rtsp://admin:abcd1234@192.168.1.64:554/h264/ch01/main/av_stream latency=150 ! rtph264depay ! avdec_h264 ! videorate ! videoconvert ! appsink sync=false" GStreamer的解码方式解码,大多情况应该存在上图马赛克…...

Anaconda在Ubuntu下的安装与简单使用
一、参考资料 ubuntu16.04下安装&配置anacondatensorflow新手教程 二、安装Anaconda 下载 Miniconda镜像1 or Miniconda镜像2 # 下载 wget Miniconda3-py39_4.10.3-Linux-x86_64.sh# 安装 bash Miniconda3-py39_4.10.3-Linux-x86_64.sh一路yes 安装过程中的选项 Do you …...

网络编程【InetAddress , TCP 、UDP 、HTTP 案例】
day38上 网络编程 InetAddress 理解:表示主机类 一个域名 对应 多个IP地址 public static void main(String[] args) throws UnknownHostException {//获取本机的IP地址 // InetAddress localHost InetAddress.getLocalHost(); // System.out.println(localHos…...
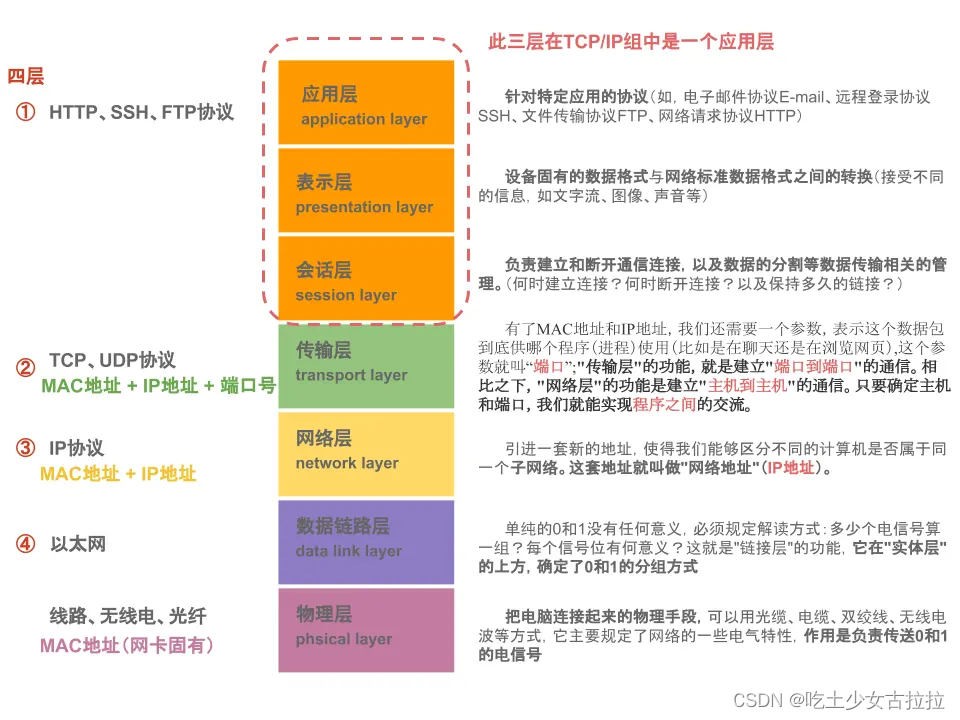
软考中级工程师网络技术第二节网络体系结构
OSPF将路由器连接的物理网络划分为以下4种类型,以太网属于(25),X.25分组交换网属于(非广播多址网络NBMA)。 A 点对点网络 B 广播多址网络 C 点到多点网络 D 非广播多址网络 试题答案 正确答案: …...
Mac 软件清单
~自留备用~ Macbook用了几年之后, 512G的内置硬盘有些紧张了, 这几天总是提示空间不足, 就重装了下系统, 重装之后竟然不记得有些软件的名字和下载链接, 特此记录 Office 办公套件 直接从微软官网下载Office 安装包https://officecdnmac.microsoft.com/pr/C1297A47-86C4-4C1F…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
