【刷题笔记】第三天
两道简单题
文章目录
- [2923. 找到冠军 I](https://leetcode.cn/problems/find-champion-i/description/)
- [3095. 或值至少 K 的最短子数组 I](https://leetcode.cn/problems/shortest-subarray-with-or-at-least-k-i/description/)
2923. 找到冠军 I
方法1:
如果 i 是冠军,那么 grid[i][j] == 1, 其中j!=i
所以我们遍历grid的每一行,假设是第i行,只要除第i列外,其他位置的元素都是1,则 i 就是冠军。
除了判断每一行,也可以判断每一列,只要这一列的所有元素都为0,说明没有队伍可以战胜该队伍。
class Solution {public int findChampion(int[][] grid) {for (int i = 0; i < grid.length; ++i) {boolean flag = true; // 记录是否决出了冠军for (int j = 0; j < grid[i].length; ++j) {if (j != i && grid[i][j] == 0) {flag = false; // j比i强,i不可能是冠军break;}}if (flag) {return i;}}return -1;}
}
时间复杂度 O ( n 2 ) O(n^2) O(n2)
方法2:擂主争霸
class Solution {public int findChampion(int[][] grid) {int champinon = 0; // 假设0是冠军int index = 1;int n = grid.length;while (index < n) {if (grid[index][champinon] == 1) {// index比champinon,所以冠军变为indexchampinon = index;}// 冠军变了,为什么index不需要从0开始?// 因为在1~index - 1都不能战胜原来的冠军,当然更战胜不了当前的冠军(当前的冠军战胜了原来的冠军)index++;}return champinon;}
}
时间复杂度 O(n)
3095. 或值至少 K 的最短子数组 I
3097. 或值至少为 K 的最短子数组 II
两道题区别只是数据规模不同
方法1:
暴力枚举每一个子数组
class Solution {public int minimumSubarrayLength(int[] nums, int k) {int ans = Integer.MAX_VALUE;for (int i = 0; i < nums.length; ++i) {int res = 0;for (int j = i; j < nums.length; ++j) {res |= nums[j];if (res >= k) {ans = Math.min(ans, j - i + 1);break;}}}return ans == Integer.MAX_VALUE ? -1 : ans;}
}
方法2:
遇到到子数组考虑以i结尾的子数组……
或的性质:越或,值越大或者不变,肯定不能变小。
考虑以i结尾的子数组,当i-1结尾的子数组的或值 |nums[i] ,就是i结尾的子数组的或值。
为了计算最短子数组的长度,在保存或值的同时,记录该或值对应的左端点位置。如果遇到相同的或值,就保留最大的左端点。
还有一些coding细节,例如如何利用一个list,动态的更新当前子数组的或值,下面代码用到了双指针思想。
class Solution {public int minimumSubarrayLength(int[] nums, int k) {// list中的元素按照左端点位置从小到大排序List<int[]> list = new ArrayList<>();// 保存以i结尾的子数组的{or值,对应的最大左端点}int n = nums.length;int ans = Integer.MAX_VALUE;for (int i = 0; i < n; ++i) {list.add(new int[]{0, i}); // 先占个位,不参与或运算// 此时,list是以i-1结尾的子数组的or值及其左端点位置int l = 0, r = 0;// 将list中的元素或上nums[i]for (; r < list.size(); ++r) {int[] cur = list.get(r);cur[0] |= nums[i];if (cur[0] >= k) {// 满足条件就收集结果ans = Math.min(ans, i - cur[1] + 1);}if (cur[0] == list.get(l)[0]) {// 有重复值,保留左端点最大的list.get(l)[1] = cur[1]; // 左端点更新为最大的} else {list.set(++l, cur); // 将l+1位置覆盖}}// 以i结尾的子数组对应的或值,其实是[0, l]范围,l之后的元素需要删除list.subList(l + 1, list.size()).clear();}return ans == Integer.MAX_VALUE ? -1 : ans;}
}
优化:list.subList(l + 1, list.size()).clear();这一行代码其实是比较耗时的,其实可以用一个变量记录有效值的长度。用二维数组保存子数组的或值和左端点位置
二维数组优化
class Solution {public int minimumSubarrayLength(int[] nums, int k) {// 为什么只需要开32长度的二维数组?// 注意题目中说了nums中的元素最大位int[][] list = new int[32][2]; // list[i][0]表示或值,list[i][1]表示对应的左端点位置int len = 0; // 记录list中的有效值int n = nums.length;int ans = Integer.MAX_VALUE;for (int i = 0; i < n; ++i) {list[len][0] = 0;list[len++] = i;int l = 0, r = 0;for (; r < len; ++r) {int[] cur = list[r];cur[0] |= nums[i];if (cur[0] >= k) {ans = Math.min(ans, i - cur[1] + 1);}if (cur[0] == list[l][0]) {list[l][1] = cur[1]; // 重复值} else {list[++l][0] = cur[0];list[l][1] = cur[1];}}len = l + 1; // 更新有效值的长度}return ans == Integer.MAX_VALUE ? -1 : ans;}
}
为什么只需要开辟32长度的二维数组?
nums[i] <=1 0 9 10^9 109,而 2 29 < 1 0 9 < 2 30 2^{29} < 10^9<2^{30} 229<109<230,假设nums[i] =1 0 9 10^9 109,其二进制位数也就31位。
由于或操作,可以使一位或者多位由0变为1,所以或值最多也就有31种,所以开辟32长度的二维数组,足以保存所有的或值。
相关文章:

【刷题笔记】第三天
两道简单题 文章目录 [2923. 找到冠军 I](https://leetcode.cn/problems/find-champion-i/description/)[3095. 或值至少 K 的最短子数组 I](https://leetcode.cn/problems/shortest-subarray-with-or-at-least-k-i/description/) 2923. 找到冠军 I 方法1: 如果 i …...
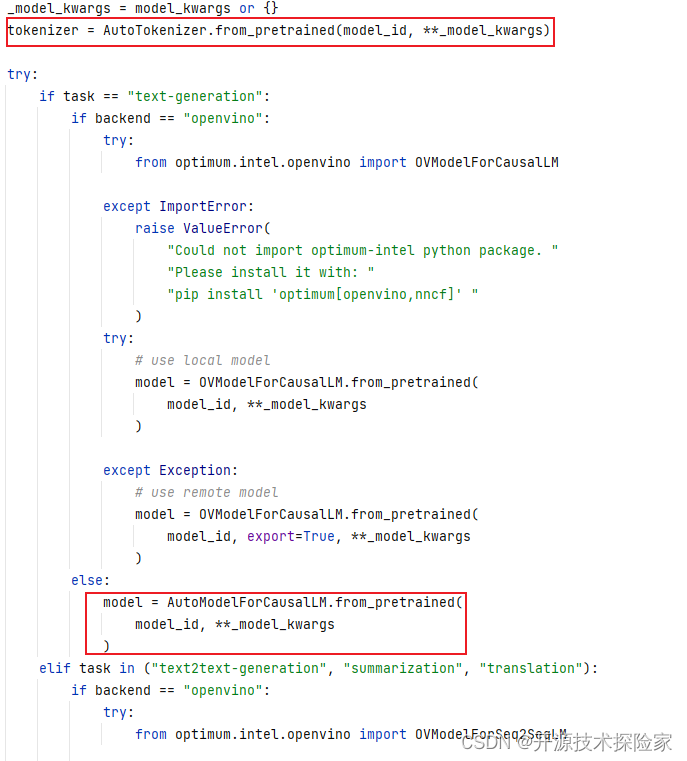
开源模型应用落地-LangChain试炼-CPU调用QWen1.5(一)
一、前言 尽管现在的大语言模型已经非常强大,可以解决许多问题,但在处理复杂情况时,仍然需要进行多个步骤或整合不同的流程才能达到最终的目标。然而,现在可以利用langchain来使得模型的应用变得更加直接和简单。 通过langchain框…...
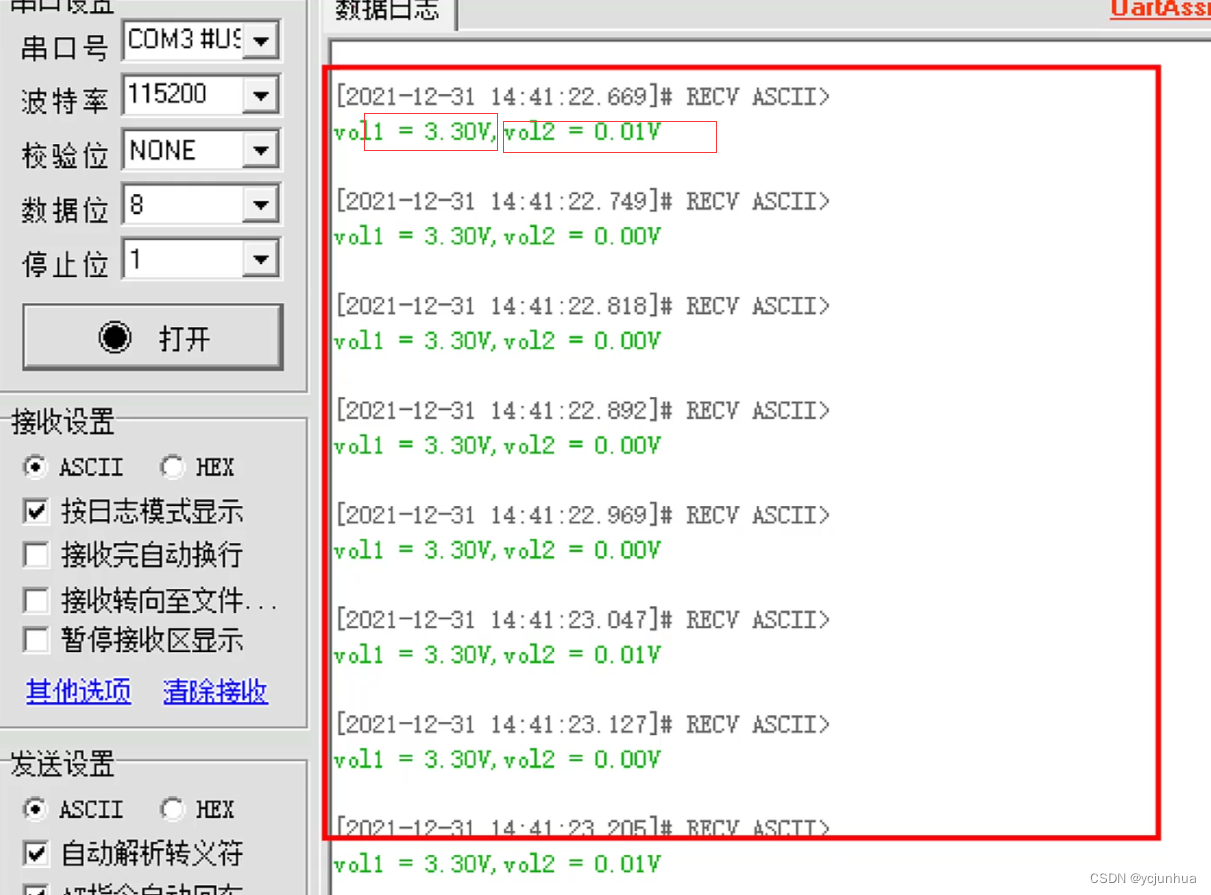
STM32-模数转化器
ADC(Analog-to-Digital Converter) 指模数转换器。是指将连续变化的模拟信号转换 为离散的数字信号的器件。 ADC相关参数说明: 分辨率: 分辨率以二进制(或十进制)数的位数来表示,一般有 8 位、10 位、12 位、16 位…...

算法刷题记录2
4.图 4.1.被围绕的区域 思路:图中只有与边界上联通的O才不算是被X包围。因此本题就是从边界上的O开始递归,找与边界O联通的O,并标记为#(代表已遍历),最后图中剩下的O就是:被X包围的O。图中所有…...

中国代工巨头旗下芯片公司遭网络攻击,千兆字节数据被泄露
近日,中国智能手机代工巨头闻泰科技旗下荷兰芯片制造商Nexperia发布声明,称其遭遇网络攻击,有未经授权的第三方访问了公司的 IT 服务器,目前已向相关部门报告了此次事件,并与网络安全专家合作开启调查。而据相关消息&a…...
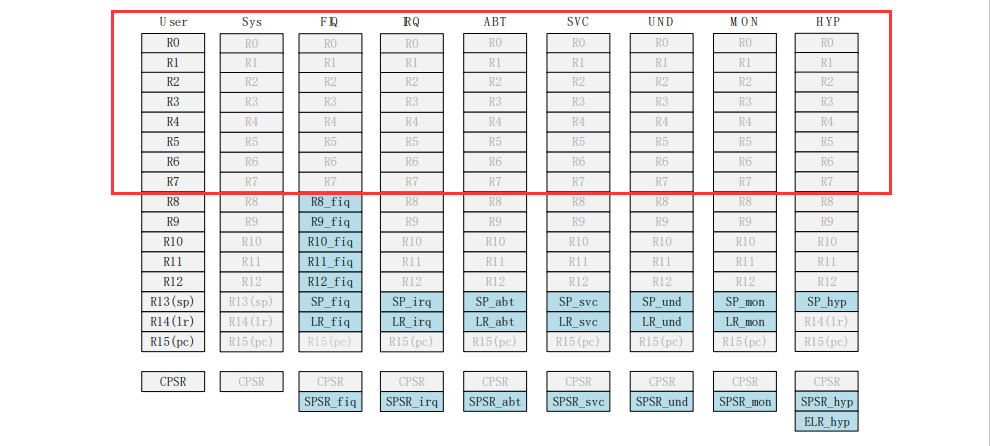
【ARM 裸机】汇编 led 驱动之基本语法
我们要编写的是 ARM 汇编,编译使用的是 gcc 交叉编译器,所以要符合 GNU 语法。 1、汇编指令 汇编由一条条指令构成,ARM 不能直接访问存储器,比如 RAM 中的数据,I.MX6UL 中的寄存器就是 RAM 类型的,我们用…...
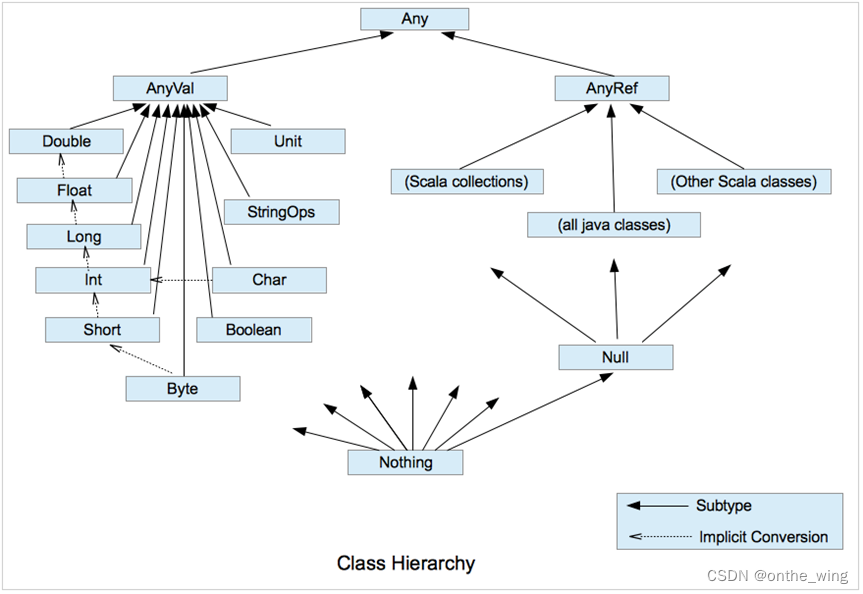
scala---基础核心知识(变量定义,数据类型,流程控制,方法定义,函数定义)
一、什么是scala Scala 是一种多范式的编程语言,其设计初衷是要集成面向对象编程和函数式编程的各种特性。Scala运行于Java平台(Java虚拟机),并兼容现有的Java程序。 二、为什么要学习scala 1、优雅 2、速度快 3、能融合到hado…...
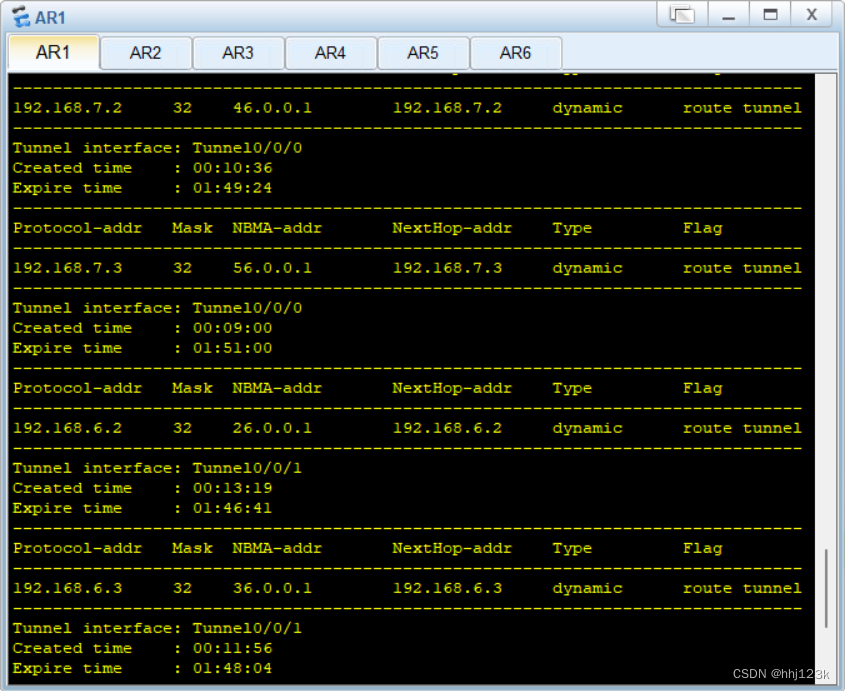
OSPF星型拓扑和MGRE全连
一,拓扑 二,要求 1,R6为ISP只能配置IP地址,R1-R5的环回为私有网段 2,R1/4/5为全连的MGRE结构,R1/2/3为星型的拓扑结构, 3,R1为中心站点所有私有网段可以互相通讯,私有网段…...
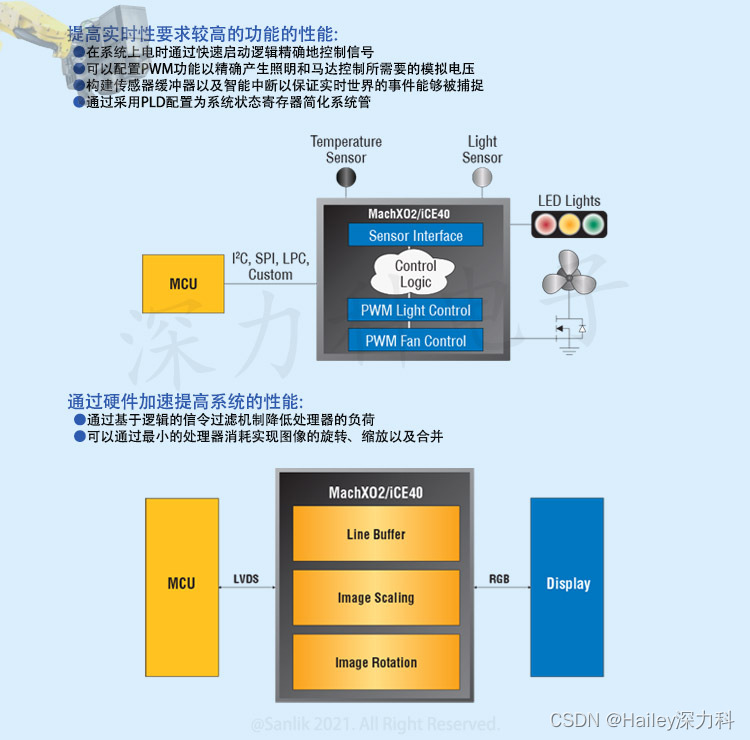
智能时代中的工业应用中前所未有的灵活桥接和I/O扩展功能解决方案MachXO2系列LCMXO2-1200HC-4TG100I FPGA可编程逻辑IC
lattice莱迪斯 MachXO2系列LCMXO2-1200HC-4TG100I超低密度FPGA现场可编程门阵列,适用于低成本的复杂系统控制和视频接口设计开发,满足了通信、计算、工业、消费电子和医疗市场所需的系统控制和接口应用。 瞬时启动,迅速实现控制——启动时间…...
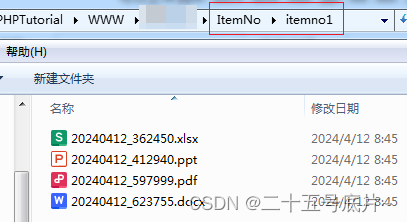
php:实现压缩文件上传、解压、文件更名、压缩包删除功能
效果图 1.上传文件 2.压缩包文件 3.itemno1文件 或 4.上传到系统路径\ItemNo 5.更名后的itemno1文件(命名:当天日期六位随机数) 代码 <form action"<?php echo htmlspecialchars($_SERVER[PHP_SELF], ENT_QUOTES, UTF-8); ?>" methodpost en…...
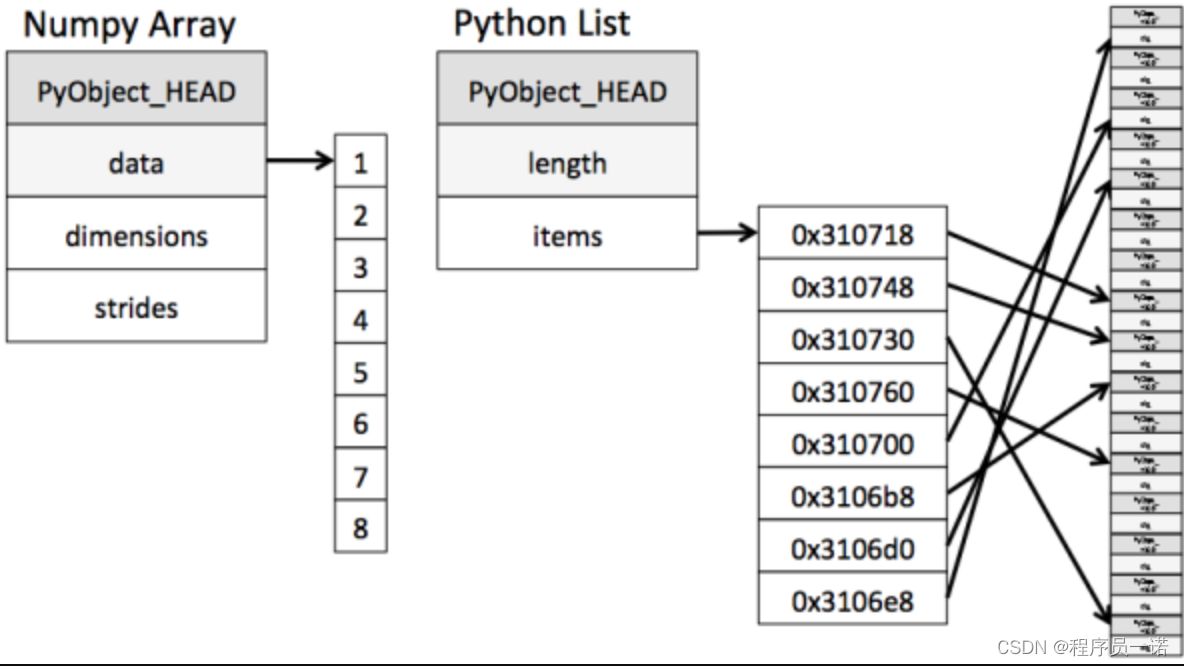
【机器学习】科学库使用第5篇:Matplotlib,学习目标【附代码文档】
机器学习(科学计算库)完整教程(附代码资料)主要内容讲述:机器学习(常用科学计算库的使用)基础定位、目标,机器学习概述定位,目标,学习目标,学习目标,1 人工智能应用场景,2 人工智能小…...
Java面试八股文(JVM篇)(❤❤)
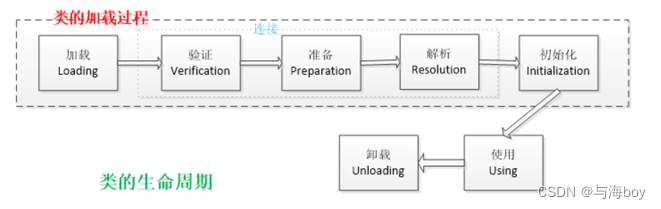
Java面试八股文_JVM篇 1、知识点汇总2、知识点详解:3、说说类加载与卸载11、说说Java对象创建过程12、知道类的生命周期吗?14、如何判断对象可以被回收?17、调优命令有哪些?18、常见调优工具有哪些20、你知道哪些JVM性能调优参数&…...

「51媒体」如何有效进行媒体邀约,提升宣传传播效果?
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 进行有效的媒体邀约,提升宣传传播效果的关键在于策略性和专业性。以下是具体的做法: 明确目标:要确立清晰的品牌推广目标和策略,包括确定目…...

docker初始化进程
docker run --init 是一个 Docker 命令的选项,用于在容器中运行一个初始化进程(通常是 tini)。这个初始化进程负责处理一些 Unix 信号(如 SIGTERM 和 SIGCHLD),并确保容器中的进程能够正确地被管理和清理。…...

基于快照行情的股票/基金 1分钟 K 线合成指南
1. 概述 由于不同交易所不同资产的交易规则是有差异的,导致不同交易所基于快照行情或逐笔成交合成不同资产1分钟 K 线的计算方法是不同的。 本教程旨在提高 DolphinDB 在具体业务场景下的落地效率,降低 DolphinDB 在实际业务使用中的开发难度。 本教程…...

新质生产力崛起:精益化能力助力企业转型升级
在智能制造、物联网、大数据、大模型、AI风起云涌的时代背景下,一个崭新的概念——“新质生产力”逐渐进入了人们的视野。这一热词不仅成为今年两会的讨论焦点,更代表了企业、国家乃至社会未来发展的核心动能。那么,什么是新质生产力…...

开发了一个在线客服系统
开发了一个在线客服系统 作为程序员,我一直在寻找能够提高工作效率和用户体验的方法。最近,我成功开发了一个在线客服系统,这个系统旨在帮助企业更高效地管理客户咨询和服务流程。 技术栈 我选择了以下的技术栈来构建这个系统:…...
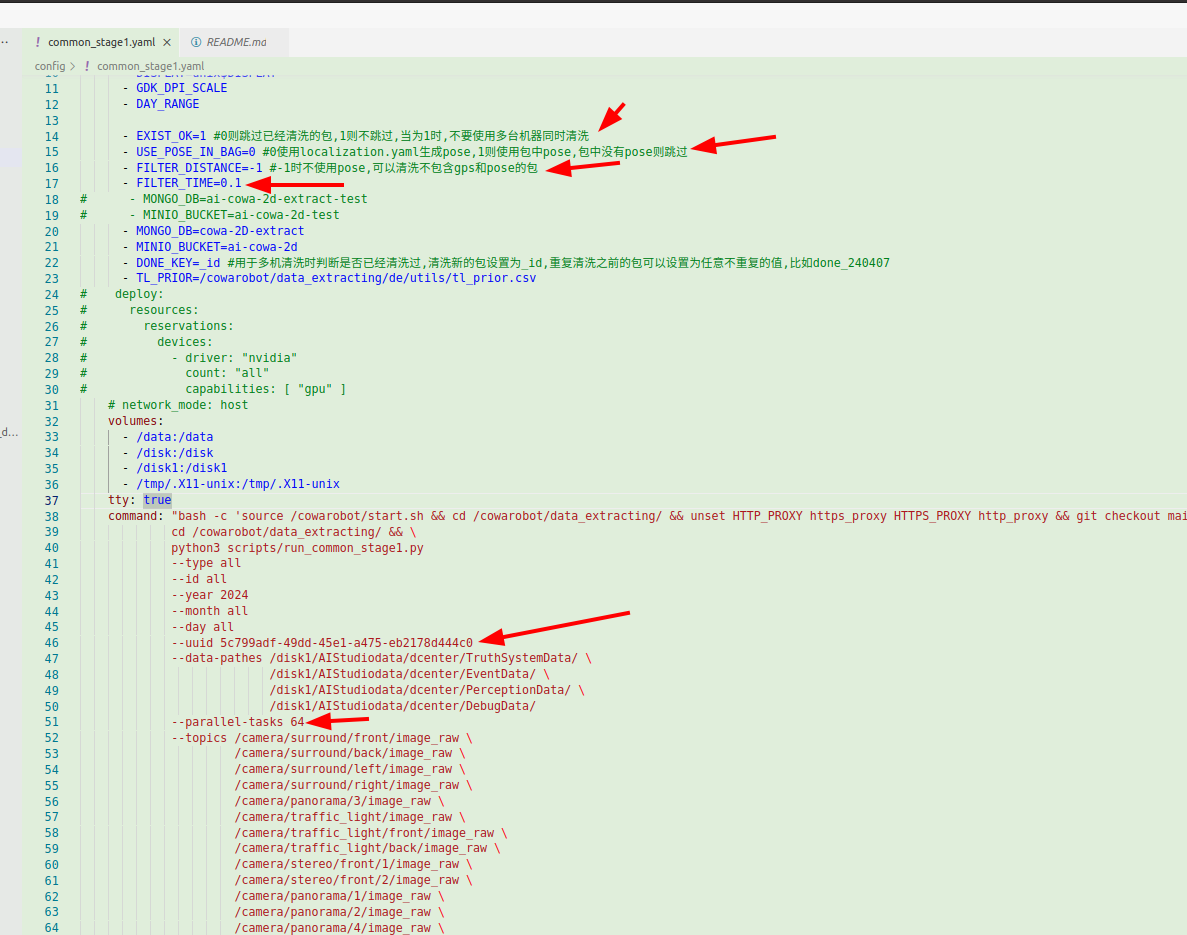
cowa新的数据筛选代码
cowa新的数据筛选代码 代码地址: https://git.cowarobot.com/lhb/data_extracting 一阶段筛选 修改配置文件 config/common_stage.yamlversion: 3 services:de:image: harbor.cowarobot.cn/lhb/data:crpilot2.5-torch2.2environment:- CRPILOT_INSTALL_VERSIONx86…...

项目篇 | 图书管理系统 | 管理员模块 | 图书管理 | 删除
项目篇 | 图书管理系统 | 管理员模块 | 图书管理 | 删除 概述 图书管理页通过列表展示所有图书的相关信息,集成了搜索、添加、删除、修改的功能。 函数简介 // admin.h void delBook(); // 删除图书 void openDelBookMessage(); // 打开删除图书弹框 void closeDelBookMessa…...

自己动手封装axios通用方法并上传至私有npm仓库:详细步骤与实现指南
文章目录 一、构建方法1、api/request.js2、api/requestHandler.js3、api/index.js 二、测试方法1、api/axios.js2、main.js3、app.vue4、vue.config.js5、index.html 三、打包1、配置package.json2、生成库包3、配置发布信息4、发布 四、使用1、安装2、使用 五、维护1、维护和…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
