24.5.5(离散化+树状数组,线段树)
星期一:
dp题单 背包 第四题 混可乐 cf传送门

思路:条件可演化为每种可乐值为 ai-n,选最少的可乐使总和为0(具体可看官方题解
到这会发现背包并不适合了,其实这是道bfs伪装的背包,和牛客周赛39 D很像 牛客传送门
代码如下:
ll n;
int k;
int dis[2020];
void solve(){cin >> n >> k;memset(dis,-1,sizeof dis);queue<int>qu;map<int,int>mp;for(int i=1;i<=k;i++){int x; cin >>x;x=x-n+1000;if(dis[x]==-1) dis[x]=1,qu.push(x),mp[x]=1;}while(!qu.empty()){int t=qu.front(); qu.pop();
// for(int i=0;i<=2000;i++){
// if(i+t-1000<0 || i+t-1000>2000) continue;
// if(dis[t+i-1000]!=-1 || dis[i]!=1) continue;
// dis[t+i-1000]=dis[t]+1;
// qu.push(t+i-1000);
// }for(auto [x,y]:mp){if(x+t-1000<0 || x+t-1000>2000) continue; //x和t都经过了一次偏移if(dis[x+t-1000]!=-1) continue; //所以加起来后需要减一次偏移量dis[x+t-1000]=dis[t]+1; //新到达的点qu.push(x+t-1000);}}if(dis[1000]==-1) cout << "-1\n";else cout << dis[1000] << "\n";
}晚cf,C是dp没出
星期二:
cf edu 165 补C cf传送门

思路:贪心证伪后用dp考虑,状态设计及转移大致如下

这里提一点卡我很久很久的地方,第一重循环 i 需要从0开始枚举
因为状态转移并不是由 i之前推到 i,而是从 i往后面推, i从1开始的话,有些状态无法转移出来,这点在以后也需要注意
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int k;
int a[N];
ll dp[N][11];
void solve(){cin >> n >> k;for(int i=1;i<=n;i++){cin >> a[i];dp[i][0]=dp[i-1][0]+a[i];for(int j=1;j<=k;j++) dp[i][j]=1e18;}for(int i=0;i<=n;i++){int mi=a[i+1];for(int j=0;j<=k;j++){mi=min(a[i+j+1],mi);for(int o=0;o+j<=k;o++){dp[i+j+1][o+j]=min(dp[i][o]+1ll*mi*(j+1),dp[i+j+1][o+j]);}}}cout << dp[n][k] << "\n";
}晚cf round942 div2,最后十分钟出C,又被permutation拿下了
星期三:
上午vp牛客周赛28
E 牛客传送门
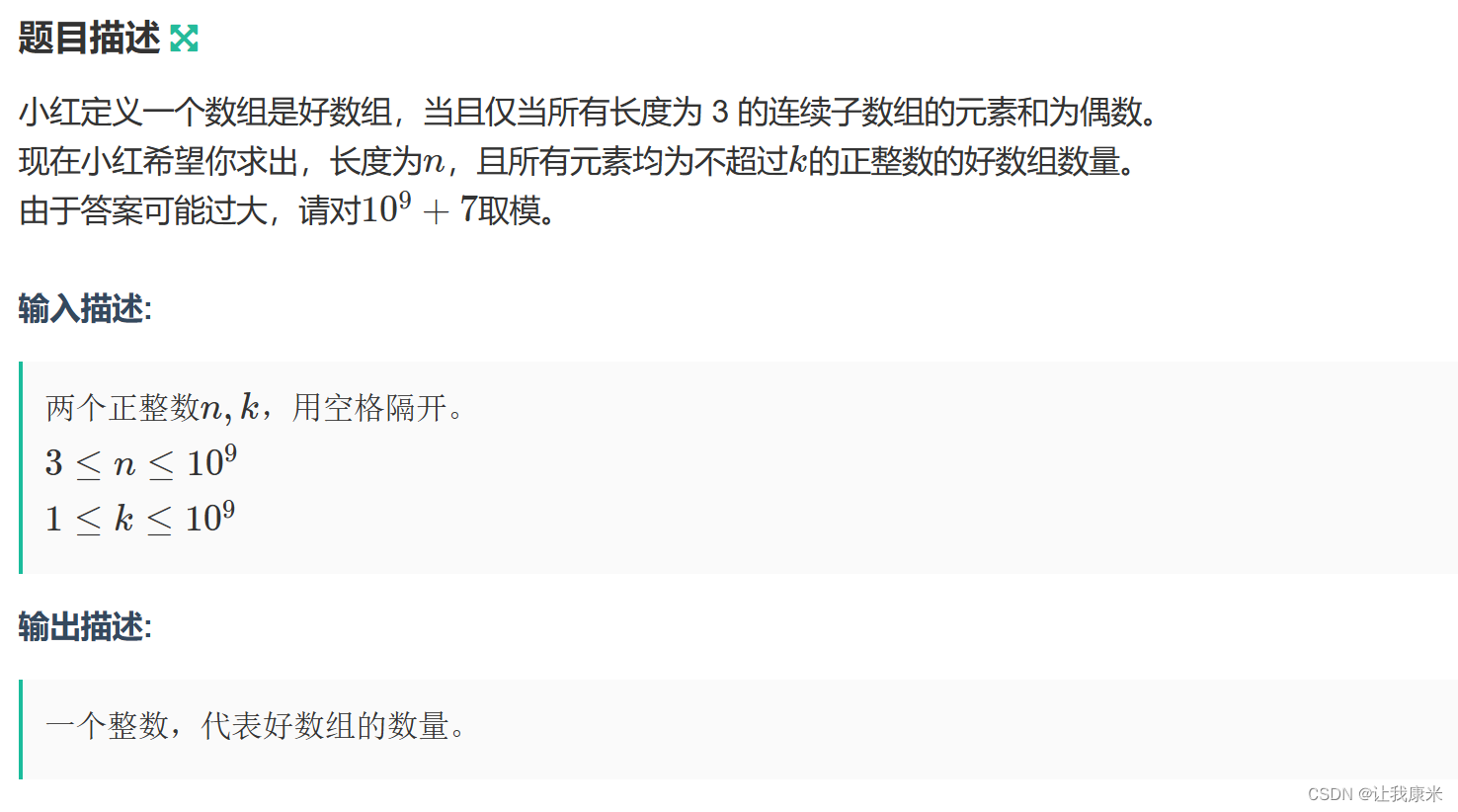
思路:三个连续数的和为偶数,组合形式有限,分别为偶偶偶,偶奇奇,奇偶奇,奇奇偶,数组最先三个数的奇偶性确定后,整个数组的每个数的奇偶性都确定了
算出k以内的数能选的奇数和偶数个数,n个位置中奇数和偶数各有多少个,乘法原理和快速幂计算
代码如下:
const int mod=1e9+7;
ll n;
ll k;
ll qpow(int a,int n){if(n==0) return 1;if(n==1) return a;ll s=qpow(a,n/2);s=s*s%mod;if(n&1) s=s*a%mod;return s;
}
void solve(){cin >> n >> k;int num0=0,num1=0;num0=k/2,num1=k/2+(k&1);ll ans=qpow(num0,n); //全偶int n0=n/3,n1=n/3*2;if(n%3==0) ans+=3*qpow(num1,n1)*qpow(num0,n0)%mod,ans%=mod;if(n%3==1)ans+=2*qpow(num1,n1+1)*qpow(num0,n0)%mod,ans+=qpow(num1,n1)*qpow(num0,n0+1),ans%=mod;if(n%3==2)ans+=2*qpow(num1,n1+1)*qpow(num0,n0+1)%mod,ans+=qpow(num1,n1+2)*qpow(num0,n0),ans%=mod;cout << ans;
}下午牛客五一 1,很难,看情况补题
周赛28 F题离散化+树状数组,先复习下树状数组,刚好趁五一假期学点数据结构
洛谷树状数组板子题其一(单点修改,区间查询 洛谷传送门

代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll m;
ll a[N];
ll t[N];
int lowbit(int x){return x&-x;}
void ad(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) t[i]+=v;
}
ll ask(int x){ll res=0;for(int i=x;i;i-=lowbit(i)) res+=t[i];return res;
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++){cin >> a[i];ad(i,a[i]); //nlogn构造树状数组}while(m--){int op,x,y; cin >> op >> x >> y;if(op==1) ad(x,y);else cout << ask(y)-ask(x-1) << "\n";}
}树状数组板子题其二(区间修改,单点查询 洛谷传送门
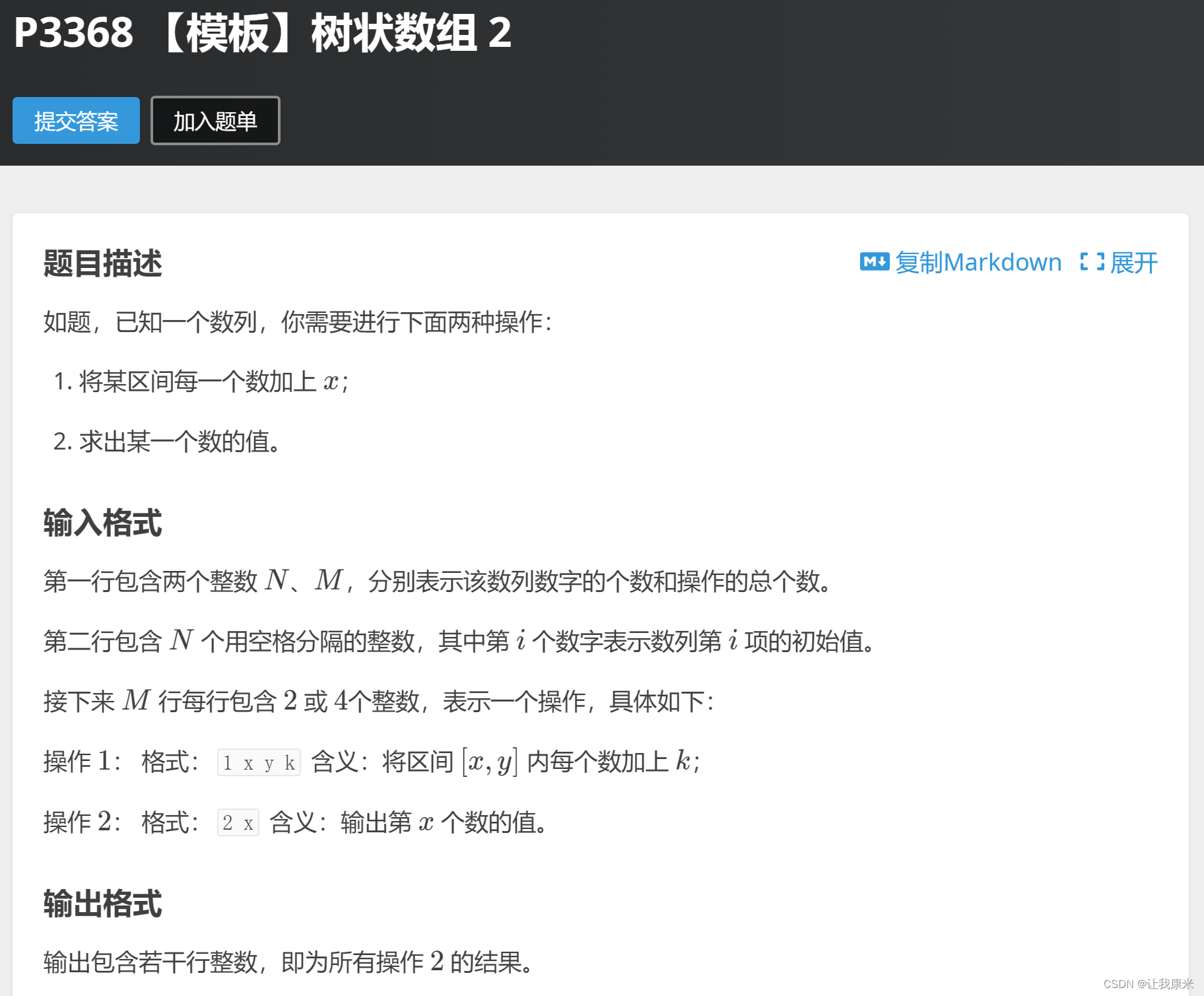
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll m;
ll a[N];
ll t[N];
int lowbit(int x){return x&-x;}
void ad(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) t[i]+=v;
}
ll ask(int x){ll res=0;for(int i=x;i;i-=lowbit(i)) res+=t[i];return res;
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++) cin >> a[i];while(m--){int op,x; cin >> op >> x;if(op==1){int y,k; cin >> y >> k;ad(x,k); ad(y+1,-k); //差分思想,x到y这段区间加上了k}else cout << a[x]+ask(x) << "\n"; //t数组维护的是修改值}
}星期四:
补牛客周赛28 F 牛客传送门

思路:因为前缀和不再有单调性,所以easy版本二分和双指针的做法失效,用离散化+树状数组
区间元素和大于等于k,即 a【l-1】<= a【r】- k,我们可以枚举右端点,然后查询有多少个左端点小于等于这个值,枚举后将此右端点加入左端点的集合,这里用权值树状数组来实现
权值树状数组,单点修改,区间查询,修改的意义是值为x的数多了1,查询的意义即为<= x的值个数,类似于用树状数组维护桶数组
不过由于值的范围能到达1e14,需要离散化处理,即按照原值的大小关系映射为紧密连续的值,这里需要用到的值不仅有 a【i】,还有 a【i】- k 用于查询,所以离散化后数据范围最多 2e5
最后一个需要注意的点是,add函数的 i <= n,需改为 i <= 离散化后映射的最大值,因为这才是 离散化后权值树的最大下标
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll a[N],k;
ll t[N],cnt;
map<ll,int>to;
int lowbit(int x){return x&-x;}
void add(int x,int v){for(int i=x;i<=cnt;i+=lowbit(i)) t[i]+=v; //注意下标并不为 n !!!
}
ll ask(int x){ll res=0;for(int i=x;i;i-=lowbit(i)) res+=t[i];return res;
}
void solve(){cin >> n >> k;for(int i=1;i<=n;i++){cin >> a[i];a[i]+=a[i-1];to[a[i]]=1,to[a[i]-k]=1;}to[0]=1;for(auto &[x,y]:to) y=++cnt; //离散化处理ll ans=0;add(to[0],1); //因为查询的是a[l-1],a[0]=0的值先加上for(int i=1;i<=n;i++){ans+=ask(to[a[i]-k]); //查询add(to[a[i]],1); //权值+1}cout << ans;
}牛客五一集训 1 补B(斐波那契字符串 牛客传送门

思路:n 比较小,可以递归求解,f 数组储存此字符串的长度
代码如下:
ll n;
ll f[550];
const ll MA=1e12+10;
inline char fnd(int n,ll k){if(n==1) return "COFFEE"[k-1];if(n==2) return "CHICKEN"[k-1];if(k<=f[n-2]) return fnd(n-2,k); //此字符属于第i-2个字符串else return fnd(n-1,k-f[n-2]); //否则属于第i-1个
}
void solve(){f[1]=6,f[2]=7;for(int i=3;i<=510;i++) f[i]=min(MA,f[i-2]+f[i-1]);int t; cin >> t;while(t--){ll k; cin >> n >> k;for(ll i=k;i<min(k+10,f[n]+1);i++) cout << fnd(n,i);//i注意开llcout << "\n";}
}其他题都不是很好补,先放会
准备补牛客寒假集训营2的两道线段树题,过程可能会比较漫长,期望在4号内完成
晚cf round 943,B题翻车,题数4题
星期五:
先敲个线段树板子,复习下
代码如下:(区间修改,区间查询
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
#define lc p<<1
#define rc p<<1|1
int m;
struct nod{ll l,r,sum,add; //左端点,右端点,区间总和,懒标记
}t[N]; //要开原数组 4倍大小
ll a[N];
void pushup(int p){ //向上更新t[p].sum=t[lc].sum+t[rc].sum;
}
void pushdn(int p){ //向下更新if(!t[p].add) return ;t[lc].sum+=(t[lc].r-t[lc].l+1)*t[p].add;t[rc].sum+=(t[rc].r-t[rc].l+1)*t[p].add;t[lc].add+=t[p].add;t[rc].add+=t[p].add;t[p].add=0;
}
void bd(int p,int l,int r){t[p]={l,r,a[l],0};if(l==r) return ; //叶子节点int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);
}
ll ask(int p,int x,int y){ //区间查询if(x<=t[p].l && y>=t[p].r) return t[p].sum; //被查询区间完全覆盖,则直接返回sumll sum=0;int m=t[p].l+t[p].r>>1;pushdn(p); //向下查前先向下更新if(x<=m) sum+=ask(lc,x,y); //有覆盖到左子节点if(y>m) sum+=ask(rc,x,y); //有覆盖到右子节点return sum;
}
void updt(int p,int x,int y,int k){if(x<=t[p].l && y>=t[p].r){t[p].sum+=(t[p].r-t[p].l+1)*k;t[p].add+=k;return ; //打上懒标记,直接返回}int m=t[p].l+t[p].r>>1;pushdn(p); //记得先向下更新if(x<=m) updt(lc,x,y,k);if(y>m) updt(rc,x,y,k);pushup(p); //再向上更新
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++) cin >> a[i];bd(1,1,n);while(m--){int op,x,y; cin >> op >> x >> y;if(op==1){int k; cin >> k;updt(1,x,y,k);}else cout << ask(1,x,y) << "\n";}
}补牛客寒假营2 G 牛客传送门

思路:线段树维护两个信息,区间最大值( suma【i】- 2*a【i】) 和区间和,但区间和不需要区间修改,区间最大值需要(a【x】变化会使 x到n的前缀和改变),所以一个懒标记给区间最大值用就行
官方题解:【题解】2024牛客寒假算法基础集训营2_牛客网 (nowcoder.com)
还有一个我de了半个下午,需要注意的一点是,求区间信息时,一定要确保 l <= r !!!
代码如下:(魔改的比较随意
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
#define lc p<<1
#define rc p<<1|1
struct nod{ll l,r,sum,add,ma;
}t[N];
ll a[N],suma[N];
void pushup(int p){t[p].sum=t[lc].sum+t[rc].sum;t[p].ma=max(t[lc].ma,t[rc].ma);
}
void pushdn(int p){if(!t[p].add) return ;t[lc].ma+=t[p].add; //懒标记只需给最大值用t[rc].ma+=t[p].add;t[lc].add+=t[p].add;t[rc].add+=t[p].add;t[p].add=0;
}
void bd(int p,int l,int r){t[p]={l,r,a[l],0,suma[l]-2*a[l]};if(l==r) return ;int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);
}
ll ask(int p,int x,int y,int op){ //op为1求区间和,为2求区间最大值if(x<=t[p].l && y>=t[p].r){if(op==1) return t[p].sum;else return t[p].ma;}ll res=0;int m=t[p].l+t[p].r>>1;pushdn(p); //记得向下更新if(op==1){res=0;if(x<=m) res+=ask(lc,x,y,1);if(y>m) res+=ask(rc,x,y,1);}else{res=-1e18;if(x<=m) res=max(ask(lc,x,y,2),res);if(y>m) res=max(ask(rc,x,y,2),res);}return res;
}
void updt(int p,int x,int y,int k,int op){ //op为1改区间最大值,为2改区间和(单点修改)if(x<=t[p].l && y>=t[p].r){if(op==1){t[p].ma+=k;t[p].add+=k;}else t[p].sum=k;return ;}int m=t[p].l+t[p].r>>1;pushdn(p);if(x<=m) updt(lc,x,y,k,op);if(y>m) updt(rc,x,y,k,op);pushup(p);
}
void solve(){int q; cin >> n >> q;for(int i=1;i<=n;i++){cin >> a[i];suma[i]=suma[i-1]+a[i];}bd(1,1,n);while(q--){int op,x,y; cin >> op >> x >> y;if(op==1){updt(1,x,x,2*a[x]-2*y,1); //将 sum[i]-2*a[x]改为 sum[i]-2*yupdt(1,x,n,y-a[x],1); //x-n的区间最大值全减a[x]加y (前缀和改变)updt(1,x,x,y,2);a[x]=y;}else{
// cout << ask(1,x+1,y,2)-ask(1,1,x-1,1) << "\n";ll res=ask(1,x+1,y,2);if(x-1>=1) res-=ask(1,1,x-1,1); // 特判x-1!!!cout << res << "\n";}}
}星期六:
线段树维护区间最大子段和板子题 洛谷传送门
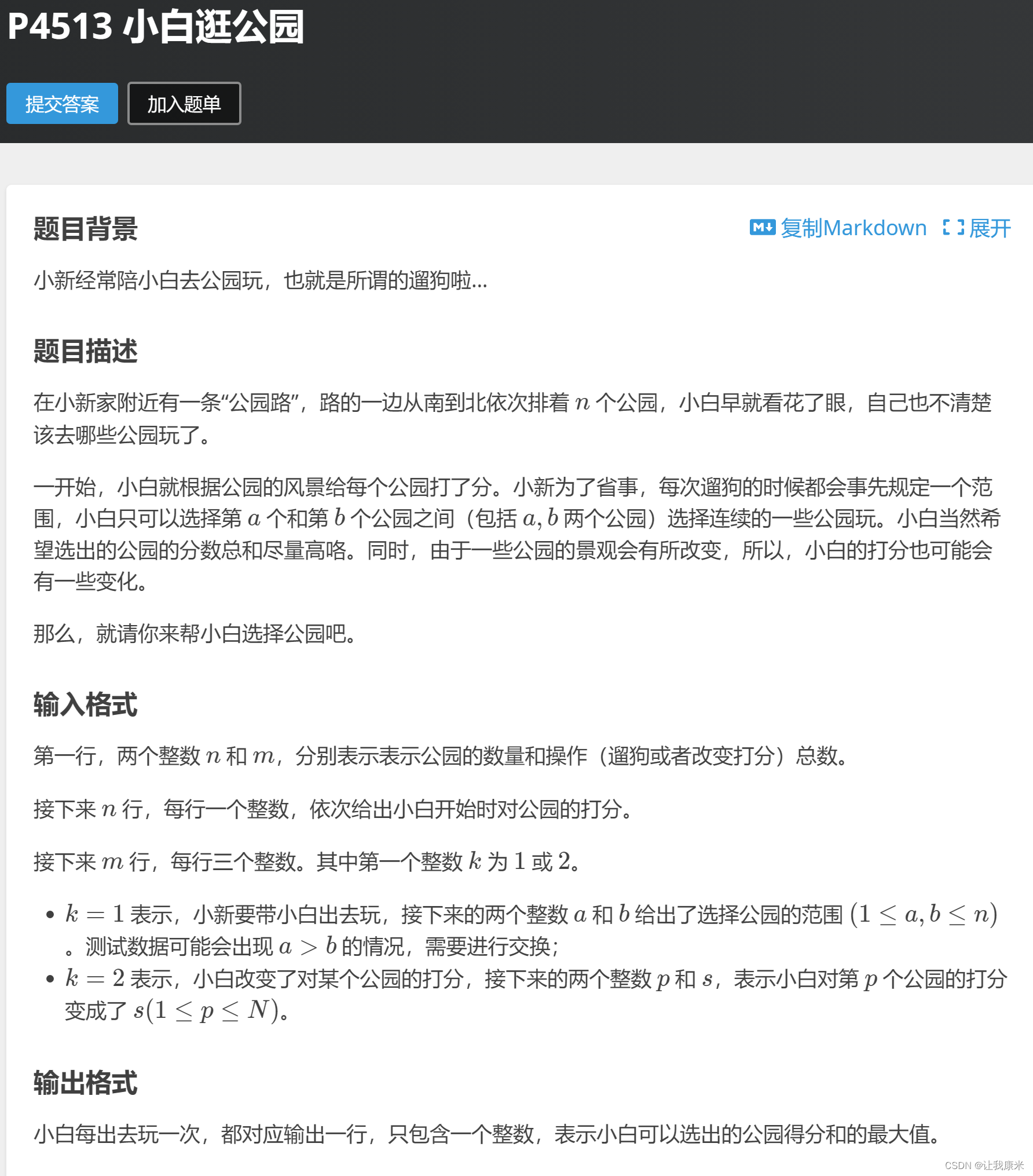
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
struct seg_Tree{#define lc p<<1#define rc p<<1|1struct nod{int l,r;ll sum,maxl,maxr,ma;}t[N];int ql,qr; //查询区间nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.sum=a.sum+b.sum;;res.maxl=max(a.maxl,a.sum+b.maxl);res.maxr=max(b.maxr,a.maxr+b.sum);res.ma=max({a.maxr+b.maxl,a.ma,b.ma});return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);} //向上更新void bd(int p,int l,int r){ //bd里处理输入if(l==r){t[p]={l,r,0,-0x3f3f3f3f,-0x3f3f3f3f,-0x3f3f3f3f};cin >> t[p].sum;t[p].maxl=t[p].maxr=t[p].ma=t[p].sum;return ;}int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p,int v){if(ql<=t[p].l && qr>=t[p].r){t[p].sum=t[p].maxl=t[p].maxr=t[p].ma=v; //叶子节点的所有信息都要改return ;}int m=t[p].l+t[p].r>>1;if(ql<=m) update(lc,v);if(qr>m) update(rc,v);pushup(p); //向上更新}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;if(ql>m) return query(rc);if(qr<=m) return query(lc);return merge(query(lc),query(rc));}void updt(int l,int r,int v){ql=l;qr=r;
// qop=op;update(1,v);}ll ask(int l,int r){ql=l,qr=r;return query(1).ma;}#undef lc#undef rc
}tr;
void solve(){int m; cin >> n >> m;tr.bd(1,1,n);while(m--){int k,a,b; cin >> k >> a >> b;if(k==1){if(a>b) swap(a,b);cout << tr.ask(a,b) << "\n";}else tr.updt(a,a,b);}
}周日:
川大校赛初赛,输
补牛客寒假营2 H 牛客传送门
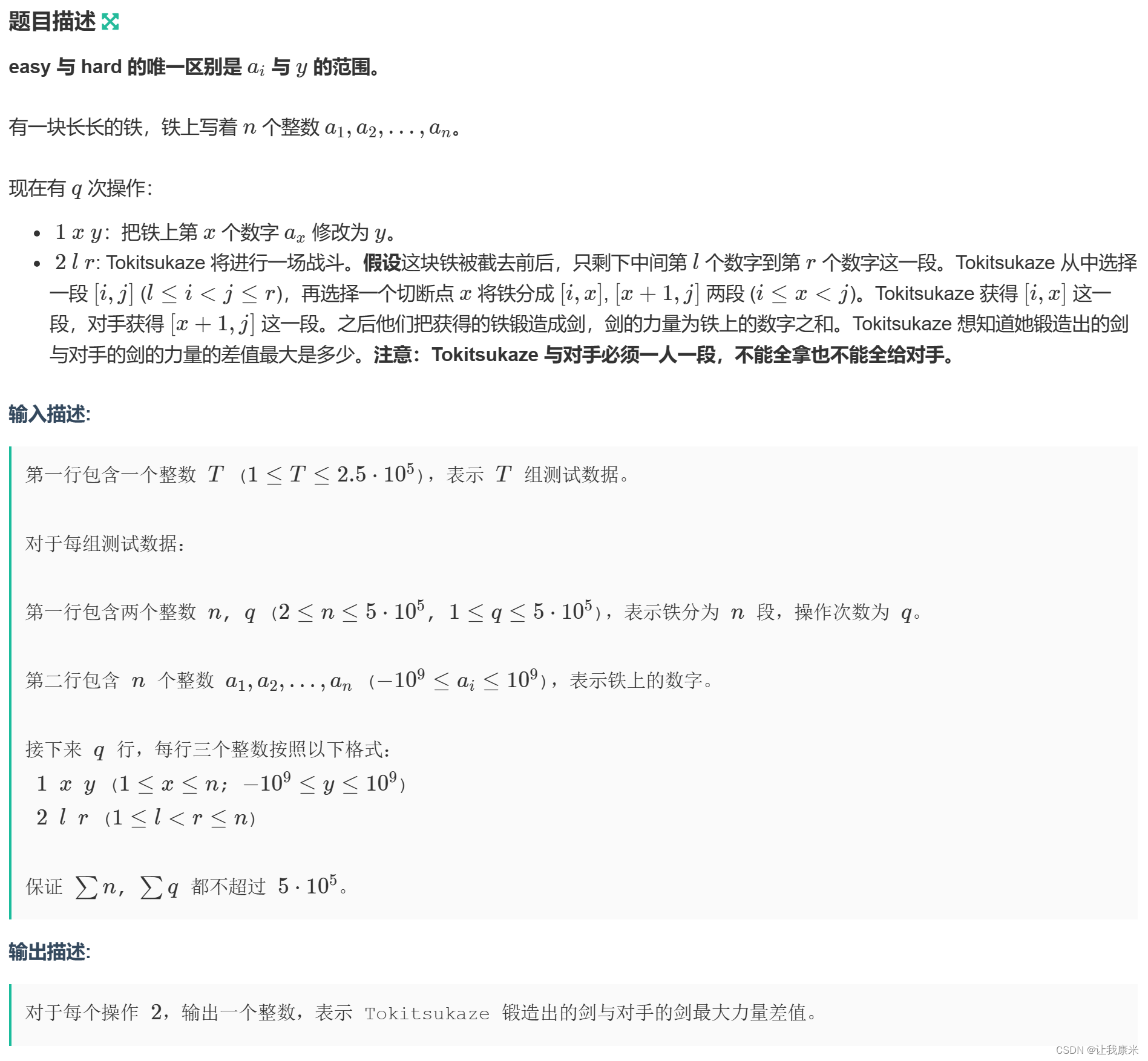
思路:easy版本的贪心失效,在线段树维护区间最大子段和的基础上修改一下
官方题解很详细:【题解】2024牛客寒假算法基础集训营2_牛客网 (nowcoder.com)
代码如下:
const int N=2e6+10,M=210;
const ll INF=0x3f3f3f3f3f3f3f3f; //必须得开ll
const int mod=1e9+7;
ll n;
struct seg_Tree{#define lc p<<1#define rc p<<1|1struct nod{int l,r;ll sum,maxr,minl,ansl,ansr,segans,ans;}t[N];int ql,qr,qop,a[N];nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.sum=a.sum+b.sum;res.maxr=max(b.maxr,a.maxr+b.sum);res.minl=min(a.minl,a.sum+b.minl);res.ansl=max({a.ansl,a.sum+b.ansl,a.sum-b.minl,a.segans-b.minl});res.ansr=max({b.ansr,a.ansr-b.sum,a.maxr-b.sum,a.maxr+b.segans});res.segans=max({a.sum-b.sum,a.segans-b.sum,a.sum+b.segans});res.ans=max({a.ans,b.ans,a.maxr-b.minl,a.ansr-b.minl,a.maxr+b.ansl});return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);}void bd(int p,int l,int r){t[p]={l,r,a[l],-INF,INF,-INF,-INF,-INF,-INF};if(l==r){t[p].maxr=t[p].minl=t[p].sum;return ;}int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p,int v){if(ql<=t[p].l && qr>=t[p].r){t[p].maxr=t[p].minl=t[p].sum=v;return ;}int m=t[p].l+t[p].r>>1;if(ql<=m) update(lc,v);if(qr>m) update(rc,v);pushup(p);}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;if(ql>m) return query(rc);if(qr<=m) return query(lc);return merge(query(lc),query(rc));}void updt(int l,int r,int v){ql=l;qr=r;
// qop=op;update(1,v);}ll ask(int l,int r){ql=l,qr=r;return query(1).ans;}#undef lc#undef rc
}tr;
void solve(){int q; cin >> n >> q;for(int i=1;i<=n;i++) cin >> tr.a[i];tr.bd(1,1,n);while(q--){int op,x,y; cin >> op >> x >> y;if(op==1) tr.updt(x,x,y);else cout << tr.ask(x,y) << "\n";}
}相关文章:

24.5.5(离散化+树状数组,线段树)
星期一: dp题单 背包 第四题 混可乐 cf传送门 思路:条件可演化为每种可乐值为 ai-n,选最少的可乐使总和为0(具体可看官方题解 到这会发现背包并不适合了,其实这是道bfs伪装的背包…...

C语言 | Leetcode C语言题解之第69题x的平方根
题目: 题解: int mySqrt(int x) {long int i 0;for(i0;;i){long int a i*i;long int b (i1)*(i1);if(a < x&&b > x){break;}}return i; }...

静态分配IP,解决本地连接不上Linux虚拟机的问题
在Window环境下,使用远程终端工具连接不了VMware搭建的Linux虚拟机(CentOS 7),并且在命令行ping不通该Linux虚拟机的IP地址。下面通过配置网关解决本地与Linux虚拟机连接问题: 1 查看虚拟机网关地址 在VMware虚拟机上…...

每日JAVA高级面试题
Java 高级面试问题及答案 以下是几个Java高级面试中可能会问到的问题,包括问题、答案以及一些探讨过程。 问题1: 请解释Java中的多线程以及线程池的使用场景和优势 答案: Java中的多线程允许程序执行多个任务,从而提高应用程序的响应速度和…...
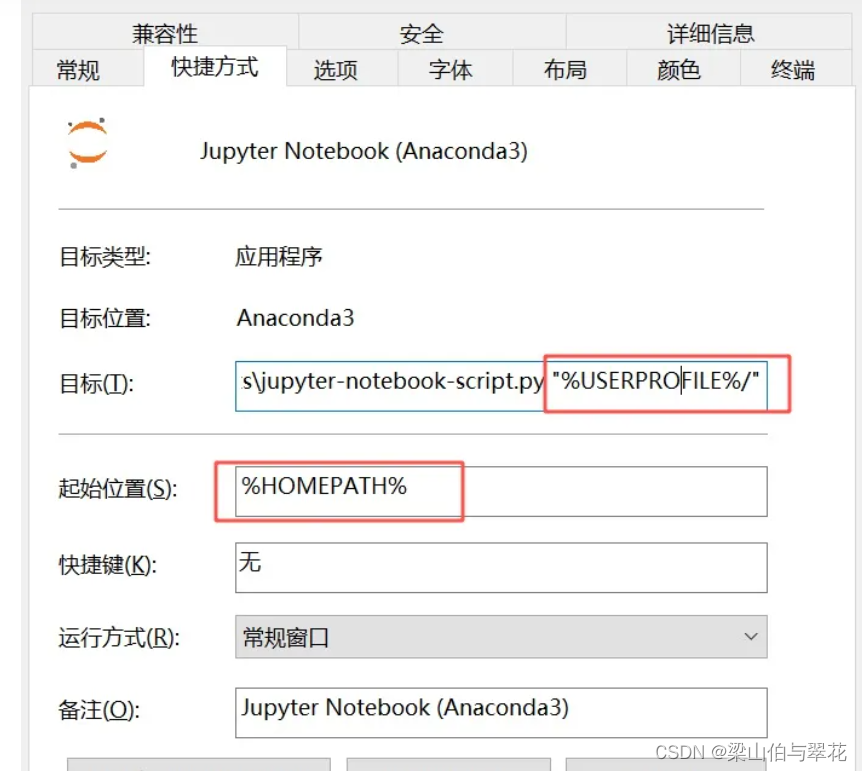
修改JupyterNotebook文件存储位置
Jupyter Notebook 1、通过AnaConda安装Jupyter Notebok 2、在开始菜单里找到并打开Anaconda Prompt,输入如下命令,然后执行。 jupyter notebook --generate-config4、打开以下文件 找到 C:/Userzh/.../.jupyter 打开 jupyter_notebook_config.py 取消…...

python Flask路由系统如何影响应用性能的一些关键点
Flask的路由系统对应用性能的影响主要体现在路由匹配和分发请求的效率上。以下是关于Flask路由系统如何影响应用性能的一些关键点: 路由匹配方式:Flask支持精准匹配和模糊匹配两种方式。精准匹配是指URL中的路径和定义的路由规则完全匹配,而…...
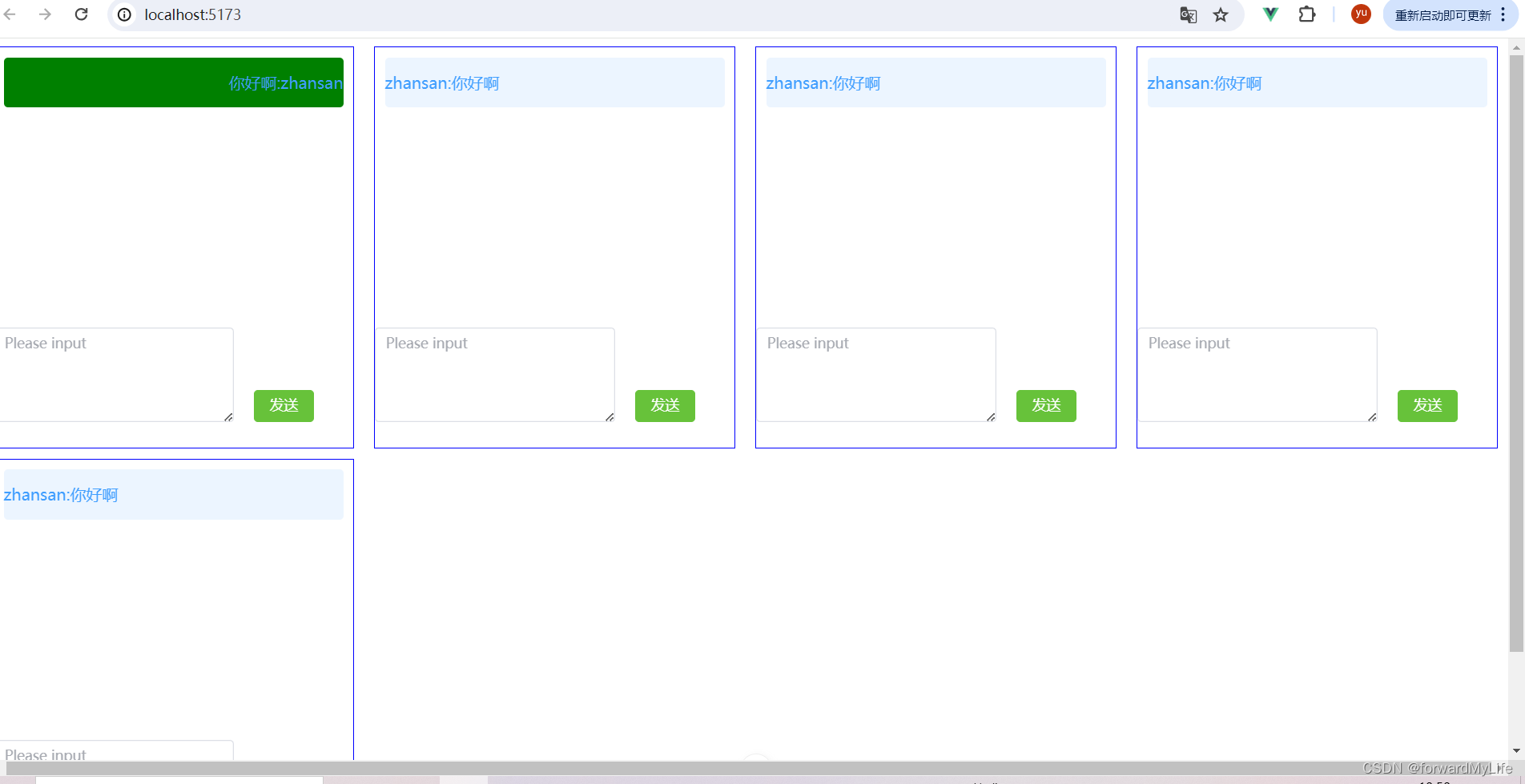
nodejs的ws+vue3编写聊天室的demo
nodejs编写ws服务是非常简单高效的,nodejs有众多的实现ws的库,如ws,SocketIO等,nodejs的事件线程是单线程的,所以不要在事件线程内做阻塞性的操作,耗时的操作交给工作线程或者子进程操作。 我使用nodejsvue3实现了写了…...
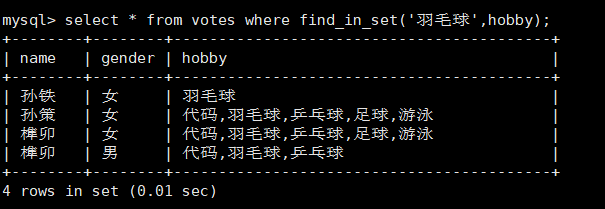
《MySQL数据类型》
文章目录 一、理解数据本身就是一种约束1.tinyint类型和 tinyint unsigned类型2.其他的int类型 二、bit类型三、float类型1.signed版本注意2.unsigned版本 四、decimal类型float 和 decimal 总结五、char类型(固定长度)六、varchar类型(可变长…...
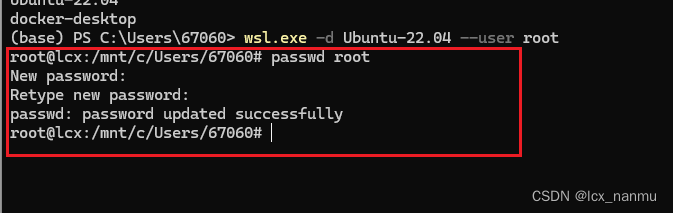
解决windows中的WSL Ubuntu子系统忘记root密码和用户密码问题
1、以管理员身份运行PowerShell 2、在powershell中执行wsl.exe --user root wsl.exe --user root如果出现了上面的报错,则需要运行步骤3、4,然后在执行步骤5改密码,如果没有出错,请直接跳到第5步改密码操作!ÿ…...

数据分析——业务指标分析
业务指标分析 前言一、业务指标分析的定义二、业务问题构建问题构建的要求 三、业务问题的识别在识别问题的阶段对于企业内部收益者的补充 四、竞争者分析竞争者分析的内容竞争者分析目的案例 五、市场机会识别好的市场机会必须满足的条件市场机会案例 六、风险控制数据分析师常…...

给c++小白的教程9:循环
老师给比纳瑞出了一道题。 给出 𝑛 和 𝑛 个整数 𝑎𝑖,求这 𝑛 个整数中最小值是什么。 由题意得,此题无论是顺序结构或是选择结构都连输入也解决不了。 这时候,我们就要用上循环…...

SLAIM:一个实时的RGB-D NeRF-SLAM系统
SLAIM:一个实时的RGB-D NeRF-SLAM系统与现有的NeRF-SLAM系统相比,我们的方法在跟踪性能上始终表现出更强的竞争力。我们的方法采用体积密度表示,并引入了一种新的KL正则化器在射线终止分布上,将场景几何限制为空隙空间和不透明表面…...
PWN入门之Stack Overflow
Stack Overflow是一种程序的运行时(runtime)错误,中文翻译过来叫做“栈溢出”。栈溢出原理是指程序向栈中的某个变量中写入的字节数超过了这个变量本身所申请的字节数,导致与其相邻的栈中的变量值被改变。 在本篇文章中ÿ…...
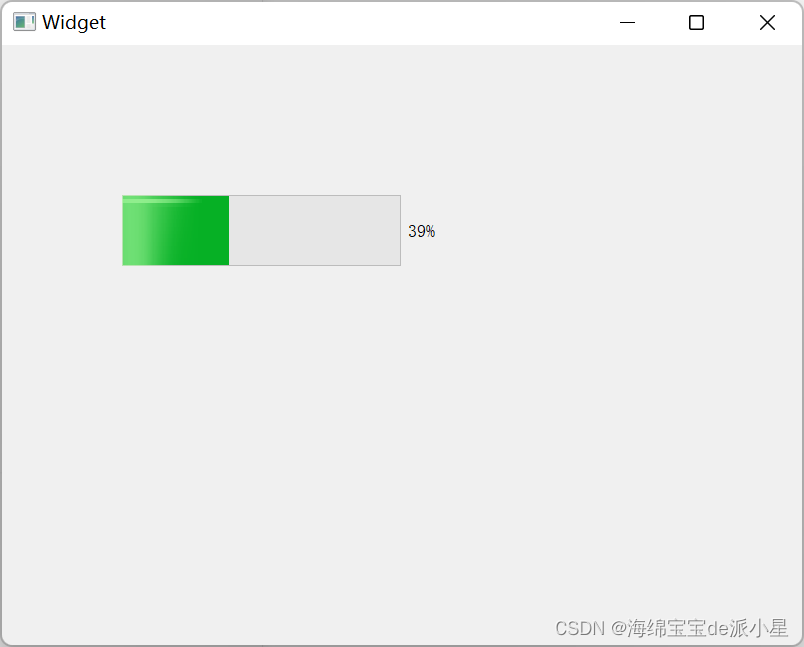
QT:label标签/进度条的使用
文章目录 设置不同格式的文本显示图片文本对齐/自动换行/缩进/边距LCDNumber倒计时 ProgressBar进度条 设置不同格式的文本 在文本格式中,存在富文本,makedown格式的文本,还有纯文本,下面就依据这三个进行举例 #include "w…...

网络初始化配置
IPADDR192.168.23.10 #新的ip地址,ip的网段要与nat模式下的网段一致 NETMASK255.255.255.0 #子网掩码 GATEWAY192.168.23.2 #网关 DNS1114.114.114.114 #域名解析:配置为国内114.114.114.114,国外8.8.8.8 ONBOOTtrue 启动时该网卡…...

在Ubuntu上搭建并通过systemctl管理Minecraft Java版服务器
本教程将详细介绍如何在Ubuntu操作系统上搭建一个Minecraft Java版服务器,并使用systemctl服务来管理服务器的启动、停止和重启。同时,我们还将探讨如何通过NGINX设置TCP/UDP转发,使得玩家能够通过域名方便地连接到你的Minecraft服务器。 准…...

【C++PCL】点云处理ESF描述符
作者:迅卓科技 简介:本人从事过多项点云项目,并且负责的项目均已得到好评! 公众号:迅卓科技,一个可以让您可以学习点云的好地方 重点:每个模块都有参数如何调试的讲解,即调试某个参数对结果的影响是什么,大家有问题可以评论哈,如果文章有错误的地方,欢迎来指出错误的…...

鸿蒙应用开发系列 篇二:鸿蒙系统开发工具与环境
文章目录 系列文章硬件与软件需求DevEco Studio扩展工具与框架开发资源系列文章 鸿蒙应用开发系列 篇一:鸿蒙系统概述 鸿蒙应用开发系列 篇二:鸿蒙系统开发工具与环境 (系列计划预告) 鸿蒙系统UI/UX设计 鸿蒙系统应用开发基础 鸿蒙系统高级开发技术 鸿蒙系统特色功能开发 …...

“A”分心得:我的云计算HCIE学习之路
大家好,我是誉天云计算HCIE周末班梁同学,在誉天老师和同学们的帮助下,我终于在4月24日顺利通过了云计算3.0 HCIE的认证考试,而且获得了A,这是让我特别惊喜的,功夫不负有心人。 我日常的工作是网络运维&…...
现代信号处理8_递归的最小二乘(CSDN_20240505)
递归的最小二乘大约出现在50年前。递归,就是在已经算出的结果的基础下,当新的数据到来时,不需要再对数据进行一次完整的运算,而是在已有结果的基础上做一些简单的调整,就能得到新的结果。使用递归的好处: …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
