【蓝桥杯集训·每日一题】AcWing 4074. 铁路与公路
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- Floyd 算法
- Spfa 算法
一、题目
1、原题链接
4074. 铁路与公路
2、题目描述
某国家有 n 个城市(编号 1∼n)和 m 条双向铁路。
每条铁路连接两个不同的城市,没有两条铁路连接同一对城市。
除了铁路以外,该国家还有公路。
对于每对不同的城市 x,y,当且仅当它们之间没有铁路时,它们之间会存在一条双向公路。
经过每条铁路或公路都需要花费 1 小时的时间。
现在有一列火车和一辆汽车同时离开城市 1,它们的目的地都是城市 n。
它们不会在途中停靠(但是可以在城市 n 停靠)。
火车只能沿铁路行驶,汽车只能沿公路行驶。
请你为它们规划行进路线,每条路线中可重复经过同一条铁路或公路,但是为了避免发生事故,火车和汽车不得同时到达同一个城市(城市 n 除外)。
请问,在这些条件的约束下,两辆车全部到达城市 n 所需的最少小时数,即求更慢到达城市 n 的那辆车所需的时间的最小值。
注意,两辆车允许但不必要同时到达城市 n。
输入格式
第一行包含整数 n 和 m。
接下来 m 行,每行包含两个整数 u,v,表示城市 u 和城市 v 之间存在一条铁路。
输出格式
一个整数,表示所需的最少小时数。
如果至少有一辆车无法到达城市 n,则输出 −1。
数据范围
前 6 个测试点满足 2≤n≤10,0≤m≤10。
所有测试点满足 2≤n≤400,0≤m≤n(n−1)/2,1≤u,v≤n。输入样例1:
4 2 1 3 3 4输出样例1:
2输入样例2:
4 6 1 2 1 3 1 4 2 3 2 4 3 4输出样例2:
-1输入样例3:
5 5 4 2 3 5 4 5 5 1 1 2输出样例3:
3
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)如果从城市1到城市n之间有铁路,则从城市1到城市n,火车会直接到达城市n,而汽车会走公路经过某些城市然后再到达城市n,所以火车和汽车必然不会在城市1~n(除城市1和城市n)中的任意一座城市停留。
(2)同理,如果从城市1到城市n之间有公路,汽车和火车也必然不会在城市1~n(除城市1和城市n)中的任意一座城市停留。
(3)综上,任何情况下火车和汽车从城市1到达城市n,如果可以到达,则在路径之中必然不会同时在1~n(除城市1和城市n)中的某一座城市停留。
(4)所以,题目中的约束条件始终无法满足,我们只需要求出火车和汽车分别到达城市n的最短时间,然后取最大者即可。
2、时间复杂度
Floyd算法时间复杂度为O(n3)
Spfa算法时间复杂度为O(nm)
3、代码详解
Floyd算法求解
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=410;
int n,m;
int f[N][N],g[N][N]; //f[i][j]存储从i城市到j城市走铁路的花费时间,如果不存在铁路则为正无穷;g[i][j]存储公路的,同理
//floyd算法求最短路
int floyd(int d[][N]){if(d[1][n]==1) return 1; //如果城市1到城市n存在一条公路/铁路,花费时间为1,直接返回即可for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){d[i][j]=min(d[i][j],d[i][k]+d[k][j]);}}}return d[1][n];
}
int main(){cin>>n>>m;memset(f,0x3f,sizeof f);memset(g,0x3f,sizeof g);while(m--){int u,v;cin>>u>>v;f[u][v]=f[v][u]=1; //无向边存两个方向}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i!=j&&f[i][j]!=1){ //如果不是自环,而且i和j之间没有铁路的话,i和j之间存在一条公路g[i][j]=1;}}}int ans=max(floyd(f),floyd(g)); //时间取两者时间的最大值if(ans==0x3f3f3f3f) cout<<-1; //如果从城市1到城市n的时间为正无穷,说明无法从城市1到达城市nelse cout<<ans;return 0;
}
Spfa算法求解
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=410,M=160010;
int h1[N],h2[N],e[M],ne[M],idx; //h1[]存储每条铁路(边),h2[]存储每条公路(边),e[]存储每条边的终点,ne[]存储每条边同起点的下一条边,idx为边的编号
bool g[N][N]; //g[i][j]存储i和j之间是否存在铁路
int n,m;
bool st[N]; //st[i]存储第i个点的最短距离是否被松弛更新过
int dist[N]; //dist[i]存储从城市1到城市i的最小花费时间
//邻接表加边
void add(int h[],int a,int b){e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
//spfa算法求最短路
int spfa(int h[],bool flag){ //flag=false表示走铁路,flag=true表示走公路//如果走铁路,而且城市1和城市n之间有铁路或者如果走公路,而且城市1和城市n之间有公路,直接返回最小时间花费1即可if(!flag&&g[1][n]||flag&&!g[1][n]) return 1;memset(dist,0x3f,sizeof dist);queue<int> q;q.push(1);st[1]=true;dist[1]=0;while(!q.empty()){int t=q.front();q.pop();st[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+1){dist[j]=dist[t]+1;if(!st[j]){st[j]=true;q.push(j);} }}}return dist[n];
}
int main(){cin>>n>>m;memset(h1,-1,sizeof h1);memset(h2,-1,sizeof h2);while(m--){int u,v;cin>>u>>v;add(h1,u,v),add(h1,v,u); //无向边,添加两次g[u][v]=g[v][u]=true; //标记u,v两点间有铁路}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(!g[i][j]){ //如果i,j之间没有铁路,则为i,j之间添加一条无向公路add(h2,i,j),add(h2,j,i);}}}int ans=max(spfa(h1,false),spfa(h2,true)); //取两者时间最大值即可if(ans==0x3f3f3f3f) cout<<-1; //如果无解,输出-1即可else cout<<ans;return 0;
}
三、知识风暴
Floyd 算法
- 基本思想:基于动态规划,首先记录两点之间无其他中间点的最短距离,然后在其中加入中间点之后,如果加入中间点之后,两点之间的最短距离更短,则更新,按上述流程,遍历完所有可能路径,算法结束。
Spfa 算法
- 参考我的这篇文章即可
相关文章:

【蓝桥杯集训·每日一题】AcWing 4074. 铁路与公路
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴Floyd 算法Spfa 算法一、题目 1、原题链接 4074. 铁路与公路 2、题目描述 某国家有 n 个城市(编号 1∼n)和 m 条双向铁路。 每条铁路连接两个不同的…...
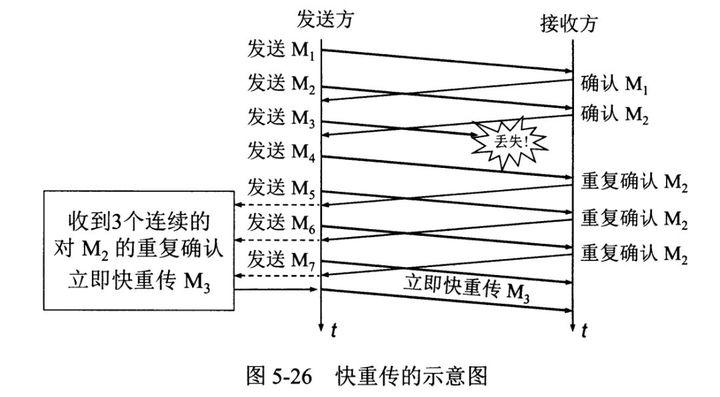
网络:TCP与UDP相关知识(详细)
目录:1、UDP 和 TCP 的特点与区别2、UDP 、TCP 首部格式3、TCP 的三次握手和四次挥手4、TCP 的三次握手(为什么三次?)5、TCP 的四次挥手(为什么四次?)6、TCP 长连接和短连接的区别7、TCP粘包、拆…...
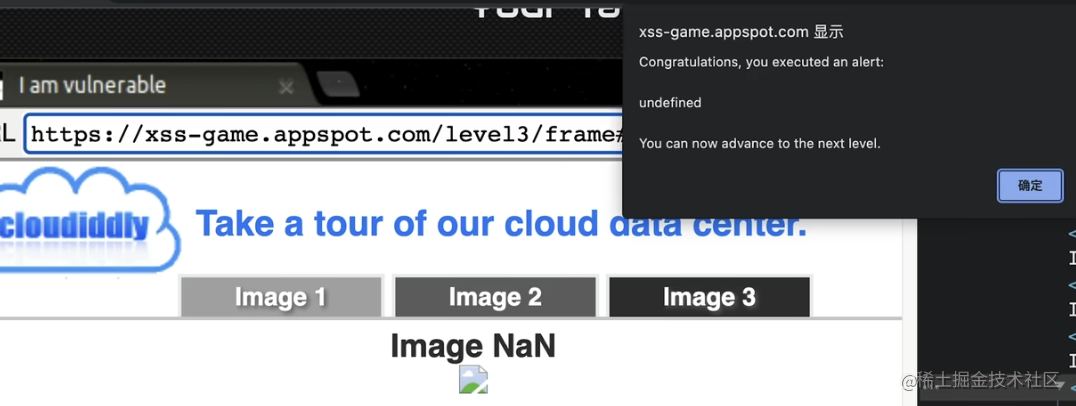
不好!有敌情,遭到XSS攻击【网络安全篇】
XSS:当一个目标的站点,被我们用户去访问,在渲染HTMl的过程中,出现了没有预期到的脚本指令,然后就会执行攻击者用各种方法注入并执行的恶意脚本,这个时候就会产生XSS。 涉及方: 用户࿰…...

Mysql中Explain详解及索引的最佳实践
Mysql中Explain详解及索引的最佳实践1.Explan工具的介绍1.1 Explan 分析示例1.2 Explain中的列1.2.1 id1.2.2 select_type1.2.3 table1.2.4 partitions1.2.5 type1.2.6 possible_keys1.2.7 key1.2.8 key_len1.2.9 ref1.2.10 rows1.2.11 filtered1.2.12 Extra1.Explan工具的介绍…...

JavaScript 内的 this 指向
在 javascript 语言中, 有一个奇奇怪怪的 “关键字” 叫做 this为什么说它是 奇奇怪怪 呢, 是因为你写出 100 个 this, 可能有 100 个解释, 完全不挨边,但是, 在你的学习过程中, 搞清楚了 this 这个玩意, 那么会对你的开发生涯有很大帮助的,接下来咱们就…...
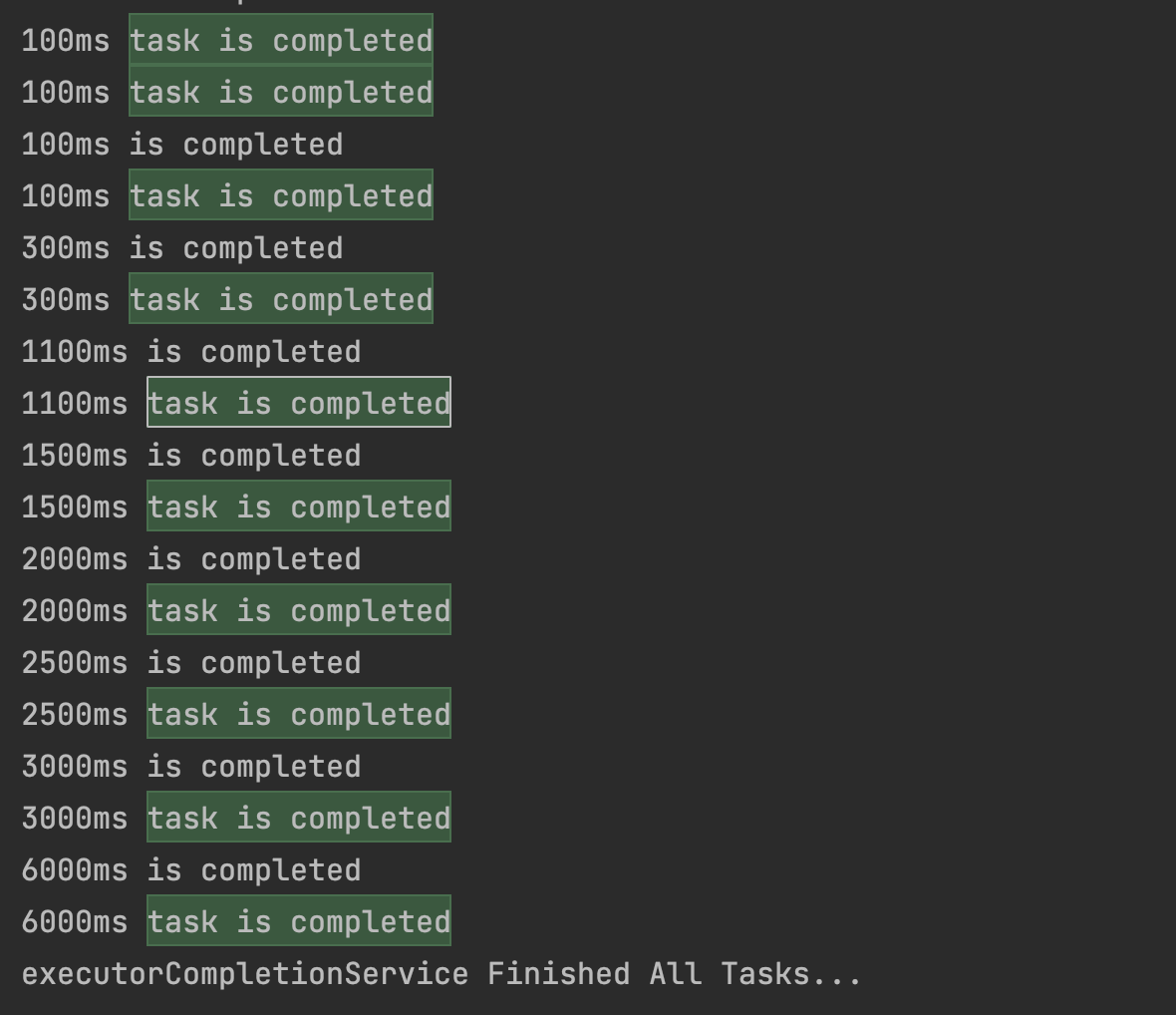
Java多种方法实现等待所有子线程完成再继续执行
简介 在现实世界中,我们常常需要等待其它任务完成,才能继续执行下一步。Java实现等待子线程完成再继续执行的方式很多。我们来一一查看一下。 Thread的join方法 该方法是Thread提供的方法,调用join()时,会阻塞主线程࿰…...

制造企业数字化工厂建设步骤的建议
随着工业4.0、中国制造2025的深度推进,越来越多的制造企业开始迈入智能制造的领域,那数字工厂要从何入手呢? 数字工厂规划的核心,也正是信息域和物理域这两个维度,那就从这两个维度来进行分析,看如何进行数…...
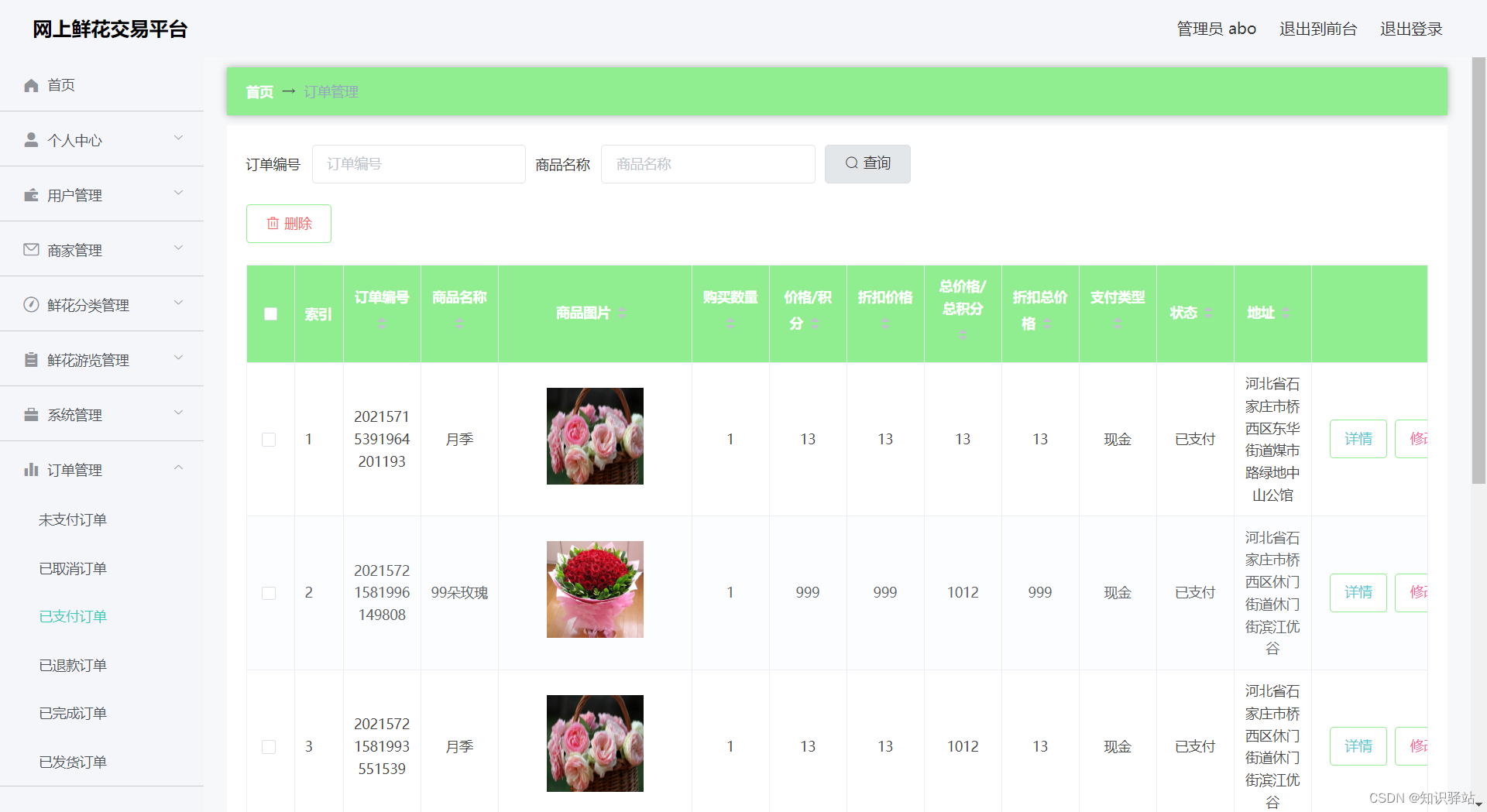
网上鲜花交易平台,可运行
文章目录项目介绍一、项目功能介绍1、用户模块主要功能包括:2、商家模块主要功能包括:3、管理员模块主要功能包括:二、部分页面展示1、用户模块部分功能页面展示2、商家模块部分功能页面展示3、管理员模块部分功能页面展示三、部分源码四、底…...

【实战】用 Custom Hook + TS泛型实现 useArray
文章目录一、题目二、答案(非标准)三、关键知识点1.Custom Hook关键点案例useMountuseDebounce2.TS 泛型关键点一、题目 完善自定义 Hook —— useArray ,使其能够完成 tryUseArray 组件中测试的功能: 入参:数组返回…...
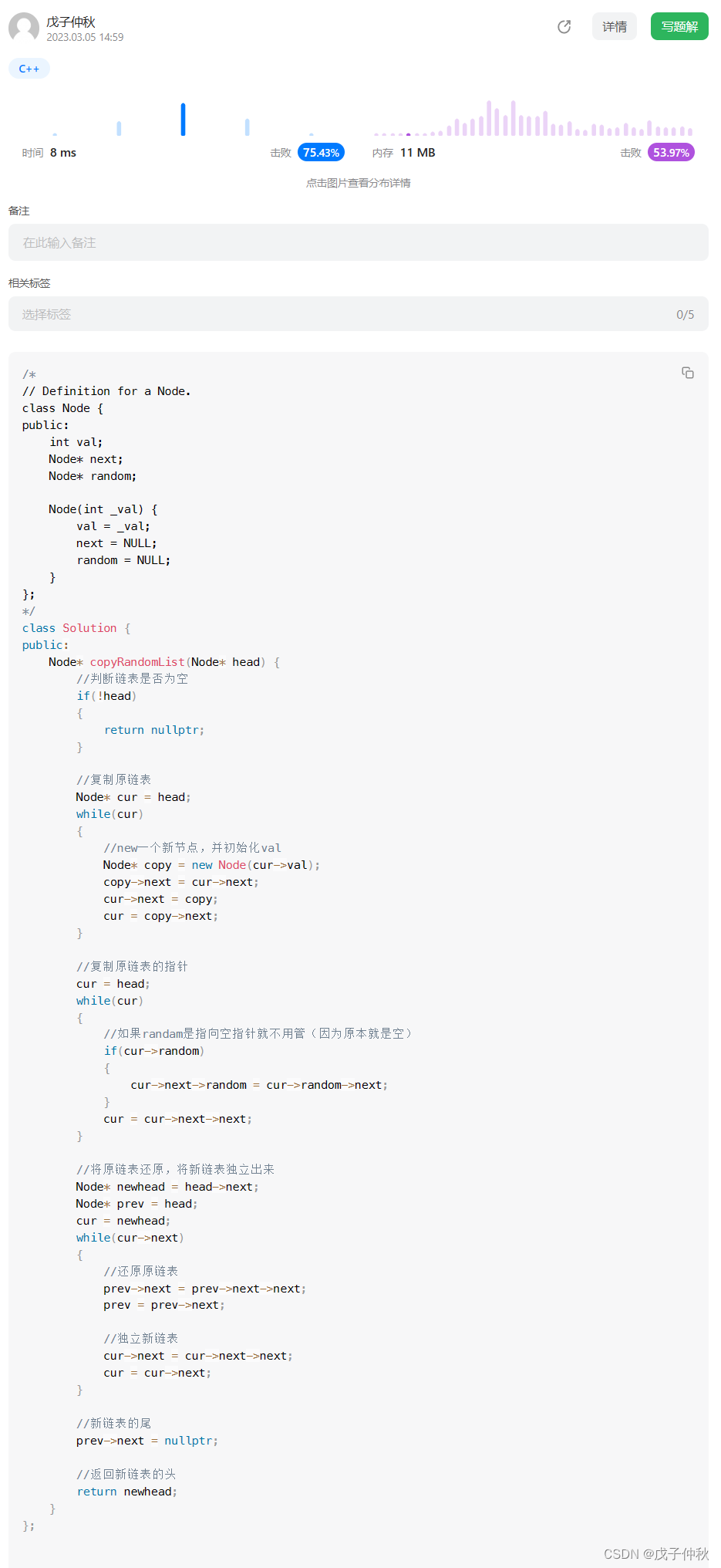
【LeetCode】剑指 Offer(18)
目录 题目:剑指 Offer 35. 复杂链表的复制 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 35. 复杂链…...

Kubernetes节点运行时从Docker切换到Containerd
由于k8s将于1.24版本弃用dockershim,所以最近在升级前把本地的k8s切换到了Containerd运行时,目前我的k8s版本是1.22.5,一个master,二个Node的配置,以下做为一个操作记录日志整理,其它可以参考官网文档。 在…...
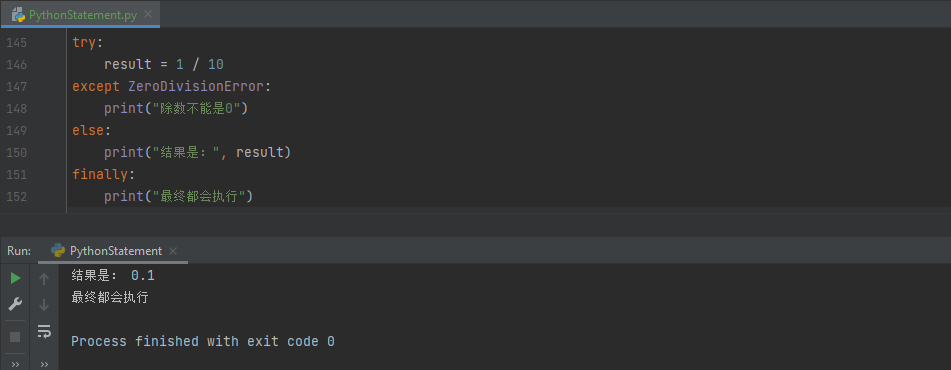
【编程基础之Python】12、Python中的语句
【编程基础之Python】12、Python中的语句Python中的语句赋值语句条件语句循环语句for循环while循环continue语句break语句continue与break的区别函数语句pass语句异常处理语句结论Python中的语句 Python是一种高级编程语言,具有简单易学的语法,适用于各…...
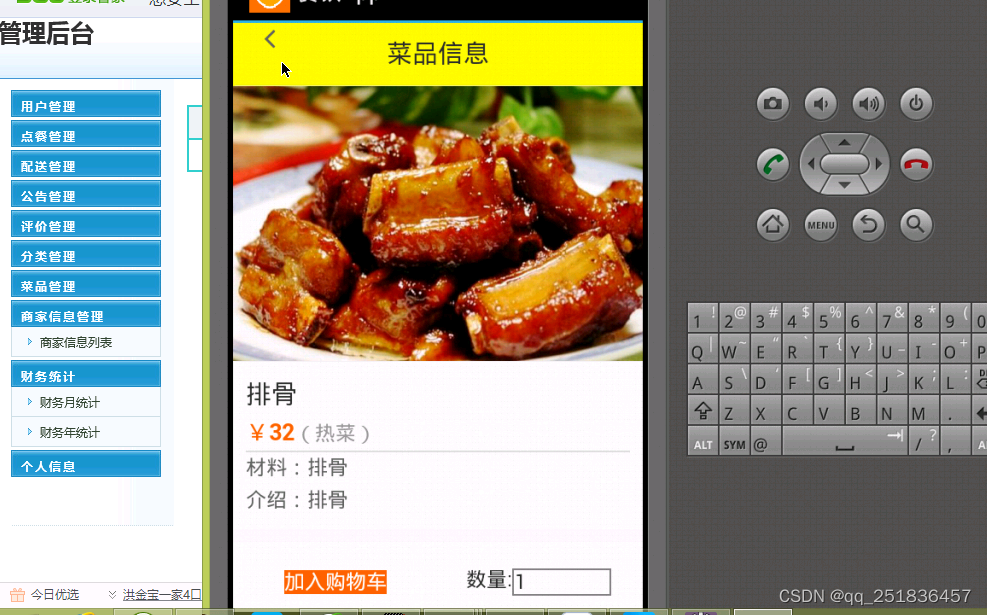
android h5餐饮管理系统myeclipse开发mysql数据库编程服务端java计算机程序设计
一、源码特点 android h5餐饮管理系统是一套完善的WEBandroid设计系统,对理解JSP java,安卓app编程开发语言有帮助(系统采用web服务端APP端 综合模式进行设计开发),系统具有完整的源代码和数据库,系统主要…...
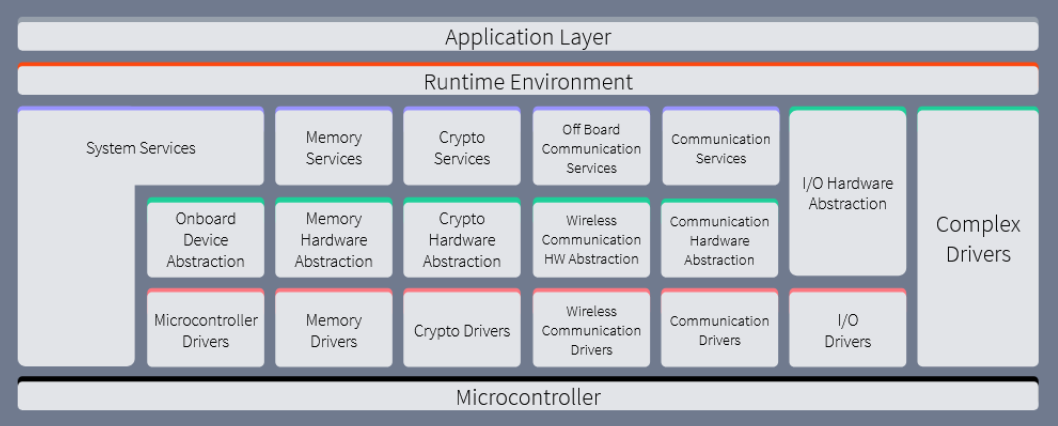
容易混淆的嵌入式(Embedded)术语
因为做嵌入式开发工作虽然跳不出电子行业,但还是能接触到跨度较大的不同行当,身处不同的圈子。诸如医疗,银行,车载,工业;亦或者手机,PC,专用芯片;甚至可能横跨系统开发、…...

Nodejs 中 JSON 和 YAML 互相转换
JSON 转换成 YAML 1. 安装 js-yaml 库: npm install js-yaml2. 在程序中引入依赖库 const yaml require(js-yaml);3. 创建一个 js 对象, 代表 json 数据 const jsonData {name: John,age: 30,city: New York };4. 使用 yaml.dump() 把 js 对象转换成 YAML, 返回 YAML 字符…...

C++入门教程||C++ 修饰符类型||C++ 存储类
C 修饰符类型 C 允许在 char、int 和 double 数据类型前放置修饰符。修饰符用于改变基本类型的含义,所以它更能满足各种情境的需求。 下面列出了数据类型修饰符: signedunsignedlongshort 修饰符 signed、unsigned、long 和 short 可应用于整型&#…...

Android开发面试:Java知识答案精解
目录 Java 集合 集合概述 HashMap ConcurrentHashMap 泛型 反射 注解 IO流 异常、深浅拷贝与Java8新特性 Java异常 深浅拷贝 Java8新特性 并发 线程 线程池 锁 volatile JVM 内存区域 内存模型 类加载机制 垃圾回收机制 如何判断对象已死 Java 集合 …...
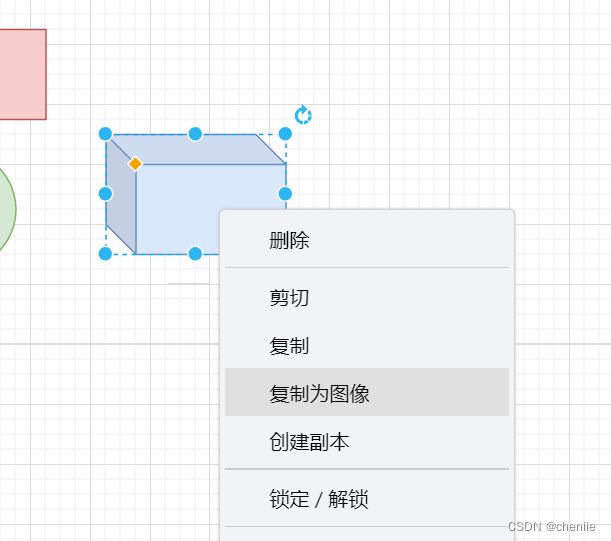
Windows上一款特别好用的画图软件
安装 废话不多说,打开windows的应用商店,搜索draw.io,点击获取即可。 画图 draw.io的布局左边是各种图形组件,中间是画布,右边是属性设置,文件扩展名是.drawio。 点击左边列表中的图形可以将它添加到画…...

html--学习
javascrapt交互,网页控制JavaScript:改变 HTML 图像本例会动态地改变 HTML <image> 的来源(src):点亮灯泡<script>function changeImage() {elementdocument.getElementById(myimage) #内存变量࿰…...
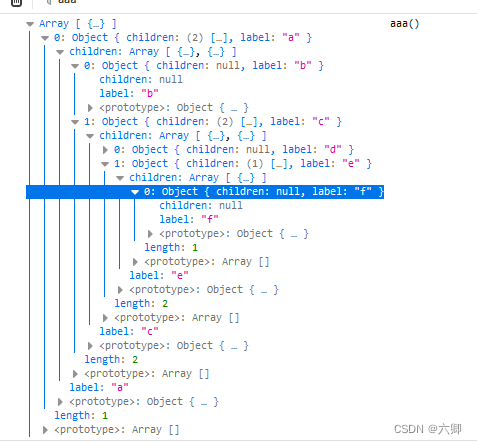
关于递归处理,应该怎么处理,思路是什么?
其实问题很简单,就是想要循环遍历整个data对象,来实现所有name转成label,但是想到里面还有children属性,整个children里面可能还会嵌套很多很多的name,如此循环,很难搞,知道使用递归,…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
